Свойство 1 Если две параллельные плоскости

Свойство 1 Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны

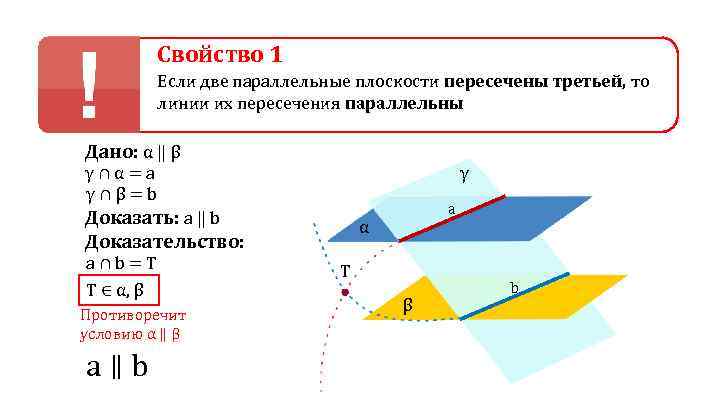Свойство 1 Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны Дано: α ‖ β γ∩α=a γ γ∩β=b a Доказать: a ‖ b α Доказательство: a∩b=T T T ∈ α, β b Противоречит β условию α ‖ β a ∥ b

Свойство 2 Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны

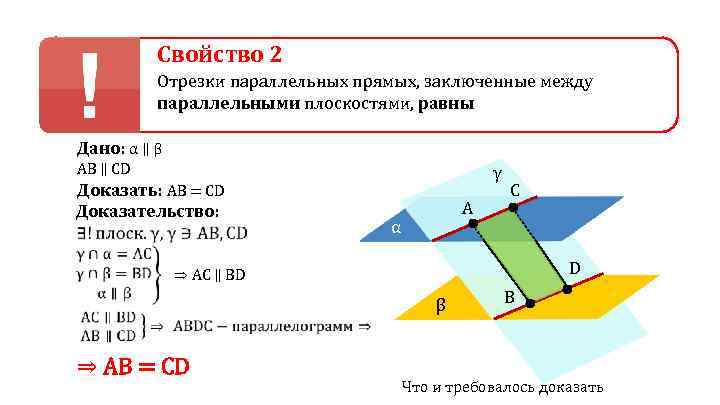Свойство 2 Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны Дано: α ∥ β AB ∥ CD γ Доказать: AB = CD C Доказательство: A α ⇒ АС ∥ BD β B ⇒ AB = CD Что и требовалось доказать

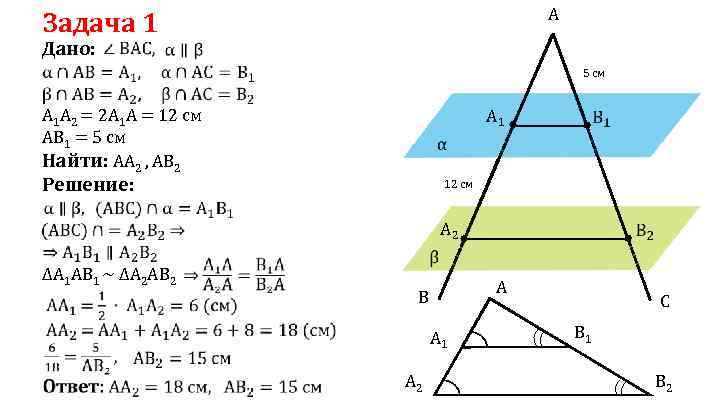A Задача 1 Дано: 5 см A 1 A 2 = 2 A 1 A = 12 см A 1 AB 1 = 5 см Найти: АА 2 , АВ 2 Решение: 12 см A 2 ∆А 1 АВ 1 ∼ ∆А 2 АВ 2 А B C А 1 В 1 А 2 B 2