СВОЙСТВА ФУНКЦИИ У SIN X И y

СВОЙСТВА ФУНКЦИИ У = SIN X И y ЕЕ ГРАФИК - 2π -π 0 Автор Попова Л. А. π 2π x 1

Свойства функции • • • 1. D(y) 2. E(y) 3. Четность функции 4. Периодичность функции 5. Нули функции 6. Наибольшее значение 7. Наименьшее значение 8. Положительные значения 9. Отрицательные значения 10. Возрастание функции 11. Убывание функции 2

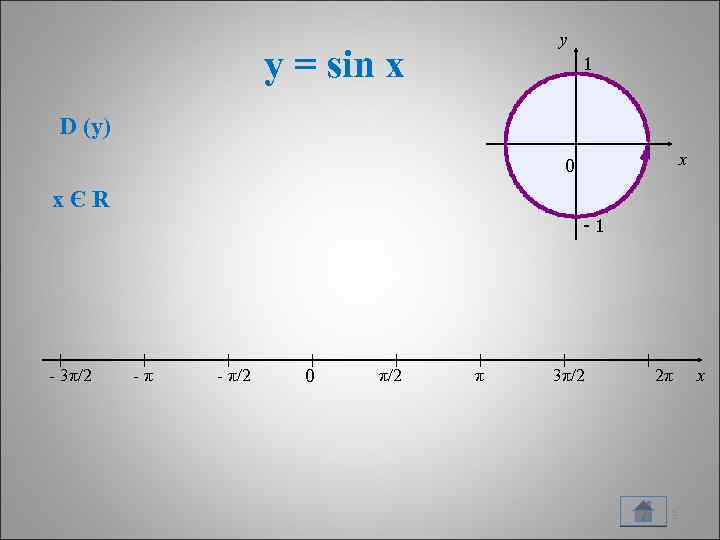y y = sin x 1 D (y) x 0 xЄR -1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π 3 x

y y = sin x E (y) 1 [ -1; 1] 0 y x -1 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π -1 4 x

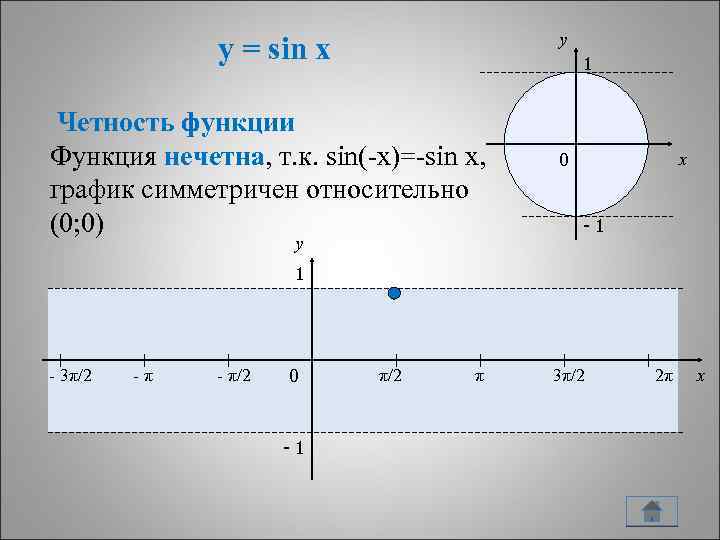y y = sin x 1 Четность функции Функция нечетна, т. к. sin(-x)=-sin x, график симметричен относительно (0; 0) y 0 x -1 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π -1 5 x

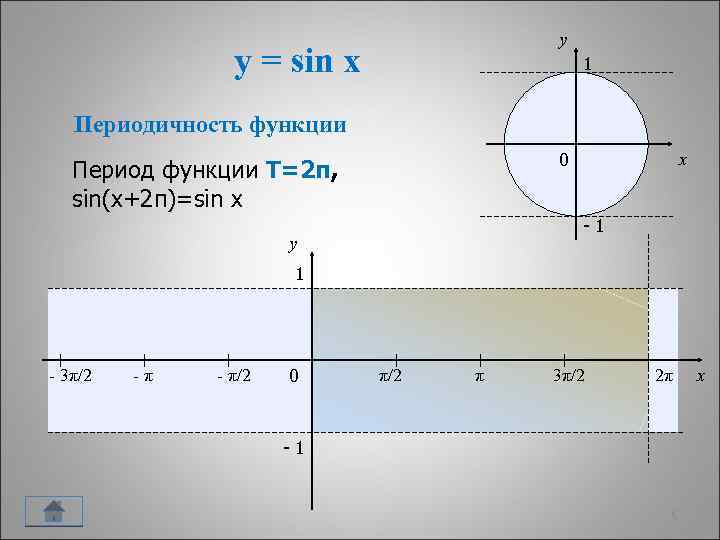y y = sin x 1 Периодичность функции 0 Период функции Т=2π, sin(x+2π)=sin x x -1 y 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π -1 6 x

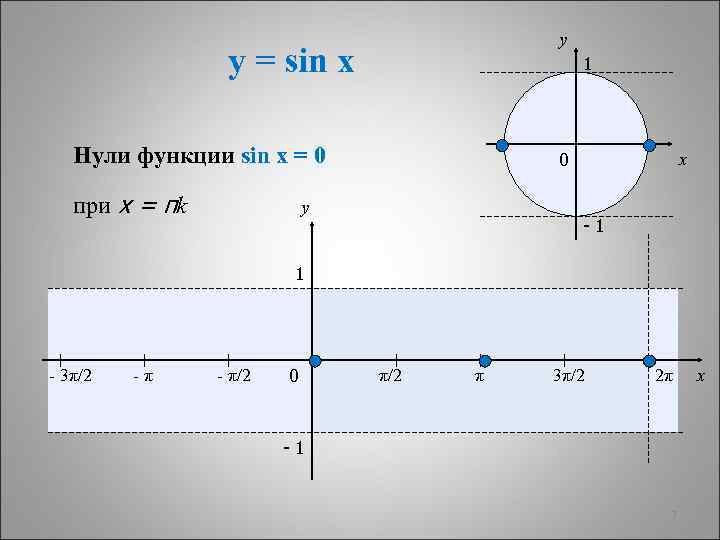y y = sin x 1 Нули функции sin x = 0 при x = πk 0 y x -1 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π -1 7 x

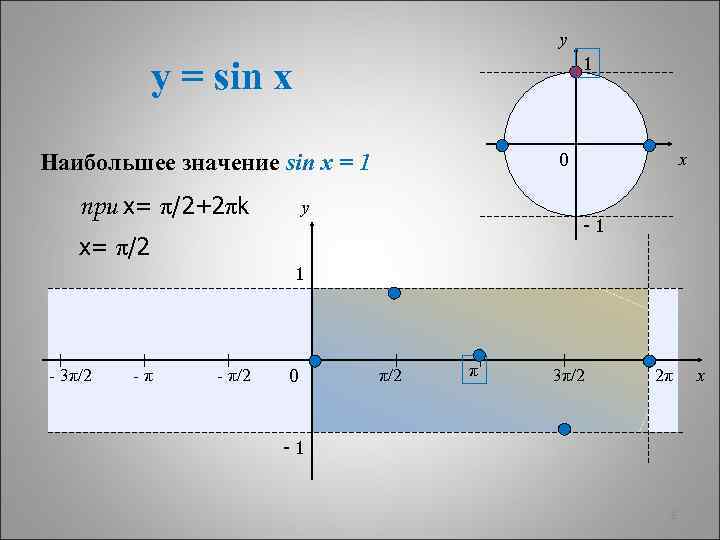y 1 y = sin x 0 Наибольшее значение sin x = 1 при х= π/2+2πk y x -1 х= π/2 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π -1 8 x

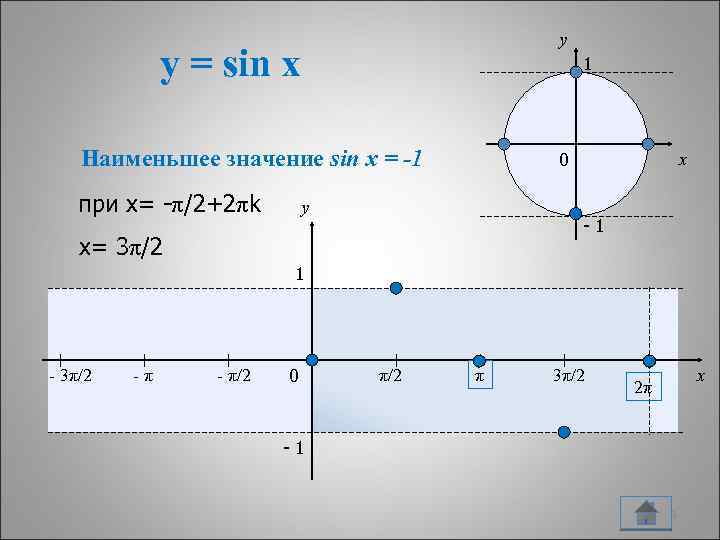y y = sin x 1 Наименьшее значение sin x = -1 при х= -π/2+2πk 0 y x -1 х= 3π/2 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 x 2π -1 9

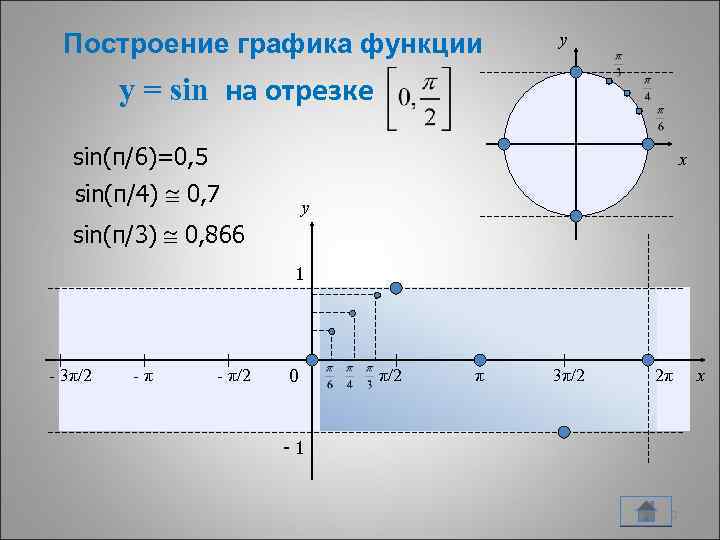Построение графика функции y y = sin на отрезке sin(π/6)=0, 5 x sin(π/4) 0, 7 y sin(π/3) 0, 866 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π -1 10 x

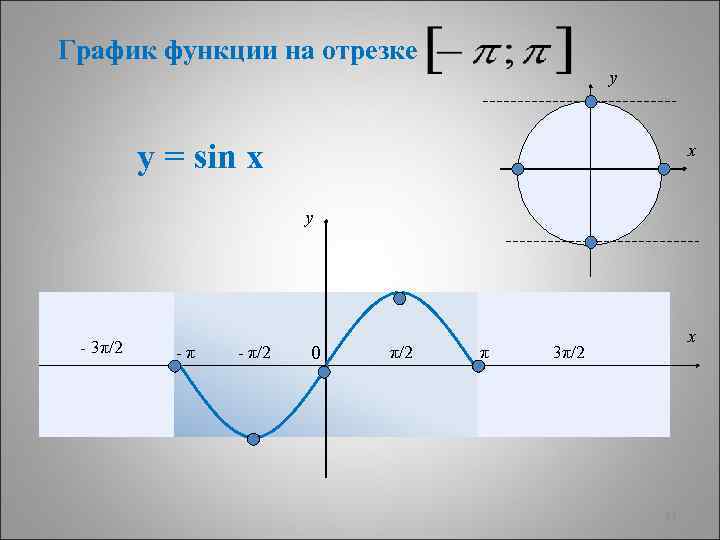График функции на отрезке y у = sin x x y - 3π/2 -π - π/2 0 π/2 π x 3π/2 11

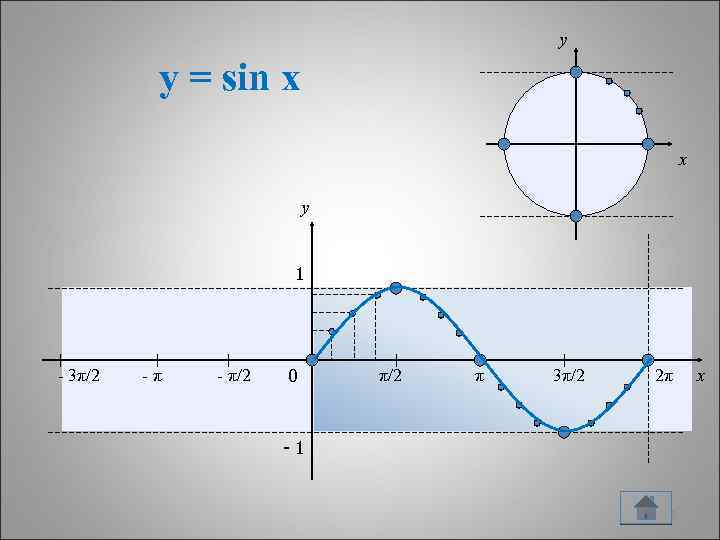y y = sin x x y 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π -1 12 x

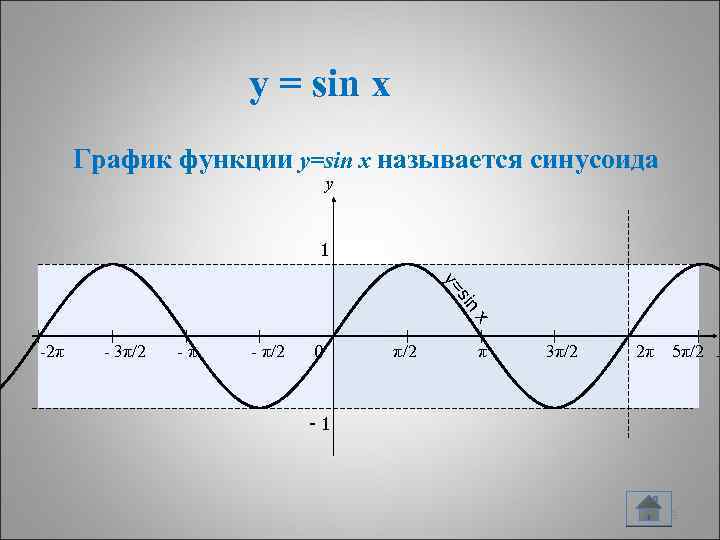y = sin x График функции y=sin x называется синусоида y 1 in s y= x -2π - 3π/2 -π - π/2 0 π/2 π 3π/2 2π 5π/2 x -1 13

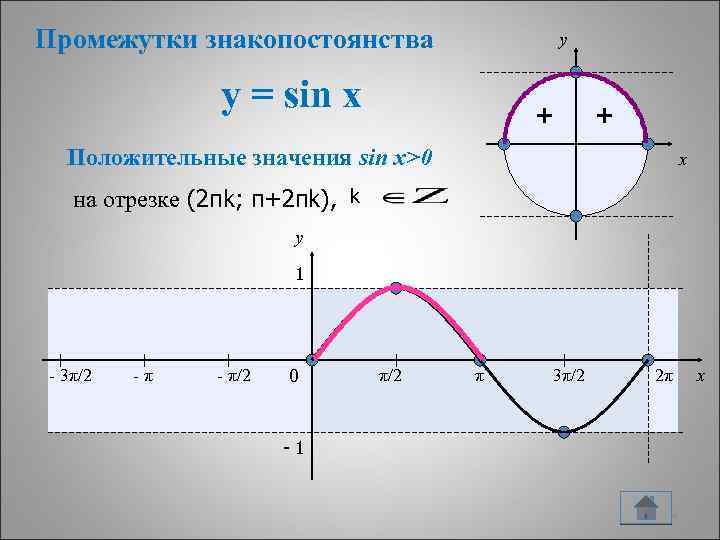Промежутки знакопостоянства y y = sin x + + Положительные значения sin x>0 x на отрезке (2πk; π+2πk), k y 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π -1 14 x

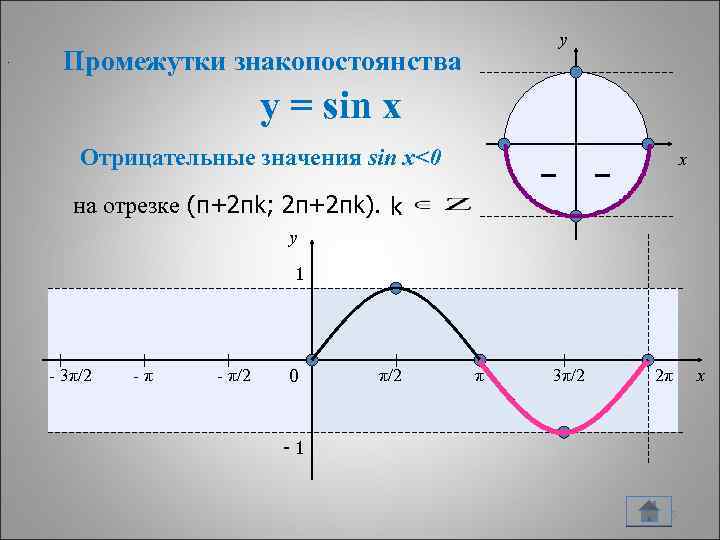. y Промежутки знакопостоянства y = sin x Отрицательные значения sin x<0 – x – на отрезке (π+2πk; 2π+2πk). k y 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π -1 15 x

Промежутки возрастания y y = sin x Функция возрастает на отрезке [-π/2+2πk; π/2+2πk] x y 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 x 2π -1 16

Промежутки убывания y y = sin x x Функция убывает на отрезке [π/2+2πk; 3π/2+2πk] y 1 - 3π/2 -π - π/2 0 π/2 π 3π/2 2π -1 17 x

Задача Сравнить числа Так как sin 2 и = 3, 14, sin 3 , то < 2 < 3 < Из графика видно, что на отрезке функция у=sinх убывает. Ответ: sin 2 > sin 3. 18

Упражнения Пользуясь свойствами функции у = sin x , сравните числа: sin 1000 sin 4 и sin 1300 и sin 2 и

Расположить в порядке возрастания числа sin 1. 9 ; sin 3; sin(-1); sin(-1. 5). Числа sin 1. 9 и sin 3 положительны, так как точки Р 1, 9 и Р 3 находятся во 2 четверти. Функция у=sinх во 2 четверти убывает. sin 3 < sin 1. 9 Числа sin(-1) и sin(-1. 5) отрицательны, так как точка Р(-1) и Р(-1, 5) находятся в 4 четверти. Функция у=sinх во 4 четверти возрастает. . sin(-1. 5) < sin(-1. 5) Ответ: Таким образом, в порядке возрастания эти чила располагаются так: sin(-1. 5); sin(-1); sin 3; sin 1. 9.

Используя свойство возрастания или убывания функции y=sinx, сравните числа: 1 вариант 2 вариант и и

Разбить отрезок на два так, чтобы на одном из них функция у=sin х убывала, а на другом возрастала. Ответ; На отрезке а на отрезке функция у=sin х убывает, функция возрастает. 22

№ 722 Разбить данный отрезок на два отрезка так, чтобы на одном из них функция у=sinх возрастала, а на другом убывала. - Функция возрастает 1) - Функция убывает 2) - Функция убывает - Функция возрастает 3) - Функция убывает - Функция возрастает

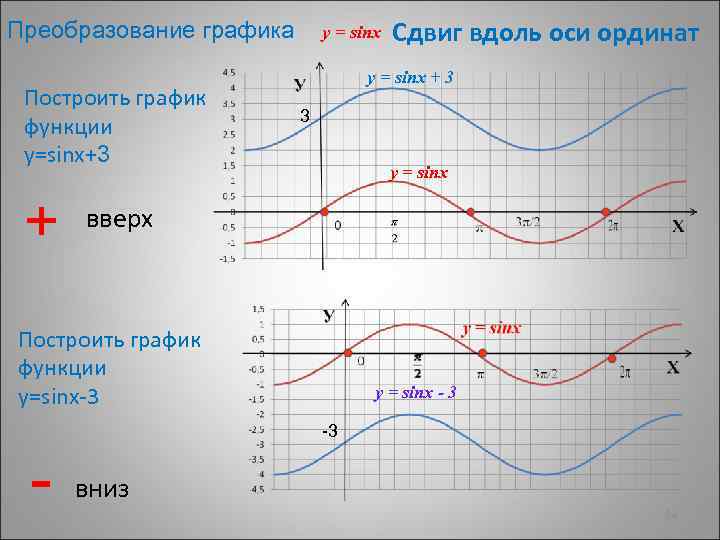Преобразование графика Построить график функции у=sinх+3 + y = sinx Сдвиг вдоль оси ординат y = sinx + 3 3 y = sinx вверх Построить график функции у=sinх-3 y = sinx - 3 -3 - вниз 24

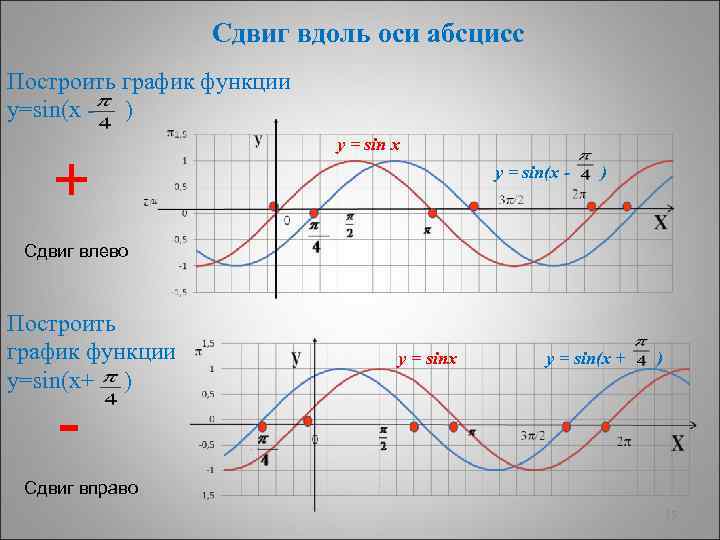Сдвиг вдоль оси абсцисс Построить график функции у=sin(х - ) + y = sin x y = sin(x - ) Сдвиг влево Построить график функции у=sin(х+ ) y = sinx y = sin(x + ) - Сдвиг вправо 25

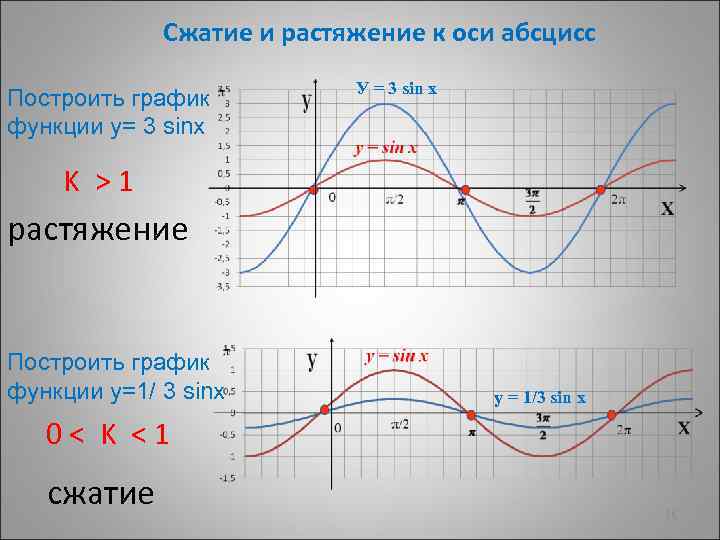Сжатие и растяжение к оси абсцисс Построить график функции у= 3 sinх У = 3 sin x K >1 растяжение Построить график функции у=1/ 3 sinх у = 1/3 sin x 0< K <1 сжатие 26

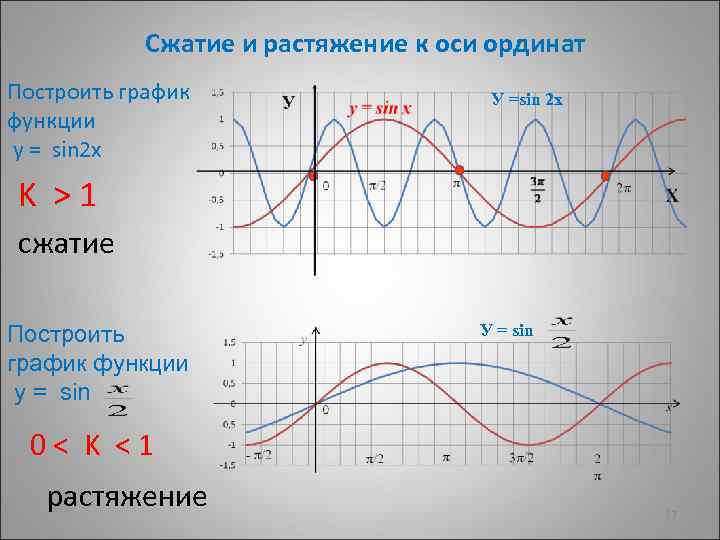Сжатие и растяжение к оси ординат Построить график функции у = sin 2 х У =sin 2 х K >1 сжатие Построить график функции у = sin У = sin 0< K <1 растяжение 27

У y = sin x х §При каких значениях х функция у=sinx принимает значение, равное 0? 1? -1? §Может ли функция у=sinx принимать значение больше 1, меньше -1? §При каких значениях х функция у=sinx принимает наибольшее (наименьшее) значение? §Каково множество значений функции у=sinx? 28