СВ ОЙ СТ ВА РА С ПР ЕД ЕЛ ЕН ИЙ
АСИММЕТРИЯ Распределение с положительной (М>Mo) асимметрией Распределение с отрицательной (M
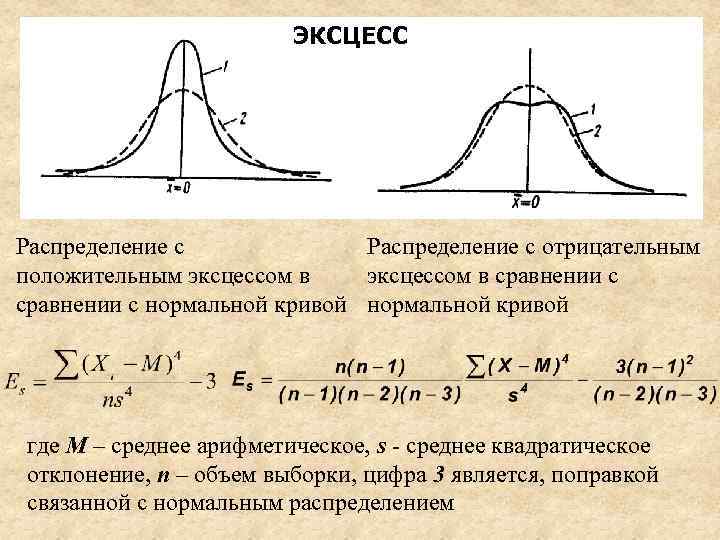ЭКСЦЕСС Распределение с отрицательным положительным эксцессом в сравнении с нормальной кривой где М – среднее арифметическое, s - среднее квадратическое отклонение, n – объем выборки, цифра 3 является, поправкой связанной с нормальным распределением
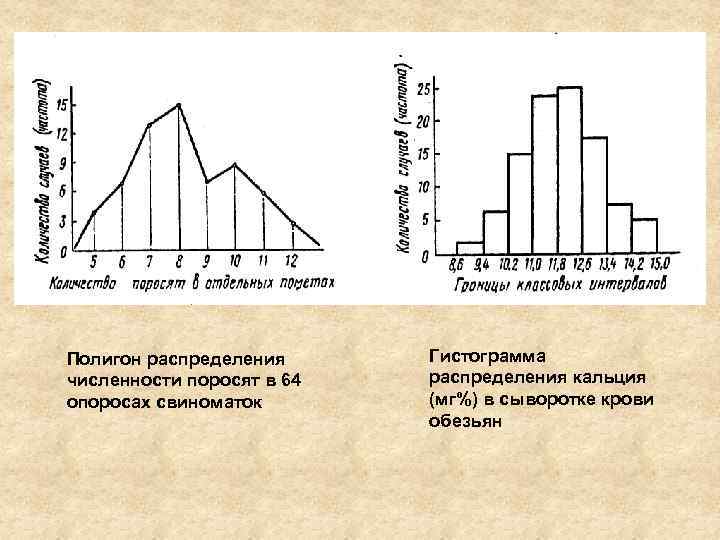Полигон распределения численности поросят в 64 опоросах свиноматок Гистограмма распределения кальция (мг%) в сыворотке крови обезьян
БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Возникает в тех случаях, когда ставится вопрос: сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях. Будем полагать, что нам известна величина p – вероятность того, что вошедший в магазин посетитель окажется покупателем и (1– p) = q – вероятность того, что вошедший в магазин посетитель не окажется покупателем. Если X – число покупателей из общего числа n посетителей, то вероятность того, что среди n посетителей оказалось k покупателей равна: P(X= k)= Биномиальный коэффициент: , где k=0, 1, …n
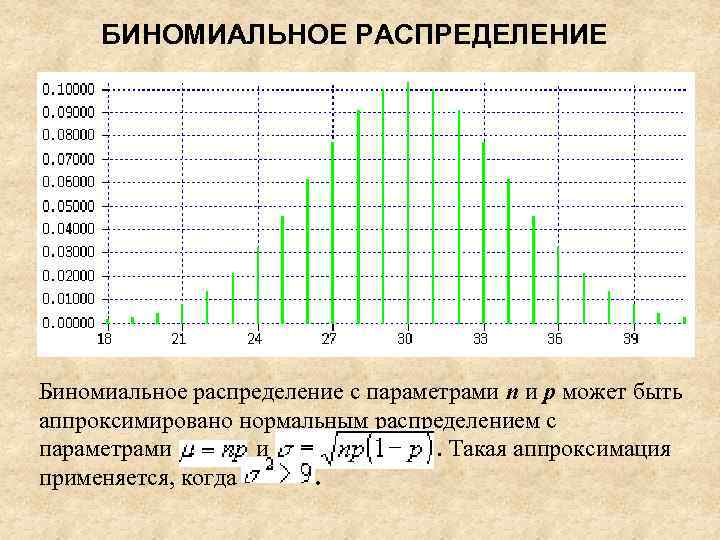БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Биномиальное распределение с параметрами n и p может быть аппроксимировано нормальным распределением с параметрами и. Такая аппроксимация применяется, когда.
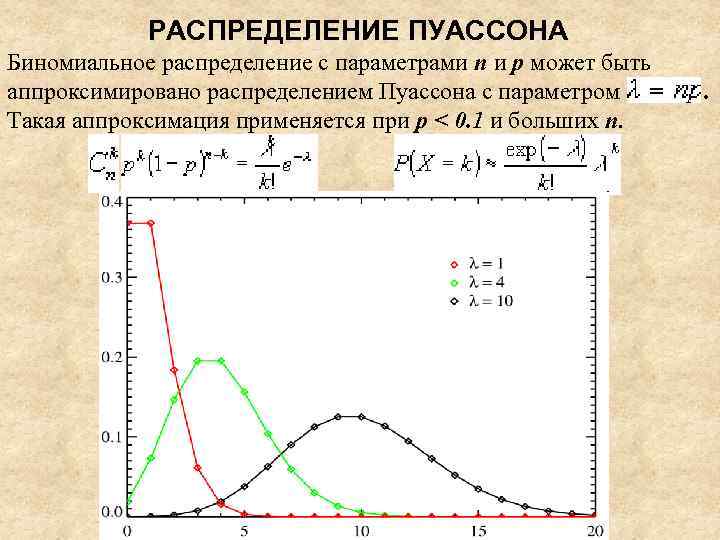РАСПРЕДЕЛЕНИЕ ПУАССОНА Биномиальное распределение с параметрами n и p может быть аппроксимировано распределением Пуассона с параметром Такая аппроксимация применяется при p < 0. 1 и больших n. .
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА Распределение по скоростям (или импульсам) молекул системы, находящейся в состоянии термодинамического равновесия.
СО П ОС ТА ВЛ ЕН ИЕ ДА НН Ы Х
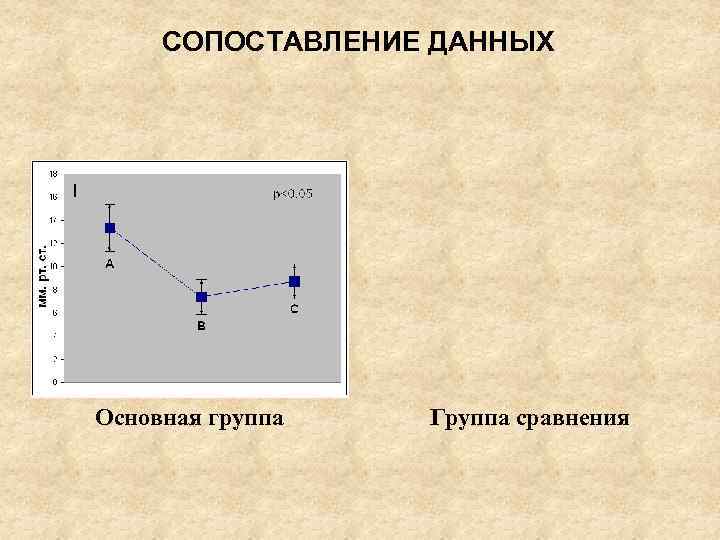СОПОСТАВЛЕНИЕ ДАННЫХ Основная группа Группа сравнения
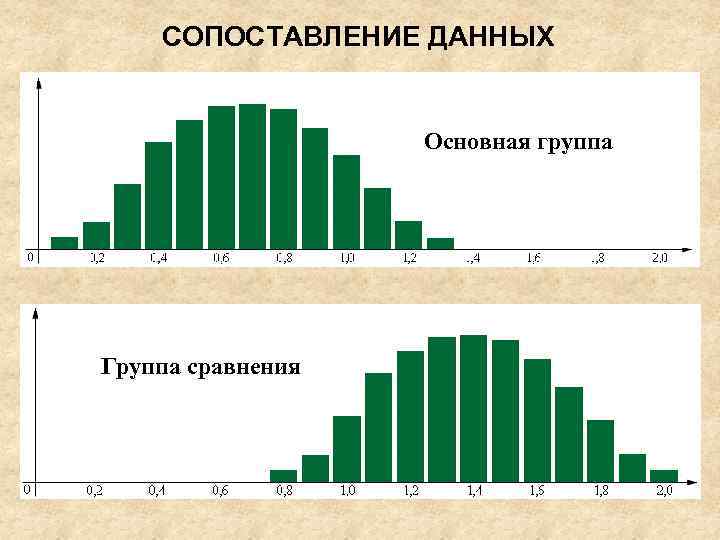СОПОСТАВЛЕНИЕ ДАННЫХ Основная группа Группа сравнения
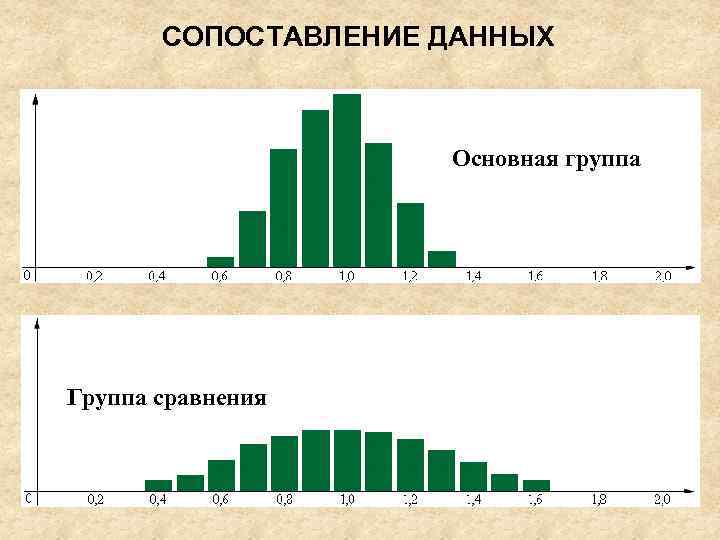СОПОСТАВЛЕНИЕ ДАННЫХ Основная группа Группа сравнения
ВЕРОЯТНОСТНЫЙ АНАЛИЗ РЕЗУЛЬТАТОВ Необходимо проанализировать вероятность того, что числовой материал предложенных выборок является/не является результатом одного и того же процесса в природе. КАК ЭТО СДЕЛАТЬ? ? Определение: Статистическим критерием называют алгоритм сопоставления выборок на предмет возможности их совпадения.
ОСНОВНЫЕ СВОЙСТВА КРИТЕРИЕВ 1. При сопоставлении выборок, все критерии возвращают значение вероятности их сходства. То есть, это вероятность события: «числовой материал предложенных выборок порожден одним и тем же процессом в природе» . 2. Чем больше сходство выборок, тем выше значение вероятности. При полном совпадении, p = 1. 3. Чем больше различие данных по выборкам, тем ниже значение вероятности. При сильных отличиях, p → 0.
ТИПЫ КРИТЕРИЕВ • Параметрические критерии предполагают, что выборка порождена нормальным распределением. Преимущество этих критериев в том, что они более мощные. Если выборка удовлетворяет дополнительным предположениям, то параметрические критерии дают более точные результаты. • Гипотезы о виде распределения проверяются с помощью критериев согласия. • Непараметрические критерии не опираются на дополнительные предположения о распределении. В частности, к этому типу критериев относится большинство ранговых критериев.
ЛИТЕРАТУРА http: //shpargalka. kiam 1. rssi. ru/statis. ru/doc/binom 2. html http: //www. genfunc. ru/theory/pril 02/ http: //stratum. ac. ru/textbooks/modelir/lection 27. html