Сущность и этапы планирования эксперимента Сущность планирования

Сущность и этапы планирования эксперимента

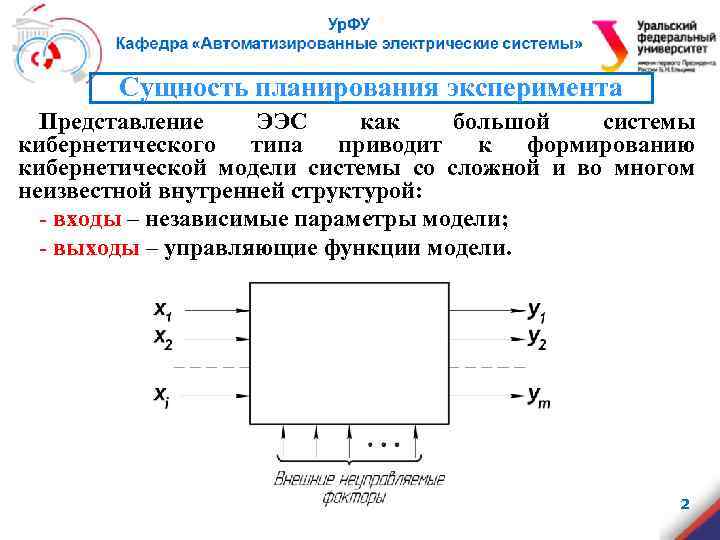Сущность планирования эксперимента Представление ЭЭС как большой системы кибернетического типа приводит к формированию кибернетической модели системы со сложной и во многом неизвестной внутренней структурой: - входы – независимые параметры модели; - выходы – управляющие функции модели. 2

Сущность планирования эксперимента Теория планирования эксперимента (ТПЭ) – изучает способы получения аналитической модели системы: – независимые параметры – факторы эксперимента ; – выходные параметры – отклик. Факторное пространство – пространство, в котором определены значения факторов и отклика. Виды эксперимента: – пассивный – сбор информации о факторах эксперимента и отклике без вмешательства в функционирование объекта; – активный – направленное изменение факторов эксперимента и отклика с целью снижения влияния на объект случайных факторов. 3

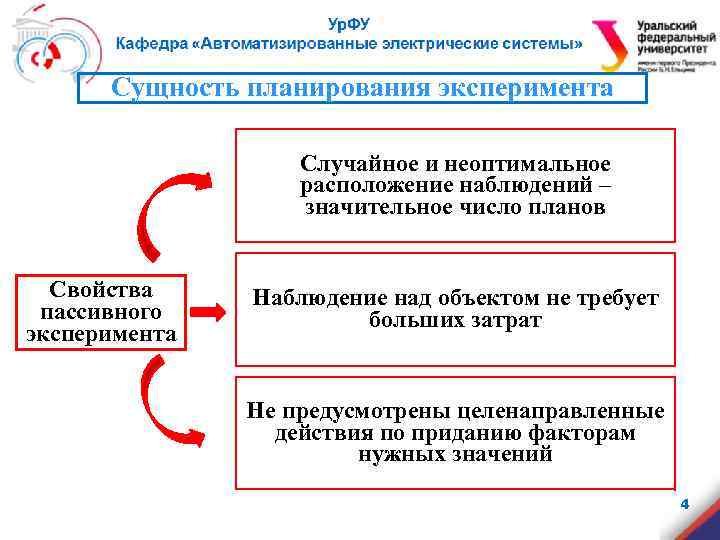Сущность планирования эксперимента Случайное и неоптимальное расположение наблюдений – значительное число планов Свойства пассивного эксперимента Наблюдение над объектом не требует больших затрат Не предусмотрены целенаправленные действия по приданию факторам нужных значений 4

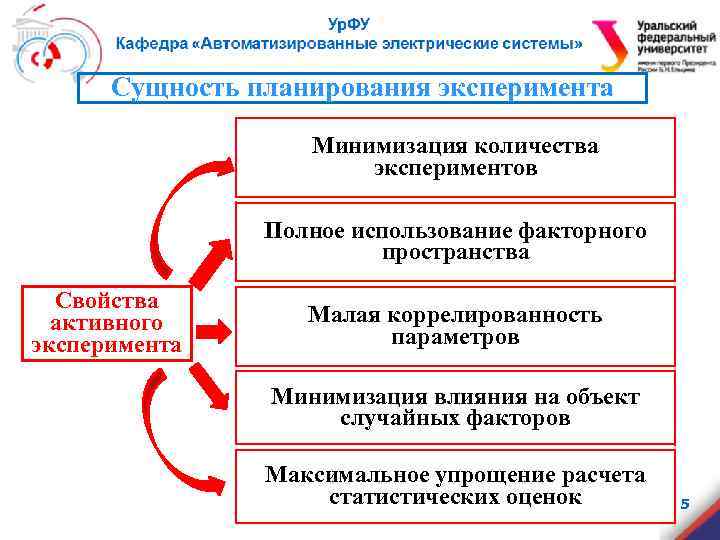Сущность планирования эксперимента Минимизация количества экспериментов Полное использование факторного пространства Свойства активного эксперимента Малая коррелированность параметров Минимизация влияния на объект случайных факторов Максимальное упрощение расчета статистических оценок 5

Сущность планирования эксперимента Этапы активного эксперимента I. Формулировка цели эксперимента и выдвижение гипотез Обычно гипотеза о составе влияющих факторов и формы связи отклика с факторами выдвигается на основе пассивного эксперимента. При выборе вида модели следует стремиться к получению возможно более простых моделей. Введение нелинейности следует использовать в том случае, когда линейная модель оказывается неадекватной или если введение нелинейного члена обусловлено его существенным влиянием на моделируемый процесс. II. Определение методики эксперимента Выбор объекта (модели) и учет ресурсов для проведения эксперимента. Выбор методики эксперимента зависит от вида объекта или модели и трудоемкости проведения опытов. III. Установление пределов варьирования факторов Диапазоны варьирования факторов эксперимента определяются при анализе внешних условий функционирования объекта, для которого намечается использование модели. При факторном эксперименте обычно рассматривают граничные значения параметров, принадлежащие крайним уровням их варьирования в данном эксперименте. При таком варьировании обследуемая зона факторного пространства представляет собой 6 многомерный параллелепипед (гиперпараллелепипед).

Сущность планирования эксперимента Предварительно целесообразно выполнить масштабирование факторов эксперимента. центрирование и Безразмерные факторы Теперь новое кодированное факторное пространство ограничено гиперкубом с координатами вершин. IV. Формирование план-матрицы эксперимента План-матрица - набор планов эксперимента , точек в факторном пространстве, соответствующих опытам. В активном эксперименте имеются возможности спланировать эксперимент и получить информационную матрицу диагонального вида. Элементы обратной матрицы диагонального вида — это величины обратные диагональным элементам матрицы. Условие построения диагональной информационной матрицы Условие ортогональности планов 7

Сущность планирования эксперимента V. Определение повторяемости опытов На отклик действуют внешние случайные неуправляемые факторы, поэтому связь отклика с входными факторами является статистической. Повторение опытов при одном сочетании факторов дает различные значения отклика. Значения отклика различаются не только между планами эксперимента, но и между конкретными реализациями в пределах каждого плана. Выполнение дублирующих экспериментов позволяет определить ошибку воспроизводимости отклика. Мера ошибки - дисперсия воспроизводимости VI. Установление порядка проведения опытов Порядок опытов имеет значение при эксперименте над объектом и не имеет значения при эксперименте над его математической моделью. VII. Проведение эксперимента и обработка его результатов 8

Полный и дробный эксперименты. Построение план-матриц эксперимента

Полный и дробный эксперименты Основная задача планирования эксперимента Расположение наблюдений в факторном пространстве так, чтобы получить информационную матрицу с заданными свойствами Эксперимент с двухуровневыми планами Цель эксперимента - установление линейной связи между откликом и факторами эксперимента x 1 u , x 2 u в виде Нормированные факторы эксперимента варьируются на двух уровнях Факторное пространство – квадрат, вершины квадрата - планы, координаты вершин квадрата - . Число планов полного факторного эксперимента (ПФК) . 10

Полный и дробный эксперименты План – матрица полного факторного эксперимента Номер плана Факторы эксперимента Отклик u x 0 u x 1 u x 2 u x 1 ux 2 u yu 1 + – – + 2 + + – - 3 + – + - 4 + + Сумма столбца 4 0 0 0 Код суммы (00) (10) (20) (12) Код строк y 1 y 2 y 3 y 4 (1) a b ab 11

Полный и дробный эксперименты Общий вид линейной модели отклика: Независимое определение коэффициентов модели отклика : В рамках эксперимента 22 можно учесть нелинейность без увеличения числа планов (коэффициенты модели определяются однозначно если число членов модели не больше числа планов): Коэффициенты неполных квадратичных моделей: 1 2

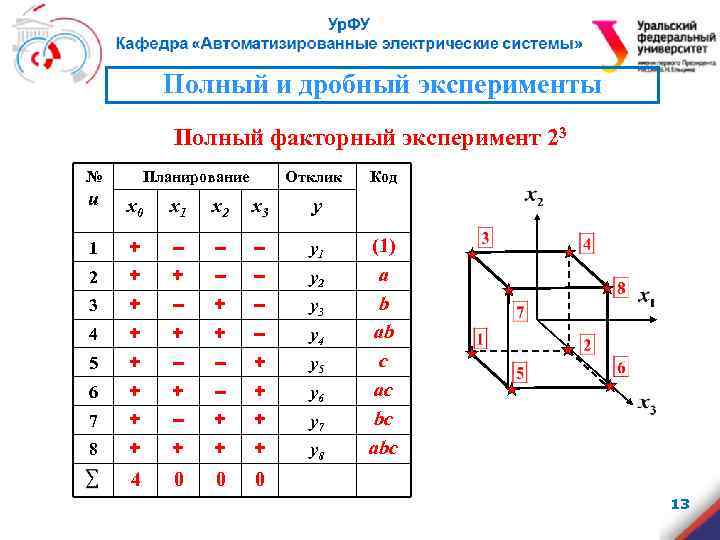Полный и дробный эксперименты Полный факторный эксперимент 23 № Планирование Отклик u x 0 x 1 x 2 x 3 y 1 + – – – y 1 2 + + – – y 2 3 + – y 3 4 + + + – y 4 5 + – – + y 5 6 + + – + y 6 7 + – + + y 7 8 + + y 8 4 0 0 Код 0 (1) a b ab с aс bс abс 13

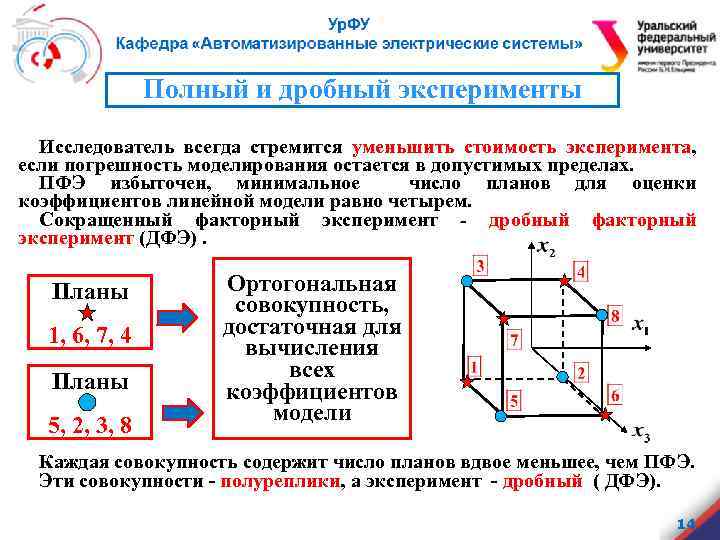Полный и дробный эксперименты Исследователь всегда стремится уменьшить стоимость эксперимента, если погрешность моделирования остается в допустимых пределах. ПФЭ избыточен, минимальное число планов для оценки коэффициентов линейной модели равно четырем. Сокращенный факторный эксперимент - дробный факторный эксперимент (ДФЭ). Планы 1, 6, 7, 4 Планы 5, 2, 3, 8 Ортогональная совокупность, достаточная для вычисления всех коэффициентов модели Каждая совокупность содержит число планов вдвое меньшее, чем ПФЭ. Эти совокупности - полуреплики, а эксперимент - дробный ( ДФЭ). 14

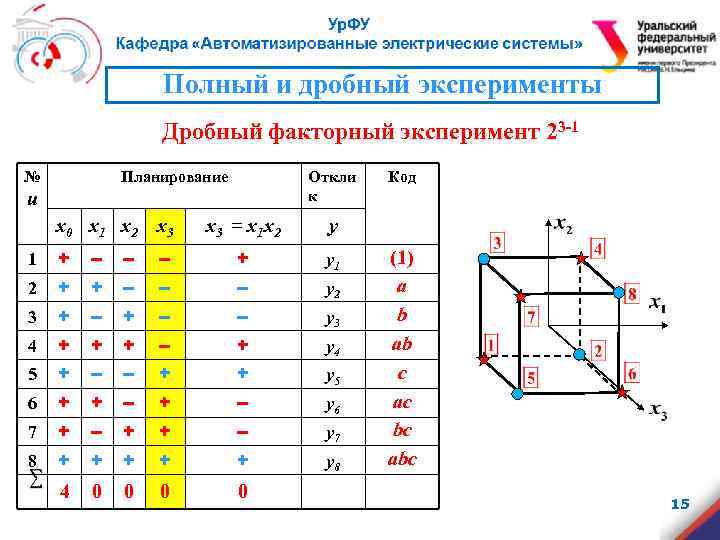Полный и дробный эксперименты Дробный факторный эксперимент 23 -1 № Планирование Откли к u x 0 x 1 x 2 x 3 = x 1 x 2 Код y 1 + – – – + y 1 2 + + – – – y 2 3 + – – y 3 4 + + + – + y 4 5 + – – + + y 5 6 + + – y 6 7 + – + + – y 7 8 + + + y 8 4 0 0 (1) a b ab с aс bс abс 15

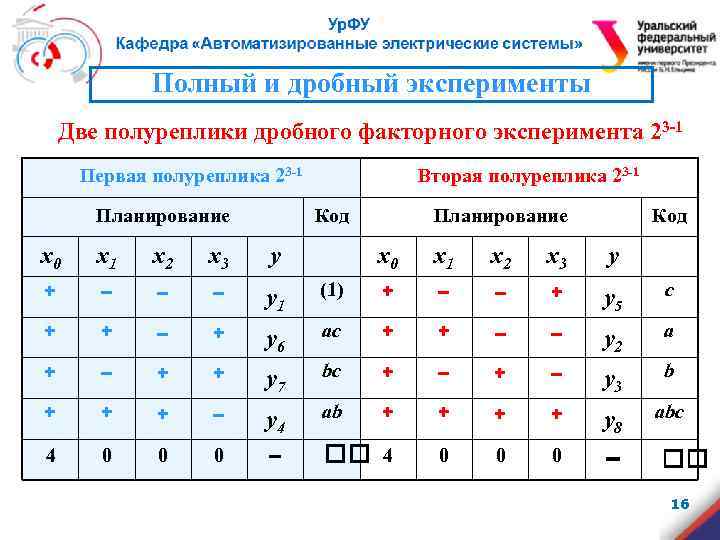Полный и дробный эксперименты Две полуреплики дробного факторного эксперимента 23 -1 Первая полуреплика 23 -1 Планирование Вторая полуреплика 23 -1 Код x 0 x 1 x 2 x 3 y + – – – y 1 + + – + + + 4 0 Планирование Код x 0 x 1 x 2 x 3 y (1) + – – + y 5 с y 6 aс + + – – y 2 a + y 7 bс + – y 3 b + – y 4 ab + + y 8 abс 0 0 – 4 0 0 0 – 16

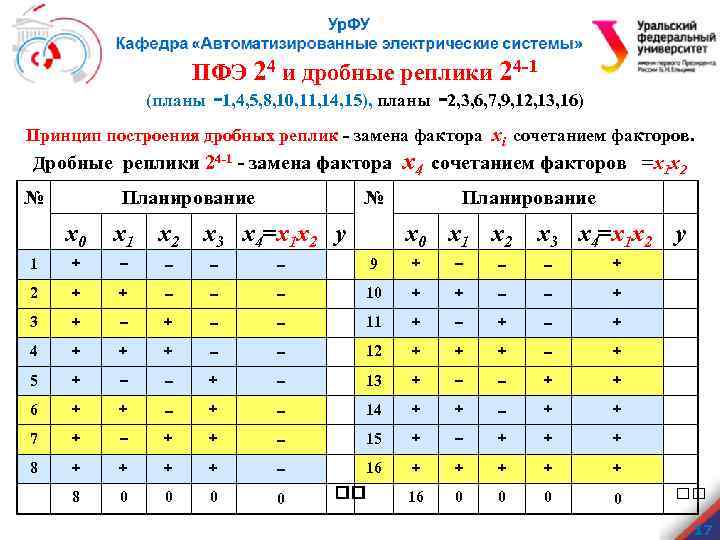ПФЭ 24 и дробные реплики 24 -1 (планы -1, 4, 5, 8, 10, 11, 14, 15), планы -2, 3, 6, 7, 9, 12, 13, 16) Принцип построения дробных реплик - замена фактора xi сочетанием факторов. Дробные реплики 24 -1 - замена фактора № Планирование x 4 сочетанием факторов =x 1 x 2 № x 3 x 4=x 1 x 2 y Планирование x 0 x 1 x 2 1 + – – 9 + – – – + 2 + + – – – 10 + + – – + 3 + – – 11 + – + 4 + + + – – 12 + + + – + 5 + – – + – 13 + – – + + 6 + + – 14 + + – + + 7 + – + + – 15 + – + + + 8 + + – 16 + + + 8 0 0 16 0 0 x 3 x 4=x 1 x 2 y 17

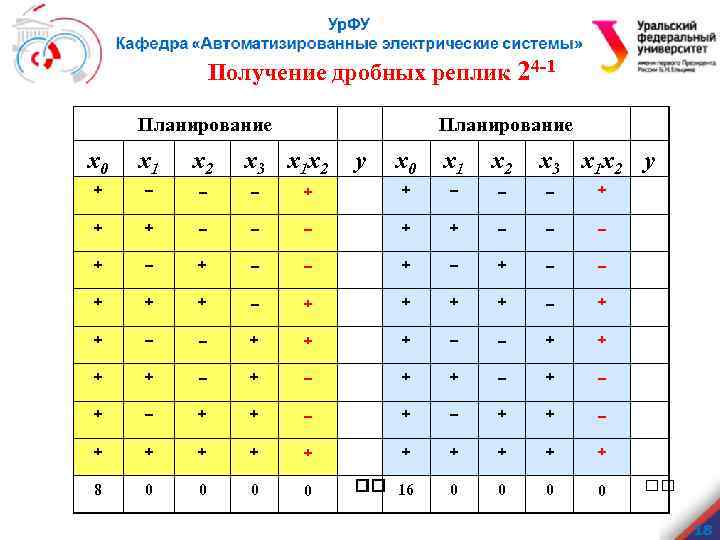Получение дробных реплик 24 -1 Планирование x 0 x 1 x 2 + – – – + + – + Планирование x 3 x 1 x 2 y x 0 x 1 x 2 x 3 x 1 x 2 y + + – – – + – – + + + + – – + + – + – + + + 8 0 0 16 0 0 18

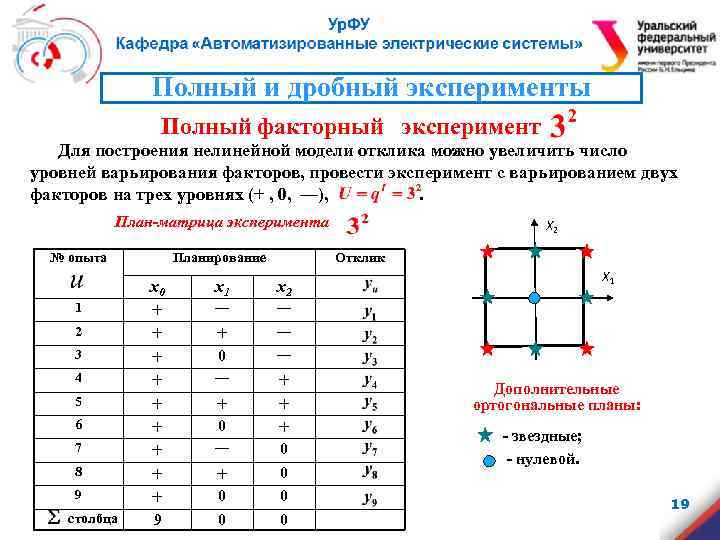Полный и дробный эксперименты Полный факторный эксперимент Для построения нелинейной модели отклика можно увеличить число уровней варьирования факторов, провести эксперимент с варьированием двух факторов на трех уровнях (+ , 0, —), . План-матрица эксперимента № опыта 1 2 3 4 5 6 7 8 9 столбца Планирование x 0 + + + + + 9 Х 2 Отклик x 1 — — + — 0 — — + + + Х 1 x 2 + 0 — + 0 0 0 Дополнительные ортогональные планы: - звездные; - нулевой. 19

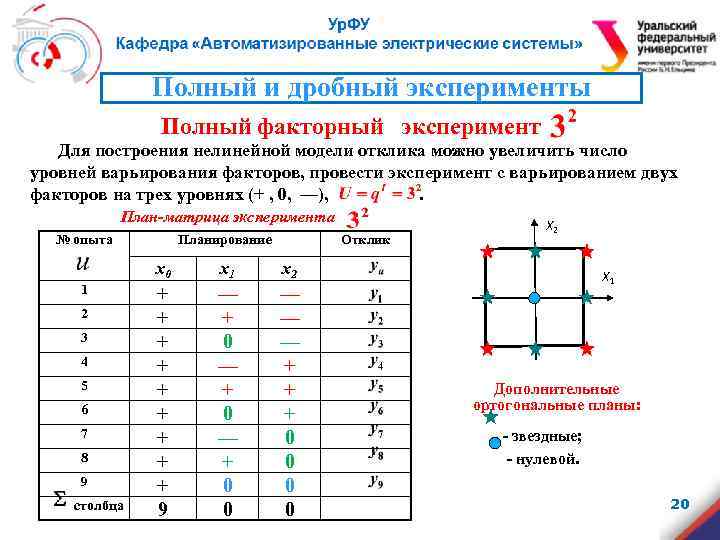Полный и дробный эксперименты Полный факторный эксперимент Для построения нелинейной модели отклика можно увеличить число уровней варьирования факторов, провести эксперимент с варьированием двух факторов на трех уровнях (+ , 0, —), . План-матрица эксперимента № опыта Планирование Отклик x 0 1 2 3 4 5 6 7 8 9 столбца x 1 x 2 + + + + + 9 — + 0 0 — — — + + + 0 0 Х 2 Х 1 Дополнительные ортогональные планы: - звездные; - нулевой. 20

Полный и дробный эксперименты Вывод При необходимости более точного учета нелинейности отклика можно увеличивать число уровней варьирования факторов и проводить активный эксперимент с варьированием факторов на трех, четырех и более ( ) уровнях. Для снижения трудоемкости эксперимента при увеличении числа уровней варьирования факторов обычно применяется дробный факторный эксперимент с использованием, при необходимости, звездных и нулевого планов.

Построение электросетевого блока оптимизационной модели

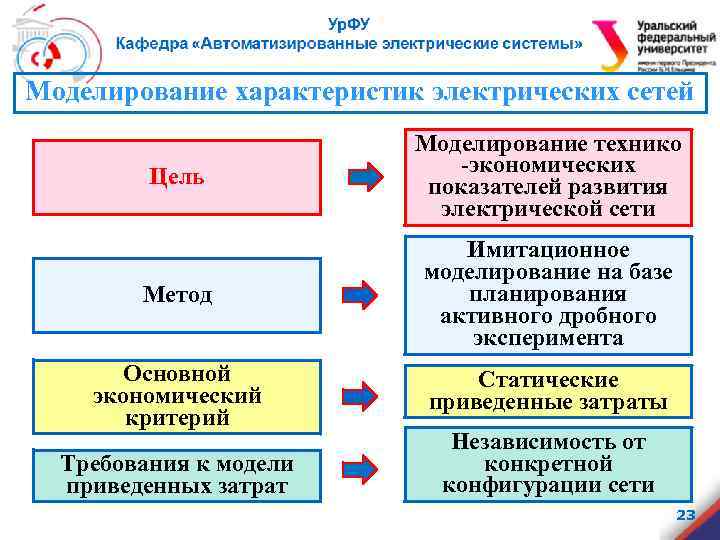Моделирование характеристик электрических сетей Цель Моделирование технико -экономических показателей развития электрической сети Метод Имитационное моделирование на базе планирования активного дробного эксперимента Основной экономический критерий Статические приведенные затраты Требования к модели приведенных затрат Независимость от конкретной конфигурации сети 23

Построение ЭСБ оптимизационной модели Обобщенные параметры, определяющие приведенные затраты в электрическую сеть Суммарная генерирующая мощность ОЭС Pг Средняя плотность нагрузок на территории ОЭС ρн Степень неравномерности распределения нагрузок по территории α Удельная протяженность существующих электрических сетей γ Момент электрических станций относительно центров нагрузок M Число сооружаемых электростанций n 24

Построение ЭСБ оптимизационной модели Вид модели приведенных затраты в электрическую сеть (3 блок оптимизационной модели развития генерирующих мощностей) Зсет = f(Pг, ρн, α, γ, M, n) Идея построения электросетевой модели Фиксированному сочетанию обобщенных параметров (строке план-матрицы активного эксперимента) соответствует определенное множество возможных реализаций конкретного расположения узлов генерации и нагрузок. 25

Определение диапазонов варьирования обобщенных параметров На основе анализа перспективных схем развития ОЭС на 15 -20 лет определены интервалы варьирования параметров: Pг = 6 – 18 ГВт; ρн = 24 – 48 к. Вт/км; α = 0 – 0, 25 отн. ед; γ = 4, 94 – 8 м/км 2; n = 1 – 4; M = (0 – 660) ∙ 106 МВт∙км Обобщенные параметры варьируются на двух уровнях. ПФЗ включает плана. Для снижения трудоемкости эксперимента используется ДФЭ. Учет нелинейности выполняется использованием нулевых и звездных точек. Общее число планов. 26

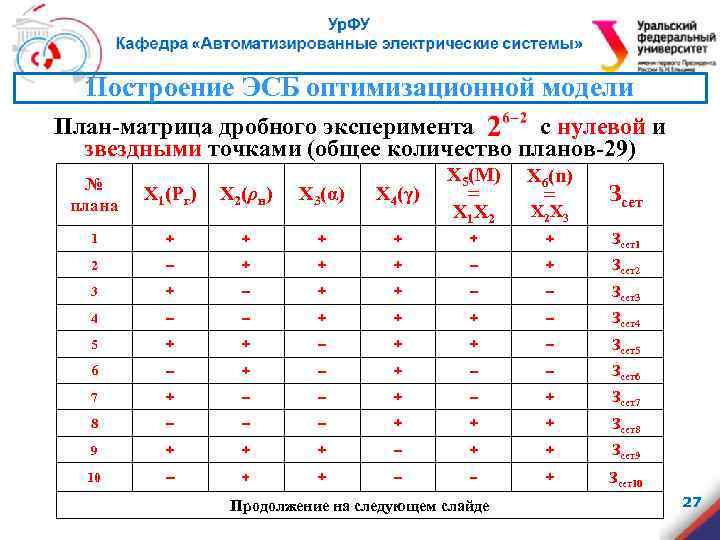Построение ЭСБ оптимизационной модели План-матрица дробного эксперимента с нулевой и звездными точками (общее количество планов-29) X 4(γ) X 5(M) = X 1 X 2 X 6(n) = Зсет + + Зсет1 + + + – + Зсет2 + – + + – – Зсет3 4 – – + + + – Зсет4 5 + + – Зсет5 6 – + – – Зсет6 7 + – – + Зсет7 8 – – – + + + Зсет8 9 + + + – + + Зсет9 10 – + + – – + Зсет10 № плана X 1(Pг) X 2(ρн) X 3(α) 1 + + 2 – 3 Продолжение на следующем слайде X 2 X 3 27

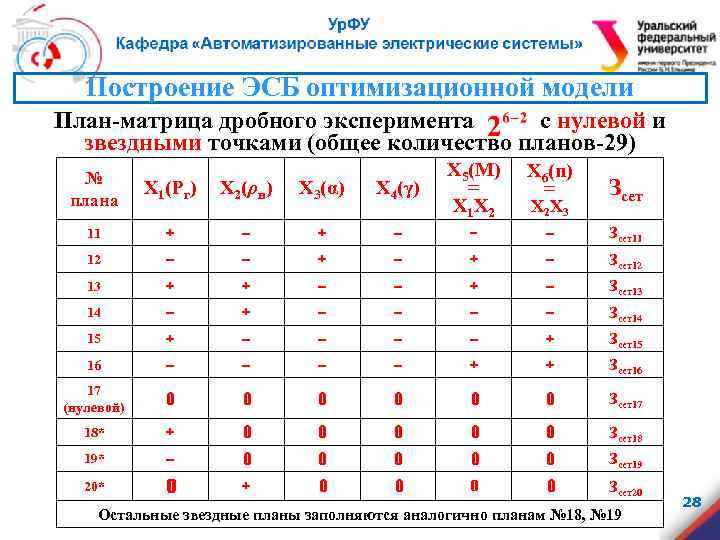Построение ЭСБ оптимизационной модели План-матрица дробного эксперимента с нулевой и звездными точками (общее количество планов-29) X 4(γ) X 5(M) = X 1 X 2 X 6(n) = Зсет + – – – Зсет11 – + – Зсет12 + + – – + – Зсет13 14 – + – – Зсет14 15 + – – + Зсет15 16 – – + + Зсет16 17 (нулевой) 0 0 0 Зсет17 18* + 0 0 0 Зсет18 19* – 0 0 0 Зсет19 20* 0 + 0 0 Зсет20 № плана X 1(Pг) X 2(ρн) X 3(α) 11 + – 12 – 13 X 2 X 3 Остальные звездные планы заполняются аналогично планам № 18, № 19 28

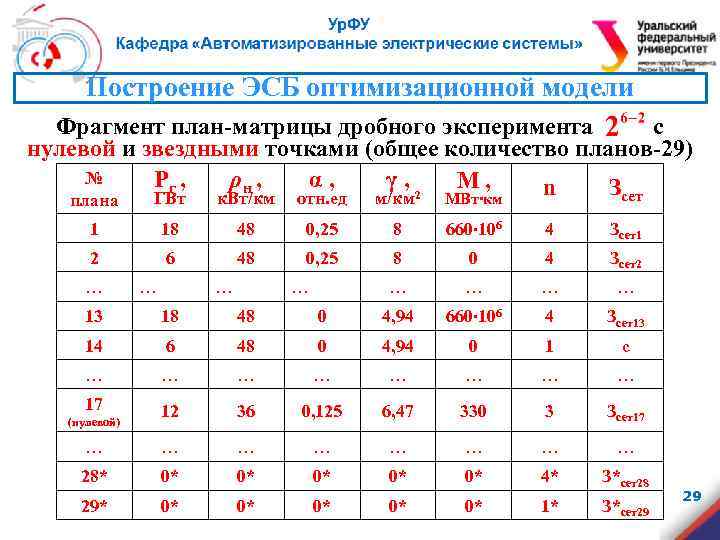Построение ЭСБ оптимизационной модели Фрагмент план-матрицы дробного эксперимента с нулевой и звездными точками (общее количество планов-29) № Pг , ρн , α, γ, M, n З 2 сет плана ГВт к. Вт/км отн. ед м/км МВт∙км 1 18 48 0, 25 8 660∙ 106 4 Зсет1 2 6 48 0, 25 8 0 4 Зсет2 … … … … 13 18 48 0 4, 94 660∙ 106 4 Зсет13 14 6 48 0 4, 94 0 1 с … … … … 17 12 36 0, 125 6, 47 330 3 Зсет17 … … … … 28* 0* 0* 0* 4* З*сет28 29* 0* 0* 0* 1* З*сет29 (нулевой) 29

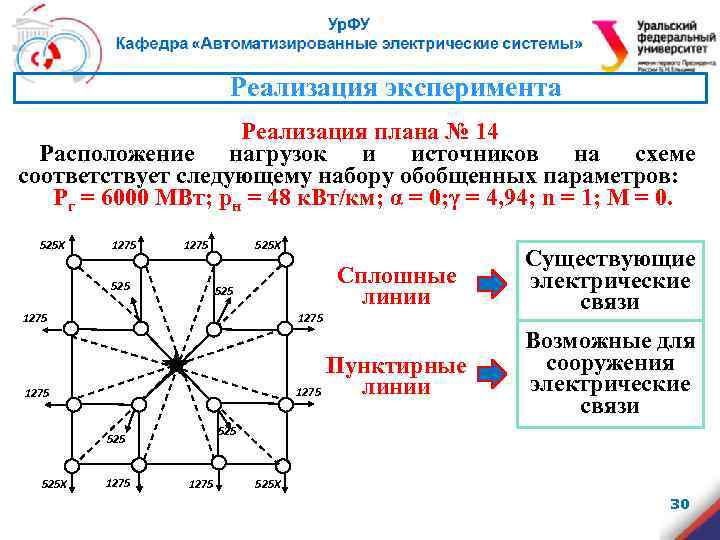Реализация эксперимента Реализация плана № 14 Расположение нагрузок и источников на схеме соответствует следующему набору обобщенных параметров: Pг = 6000 МВт; pн = 48 к. Вт/км; α = 0; γ = 4, 94; n = 1; M = 0. 525 Х 1275 525 Сплошные линии 525 1275 Пунктирные линии 1275 Возможные для сооружения электрические связи 525 525 Х Существующие электрические связи 1275 525 Х 30

Построение ЭСБ оптимизационной модели Формулы расчета обобщенных параметров J – номера генерирующих станций; е – номера нагрузок узлов; i – номера существующих электропередач; F – площадь территории ЭЭС; Li – длина i-й электропередачи; lj – расстояние от станции j до центра нагрузок; ki – коэффициент трансформации; 31

Построение ЭСБ оптимизационной модели Реализация каждого плана включает следующие этапы 1. Задание расположения узлов нагрузок по территории. 2. Определение мест сооружения электростанций. 3. Задание графа существующей электрической сети. 4. Задание избыточного графа проектируемой сети с учетом фактора надежности. 5. Выполнение оптимизации электрической сети. 6. Определение функции отклика - -приведенных затрат в системообразующую электрическую сеть. 32

Спасибо за внимание!