SUPPORT VECTOR MACHINES Jianping Fan Dept of Computer

SUPPORT VECTOR MACHINES Jianping Fan Dept of Computer Science UNC-Charlotte

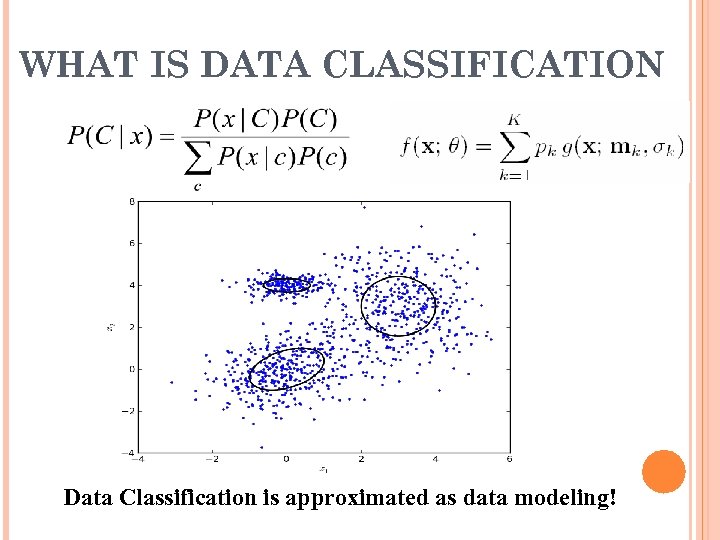WHAT IS DATA CLASSIFICATION Data Classification is approximated as data modeling!

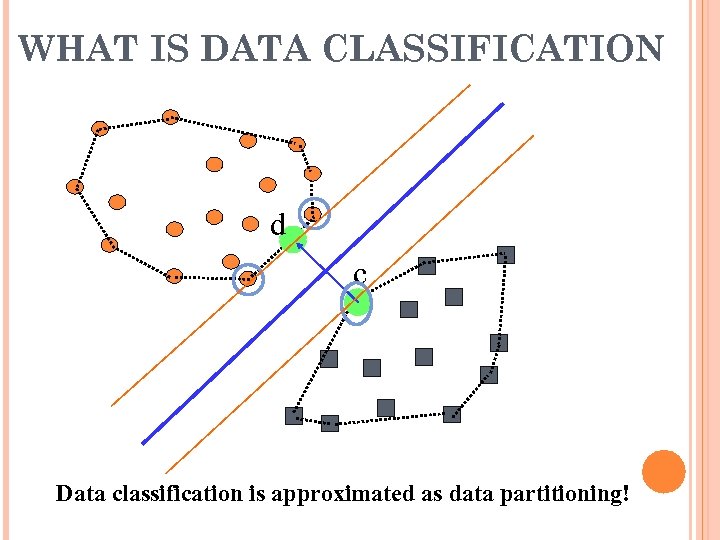WHAT IS DATA CLASSIFICATION d c Data classification is approximated as data partitioning!

WHAT IS DATA CLASSIFICATION What is the best modeling? What is the best partitioning? Discriminative vs. not-discriminative

WHICH OF THE LINEAR SEPARATORS IS OPTIMAL? Binary case

BEST LINEAR SEPARATOR?

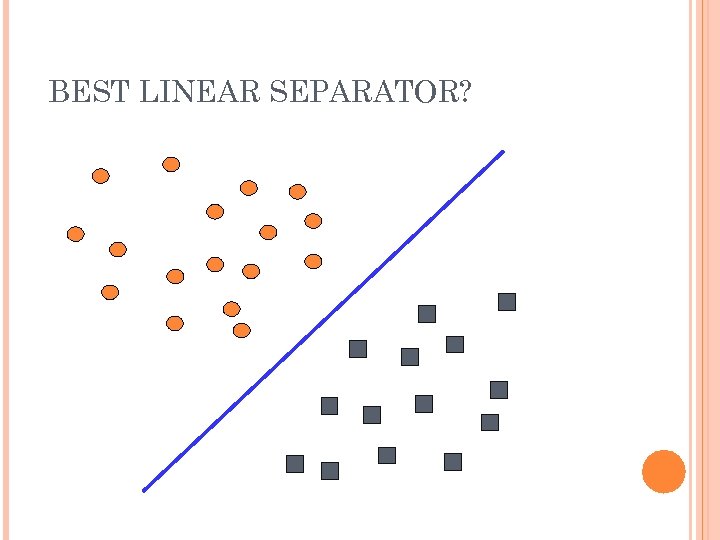BEST LINEAR SEPARATOR?

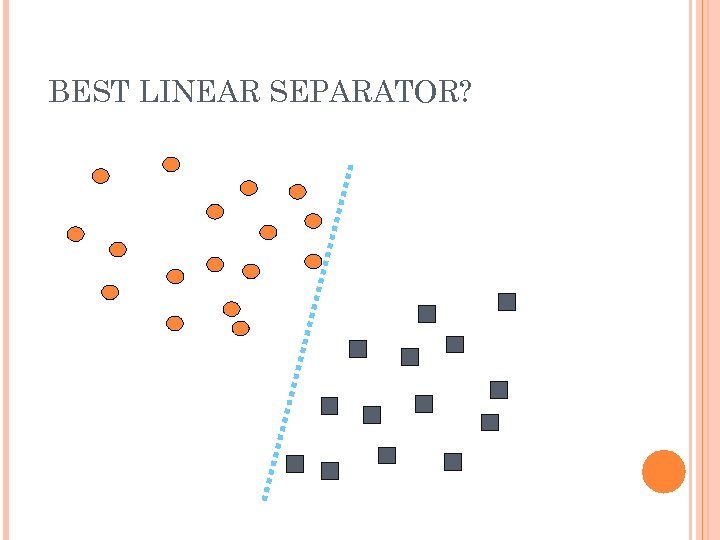BEST LINEAR SEPARATOR?

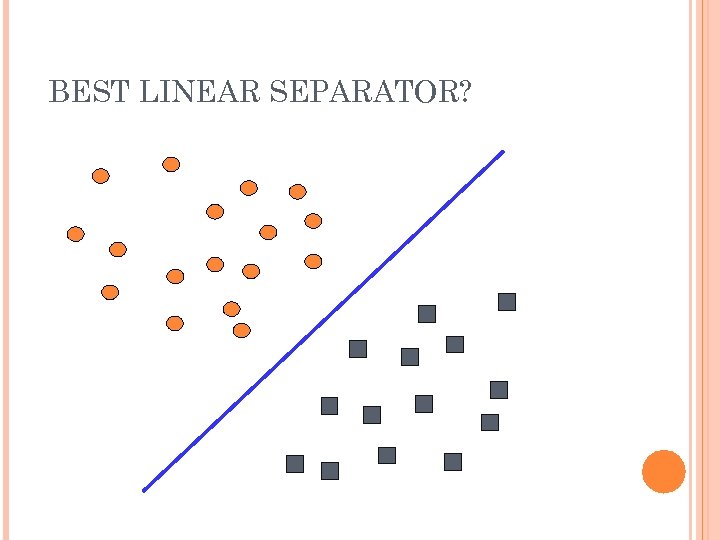BEST LINEAR SEPARATOR?

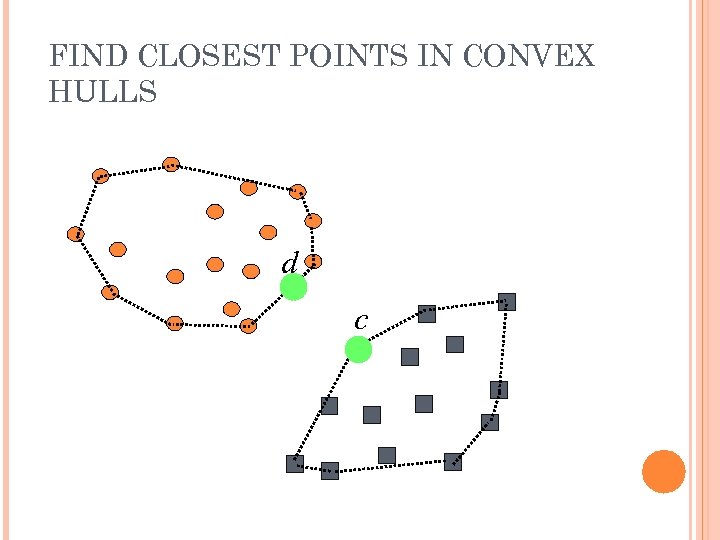FIND CLOSEST POINTS IN CONVEX HULLS d c

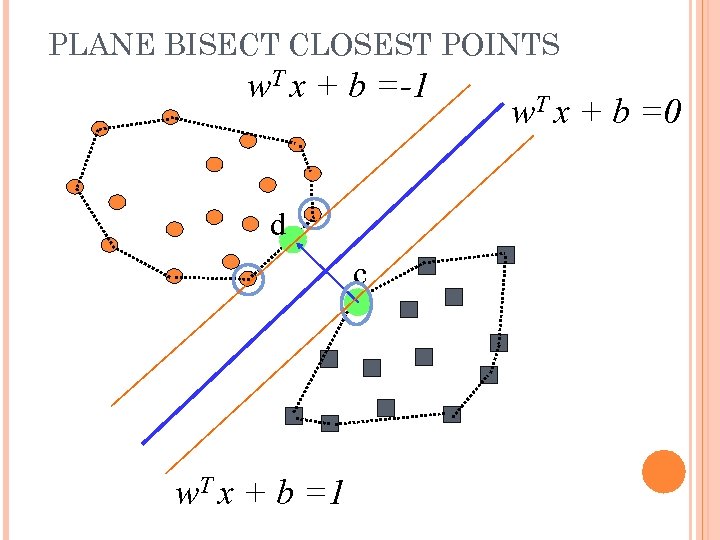PLANE BISECT CLOSEST POINTS w. T x + b =-1 d c w. T x + b =1 w. T x + b =0

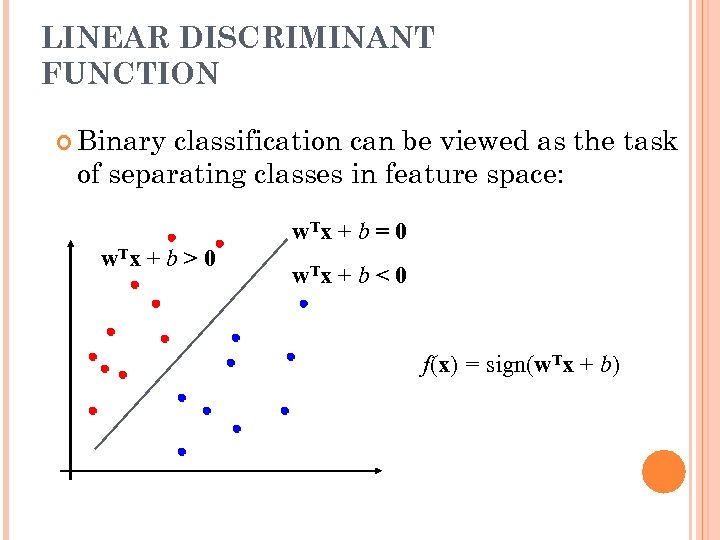LINEAR DISCRIMINANT FUNCTION Binary classification can be viewed as the task of separating classes in feature space: w. Tx + b = 0 w. Tx + b > 0 w. Tx + b < 0 f(x) = sign(w. Tx + b)

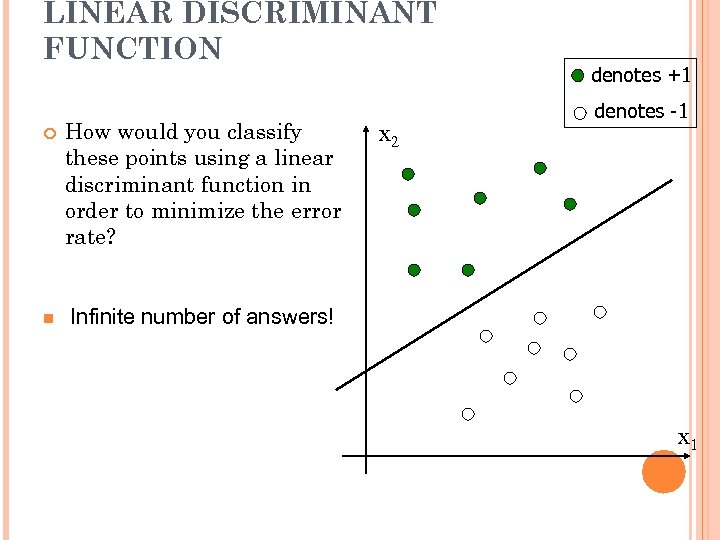LINEAR DISCRIMINANT FUNCTION How would you classify these points using a linear discriminant function in order to minimize the error rate? n denotes +1 denotes -1 Infinite number of answers! x 2 x 1

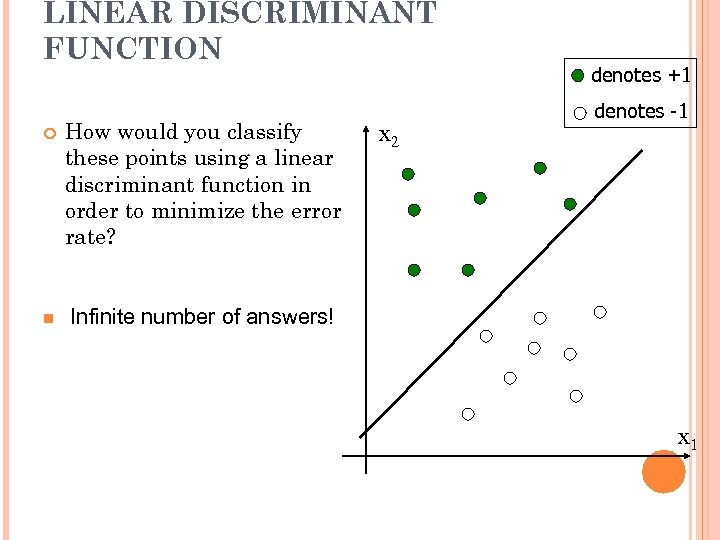LINEAR DISCRIMINANT FUNCTION How would you classify these points using a linear discriminant function in order to minimize the error rate? n denotes +1 denotes -1 Infinite number of answers! x 2 x 1

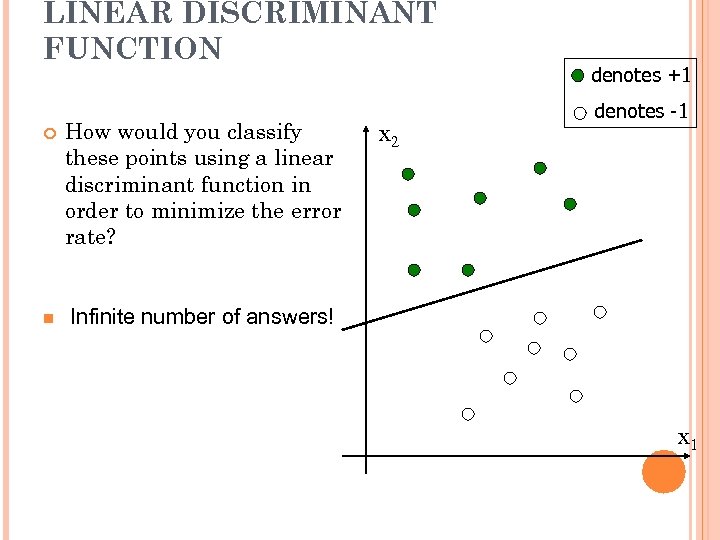LINEAR DISCRIMINANT FUNCTION How would you classify these points using a linear discriminant function in order to minimize the error rate? n denotes +1 denotes -1 Infinite number of answers! x 2 x 1

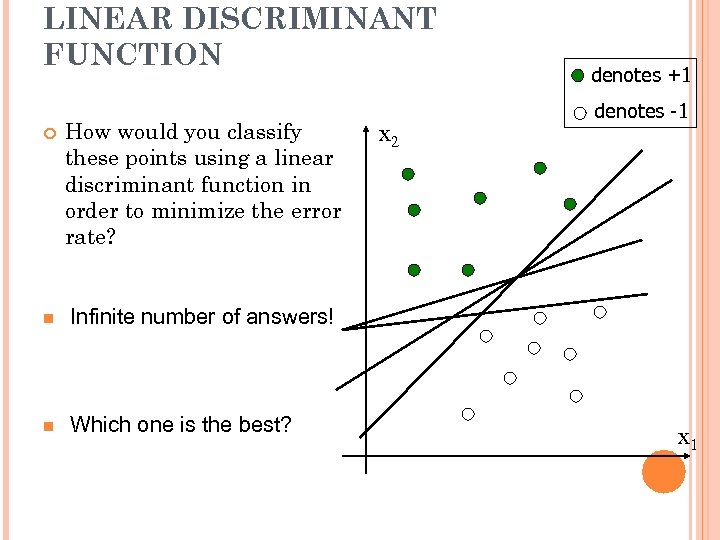LINEAR DISCRIMINANT FUNCTION How would you classify these points using a linear discriminant function in order to minimize the error rate? n Which one is the best? denotes -1 Infinite number of answers! n denotes +1 x 2 x 1

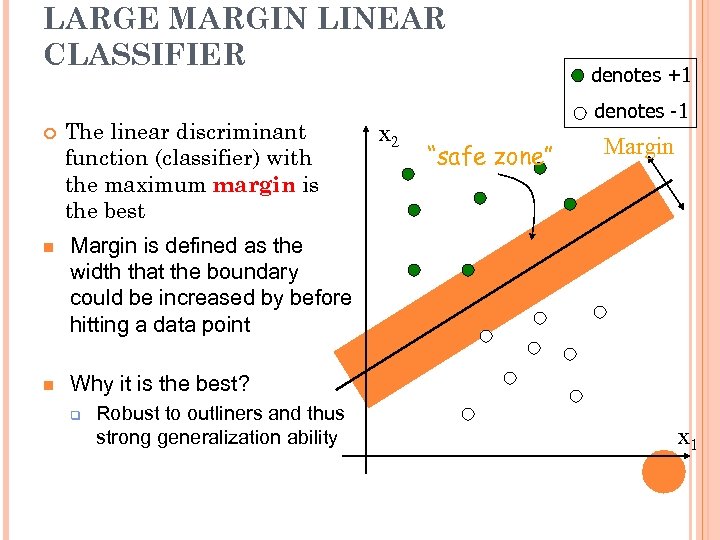LARGE MARGIN LINEAR CLASSIFIER The linear discriminant function (classifier) with the maximum margin is the best n denotes -1 “safe zone” Margin is defined as the width that the boundary could be increased by before hitting a data point n x 2 denotes +1 Why it is the best? q Robust to outliners and thus strong generalization ability x 1

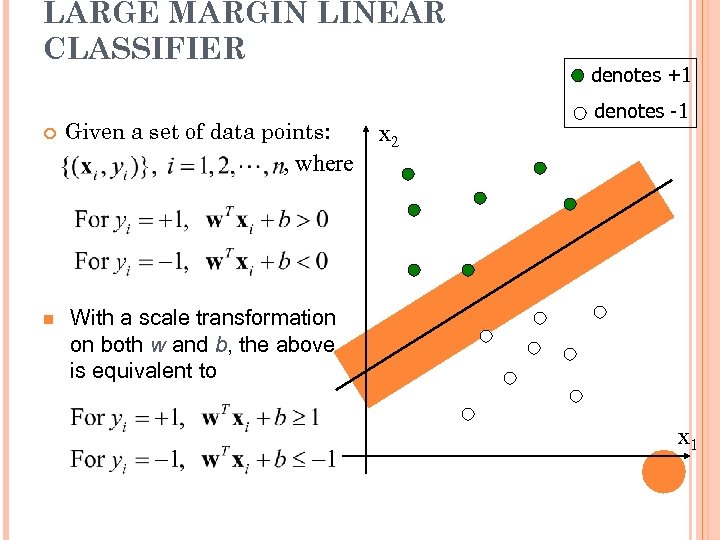LARGE MARGIN LINEAR CLASSIFIER Given a set of data points: , where n x 2 denotes +1 denotes -1 With a scale transformation on both w and b, the above is equivalent to x 1

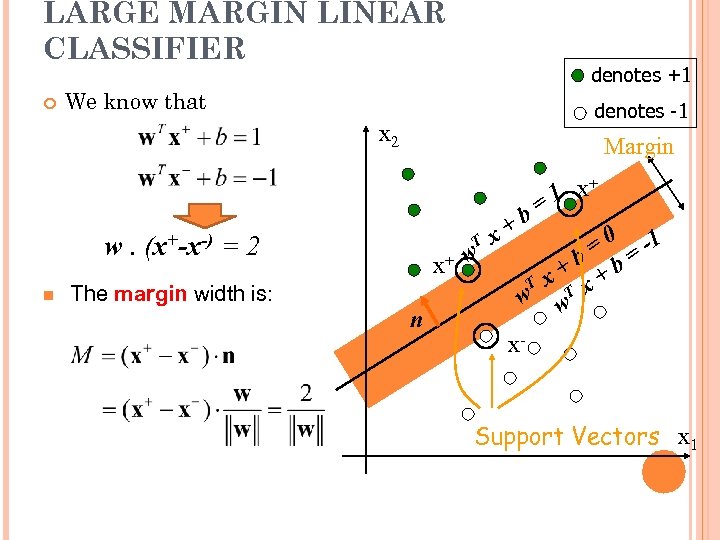LARGE MARGIN LINEAR CLASSIFIER denotes +1 We know that denotes -1 x 2 Margin w. (x+-x-) = 2 n The margin width is: T x+ w n +b x + 1 x = = 0 = -1 +b +b T x w w. T x x- Support Vectors x 1

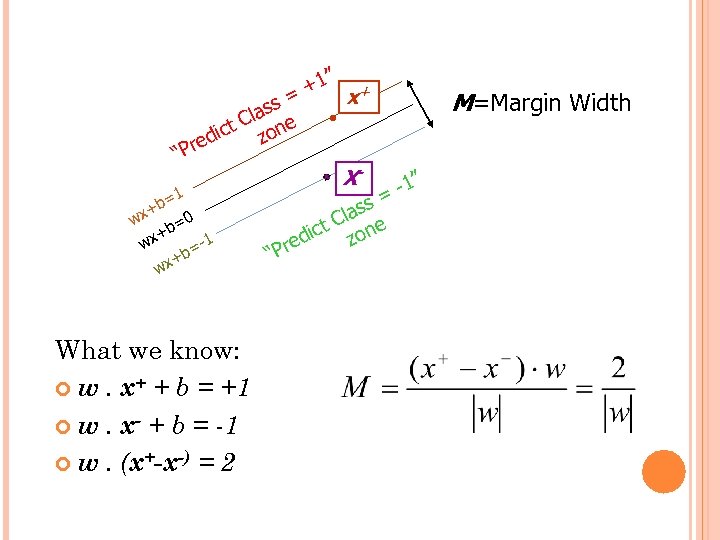” +1 x+ = ss Cla ne t dic zo e “Pr =1 b + wx X- =0 b + wx -1 = +b wx What we know: w. x+ + b = +1 w. x- + b = -1 w. (x+-x-) = 2 M=Margin Width -1” = “P s las C ict zone red

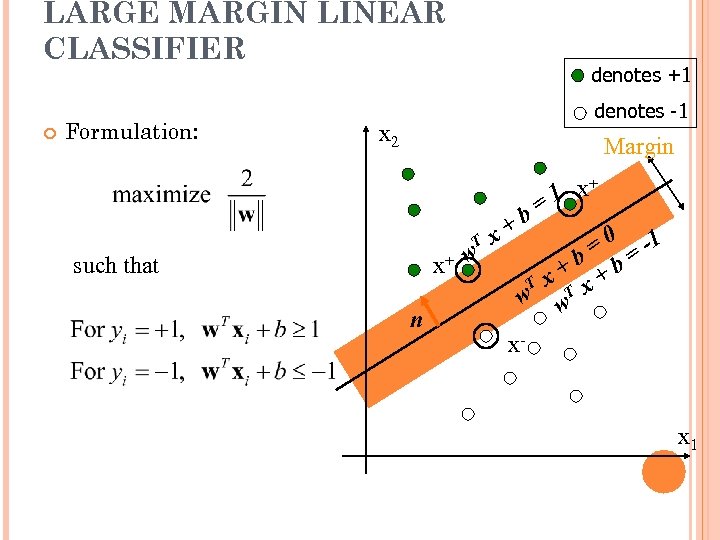LARGE MARGIN LINEAR CLASSIFIER Formulation: denotes +1 denotes -1 x 2 Margin T x+ w such that n +b x + 1 x = = 0 = -1 +b +b T x w w. T x x- x 1

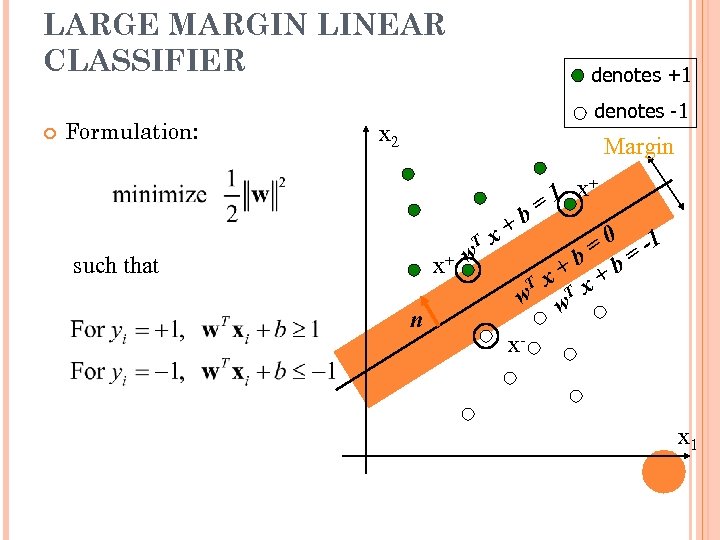LARGE MARGIN LINEAR CLASSIFIER Formulation: denotes +1 denotes -1 x 2 Margin T x+ w such that n +b x + 1 x = = 0 = -1 +b +b T x w w. T x x- x 1

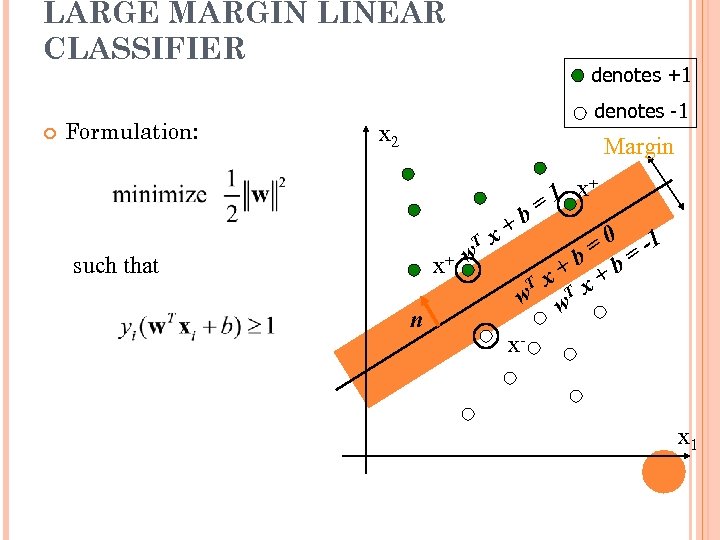LARGE MARGIN LINEAR CLASSIFIER Formulation: denotes +1 denotes -1 x 2 Margin T x+ w such that n +b x + 1 x = = 0 = -1 +b +b T x w w. T x x- x 1

SOLVING THE OPTIMIZATION PROBLEM Quadratic programming with linear constraints s. t. Lagrangian Function s. t.

SOLVING THE OPTIMIZATION PROBLEM s. t.

SOLVING THE OPTIMIZATION PROBLEM s. t. Lagrangian Dual Problem s. t. , and

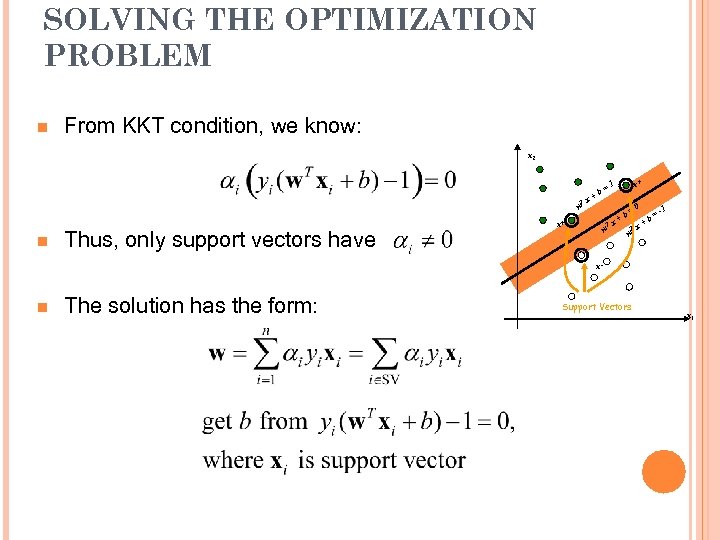SOLVING THE OPTIMIZATION PROBLEM n From KKT condition, we know: x 2 T w n Thus, only support vectors have x = +b x+ T w x+ 1 b x+ =0 T w x = +b -1 x- n The solution has the form: Support Vectors x 1

SOLVING THE OPTIMIZATION PROBLEM n The linear discriminant function is: n Notice it relies on a dot product between the test point x and the support vectors xi n Also keep in mind that solving the optimization problem involved computing the dot products xi. Txj between all pairs of training points

NON-IDEAL SITUATIONS n Data partitioning has mistakes, e. g. , positive samples locate in negative side or negative samples locate in positive side because decision boundaries are obtained by optimization n Data distributions have special or manifold structures, e. g. , data are not linearly separable

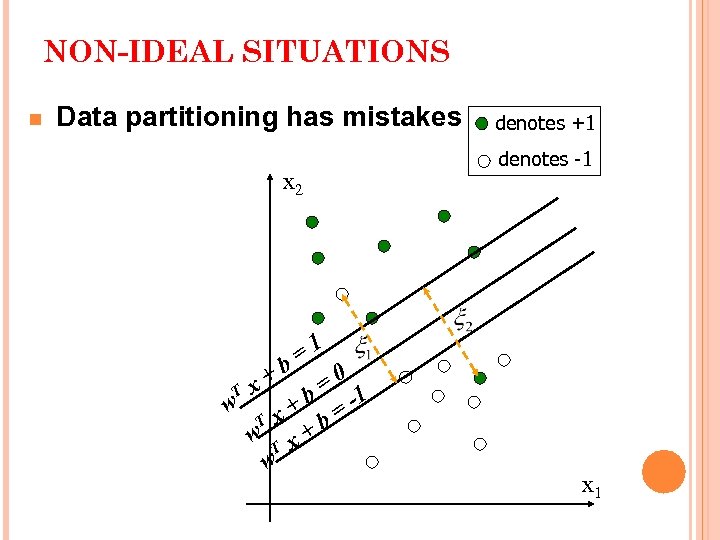NON-IDEAL SITUATIONS n Data partitioning has mistakes x 2 =1 +b =0 T x w + b = -1 T x b w T x+ w denotes +1 denotes -1 x 1

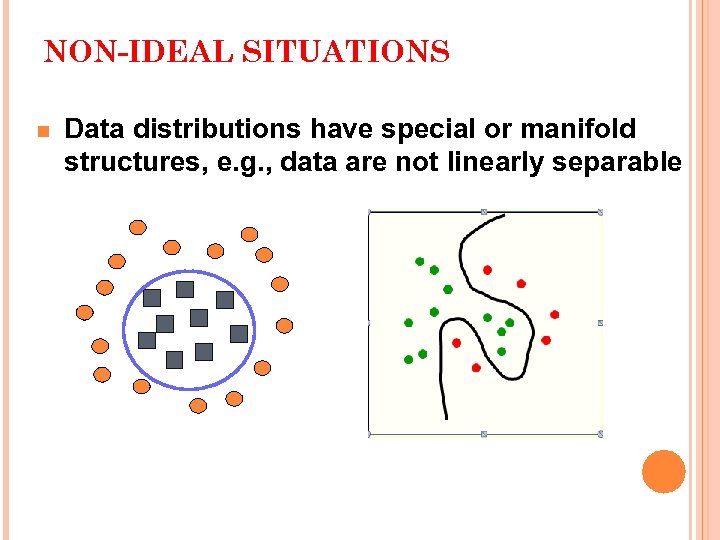NON-IDEAL SITUATIONS n Data distributions have special or manifold structures, e. g. , data are not linearly separable

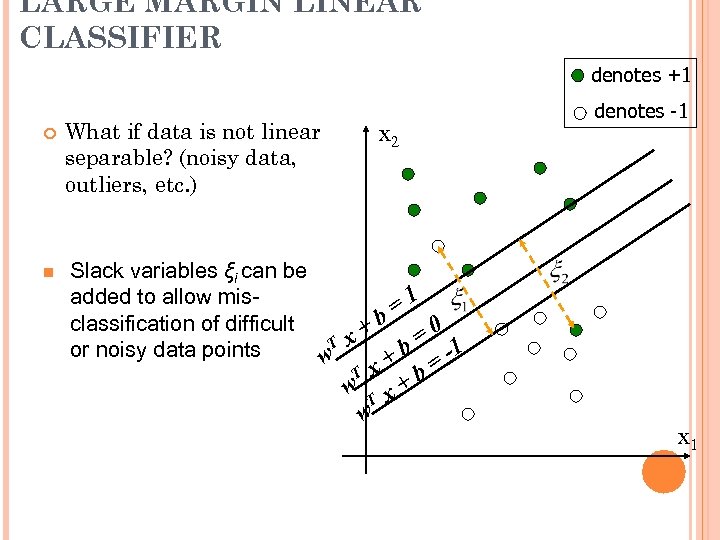LARGE MARGIN LINEAR CLASSIFIER denotes +1 n What if data is not linear separable? (noisy data, outliers, etc. ) x 2 denotes -1 Slack variables ξi can be added to allow mis=1 classification of difficult +b =0 T x or noisy data points w + b = -1 T w x T w +b x x 1

INTRODUCING SLACK VARIABLES Slack variables are constrained to be non-negative. When they are greater than zero they allow us to cheat by putting the plane closer to the datapoint than the margin. So we need to minimize the amount of cheating. This means we have to pick a value for lamba (this sounds familiar!)

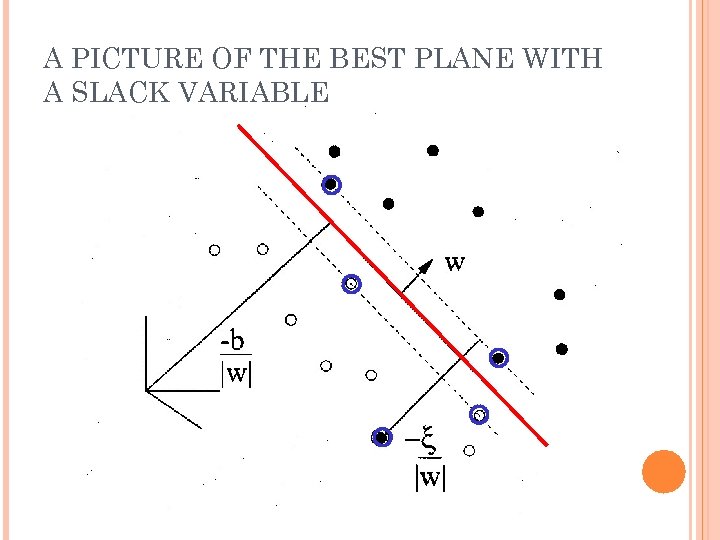A PICTURE OF THE BEST PLANE WITH A SLACK VARIABLE

LARGE MARGIN LINEAR CLASSIFIER n Formulation: such that n Parameter C can be viewed as a way to control over-fitting.

LARGE MARGIN LINEAR CLASSIFIER n Formulation: (Lagrangian Dual Problem) such that

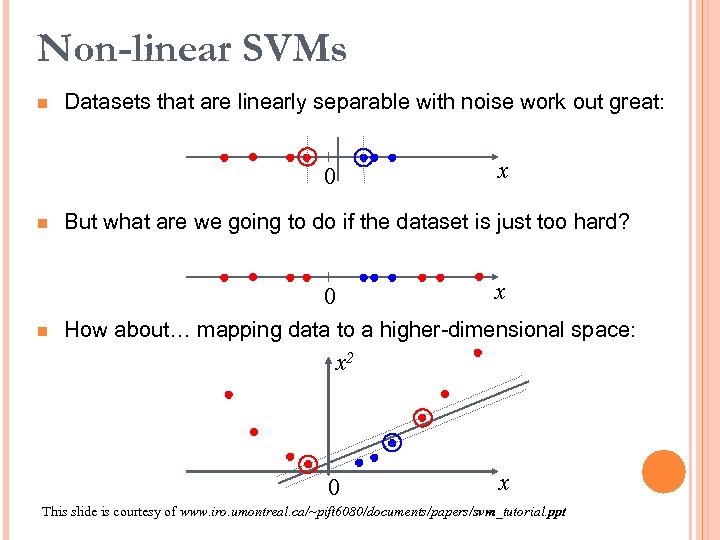Non-linear SVMs n Datasets that are linearly separable with noise work out great: 0 n But what are we going to do if the dataset is just too hard? 0 n x x How about… mapping data to a higher-dimensional space: x 2 0 x This slide is courtesy of www. iro. umontreal. ca/~pift 6080/documents/papers/svm_tutorial. ppt

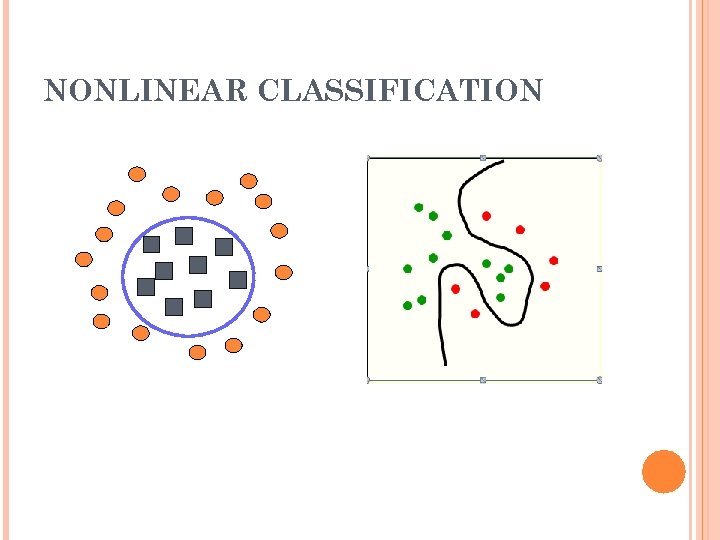NONLINEAR CLASSIFICATION

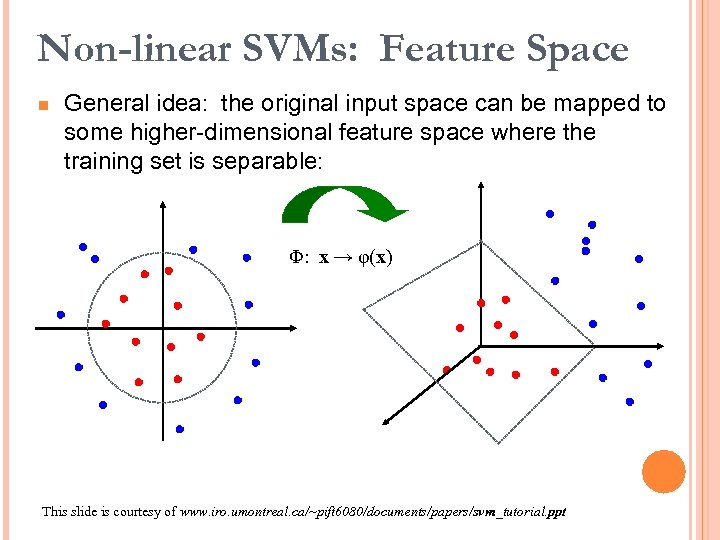Non-linear SVMs: Feature Space n General idea: the original input space can be mapped to some higher-dimensional feature space where the training set is separable: Φ: x → φ(x) This slide is courtesy of www. iro. umontreal. ca/~pift 6080/documents/papers/svm_tutorial. ppt

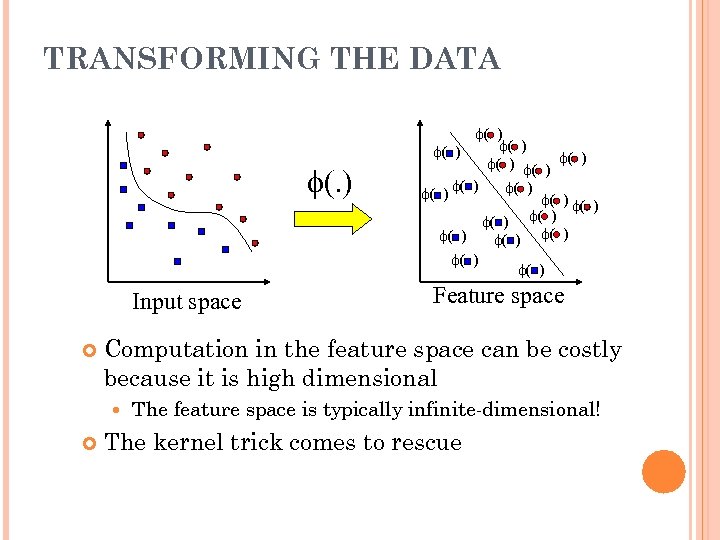TRANSFORMING THE DATA f(. ) Input space Feature space Computation in the feature space can be costly because it is high dimensional f( ) f( ) f( ) f( ) f( ) The feature space is typically infinite-dimensional! The kernel trick comes to rescue

Nonlinear SVMs: The Kernel Trick n With this mapping, our discriminant function is now: n No need to know this mapping explicitly, because we only use the dot product of feature vectors in both the training and test. n A kernel function is defined as a function that corresponds to a dot product of two feature vectors in some expanded feature space:

Nonlinear SVMs: The Kernel Trick n An example: 2 -dimensional vectors x=[x 1 x 2]; let K(xi, xj)=(1 + xi. Txj)2, Need to show that K(xi, xj) = φ(xi) Tφ(xj): K(xi, xj)=(1 + xi. Txj)2, = 1+ xi 12 xj 12 + 2 xi 1 xj 1 xi 2 xj 2+ xi 22 xj 22 + 2 xi 1 xj 1 + 2 xi 2 xj 2 = [1 xi 12 √ 2 xi 1 xi 22 √ 2 xi 1 √ 2 xi 2]T [1 xj 12 √ 2 xj 1 xj 22 √ 2 xj 1 √ 2 xj 2] = φ(xi) Tφ(xj), where φ(x) = [1 x 12 √ 2 x 1 x 2 x 22 √ 2 x 1 √ 2 x 2] This slide is courtesy of www. iro. umontreal. ca/~pift 6080/documents/papers/svm_tutorial. ppt

Nonlinear SVMs: The Kernel Trick n Examples of commonly-used kernel functions: q q Polynomial kernel: q Gaussian (Radial-Basis Function (RBF) ) kernel: q n Linear kernel: Sigmoid: In general, functions that satisfy Mercer’s condition can be kernel functions.

NONLINEAR SVM: OPTIMIZATION n Formulation: (Lagrangian Dual Problem) such that n The solution of the discriminant function is n The optimization technique is the same.

SUPPORT VECTOR MACHINE: ALGORITHM 1. Choose a kernel function 2. Choose a value for C 3. Solve the quadratic programming problem (many software packages available) 4. Construct the discriminant function from the support vectors

SOME ISSUES Choice of kernel - Gaussian or polynomial kernel is default - if ineffective, more elaborate kernels are needed - domain experts can give assistance in formulating appropriate similarity measures Choice of kernel parameters - e. g. σ in Gaussian kernel - σ is the distance between closest points with different classifications - In the absence of reliable criteria, applications rely on the use of a validation set or cross-validation to set such parameters. Optimization criterion – Hard margin v. s. Soft margin - a lengthy series of experiments in which various parameters are tested

STRENGTHS AND WEAKNESSES OF SVM Strengths Training is relatively easy No local optimal, unlike in neural networks It scales relatively well to high dimensional data Tradeoff between classifier complexity and error can be controlled explicitly Non-traditional data like strings and trees can be used as input to SVM, instead of feature vectors By performing logistic regression (Sigmoid) on the SVM output of a set of data can map SVM output to probabilities. Weaknesses Need to choose a “good” kernel function.

SUMMARY: SUPPORT VECTOR MACHINE 1. Large Margin Classifier Better generalization ability & less over-fitting 2. The Kernel Trick Map data points to higher dimensional space in order to make them linearly separable. Since only dot product is used, we do not need to represent the mapping explicitly.

ADDITIONAL RESOURCE http: //www. kernel-machines. org/

SOURCE CODE FOR SVM 1. SVM Light from Cornell University: Prof. Thorsten Joachims http: //svmlight. joachims. org/ 2. Multi-Class SVM from Cornell: Prof. Thorsten Joachims http: //svmlight. joachims. org/svm_multiclass. html 3. LIBSVM from Taiwan University: Prof. Chih-Jen Lin http: //www. csie. ntu. edu. tw/~cjlin/libsvm/

REFERENCES Duda R. O. and Hart P. E. ; Patter Classification and Scene Analysis. Wiley, 1973. T. M. Cover. Geometrical and statistical properties of systems of linear inequalities with applications in pattern recognition. IEEE Transactions on Electronic Computers}, 14: 326 -334, 1965. V. Vapnik and A. Lerner. Pattern recognition using generalized portrait method. Automation and Remote Control}, 24, 1963. V. Vapnik and A. Chervonenkis. A note on one class of perceptrons. Automation and Remote Control}, 25, 1964. J. K. Anlauf and M. Biehl. The adatron: an adaptive perceptron algorithm. Europhysics Letters, 10: 687 --692, 1989. N. Aronszajn. Theory of reproducing kernels. Transactions of the American Mathematical Society, 68: 337 --404, 1950. M. Aizerman, E. Braverman, and L. Rozonoer. Theoretical foundations of the potential function method in pattern recognition learning. Automation and Remote Control 25: 821 --837, 1964. O. L. Mangasarian. Linear and nonlinear separation of patterns by linear programming. Operations Research , 13: 444 --452, 1965. F. W. Smith. Pattern classifier design by linear programming. IEEE Transactions on Computers , C-17: 367 --372, 1968. C. Cortes and V. Vapnik. Support vector networks. Machine Learning, 20: 273 --297, 1995. V. Vapnik. The Nature of Statistical Learning Theory}. Springer Verlag, 1995. V. Vapnik. Statistical Learning Theory}. Wiley, 1998. A. N. Tikhonov and V. Y. Arsenin. Solutions of Ill-posed Problems. W. H. Winston, 1977. B. Schoelkopf, C. J. C. Burges, and A. J. Smola, Advances in kernel methods - support vector learning, MIT Press, Cambridge, MA, 1999. A. J. Smola, P. Bartlett, B. Schoelkopf, and C. Schuurmans, Advances in large margin classifiers, MIT Press, Cambridge, MA, 1999.

EXAMPLES OF KERNEL FUNCTIONS Linear: K(xi, xj)= xi. Txj Mapping Φ: x → φ(x), where φ(x) has dimensions Gaussian (radial-basis function): K(xi, xj) = x → φ(x), where φ(x) is x itself Polynomial of power p: K(xi, xj)= (1+ xi. Txj)p Mapping Φ: x → φ(x), where φ(x) is infinite-dimensional: every point is mapped to a function (a Gaussian); combination of functions for support vectors is the separator. Higher-dimensional space still has intrinsic dimensionality d (the mapping is not onto), but linear separators in it correspond to non-linear separators in original space.

Positive samples Negative samples y = 1 y = -1 For all samples We can put all these together to get optimization Primal form

We can solve the conditional maximum issue by means of non-negative Lagrange multipliers αi This problem can be solved by quadratic programming techniques

Dual form

Soft margin SVM classifier: This constraint along with the objective of minimizing Lagrange multipliers as done above. can be solved using

Kernel functions

THREE APPROACHES TO K-CLASS SVM

THREE APPROACHES TO K-CLASS SVM K one-versus-residue (OVR) binary SVM Advantages Disadvantages

THREE APPROACHES TO K-CLASS SVM Advantages Disadvantages

THREE APPROACHES TO K-CLASS SVM One K-Class SVM

K-class SVM 1 2 3

MULTI-CLASS SVM Intuitive formulation: without regularization / for the separable case Primal problem: QP Solved in the dual formulation, also Quadratic Program Main advantage: Sparsity (but not systematic) Drawbacks: • Speed with SMO (heuristic use of sparsity) • Need to recalculate or store xi. Txj • Sparse solutions • Outputs not probabilities

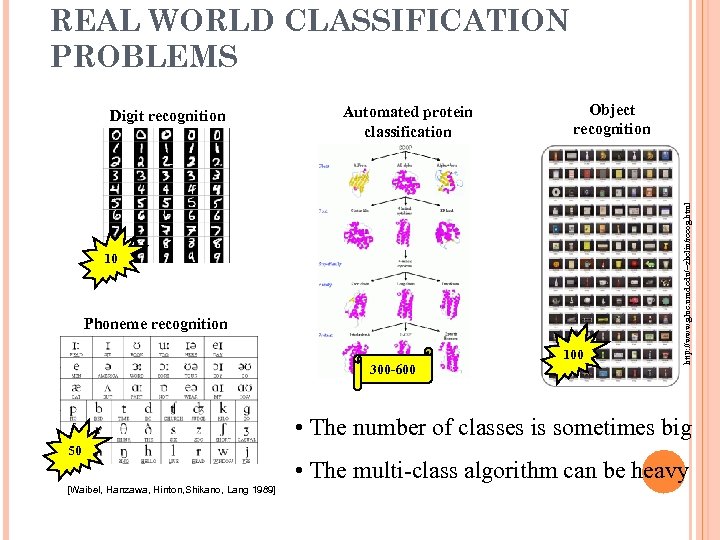REAL WORLD CLASSIFICATION PROBLEMS Automated protein classification Object recognition 10 Phoneme recognition 300 -600 100 http: //www. glue. umd. edu/~zhelin/recog. html Digit recognition • The number of classes is sometimes big 50 [Waibel, Hanzawa, Hinton, Shikano, Lang 1989] • The multi-class algorithm can be heavy

COMBINING BINARY CLASSIFIERS One-vs-all For each class build a classifier for that class vs the rest • Often very imbalanced classifiers (use asymmetric regularization) All-vs-all For each class build a classifier for that class vs the rest • A priori a large number of classifiers to build but… • The pairwise classification are way much faster • The classifications are balanced (easier to find the best regularization) … so that in many cases it is clearly faster than one-vs-all

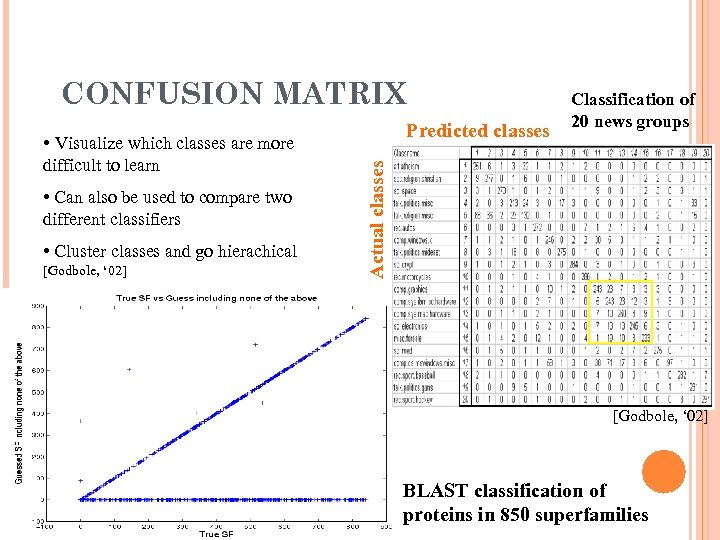CONFUSION MATRIX Predicted classes difficult to learn • Can also be used to compare two different classifiers • Cluster classes and go hierachical [Godbole, ‘ 02] Actual classes • Visualize which classes are more Classification of 20 news groups [Godbole, ‘ 02] BLAST classification of proteins in 850 superfamilies

CALIBRATION How to measure the confidence in a class prediction? Crucial for: 1. Comparison between different classifiers 2. Ranking the prediction for ROC/Precision-Recall curve 3. In several application domains having a measure of confidence for each individual answer is very important (e. g. tumor detection) Some methods have an implicit notion of confidence e. g. for SVM the distance to the class boundary relative to the size of the margin other like logistic regression have an explicit one.

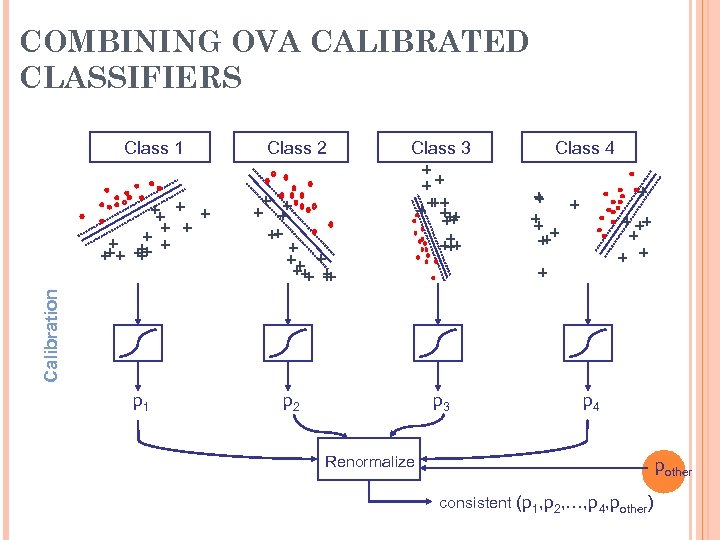COMBINING OVA CALIBRATED CLASSIFIERS + + + + ++ + ++ + Class 4 + + + ++ + Class 3 + ++ +++ + + + Class 2 Calibration Class 1 p 2 p 3 p 4 Renormalize pother consistent (p 1, p 2, …, p 4, pother)

EXPONENTIAL FORM Once the graph is defined the model can be written in exponential form parameter vector feature vector Comparing two labellings with the likelihood ratio

DISCRIMINATIVE ALGORITHMS

EXAMPLE: MULTICLASS SETTING Feature encoding: Predict: Update:

THREE APPROACHES TO K-CLASS SVM

GENERAL SVM Objective function = error function + regularization term

DEFINITION ‘Support Vector Machine is a system for efficiently training linear learning machines in kernel-induced feature spaces, while respecting the insights of generalisation theory and exploiting optimisation theory. ’ AN INTRODUCTION TO SUPPORT VECTOR MACHINES (and other kernelbased learning methods) N. Cristianini and J. Shawe-Taylor Cambridge University Press 2000 ISBN: 0 521 78019 5 Kernel Methods for Pattern Analysis John Shawe-Taylor & Nello Cristianini Cambridge University Press, 2004

PROBLEMS OF SVM Binary and hard to be extended for multi-class Cost-sensitive to number of training samples How to use GMM to improve SVM?

PROBLEMS OF GMM Not-discriminative How to use SVM to improve GMM?