Support Vector Machine Applications Electrical Load Forecasting ICONS

Support Vector Machine Applications Electrical Load Forecasting ICONS Presentation Spring 2007 N. Sapankevych 20 April N. Sapankevych - 20 April 2007

SVMs and Electrical Load Forecasting l l l 2 AGENDA Research Status SVMs, Time Series Prediction, and Electrical Load Forecasting Relevance Vector Machines Way forward Q&A N. Sapankevych - 20 April 2007

SVMs and Electrical Load Forecasting l SVM time series prediction survey complete – – l Major research focuses on financial market forecasting and electrical load prediction Paper to be submitted to IEEE Neural Network Journal Research focus on Support Vector Machines (SVMs) and their applications for time series prediction – l Expand to Relevance Vector Machines Thesis topic definition – Apply SVM time series prediction research l – Expand research to use relevance vector machines Potential collaboration w/ Prof. Domijan and Prof. Islam of USF EE Department l 3 RESEARCH OVERVIEW Electrical energy consumption prediction and resource management allocation wrt severe weather N. Sapankevych - 20 April 2007

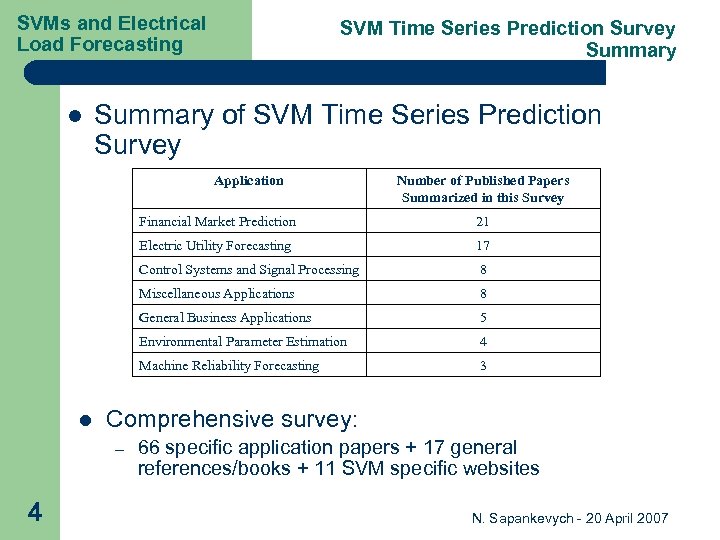SVMs and Electrical Load Forecasting l SVM Time Series Prediction Survey Summary of SVM Time Series Prediction Survey Application Number of Published Papers Summarized in this Survey Financial Market Prediction Electric Utility Forecasting 8 Miscellaneous Applications 8 General Business Applications 5 Environmental Parameter Estimation 4 Machine Reliability Forecasting 3 Comprehensive survey: – 4 17 Control Systems and Signal Processing l 21 66 specific application papers + 17 general references/books + 11 SVM specific websites N. Sapankevych - 20 April 2007

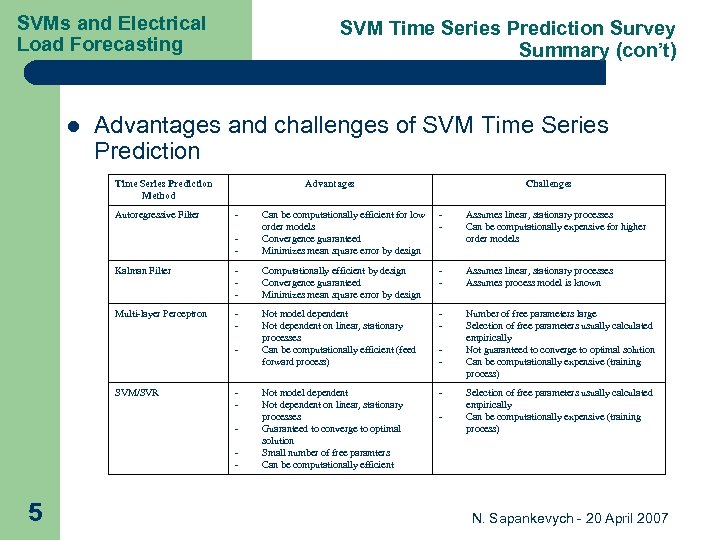SVMs and Electrical Load Forecasting l SVM Time Series Prediction Survey Summary (con’t) Advantages and challenges of SVM Time Series Prediction Method Advantages - - Can be computationally efficient for low order models Convergence guaranteed Minimizes mean square error by design Assumes linear, stationary processes Can be computationally expensive for higher order models Kalman Filter - Computationally efficient by design Convergence guaranteed Minimizes mean square error by design - Assumes linear, stationary processes Assumes process model is known Multi-layer Perceptron - Not model dependent Not dependent on linear, stationary processes Can be computationally efficient (feed forward process) - Number of free parameters large Selection of free parameters usually calculated empirically Not guaranteed to converge to optimal solution Can be computationally expensive (training process) Not model dependent Not dependent on linear, stationary processes Guaranteed to converge to optimal solution Small number of free paramters Can be computationally efficient - Autoregressive Filter - Challenges - SVM/SVR - 5 - - Selection of free parameters usually calculated empirically Can be computationally expensive (training process) N. Sapankevych - 20 April 2007

SVMs and Electrical Load Forecasting l Seventeen papers reviewed and documented for electrical load prediction using SVMs – l Should note more than half of them use same general approach but different data set Majority of papers use same basic approach to predict (short term) electrical load demand – – Some models use weather trends as inputs Free parameters determined empirically l – 6 RMSE, MAPE Prediction horizons short – l Note for the same kernel functions selected, different numerical values found empirically for different applications No set metrics for measures of effectiveness – l A few papers propose use of other algorithms, such as genetic algorithms and simulated annealing, to assist in parameter selection The accurate and optimal selection of the free parameters remains the challenge for SVM Time Series Prediction l l SVM Time Series Prediction Electrical Load Forecasting Summary Typically less than seven samples No error estimate in prediction (for all applications) N. Sapankevych - 20 April 2007

SVMs and Electrical Load Forecasting l Developed by Tipping in 1999 – l Michael E. Tipping, The Relevance Vector Machine, patent number 6633857 (Microsoft Research) Work focused on addressing SVM disadvantages – No probabilistic output l Uncertainty of prediction (regression) or classification (binary selection) not given – – – 7 Relevance Vector Machines Although, distance from maximum hyperplane (as example) could infer accuracy? In general, need to empirically determine errors relative to free parameters Specific rules related to generating kernel functions (Mercer’s conditions) N. Sapankevych - 20 April 2007

SVMs and Electrical Load Forecasting l l l Formulation uses same form as SVM, but a Bayesian framework is adopted Goal, from a regression (and ultimately a time series prediction application) point of view, is to provide the predicted “state” as well as an estimate of the uncertainty There is an underlying assumption in this formulation is that Gaussian statistics are assumed for prediction – 8 Relevance Vector Machines (con’t) SVM Architecture Can this assumption hold for highly non-linear, non-stationary systems? N. Sapankevych - 20 April 2007

SVMs and Electrical Load Forecasting l Relevance Vector Machines (con’t) The formulation outline below is summarized from: M. E. Tipping, “The Relevance Vector Machine”, Advances in Neural Information Processing Systems 12, pages 652 -658. MIT Press, 2000. l Recall formulation of regression function using SVM l Goal of SVM to determine optimal weights w – – l Now assume Gaussian distribution for targets – 9 Define input vectors xn and “targets” tn The targets t are the training data (output) based on the input vector x P(t|x) is Gaussian: N(t|y(x), s 2) N. Sapankevych - 20 April 2007

SVMs and Electrical Load Forecasting l The likelihood of the data set can be expressed as: – l – 10 p(w|t, a, s 2) The integration of this equation (over the weights) produces the marginal likelihood (evidence) – l p(t|w, s 2) maximize this likelihood By introducing hyperparameters an (necessary to avoid over-fitting) and applying Bayes rule, the posterior probability is generated – l Relevance Vector Machines (con’t) p(t|a, s 2) Note that Tipping states that integrating out the remaining two priors can not be done in closed form, and proposes another procedure (see ref) Goal now is to optimize the hyperparameters and estimate the noise variance N. Sapankevych - 20 April 2007

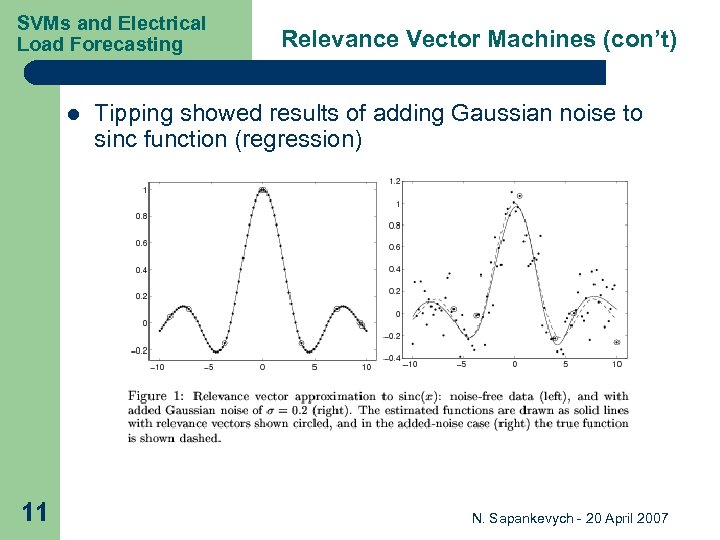SVMs and Electrical Load Forecasting l 11 Relevance Vector Machines (con’t) Tipping showed results of adding Gaussian noise to sinc function (regression) N. Sapankevych - 20 April 2007

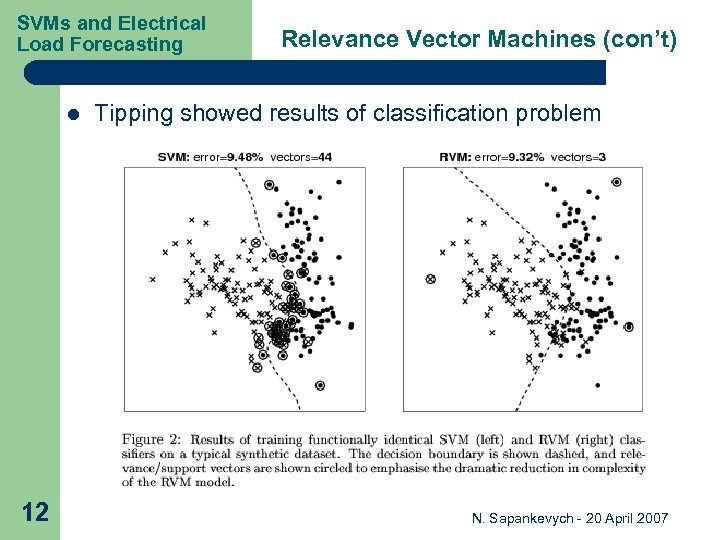SVMs and Electrical Load Forecasting l 12 Relevance Vector Machines (con’t) Tipping showed results of classification problem N. Sapankevych - 20 April 2007

SVMs and Electrical Load Forecasting l Why use RVMs? – – l Training more complex with Bayesian framework Questions – 13 More sparse representation of the data Can be more accurate Kernel function selection not as stringent (Mercer’s Theorem – Kernel matrix positive semidefinite, etc. ) Uncertainty of estimate now provided Drawbacks – l Relevance Vector Machines (con’t) Is Gaussian assumption on training data representative of applications where SVM is used? N. Sapankevych - 20 April 2007

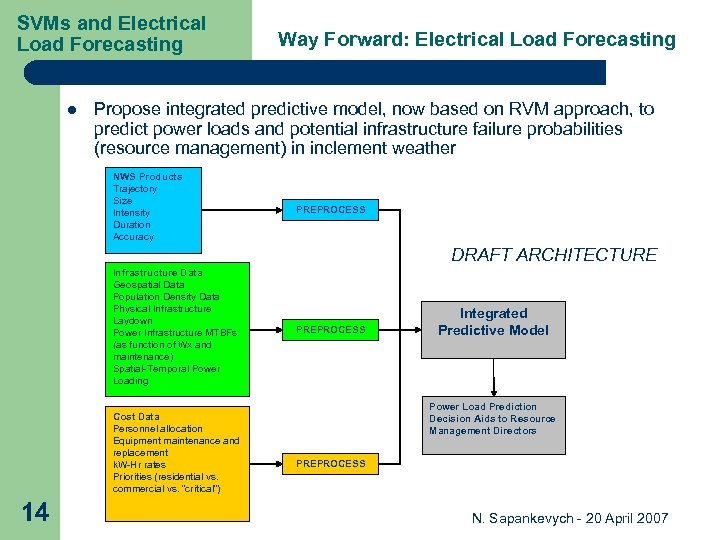SVMs and Electrical Load Forecasting l Way Forward: Electrical Load Forecasting Propose integrated predictive model, now based on RVM approach, to predict power loads and potential infrastructure failure probabilities (resource management) in inclement weather NWS Products Trajectory Size Intensity Duration Accuracy PREPROCESS DRAFT ARCHITECTURE Infrastructure Data Geospatial Data Population Density Data Physical Infrastructure Laydown Power Infrastructure MTBFs (as function of Wx and maintenance) Spatial-Temporal Power Loading Cost Data Personnel allocation Equipment maintenance and replacement k. W-Hr rates Priorities (residential vs. commercial vs. “critical”) 14 PREPROCESS Integrated Predictive Model Power Load Prediction Decision Aids to Resource Management Directors PREPROCESS N. Sapankevych - 20 April 2007

SVMs and Electrical Load Forecasting l What needs to be done – – Publish survey paper (final review w/ Prof. Sankar today – per request) Work w/ Prof. Sankar, Prof. Domijan and Prof. Islam to: l l – Clearly define thesis topic Define and obtain necessary data (at least on electrical load side of problem) Develop RVM approach to problem l Compare to SVM? Compare to other models (MLP, ARMA, other? ) Implement simulation Review thesis topic w/ committee members l 15 Way Forward: Electrical Load Forecasting Get buy-in N. Sapankevych - 20 April 2007

SVMs and Electrical Load Forecasting l Alexander – 16 Q&A 19 months and getting bigger! N. Sapankevych - 20 April 2007