Summary of one-locus fitness models Fitnesses Outcome WAa

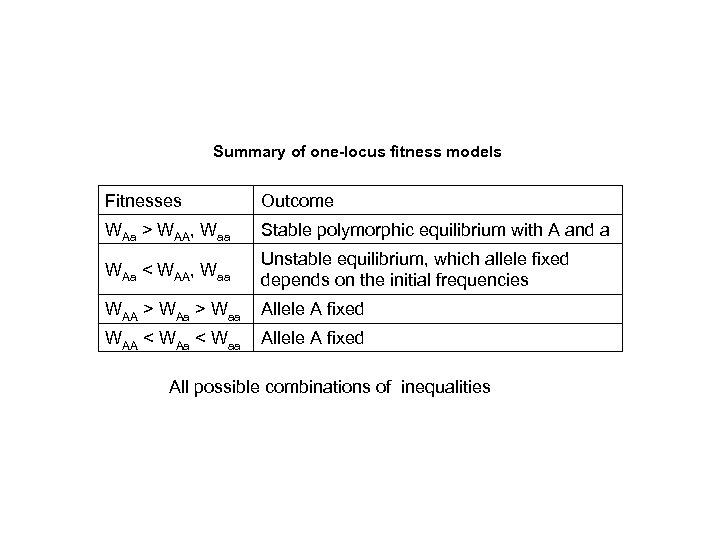Summary of one-locus fitness models Fitnesses Outcome WAa > WAA, Waa Stable polymorphic equilibrium with A and a WAa < WAA, Waa Unstable equilibrium, which allele fixed depends on the initial frequencies WAA > WAa > Waa Allele A fixed WAA < WAa < Waa Allele A fixed All possible combinations of inequalities

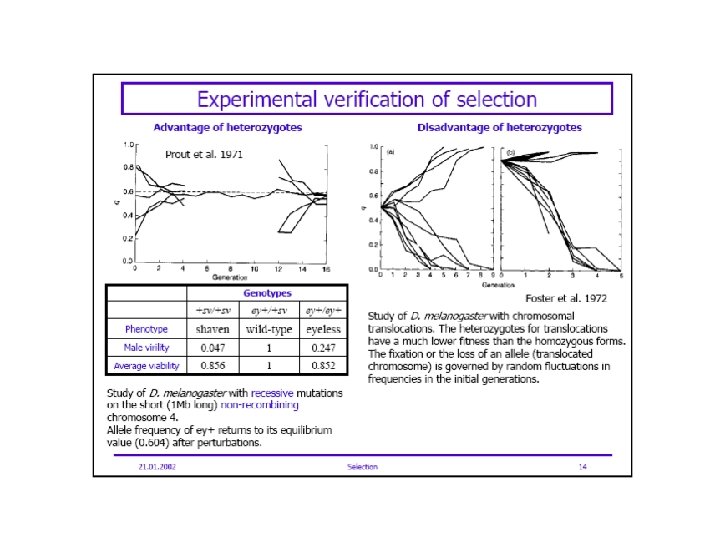
FITNESS How do we measure fitness? Survival # offspring per year Ability to acquire resources # mates Lifetime reproductive success: # mature offspring produced LRS = Lifespan of organism X Reproduction rate X Survival of young to adulthood

Possible genotypes AA, Aa, aa Possible phenotypes (1) The neutral one, where the only class is {AA, aa, Aa}; (2) The separative one: {AA} {aa} {Aa}; (3) The Mendel dominant one: {AA, Aa} and {aa}; (4) {AA aa} and {Aa}. In case (4) the phenotypes can be identified with the numbers of different genes and then ϕAA = ϕaa = 1, ϕAa = 2. For this reason we call this phenotypical structure quantitative.

Fitnesses Outcome WAa > WAA, Waa Stable polymorphic equilibrium with A and a WAa < WAA, Waa Unstable equilibrium, which allele fixed depends on the initial frequencies WAA > WAa > Waa Allele A fixed WAA < WAa < Waa Allele A fixed (1) The neutral one, where the only class is {AA, aa, Aa}; Formal fitness coefficient W 11(AA)= W 12(Aa)= W 22(aa) (=1)

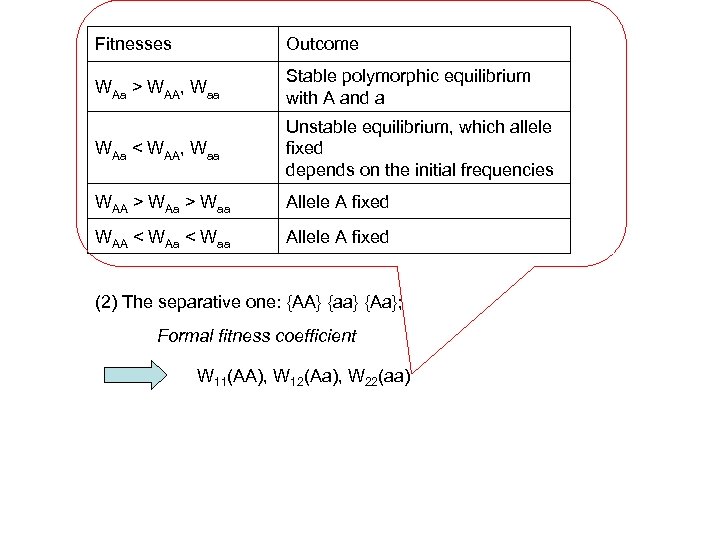Fitnesses Outcome WAa > WAA, Waa Stable polymorphic equilibrium with A and a WAa < WAA, Waa Unstable equilibrium, which allele fixed depends on the initial frequencies WAA > WAa > Waa Allele A fixed WAA < WAa < Waa Allele A fixed (2) The separative one: {AA} {aa} {Aa}; Formal fitness coefficient W 11(AA), W 12(Aa), W 22(aa)

Fitnesses Outcome WAa > WAA, Waa Stable polymorphic equilibrium with A and a WAa < WAA, Waa Unstable equilibrium, which allele fixed depends on the initial frequencies WAA > WAa > Waa Allele A fixed WAA < WAa < Waa Allele A fixed (3) The Mendel dominant one: {AA, Aa} and {aa}; Formal fitness coefficient W 11(AA)=W 12(Aa), W 22(aa)

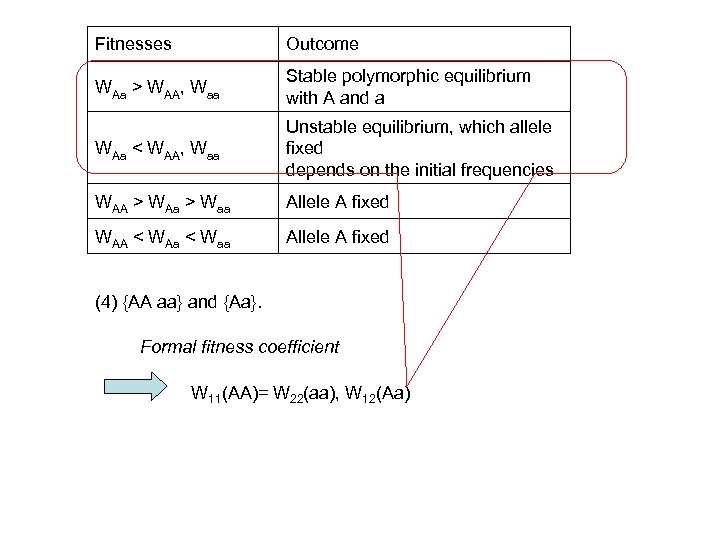Fitnesses Outcome WAa > WAA, Waa Stable polymorphic equilibrium with A and a WAa < WAA, Waa Unstable equilibrium, which allele fixed depends on the initial frequencies WAA > WAa > Waa Allele A fixed WAA < WAa < Waa Allele A fixed (4) {AA aa} and {Aa}. Formal fitness coefficient W 11(AA)= W 22(aa), W 12(Aa)

Phenotype Trait Possible genotypes AA, Aa, aa Possible phenotypes (1) The neutral one, where the only class is {AA, aa, Aa}; Trait: t 1 (2) The separative one: {AA} {aa} {Aa}; Traits: t 1, t 2, t 3 (3) The Mendel dominant one: {AA, Aa} and {aa}; Traits: t 1, t 2. (4) {AA aa} and {Aa}. Traits: t 1, t 2.

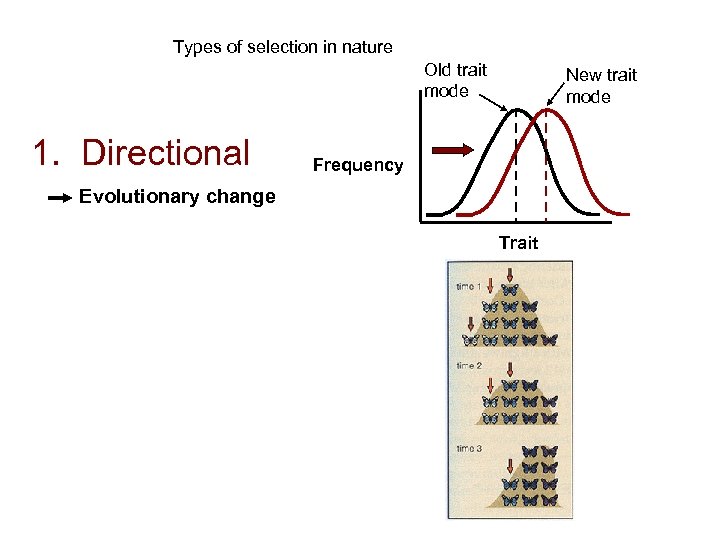Types of selection in nature Old trait mode 1. Directional New trait mode Frequency Evolutionary change Trait

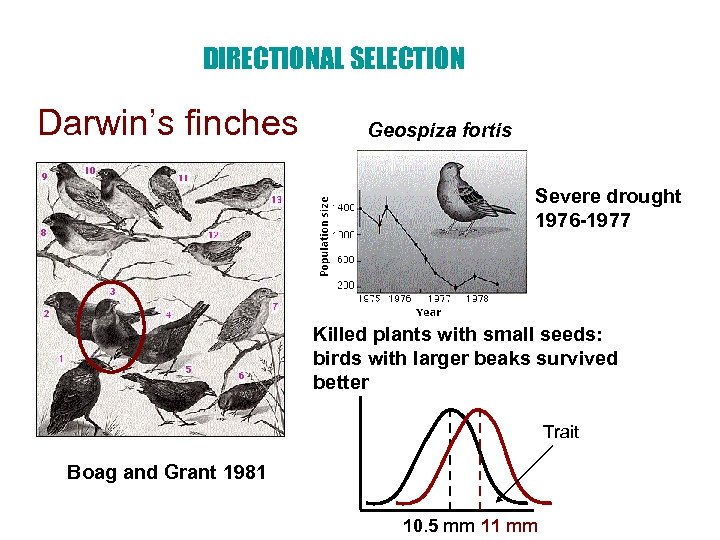DIRECTIONAL SELECTION Darwin’s finches Geospiza fortis Severe drought 1976 -1977 Killed plants with small seeds: birds with larger beaks survived better Trait Boag and Grant 1981 10. 5 mm 11 mm

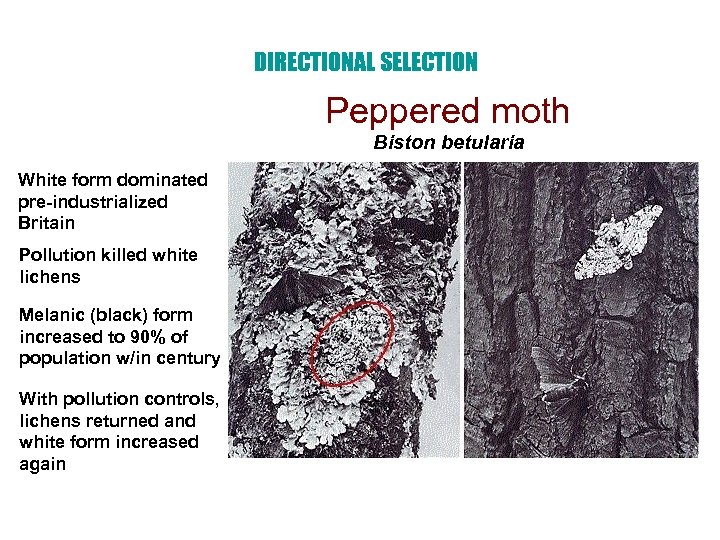DIRECTIONAL SELECTION Peppered moth Biston betularia White form dominated pre-industrialized Britain Pollution killed white lichens Melanic (black) form increased to 90% of population w/in century With pollution controls, lichens returned and white form increased again

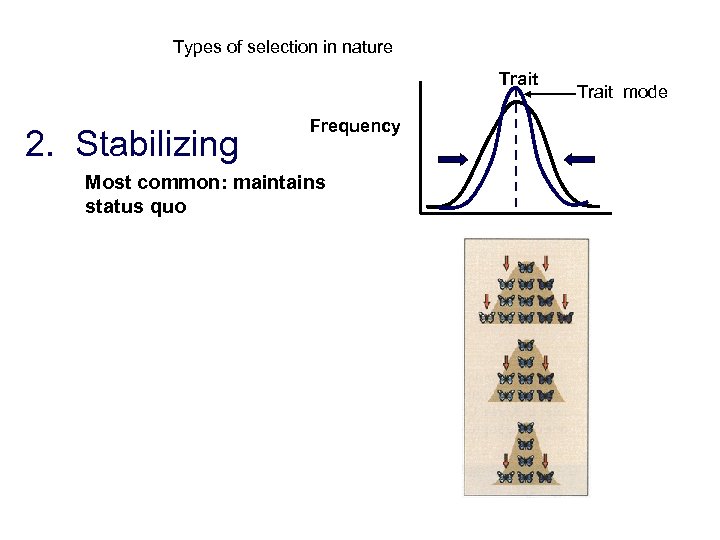Types of selection in nature Trait 2. Stabilizing Frequency Most common: maintains status quo Trait mode

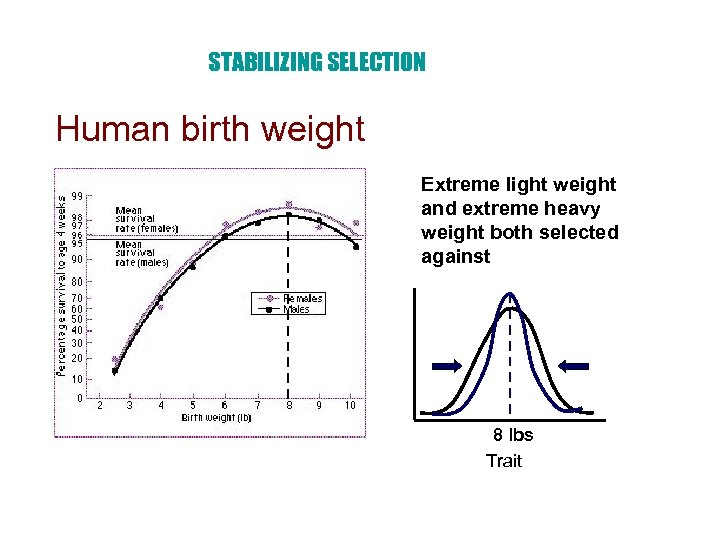STABILIZING SELECTION Human birth weight Extreme light weight and extreme heavy weight both selected against 8 lbs Trait

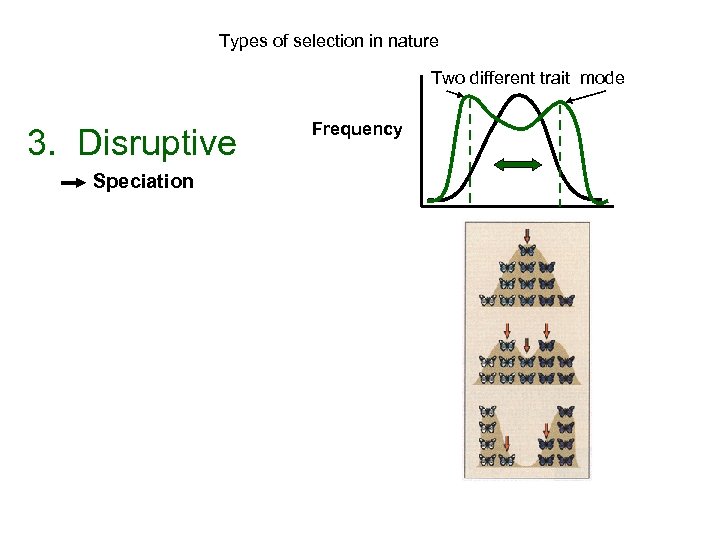Types of selection in nature Two different trait mode 3. Disruptive Speciation Frequency

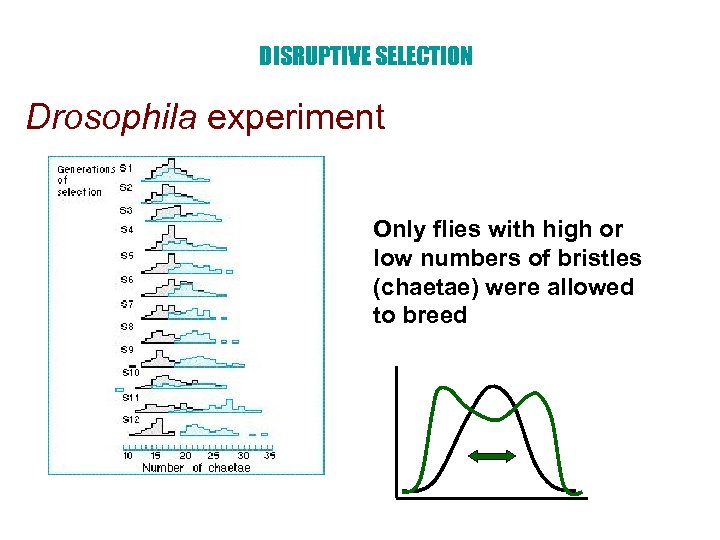DISRUPTIVE SELECTION Drosophila experiment Only flies with high or low numbers of bristles (chaetae) were allowed to breed

Fitness coefficients Alleles A, a Weight (Price) u(A), u(a) Zygote Trait (AA ) 2 u(A) (Aa ) u(A)+u(a) (aa ) 2 u(a) T- optimal value of the trait T

Example for different relations between T, values u() of traits and trajectories

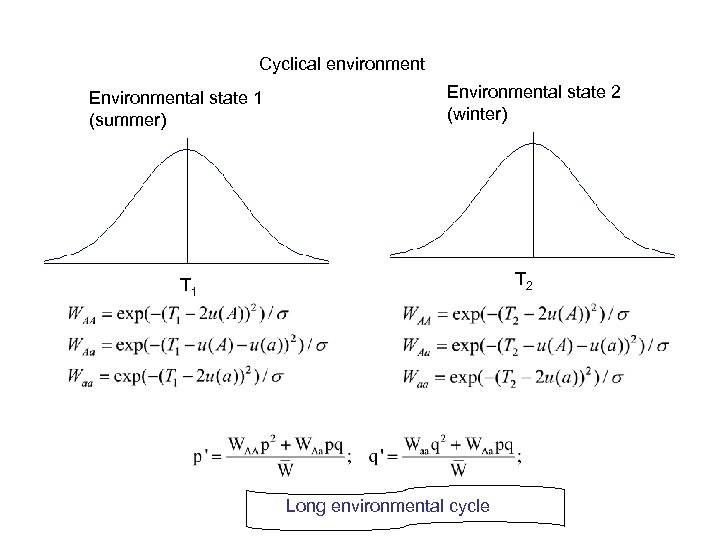Cyclical environment Environmental state 1 (summer) Environmental state 2 (winter) T 2 T 1 Long environmental cycle

Examples trajectories fro cyclical environment in Aa, aa coordinates

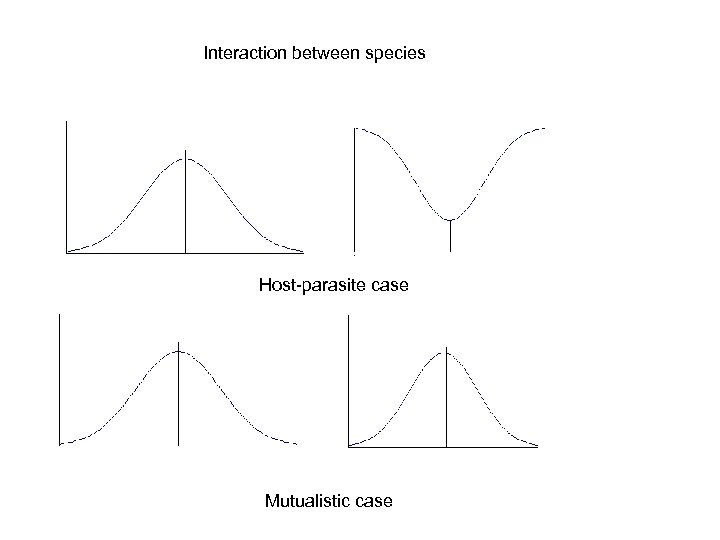Interaction between species Host-parasite case Mutualistic case

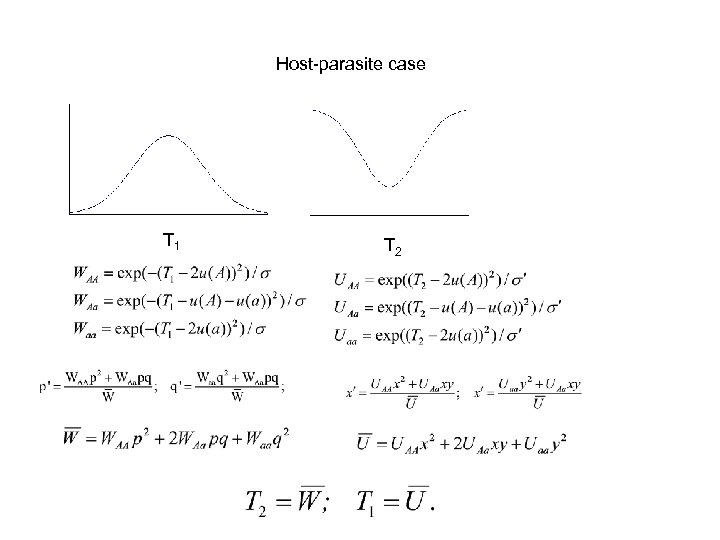Host-parasite case T 1 T 2

Mutualistic case T 1 T 2

Simulation

Frequency depended selection

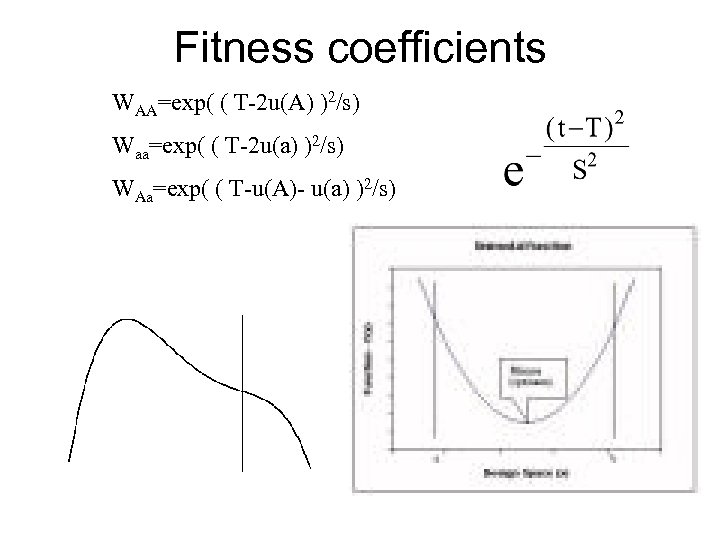Fitness coefficients WAA=exp( ( T-2 u(A) )2/s) Waa=exp( ( T-2 u(a) )2/s) WAa=exp( ( T-u(A)- u(a) )2/s)