95d0d690effdf4a422d8e83798d5f84b.ppt
- Количество слайдов: 39
 Summary § § § NP-hard and NP-completeness proof Polynomial time reduction List of NP-complete problems Knapsack problem Isomprphisim is an open problem, network flow problem where capacities are nodes, node capacity reduced to edge capacity problem. 1
Summary § § § NP-hard and NP-completeness proof Polynomial time reduction List of NP-complete problems Knapsack problem Isomprphisim is an open problem, network flow problem where capacities are nodes, node capacity reduced to edge capacity problem. 1
 Reduction-1 § § § § § Isomorphism is an open problem. Network flow problem where capacities are nodes, node capacity reduced to edge capacity problem. Polynomial Prbl. Reduction from independent set to a recipe. IS to (node cover) VC. Example of nodes and edges. . Traffic police VC(G, k) {G(V, E), k}, is there a node cover of size k, that touches every edge, every edge touches one of the nodes, IS, no two nodes in that subset are adjacent. IS VC. Idea is IS->[convert]->[solver for VC]->? Question if there is an independent set IS of G, size k ? This means if there is a VC of size k, (G, k) [IS]->(G’, k’) [VC]-> (G, k) [IS] [VC] how to do (G, k) [G=G’, k k’ = n-k] [VC] (G, k) [IS] reduction [VC] I have to issue a theorem Theorem: A subset of nodes S is a nodecover iff V-S is an independent set. 2 IS {G, k} given in to the box of VC
Reduction-1 § § § § § Isomorphism is an open problem. Network flow problem where capacities are nodes, node capacity reduced to edge capacity problem. Polynomial Prbl. Reduction from independent set to a recipe. IS to (node cover) VC. Example of nodes and edges. . Traffic police VC(G, k) {G(V, E), k}, is there a node cover of size k, that touches every edge, every edge touches one of the nodes, IS, no two nodes in that subset are adjacent. IS VC. Idea is IS->[convert]->[solver for VC]->? Question if there is an independent set IS of G, size k ? This means if there is a VC of size k, (G, k) [IS]->(G’, k’) [VC]-> (G, k) [IS] [VC] how to do (G, k) [G=G’, k k’ = n-k] [VC] (G, k) [IS] reduction [VC] I have to issue a theorem Theorem: A subset of nodes S is a nodecover iff V-S is an independent set. 2 IS {G, k} given in to the box of VC
 p Reduction takes polytime § IS {G, k} given in to the box of VC Reduction runs in polytime at the worst case, any instance of IS, reduced to VC, by, g=g’, k’=n-k, (one clock time). . § IS p VC § The otherway around is not always true in general. § § § § § Question 1? If X p Y and if Y has a polytime solution, does X has a polytime solution? . . Proof: Poly of Poly is poly. . O(p'(|s|))+p(|s|) O(p) bounded by a poly solution for X. Question 2? If X p Y and if X does not have a polytime solution (cannot be solved with a polytime question), does Y has a polytime solution? . . Cannot Poly of Poly is poly. . O(p'(b|s|)+p(|s|) O(b|s|) solution. Clauses related together by ANDS. . (x 1 v x 2) ^ ( x 1 v x 3) ^ (x 2 v x 3) how to satisfy this. Not all can be made true, example (x 2 ) ^ ( x 2) The maximum number of literals in a clause determines k-sat. Example 3 -sat at most 3 literals. 2 -sat at most 2 literals. . 3 sat p IS 3
p Reduction takes polytime § IS {G, k} given in to the box of VC Reduction runs in polytime at the worst case, any instance of IS, reduced to VC, by, g=g’, k’=n-k, (one clock time). . § IS p VC § The otherway around is not always true in general. § § § § § Question 1? If X p Y and if Y has a polytime solution, does X has a polytime solution? . . Proof: Poly of Poly is poly. . O(p'(|s|))+p(|s|) O(p) bounded by a poly solution for X. Question 2? If X p Y and if X does not have a polytime solution (cannot be solved with a polytime question), does Y has a polytime solution? . . Cannot Poly of Poly is poly. . O(p'(b|s|)+p(|s|) O(b|s|) solution. Clauses related together by ANDS. . (x 1 v x 2) ^ ( x 1 v x 3) ^ (x 2 v x 3) how to satisfy this. Not all can be made true, example (x 2 ) ^ ( x 2) The maximum number of literals in a clause determines k-sat. Example 3 -sat at most 3 literals. 2 -sat at most 2 literals. . 3 sat p IS 3
 p Reduction takes polytime § § § 3 sat p IS A boolean formula 3 sat reducer input for IS (G, k) IS If formula is satisfiable then there is an IS. Tree boxes, , input, X, Reducer and Y solver-output yes or no. Decision YES OR NO 4
p Reduction takes polytime § § § 3 sat p IS A boolean formula 3 sat reducer input for IS (G, k) IS If formula is satisfiable then there is an IS. Tree boxes, , input, X, Reducer and Y solver-output yes or no. Decision YES OR NO 4
 3 -SAT p IS - Reduction in polytime § A boolean formula 3 -SAT reducer input for IS (G, k) IS § If formula is satisfiable then there is an IS. § Tree boxes, input, X, Reducer and Y solver-output yes or no. Decision YES OR NO § If y runs in polytime, and result will be ploy of poly(|x|). § If there is no poly solver for X, X reduced to Y, then there cannot be a polysolver for Y. § § § § 3 -SAT p IS no two nodes adjacent. (x 1, x 2, x 3)^( x 1, x 4, x 5)^(x 1, x 2, x 4)^(x 3, x 4, x 5) At least one of literals must be true, Satisfying this formula definitely corresponds to an IS, with size equal to number of clauses. . Question make clauses true. . Conversely if there is an independent set, then formula must be true, that means there must be at least one literal to be true. 3 -SAT although seems straight forward but presently we don’t know an algorithm to solve it in polytime algorithm. . 5
3 -SAT p IS - Reduction in polytime § A boolean formula 3 -SAT reducer input for IS (G, k) IS § If formula is satisfiable then there is an IS. § Tree boxes, input, X, Reducer and Y solver-output yes or no. Decision YES OR NO § If y runs in polytime, and result will be ploy of poly(|x|). § If there is no poly solver for X, X reduced to Y, then there cannot be a polysolver for Y. § § § § 3 -SAT p IS no two nodes adjacent. (x 1, x 2, x 3)^( x 1, x 4, x 5)^(x 1, x 2, x 4)^(x 3, x 4, x 5) At least one of literals must be true, Satisfying this formula definitely corresponds to an IS, with size equal to number of clauses. . Question make clauses true. . Conversely if there is an independent set, then formula must be true, that means there must be at least one literal to be true. 3 -SAT although seems straight forward but presently we don’t know an algorithm to solve it in polytime algorithm. . 5
 Class of NP problems § § § Def: A Decision Prbl X is associated with a set of strings or input, to a problem X {language}, such that x X. Def: An algorithm A, solves prbl x, iff A(x) says yes iff x X. Def: If A runs in O(p|x|), for some polyn function p, then all X is poly solvable. P: poly time solvable. Network flow, that is not a decision question. Maximize flow. Decision question would if there is a flow less than some value ie 20, yes or no. For 3 -SAT we don’t know yet if it is in NP, 3 sat, since we don’t know yet if there is a polynomial time to solve 3 sat. CHECKING Verifying. If an input is in the language or not. {Instance, [certificate, witness proof, hint] f} ->[B: X checker algorithm A, polytime]->. . 6
Class of NP problems § § § Def: A Decision Prbl X is associated with a set of strings or input, to a problem X {language}, such that x X. Def: An algorithm A, solves prbl x, iff A(x) says yes iff x X. Def: If A runs in O(p|x|), for some polyn function p, then all X is poly solvable. P: poly time solvable. Network flow, that is not a decision question. Maximize flow. Decision question would if there is a flow less than some value ie 20, yes or no. For 3 -SAT we don’t know yet if it is in NP, 3 sat, since we don’t know yet if there is a polynomial time to solve 3 sat. CHECKING Verifying. If an input is in the language or not. {Instance, [certificate, witness proof, hint] f} ->[B: X checker algorithm A, polytime]->. . 6
 Def: B is an efficient certifier for language X, if § § 1) B is a polytime algorithm with respect to its inputs x, t. outputs yes or no, 2) exists a polyfunct p, such that for any input x X (target, k of IS), iff some x in language X, certificate C (bounded by a polynomial program size!), witness, |t|. p(|t|). and B(x, t) = yes. § NP is the class of problems that have efficient certifiers: B as given above. § X is in NP iff there is an efficient certifier for X. § ie for VC reduces to IS and IS reduces to VC, but certifier is SAT, the instances of problem G and k, there exists a program t, and a B(x, t), x=(G, k), t is a subset of nodes which is VC of G, size k, if there is one, and B(xm t), check whether this subset is actually a nodecover of G. 7
Def: B is an efficient certifier for language X, if § § 1) B is a polytime algorithm with respect to its inputs x, t. outputs yes or no, 2) exists a polyfunct p, such that for any input x X (target, k of IS), iff some x in language X, certificate C (bounded by a polynomial program size!), witness, |t|. p(|t|). and B(x, t) = yes. § NP is the class of problems that have efficient certifiers: B as given above. § X is in NP iff there is an efficient certifier for X. § ie for VC reduces to IS and IS reduces to VC, but certifier is SAT, the instances of problem G and k, there exists a program t, and a B(x, t), x=(G, k), t is a subset of nodes which is VC of G, size k, if there is one, and B(xm t), check whether this subset is actually a nodecover of G. 7
 § § ie for VC reduces to IS and IS reduces to VC, but certifier is SAT, the instances of problem G and k, there exists a program t, and a B(x, t), x=(G, k), t is a subset of nodes which is VC of G, size k, if there is one, and B(xm t), check whether this subset is actually a nodecover of G. Algorithm checker is simple, checks the size of proposed nodes smaller than k, and checks if these nodes are actually are nodecover, VC. If so it says yes. All these takes polynomial time. If input size is n, total time is n 2. Yes. Otherwise it outputs “not verified”. . No!. To be in NP, Checker checks if proposed solution is a solution. May be a list or other constraints. P NP. . Because all X P. X can be certified (instance ans A(t, x)) in the order of a poly-operations but no need since easy to compute. There can never be a NO since solver solves the problem In polytime, easily. P NP. . is a basic elementary fact. 8
§ § ie for VC reduces to IS and IS reduces to VC, but certifier is SAT, the instances of problem G and k, there exists a program t, and a B(x, t), x=(G, k), t is a subset of nodes which is VC of G, size k, if there is one, and B(xm t), check whether this subset is actually a nodecover of G. Algorithm checker is simple, checks the size of proposed nodes smaller than k, and checks if these nodes are actually are nodecover, VC. If so it says yes. All these takes polynomial time. If input size is n, total time is n 2. Yes. Otherwise it outputs “not verified”. . No!. To be in NP, Checker checks if proposed solution is a solution. May be a list or other constraints. P NP. . Because all X P. X can be certified (instance ans A(t, x)) in the order of a poly-operations but no need since easy to compute. There can never be a NO since solver solves the problem In polytime, easily. P NP. . is a basic elementary fact. 8
 NP-hard and NP-complete Def: Problem X is NP-C if 1. 2. X NP For any Y NP, Y p X with a diagram, y [Y] [Y p X ] x [solver for X poly solver] yes or no |x|=|y| Every known reduces to unknown. Consequence of this is Corollary if at least one NPC problem X is in P (runs in polynomial time): then NP=P. Even one problem X is X NP (1), P is already contained on NP, P NP, this would mean NP P From second statement and diagram (2), that is running in polytime. The words swapping. . Then the roof of NP is collapsing into P. Equivalently if P NP, then no any NPC is in P. Therefore if X is NPC, there can be no polynomial time solution for problem X. 9
NP-hard and NP-complete Def: Problem X is NP-C if 1. 2. X NP For any Y NP, Y p X with a diagram, y [Y] [Y p X ] x [solver for X poly solver] yes or no |x|=|y| Every known reduces to unknown. Consequence of this is Corollary if at least one NPC problem X is in P (runs in polynomial time): then NP=P. Even one problem X is X NP (1), P is already contained on NP, P NP, this would mean NP P From second statement and diagram (2), that is running in polytime. The words swapping. . Then the roof of NP is collapsing into P. Equivalently if P NP, then no any NPC is in P. Therefore if X is NPC, there can be no polynomial time solution for problem X. 9
 NP-hard and NP-complete Then the roof of NP is collapsing into P. Equivalently if P NP, then no any NPC is in P. Therefore if X is NPC, there can be no polynomial time solution for problem X. There were not NPC classified problems, Cooks’s theorem Satisfiabilility. . tedious to prove but tractable. . Levin. Then how to establish other problems are npc, Poly reduction of Y to X, and show X is in NP. IF X is known to be NPC, we can proove Y to be NPC by show by a polytime reduction of instances of X to instances of Y. Poly of poly, . For each NP problem there is a poly reduction to X and from X to Y, (by transitivity every problem in NP reduces to Y) Problem X is called NP-hard, not the first part but the second part is satisfied, in other words, if every problem in NP reduces to X in ploytime. 10
NP-hard and NP-complete Then the roof of NP is collapsing into P. Equivalently if P NP, then no any NPC is in P. Therefore if X is NPC, there can be no polynomial time solution for problem X. There were not NPC classified problems, Cooks’s theorem Satisfiabilility. . tedious to prove but tractable. . Levin. Then how to establish other problems are npc, Poly reduction of Y to X, and show X is in NP. IF X is known to be NPC, we can proove Y to be NPC by show by a polytime reduction of instances of X to instances of Y. Poly of poly, . For each NP problem there is a poly reduction to X and from X to Y, (by transitivity every problem in NP reduces to Y) Problem X is called NP-hard, not the first part but the second part is satisfied, in other words, if every problem in NP reduces to X in ploytime. 10
 n n n From www. ece. mtu. edu/faculty/shiyan/EE 590 0 Spring 10/NP-complete. ppt www. cs. dartmouth. edu/~ac/Teach/CS 3 9 Winter 09/Slides. And. Notes/lec 28 npcom plete. pdf
n n n From www. ece. mtu. edu/faculty/shiyan/EE 590 0 Spring 10/NP-complete. ppt www. cs. dartmouth. edu/~ac/Teach/CS 3 9 Winter 09/Slides. And. Notes/lec 28 npcom plete. pdf
 Nondeterministic algorithms n n n A nondeterminstic algorithm consists of phase 1: guessing phase 2: checking If the checking stage of a nondeterministic algorithm is of polynomial time-complexity, then this algorithm is called an NP (nondeterministic polynomial) algorithm. NP problems : n e. g. searching, MST sorting satisfiability problem (SAT) traveling salesperson problem (TSP) 12
Nondeterministic algorithms n n n A nondeterminstic algorithm consists of phase 1: guessing phase 2: checking If the checking stage of a nondeterministic algorithm is of polynomial time-complexity, then this algorithm is called an NP (nondeterministic polynomial) algorithm. NP problems : n e. g. searching, MST sorting satisfiability problem (SAT) traveling salesperson problem (TSP) 12
 Nondeterministic searching algorithm n n n Search for x in an array A Choice(S) : arbitrarily chooses one of the elements in set S Failure : an unsuccessful completion Success : a successful completion Nonderministic searching algorithm: j ← choice(1 : n) /* guessing */ if A(j) = x then success /* checking */ else failure 13
Nondeterministic searching algorithm n n n Search for x in an array A Choice(S) : arbitrarily chooses one of the elements in set S Failure : an unsuccessful completion Success : a successful completion Nonderministic searching algorithm: j ← choice(1 : n) /* guessing */ if A(j) = x then success /* checking */ else failure 13
 n n A nondeterministic algorithm terminates unsuccessfully iff there exist not a set of choices leading to a success signal. A deterministic interpretation of a nondeterministic algorithm can be made by allowing unbounded parallelism in computation. The runtime required for choice(1 : n) is O(1). The runtime for nondeterministic searching algorithm is also O(1) 14
n n A nondeterministic algorithm terminates unsuccessfully iff there exist not a set of choices leading to a success signal. A deterministic interpretation of a nondeterministic algorithm can be made by allowing unbounded parallelism in computation. The runtime required for choice(1 : n) is O(1). The runtime for nondeterministic searching algorithm is also O(1) 14
 Nondeterministic sorting B← 0 /* guessing */ for i = 1 to n do j ← choice(1 : n) if B[j] ≠ 0 then failure B[j] = A[i] /* checking */ for i = 1 to n-1 do if B[i] > B[i+1] then failure success 15
Nondeterministic sorting B← 0 /* guessing */ for i = 1 to n do j ← choice(1 : n) if B[j] ≠ 0 then failure B[j] = A[i] /* checking */ for i = 1 to n-1 do if B[i] > B[i+1] then failure success 15
 n n NP : the class of decision problem which can be solved by a non-deterministic polynomial algorithm. P: the class of problems which can be solved by a deterministic polynomial algorithm. NP-hard: the class of problems to which every NP problem reduces. NP-complete (NPC): the class of problems which are NP-hard and belong to NP. 16
n n NP : the class of decision problem which can be solved by a non-deterministic polynomial algorithm. P: the class of problems which can be solved by a deterministic polynomial algorithm. NP-hard: the class of problems to which every NP problem reduces. NP-complete (NPC): the class of problems which are NP-hard and belong to NP. 16
 Some concepts of NPC n n n Definition of reduction: Problem A reduces to problem B (A B) iff A can be solved by a deterministic polynomial time algorithm using a deterministic algorithm that solves B in polynomial time. B is harder. Up to now, none of the NPC problems can be solved by a deterministic polynomial time algorithm in the worst case. It does not seem to have any polynomial time algorithm to solve the NPC problems. 17
Some concepts of NPC n n n Definition of reduction: Problem A reduces to problem B (A B) iff A can be solved by a deterministic polynomial time algorithm using a deterministic algorithm that solves B in polynomial time. B is harder. Up to now, none of the NPC problems can be solved by a deterministic polynomial time algorithm in the worst case. It does not seem to have any polynomial time algorithm to solve the NPC problems. 17
 n The theory of NP-completeness always considers the worst case. The lower bound of any NPC problem seems to be in the order of an exponential function. Not all NP problems are difficult. (e. g. the MST problem is an NP problem. ) If A, B NPC, then A B and B A. n Theory of NP-completeness n n n If any NPC problem can be solved in polynomial time, then all NP problems can be solved in polynomial time. (NP = P) 18
n The theory of NP-completeness always considers the worst case. The lower bound of any NPC problem seems to be in the order of an exponential function. Not all NP problems are difficult. (e. g. the MST problem is an NP problem. ) If A, B NPC, then A B and B A. n Theory of NP-completeness n n n If any NPC problem can be solved in polynomial time, then all NP problems can be solved in polynomial time. (NP = P) 18
 Decision problems n n n The solution is simply “Yes” or “No”. Optimization problems are more difficult. e. g. the traveling salesperson problem n n Optimization version: Find the shortest tour Decision version: Is there a tour whose total length is less than or equal to a constant c ? 19
Decision problems n n n The solution is simply “Yes” or “No”. Optimization problems are more difficult. e. g. the traveling salesperson problem n n Optimization version: Find the shortest tour Decision version: Is there a tour whose total length is less than or equal to a constant c ? 19
 Solving an optimization problem by a decision algorithm : n Solving TSP optimization problem by decision algorithm : n n Give c 1 and test (decision algorithm) Give c 2 and test (decision algorithm) Give cn and test (decision algorithm) We can find the smallest ci 20
Solving an optimization problem by a decision algorithm : n Solving TSP optimization problem by decision algorithm : n n Give c 1 and test (decision algorithm) Give c 2 and test (decision algorithm) Give cn and test (decision algorithm) We can find the smallest ci 20
 The satisfiability problem n The satisfiability problem: Given a Boolean statement, determine whether it is satisfiable or not. n The logical formula : n n DNF, CNF, literals and clause. Conjunctive nrml form If there is at least one assignment which satisfies a formula in DNF, then we say that this formula is satisfiable; otherwise, it is unsatisfiable. n n x 1 v x 2 v x 3 x 1 & x 2 & x 3 (F, F, T) will make statement true (satisfied) or (-x 1, -x 2 , x 3) Unsatisfiable: n (x 1 v x 2) & (x 1 v -x 2) & (-x 1 v -x 2) 21
The satisfiability problem n The satisfiability problem: Given a Boolean statement, determine whether it is satisfiable or not. n The logical formula : n n DNF, CNF, literals and clause. Conjunctive nrml form If there is at least one assignment which satisfies a formula in DNF, then we say that this formula is satisfiable; otherwise, it is unsatisfiable. n n x 1 v x 2 v x 3 x 1 & x 2 & x 3 (F, F, T) will make statement true (satisfied) or (-x 1, -x 2 , x 3) Unsatisfiable: n (x 1 v x 2) & (x 1 v -x 2) & (-x 1 v -x 2) 21
 Cook’s theorem n n n NP = P iff the satisfiability problem is a P problem. SAT is NP-complete. It is the first NP-complete problem. Every NP problem reduces to SAT. 22
Cook’s theorem n n n NP = P iff the satisfiability problem is a P problem. SAT is NP-complete. It is the first NP-complete problem. Every NP problem reduces to SAT. 22
 Toward NP-Completeness n n Once we have found an NP-complete problem, proving that other problems are also NP-complete becomes easier. Given a new problem Y, it is sufficient to prove that Cook’s problem, or any other NP-complete problems, is polynomially reducible to Y. Known problem -> unknown problem Reduction here is from unknown to every known prbl. 23
Toward NP-Completeness n n Once we have found an NP-complete problem, proving that other problems are also NP-complete becomes easier. Given a new problem Y, it is sufficient to prove that Cook’s problem, or any other NP-complete problems, is polynomially reducible to Y. Known problem -> unknown problem Reduction here is from unknown to every known prbl. 23
 NP-Completeness Proof Assume that CLIQUE problem is NP-complete, to prove that vertex cover (VC) problem is NP-complete. Definition: q A vertex cover of G=(V, E) is V’ V such that every edge in E is incident to some v V’. n Vertex Cover(VC): Given undirected G=(V, E) and integer k, does G have a vertex cover with k vertices? n CLIQUE: Does G contain a clique of size k? 24
NP-Completeness Proof Assume that CLIQUE problem is NP-complete, to prove that vertex cover (VC) problem is NP-complete. Definition: q A vertex cover of G=(V, E) is V’ V such that every edge in E is incident to some v V’. n Vertex Cover(VC): Given undirected G=(V, E) and integer k, does G have a vertex cover with k vertices? n CLIQUE: Does G contain a clique of size k? 24
 NP-Completeness Proof: Vertex Cover(VC) n n n Problem: Given undirected G=(V, E) and integer k, does G have a vertex cover with k vertices? Theorem: the VC problem is NP-complete. Proof: (Reduction from CLIQUE) n VC is in NP. This is trivial since we can check it easily in polynomial time. n Goal: Transform arbitrary CLIQUE instance into VC instance such that CLIQUE answer is “yes” iff VC answer is “yes”. 25
NP-Completeness Proof: Vertex Cover(VC) n n n Problem: Given undirected G=(V, E) and integer k, does G have a vertex cover with k vertices? Theorem: the VC problem is NP-complete. Proof: (Reduction from CLIQUE) n VC is in NP. This is trivial since we can check it easily in polynomial time. n Goal: Transform arbitrary CLIQUE instance into VC instance such that CLIQUE answer is “yes” iff VC answer is “yes”. 25
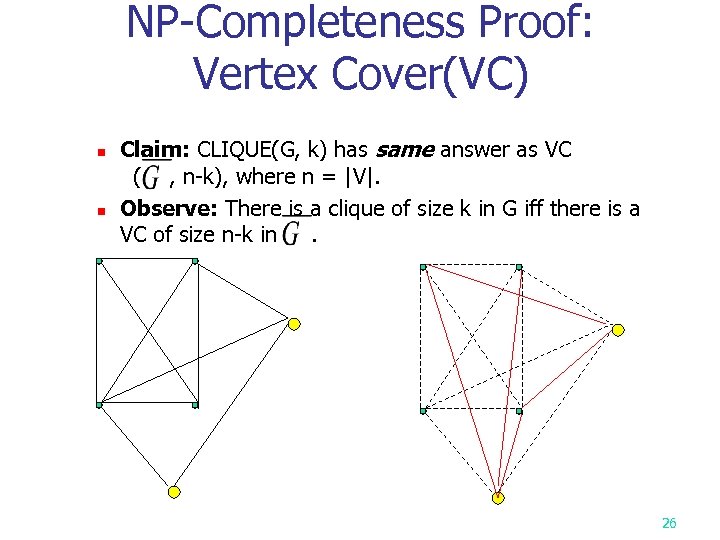 NP-Completeness Proof: Vertex Cover(VC) n n Claim: CLIQUE(G, k) has same answer as VC ( , n-k), where n = |V|. Observe: There is a clique of size k in G iff there is a VC of size n-k in. 26
NP-Completeness Proof: Vertex Cover(VC) n n Claim: CLIQUE(G, k) has same answer as VC ( , n-k), where n = |V|. Observe: There is a clique of size k in G iff there is a VC of size n-k in. 26
 NP-Completeness Proof: Vertex Cover(VC) n n Observe: If D is a VC in , then has no edge between vertices in V-D. So, we have k-clique in G n-k VC in Can transform in polynomial time. 27
NP-Completeness Proof: Vertex Cover(VC) n n Observe: If D is a VC in , then has no edge between vertices in V-D. So, we have k-clique in G n-k VC in Can transform in polynomial time. 27
 NP-Completeness Proof: CLIQUE n n Assume that SAT problem is NP-complete, to prove that CLIQUE problem is NP-complete Problem: Does G=(V, E) contain a clique of size k? Theorem: Clique is NP-Complete. (reduction from SAT) Idea: Make “column” for each of k clauses. n No edge within a column. n All other edges present except between x and x’ 28
NP-Completeness Proof: CLIQUE n n Assume that SAT problem is NP-complete, to prove that CLIQUE problem is NP-complete Problem: Does G=(V, E) contain a clique of size k? Theorem: Clique is NP-Complete. (reduction from SAT) Idea: Make “column” for each of k clauses. n No edge within a column. n All other edges present except between x and x’ 28
 NP-Completeness Proof: CLIQUE n Example: G= n G has m-clique (m is the number of clauses in E), iff E is satisfiable. (Assign value 1 to all variables in clique) 29
NP-Completeness Proof: CLIQUE n Example: G= n G has m-clique (m is the number of clauses in E), iff E is satisfiable. (Assign value 1 to all variables in clique) 29
 Graph coloring problem n n Def: A coloring of a graph G=(V, E) is a function f : V { 1, 2, 3, …, k } such that if (u, v) E, then f(u) f(v). The graph coloring problem is to determine if G has a coloring for k. E. g. 3 -colorable f(a)=1, f(b)=2, f(c)=1 f(d)=2, f(e)=3 30
Graph coloring problem n n Def: A coloring of a graph G=(V, E) is a function f : V { 1, 2, 3, …, k } such that if (u, v) E, then f(u) f(v). The graph coloring problem is to determine if G has a coloring for k. E. g. 3 -colorable f(a)=1, f(b)=2, f(c)=1 f(d)=2, f(e)=3 30
 Set cover problem n Def: F = {Si} = { S 1, S 2, …, Sk } Si = { u 1, u 2, …, un } T is a set cover of F if T F and Si = Si The set cover decision problem is to determine if F has a cover T containing no more than c sets. n Example F = {(a 1, a 3), (a 2, a 4), (a 2, a 3), (a 4), (a 1, a 3 , a 4)} s 1 s 2 s 3 s 4 s 5 T = { s 1, s 3, s 4 } set cover 31
Set cover problem n Def: F = {Si} = { S 1, S 2, …, Sk } Si = { u 1, u 2, …, un } T is a set cover of F if T F and Si = Si The set cover decision problem is to determine if F has a cover T containing no more than c sets. n Example F = {(a 1, a 3), (a 2, a 4), (a 2, a 3), (a 4), (a 1, a 3 , a 4)} s 1 s 2 s 3 s 4 s 5 T = { s 1, s 3, s 4 } set cover 31
 Subset sum problem n n Def: A set of positive numbers A = { a 1, a 2, …, an } a constant C Determine if A A s. t. ai = C e. g. A = { 7, 5, 19, 1, 12, 8, 14 } n n C = 21, A = { 7, 14 } C = 11, no solution 32
Subset sum problem n n Def: A set of positive numbers A = { a 1, a 2, …, an } a constant C Determine if A A s. t. ai = C e. g. A = { 7, 5, 19, 1, 12, 8, 14 } n n C = 21, A = { 7, 14 } C = 11, no solution 32
 Partition problem n Def: Given a set of positive numbers A = { a 1, a 2, …, an }, determine if a partition P, s. t. ai = ai i p n i p e. g. A = {3, 6, 1, 9, 4, 11} partition : {3, 1, 9, 4} and {6, 11} 33
Partition problem n Def: Given a set of positive numbers A = { a 1, a 2, …, an }, determine if a partition P, s. t. ai = ai i p n i p e. g. A = {3, 6, 1, 9, 4, 11} partition : {3, 1, 9, 4} and {6, 11} 33
 Bin packing problem n Def: n items, each of size ci , ci > 0 n bin capacity : C Determine if we can assign the items into k bins, s. t. ci C , 1 j k. i binj 34
Bin packing problem n Def: n items, each of size ci , ci > 0 n bin capacity : C Determine if we can assign the items into k bins, s. t. ci C , 1 j k. i binj 34
 Hamiltonian cycle problem n n Def: A Hamiltonian cycle is a round trip path along n edges of G which visits every vertex once and returns to its starting vertex. e. g. Hamiltonian cycle : 1, 2, 8, 7, 6, 5, 4, 3, 1. 35
Hamiltonian cycle problem n n Def: A Hamiltonian cycle is a round trip path along n edges of G which visits every vertex once and returns to its starting vertex. e. g. Hamiltonian cycle : 1, 2, 8, 7, 6, 5, 4, 3, 1. 35
 Traveling salesperson problem n Def: A tour of a directed graph G=(V, E) is a directed cycle that includes every vertex in V. The problem is to find a tour of minimum cost. 36
Traveling salesperson problem n Def: A tour of a directed graph G=(V, E) is a directed cycle that includes every vertex in V. The problem is to find a tour of minimum cost. 36
 0/1 knapsack problem n Def: n objects, each with a weight wi > 0 a profit pi > 0 capacity of knapsack : M Maximize pixi 1 i n Subject to wixi M 1 i n n xi = 0 or 1, 1 i n Decision version : Given K, pixi K ? 1 i n n Knapsack problem : 0 xi 1, 1 i n. 37
0/1 knapsack problem n Def: n objects, each with a weight wi > 0 a profit pi > 0 capacity of knapsack : M Maximize pixi 1 i n Subject to wixi M 1 i n n xi = 0 or 1, 1 i n Decision version : Given K, pixi K ? 1 i n n Knapsack problem : 0 xi 1, 1 i n. 37
 Subset sum problem § Reduce from 3 SAT problem to show that subset sum problem is NP-complete. 38
Subset sum problem § Reduce from 3 SAT problem to show that subset sum problem is NP-complete. 38
 Three dimensional matching problem § Reduce from 3 SAT problem to show that three dimensional matching (3 DM) problem is NP-complete. 39
Three dimensional matching problem § Reduce from 3 SAT problem to show that three dimensional matching (3 DM) problem is NP-complete. 39


