Сумма и разность n -степеней Вспомним известные

Сумма и разность n -степеней

Вспомним известные формулы Выведем аналогичную формулу для n=4

Проведем анализ полученных формул n=1 n=2 n=3

Выводы: Правая часть этих формул — произведение разности а — Ь на некоторый многочлен, в структуре многочлена хорошо просматривается определенная закономерность: Ø этот многочлен расположен по убывающим степеням переменной а и возрастающим степеням переменной b; Ø все его коэффициенты равны единице; Ø каждый член многочлена имеет одну и ту же степень, равную степени многочлена; Ø Степень многочлена на 1 меньше степени многочлена в левой части равенства

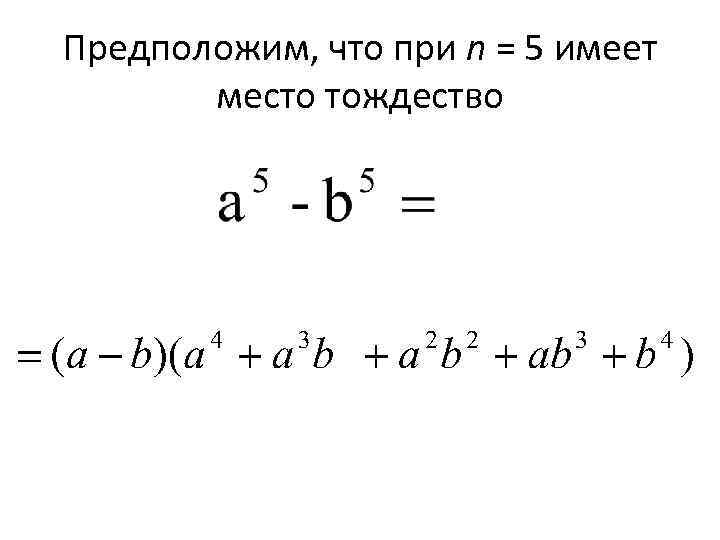Предположим, что при n = 5 имеет место тождество

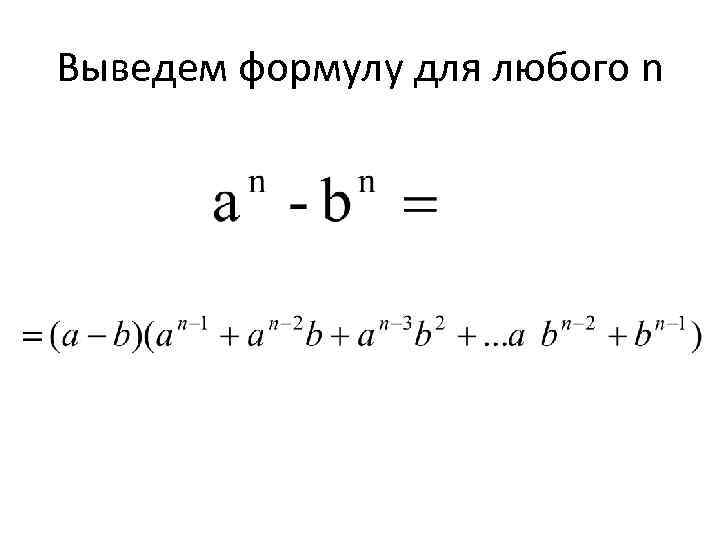Выведем формулу для любого n

Задание 1 Разложите на множители

Задание 2 Разложите на множители

Задание 3 Упростите выражение

Сумма n-степеней • Заметим, что если n- нечетное целое число, тогда Применяя формулу разности n-степеней и заменяя в ней b на –b получим формулу

Сумма n-степеней Чередование знаков

Задание 5 Разложите на множители

Задание 6 Упростите выражение