SUBSKY Efficient Computation of Skylines in Subspaces Authors

SUBSKY: Efficient Computation of Skylines in Subspaces Authors: Yufei Tao, Xiaokui Xiao, and Jian Pei Conference: ICDE 2006 Presenter: Kamiru Superviosr: Dr. Nikos Mamoulis

Skyline Queries § Given a set of d-dimenional points, a point p dominates another p’ if p[i]<=p’[i], for all i in d, and p[j]<p’[j], for any j in d § Skyline queries aim to find the points that are not dominated by any point turnover rate For the NBA database, 1 Low turnover rate and low foul rate are two important factors for a defense player Best point 0 player foul rate 1

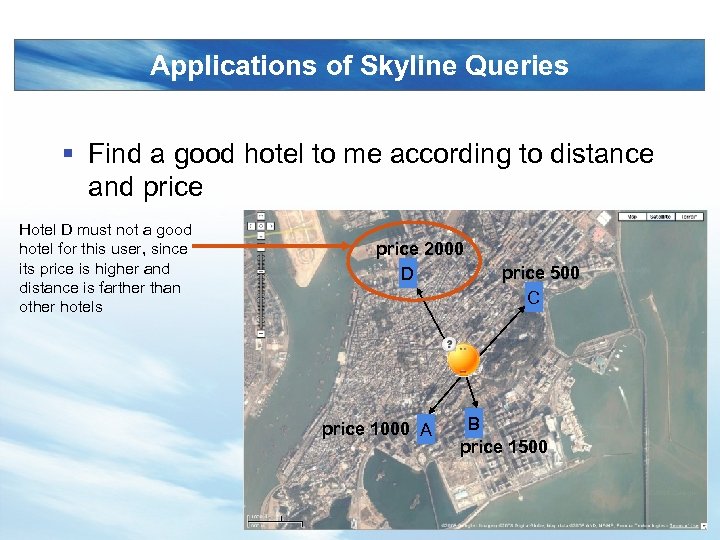
Applications of Skyline Queries § Find a good hotel to me according to distance and price Hotel D must not a good hotel for this user, since its price is higher and distance is farther than other hotels price 2000 D price 1000 A price 500 C B price 1500

Alternative applications of Skyline Queries - i § Some top-k queries are calculated by Skyline queries § A top-k query retrieves the k tuples in P with highest scores according to g § where g must be a monotonic function, ex: g(p) = p. x + p. y

Alternative applications of Skyline Queries - i § Please help me to find who are the top-2 NBA players according to sum of their points and assists in 2007 -2008 season The values are represented by right-top corner of each player photo points The results (up to Jan 23 2008) of this query are 20 Le. Bron Jamesm, 29. 7+7. 4 PRUNED Top-2 results must be in top-2 skyband Allen Iverson, 27+6. 9 assists 10 0 10

Alternative applications of Skyline Queries - ii § Another interesting measurement is dominating count (DC) § DC is counted by the number of dominating points to a query turnover rate Ex: find the top-2 dominating players in the NBA database according to turnover rate and fould rate 1 1 1 4 2 0 Best point 0 player foul rate 1

Skyline Computations § Two categories of skyline computations § § Computing from scratch (no index) Relied on index 1. Computing from scratch (no index) § Advantage • • § No any pre-computation Not to update any index when data changed Drawback • Must calculate from scratch – It must scan the entire data at least once

Skyline Computations 2. Relied on index § § Once you built, get to use it many times Lower query cost is occurred by performing the search on an appropriate structure • • • § B - tree R - tree … Since all of us are database people, (I hope…) we prefer method 2 more

Related works 1. Computing from scratch (no index) § § § Block nested loop Sort filter skyline Divide and conquer Bitmap Linear elimination sort for skyline

Related works 2. Relied on index § B – tree approach • § index R – tree approach • • Nearest neighbor (NN) Branch and bound skyline (BBS) – BBS has been proved that is I/O optimal. It accesses fewer disk pages than any algorithm based on R-trees

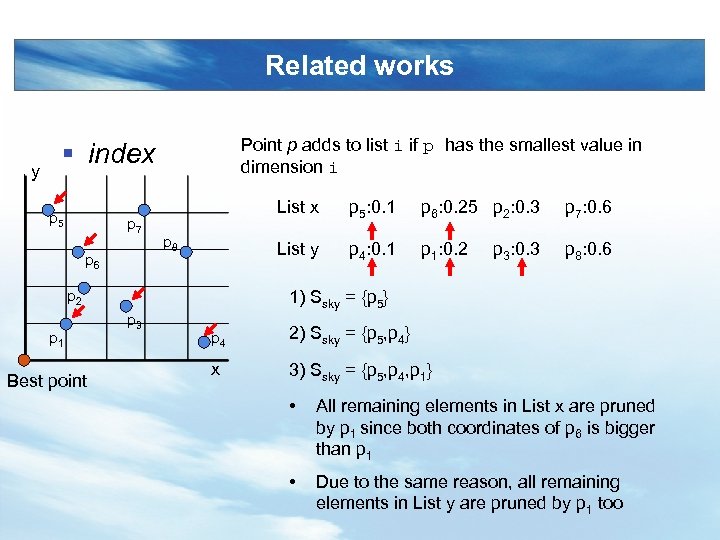
Related works y Point p adds to list i if p has the smallest value in dimension i § index p 5 p 7 p 6 List x p 2 p 1 Best point p 6: 0. 25 p 2: 0. 3 p 7: 0. 6 List y p 8 p 5: 0. 1 p 4: 0. 1 p 1: 0. 2 p 8: 0. 6 p 3: 0. 3 1) Ssky = {p 5} p 3 p 4 2) Ssky = {p 5, p 4} x 3) Ssky = {p 5, p 4, p 1} • All remaining elements in List x are pruned by p 1 since both coordinates of p 6 is bigger than p 1 • Due to the same reason, all remaining elements in List y are pruned by p 1 too

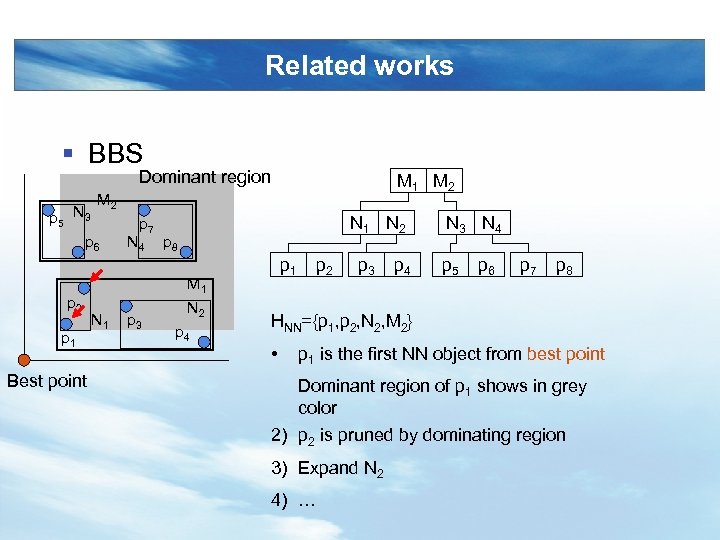
Related works § BBS Dominant region M 1 M 2 M N 3 2 p 5 p 7 p 6 N 4 p 8 p 2 p 1 Best point N 1 p 3 N 1 N 2 M 1 N 2 p 4 p 1 p 2 p 3 p 4 N 3 N 4 p 5 p 6 p 7 p 8 HNN={p 1, p 2, N 2, M 2} • p 1 is the first NN object from best point Dominant region of p 1 shows in grey color 2) p 2 is pruned by dominating region 3) Expand N 2 4) …

SUBSKY § According to NBA database, we have more than 10 different attributes for one player § Skyline queries may be interested in some attributes only

SUBSKY § Build one R-tree and run BBS § BBS is an I/O optimal algorithm based on R-tree index, but their approaches are optimized for a fixed set of dimensions § Build R-trees for all elements in the power set of dimensions § Hugh storage space

SUBSKY for uniform data § Anchor point Ac– the maximal corner of the data space having maximum coordinate on all maximum value of the dimensions 1 y fsky(psky) f(p 1) p 1 coordinate f(p)=max(1 -p[i]), Ac f(p 2) where i is from 1 to d fsky(psky)=min(1 -psky[i]), p 2 where i is from 1 to d psky Pruning region of psky x Best point 1 No any point p satisfying f(p)<fsky(psky) can belong to the skyline A similar result exists for the skyline of any subspace

SUBSKY for uniform data § Skyline queries only apply on relevant dimensions SUB f’sky(psky)=min(1 -psky[i]), where i is in SUB § Then, f(p) < fsky(psky) <= f’sky(psky) § No any point p satisfying the above equation can belong to the skyline

SUBSKY for uniform data x y z f(pi) p 1 0. 2 0. 5 0. 8 p 2 0. 4 0. 9 0. 6 p 3 0. 5 0. 3 0. 1 0. 9 p 4 0. 9 0. 1 0. 6 0. 9 p 5 0. 6 0. 8 0. 7 0. 4 § Assume that our skyline query is interested in dimension x and y only § First, we sort the data by f(pi) § p 3, p 4, p 1, p 2, p 5 § Ssky={p 3}, f’sky(p 3)=0. 5 =min(1 -0. 5, 1 -0. 3) § U=0. 5 (largest f’ value in Ssky) § Ssky={p 3, p 4}, f’sky(p 4)=0. 1 § U=0. 5 § Ssky={p 1, p 4}, f’sky(p 1)=0. 8 § p 3 is removed by adding p 1, since it is dominated by p 1 § U=0. 8

General SUBSKY § In practical, data are usually clustered § If the data are clustered, then we should expect that one anchor point cannot give us enough pruning power 1 Ac A 1 psky x Best point 1

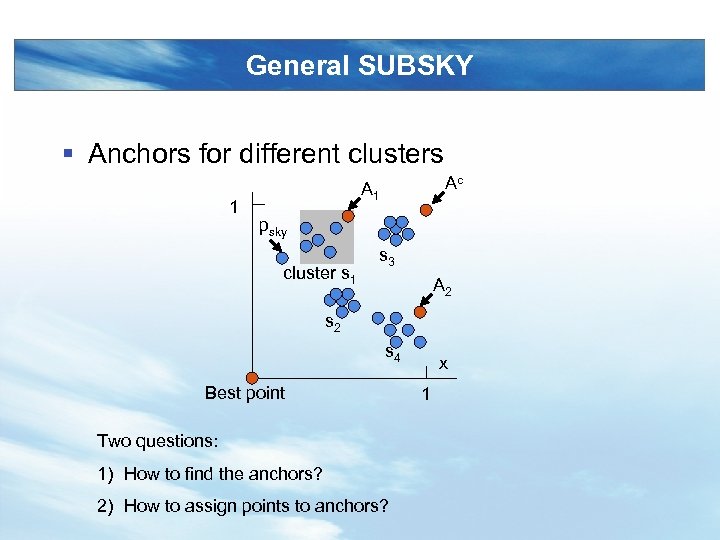
General SUBSKY § Anchors for different clusters 1 Ac A 1 psky cluster s 1 s 3 A 2 s 4 Best point Two questions: 1) How to find the anchors? 2) How to assign points to anchors? x 1

Finding the Anchors § First, let us see what a perfect anchor of a point p § If p is assigned to A, then p can be pruned by any skyline point dominating p Any point on this line is a perfect anchor ofc point p A A 3 1 A 2 Major perpendicular plane A 1 p Anti-dominant region of p Best point 1

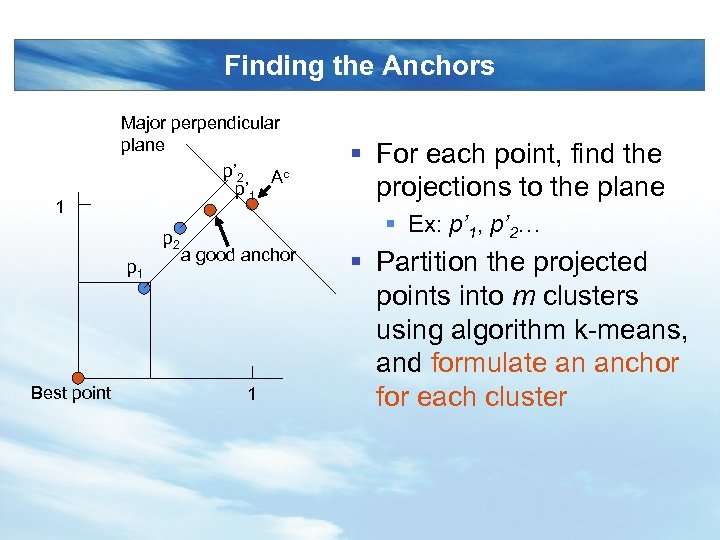
Finding the Anchors 1 Major perpendicular plane p’ 2 Ac p’ 1 p 2 p 1 Best point § For each point, find the projections to the plane § Ex: p’ 1, p’ 2… a good anchor 1 § Partition the projected points into m clusters using algorithm k-means, and formulate an anchor for each cluster

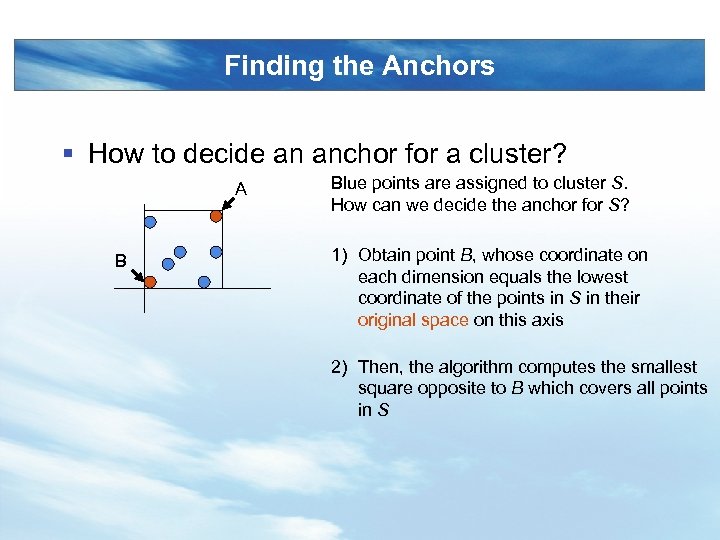
Finding the Anchors § How to decide an anchor for a cluster? A B Blue points are assigned to cluster S. How can we decide the anchor for S? 1) Obtain point B, whose coordinate on each dimension equals the lowest coordinate of the points in S in their original space on this axis 2) Then, the algorithm computes the smallest square opposite to B which covers all points in S

Assigning Points to Anchors § § A naïve way is to assign points to their closest anchor point in the major perpendicular plane (projected space) It is not directly quantifies the benefit of an assignment

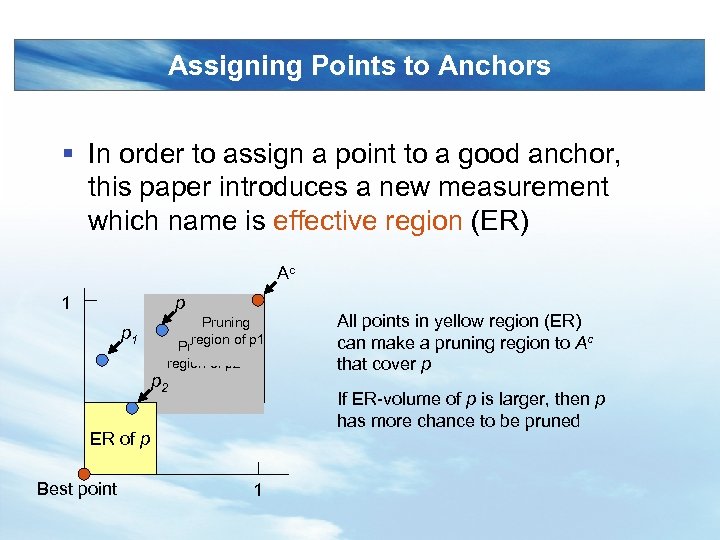
Assigning Points to Anchors § In order to assign a point to a good anchor, this paper introduces a new measurement which name is effective region (ER) Ac 1 p p 1 Pruning region of p 2 If ER-volume of p is larger, then p has more chance to be pruned ER of p Best point All points in yellow region (ER) can make a pruning region to Ac that cover p 1

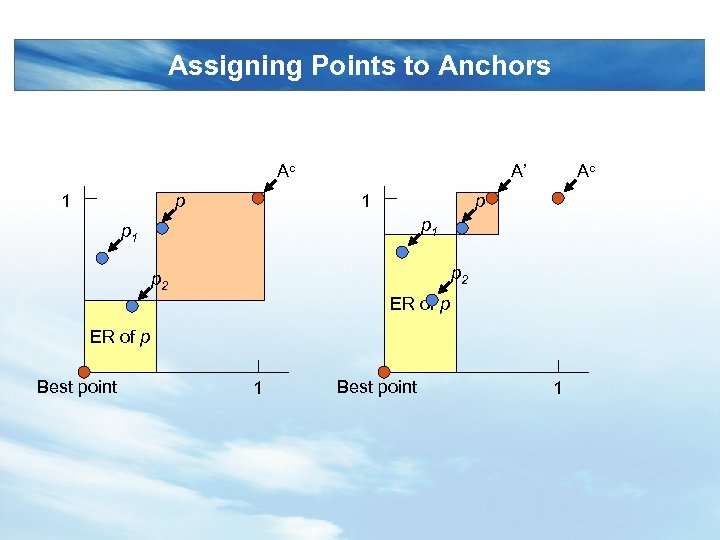
Assigning Points to Anchors Ac 1 p A’ 1 Ac p p 1 p 2 ER of p Best point 1

Assigning Points to Anchors § The pruning volume size of a point p to an anchor point Aj is ∏max(0, Aj[i]-L∞(p, Aj)), where i is from 1 to d § Therefore, assign a point p to Aj that produces the largest pruning volume size

Query example x y z f(pi) p 1 0. 2 0. 5 0. 8 p 2 0. 4 0. 9 0. 6 p 3 0. 5 0. 3 0. 1 0. 9 p 4 0. 9 0. 1 0. 6 0. 9 p 5 0. 6 0. 8 0. 7 0. 4 § We use the same example in previous slide § Assume that we have two anchors, one is Ac and the other A’ is found by K-means (m=1) § Ac=(1, 1, 1) and A’=(1, 1, 0. 8) § First, we calculate the ER volume of each data point with respect to Ac and A’ Ac A’ p 1 8 0 p 2 64 - p 3 1 9 p 4 1 - p 5 216 144 Unit 10 -3

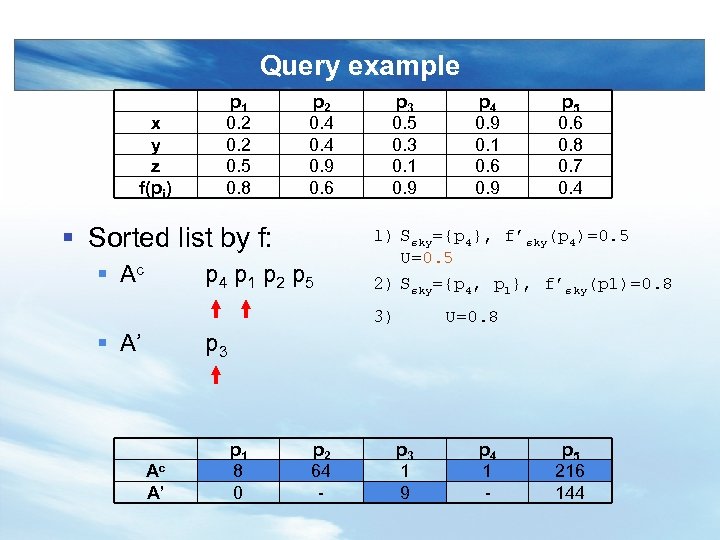
Query example x y z f(pi) p 1 0. 2 0. 5 0. 8 p 2 0. 4 0. 9 0. 6 § Sorted list by f: § Ac p 4 p 1 p 2 p 5 p 3 0. 5 0. 3 0. 1 0. 9 p 5 0. 6 0. 8 0. 7 0. 4 1) Ssky={p 4}, f’sky(p 4)=0. 5 U=0. 5 2) Ssky={p 4, p 1}, f’sky(p 1)=0. 8 3) § A’ p 4 0. 9 0. 1 0. 6 0. 9 U=0. 8 p 3 Ac A’ p 1 8 0 p 2 64 - p 3 1 9 p 4 1 - p 5 216 144

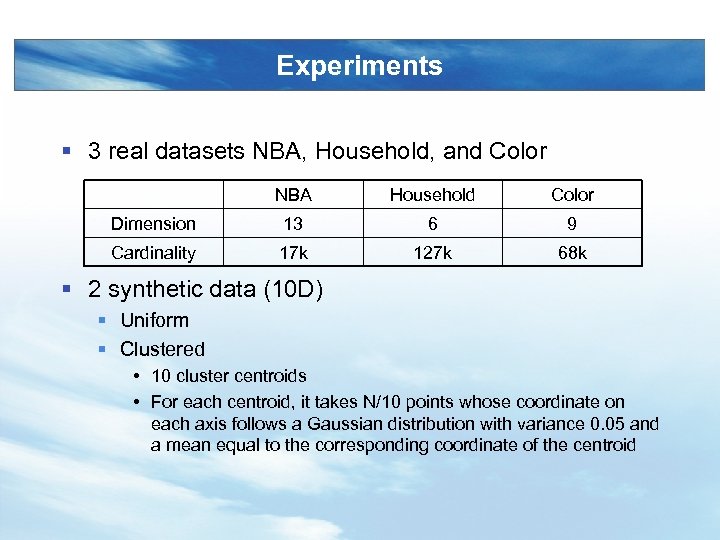
Experiments § 3 real datasets NBA, Household, and Color NBA Household Color Dimension 13 6 9 Cardinality 17 k 127 k 68 k § 2 synthetic data (10 D) § Uniform § Clustered • 10 cluster centroids • For each centroid, it takes N/10 points whose coordinate on each axis follows a Gaussian distribution with variance 0. 05 and a mean equal to the corresponding coordinate of the centroid

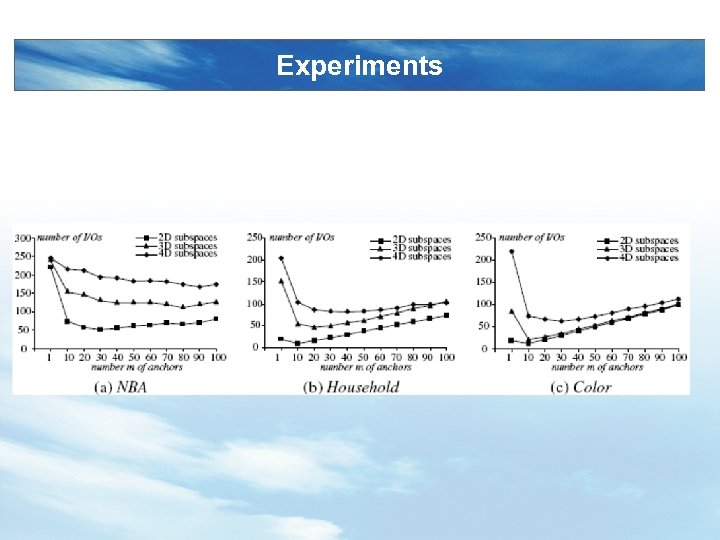
Experiments

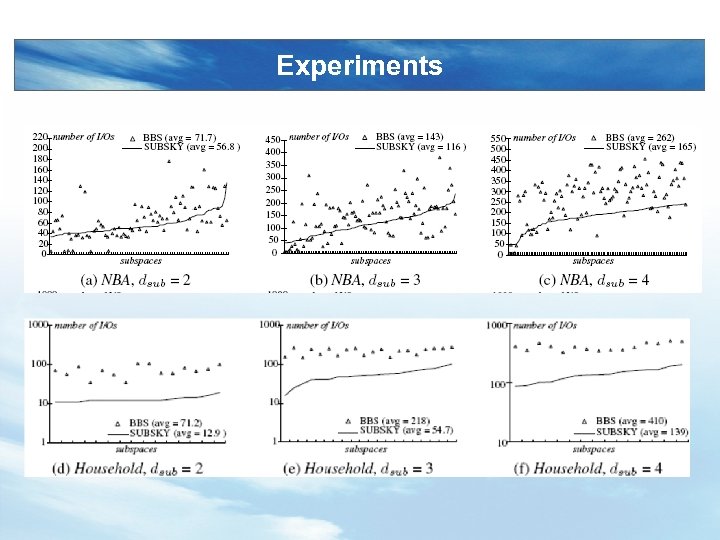
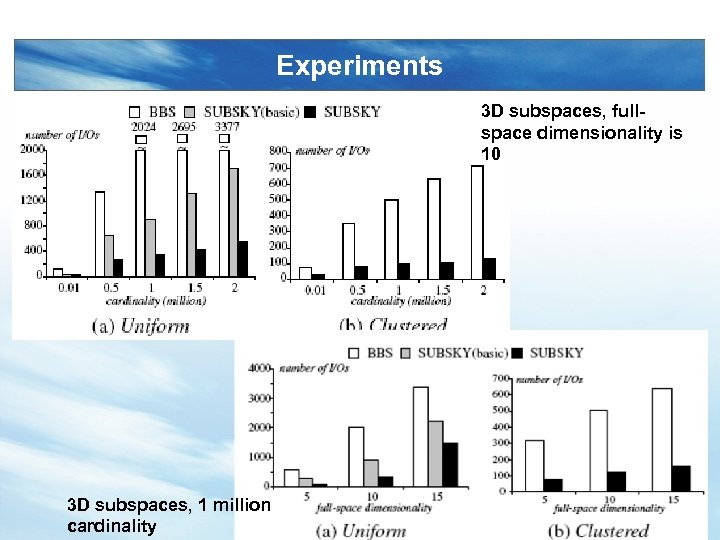
Experiments 3 D subspaces, fullspace dimensionality is 10 3 D subspaces, 1 million cardinality

Conclusion § The core of SUBSKY is a transformation that convert multi-dimensional data into 1 D values § Show better performance than a I/O optimized algorithm in the subspace skyline problem § Some continuous monitoring cases are good to investigate § How to adopt the set of anchor points if data update rapidly § The f values could be stored in other index structure to support fast update