Структурно параметрическое моделирование и идентификация модели технологического

“Структурно – параметрическое моделирование и идентификация модели технологического процесса формования помадных масс как объекта управления”

Нами были проведены экспериментальные исследования процесса формования помадных конфет, анализ результатов которых позволил получить структурно - параметрическую модель формования помадного жгута из матричного отверстия экструдера с переходом на транспортерную ленту. Схема размазного конвейера, который использовался для изучения поведения отформованных помадных масс представлена на данном рисунке

Одним из важнейших этапов производства помадных конфет, в значительной степени влияющим на качество получаемого готового кондитерского изделия, является процесс формования. Обзор и анализ большинства опубликованных работ по динамике процесса формования пищевых материалов рассматривают режимы течения этих материалов внутри формующих устройств: шнековых нагнетателей, предматричных пространств и разной конструкции каналов матриц. Но процесс формования готовых изделий может происходить и после выхода этих материалов из матричных отверстий в виде жгута. Цифровая видеосъемка показывает, что высота конфетного жгута h, а значит, и размеры корпуса конфеты, зависят от соотношения скорости выхода жгута из матричного отверстия vм и скорости движения транспортерной ленты vтл. При увеличении скорости выхода жгута за счет увеличения скорости нагнетания конфетной массы на проведенной нами видеозаписи видно, как увеличивается высота h конфетного жгута, лежащего на движущейся транспортерной ленте. Для построения параметрической модели были проведены исследования, в результате которых были определены входные и выходные параметры и случайные нерегулируемые воздействия, влияющие на процесс формования конфетных жгутов.

Свободный выход жгута из матричного отверстия. . Основной входной параметр в параметрической модели процесса формования – это скорость vм выхода жгута из матричного отверстия. Эту скорость можно изменять за счет изменения скорости нагнетания пищевой массы, которая зависит от скорости вращения шнека в шнековом нагнетателе или шестерен в шестеренном нагнетателе, как это сделано в экструдере линии производства помадных конфет. Вначале был рассмотрен процесс свободного выхода жгута из матричного отверстия. В общем случае, в зависимости от конструкции матричных отверстий, скорость выхода жгута пищевой массы может быть направлена под углом α к горизонту. Чаще всего при формовании изделий из пищевых материалов угол α = - 90° (отсадка конфетных масс, кондитерского теста и др. ). В экструдере линии производства помадных конфет, на которой проводились эксперименты, α = - 45°.

Описание входных выходных величин ограничениями Описание входных иивыходных величин с с ограничениями Входные величины Vm - скорость выхода массы из матричного отверстия ( от 9 до 15 мм/с); Выходные величины К(хк, 0) – координаты максимальной кривизны жгута после формования, т. е. изменение траектории жгута, характеризующая РСМ – реологические свойства помадных масс изменение его расстояния до точки касания ( от 4 х10 -2 Пас до 32 х10 -2 Пас); конфетным жгутом транспортерной ленты (может изменяться в диапазоне от 0 до 35 мм); Тф – температура помадной массы, поступающей на формование (от 32 С 0 до h - высота конфетного жгута на выходе (может 0). 42 С изменяться от 0, 8 до 1, 2 мм); Vтл - скорость транспортерной ленты при проведении эксперимента была постоянной - 22, 68 мм/с, (может меняться от 20 до 24, 5 мм/с); S(х1, х2) – изменение удельной площади жгута, выходящего из матричного отверстия формующей машины (диапазон изменения удельной площади в рабочем режиме от -0, 5 до 0, 36 , т. е. размах составляет 0, 86 ); М(х, у) - расстояние от момента выхода до точки касания конфетного жгута транспортерной ленты, в рабочем режиме может изменяться в диапазоне от -1, 0 до 2, 4 мм, т. е. на 3, 4 мм.

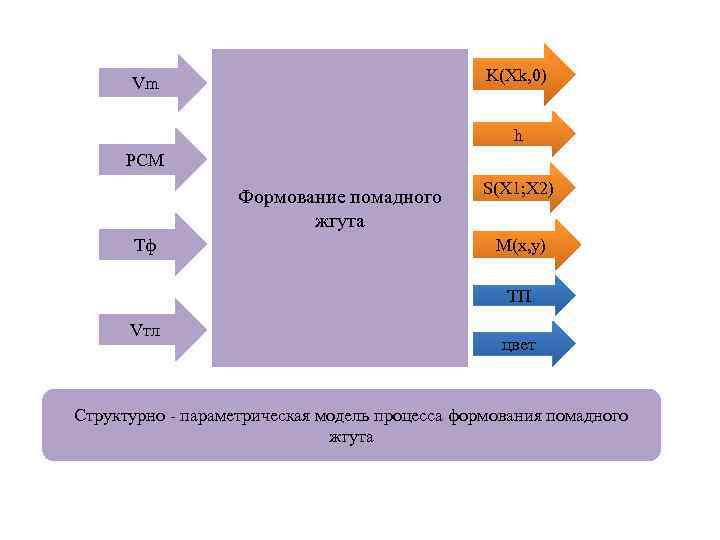K(Xk, 0) Vm h PCM Формование помадного жгута Tф S(X 1; X 2) M(x, y) ТП Vтл цвет Структурно - параметрическая модель процесса формования помадного жгута

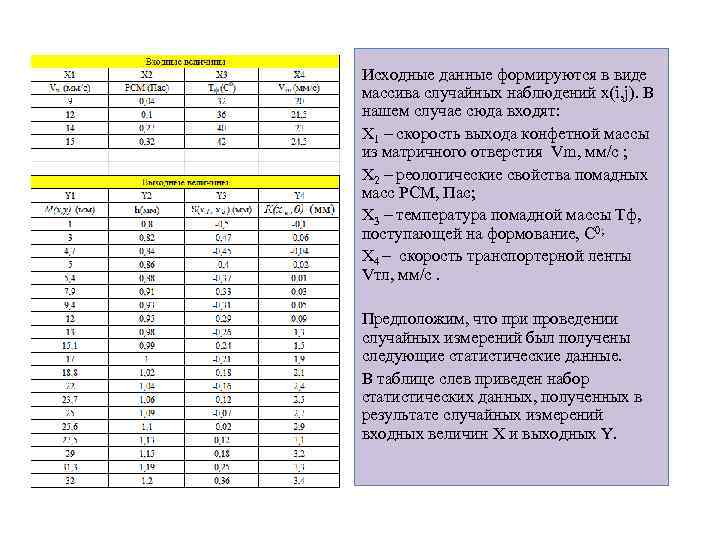Исходные данные формируются в виде массива случайных наблюдений x(i, j). В нашем случае сюда входят: X 1 – скорость выхода конфетной массы из матричного отверстия Vm, мм/с ; X 2 – реологические свойства помадных масс РСМ, Пас; Х 3 – температура помадной массы Тф, поступающей на формование, С 0; X 4 – скорость транспортерной ленты Vтл, мм/с. Предположим, что при проведении случайных измерений был получены следующие статистические данные. В таблице слев приведен набор статистических данных, полученных в результате случайных измерений входных величин X и выходных Y.

Составим уравнения Протодьяконова для X 1, X 2, X 3, X 4 через программу Method и обобщенные критерии оптимальности для W 1 и W 2 через программу Eureka = Полученные уравнения Протодьяконова • • Y 1=(28. 94 -6. 15*X 1+0. 405*X 1^2)*(19. 30118. 29*X 2+82. 21*X 2^2)*(18. 569+0. 145*X 30. 002*X 3^2)*(22. 051. 099*X 4+0. 043*X 4^2)/34, 803 Y 2=(107. 12 -22. 72*X 1+1. 14*X 1^2)*(7. 5941. 205*X 2 -0. 181*X 2^2)*(6. 206+0. 132*X 30. 002*X 3^2)*(22. 362. 17*X 4+0. 066*X 4^2)/34, 803 Y 3=(-63. 34+26. 51*X 12. 31*X 1^2)*(6. 903+0. 256*X 20. 063*X 2^2)*(11. 772. 24*X 3+0. 202*X 3^2)*(4. 633+0. 282*X 4+0. 0 27*X 4^2)/34, 803 Y 4=(-59. 907+25. 102*X 12. 14*X 1^2)*(7. 942+0. 329*X 20. 063*X 2^2)*(13. 422. 33*X 3+0. 207*X 3^2)*(6. 063+0. 2609*X 4+0. 027*X 4^2)/34, 803 Уравнения для решения обобщенных критериев оптимальности • W 1= • W 2= Ограничения для w 1 Ограничения для w 2

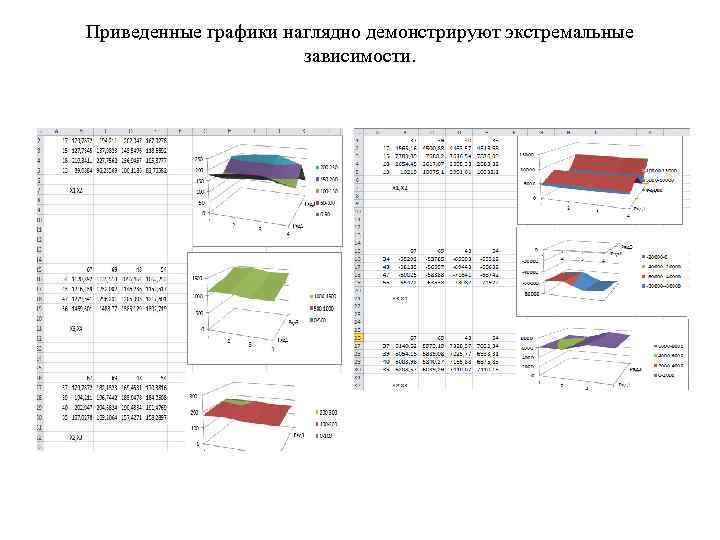Приведенные графики наглядно демонстрируют экстремальные зависимости.

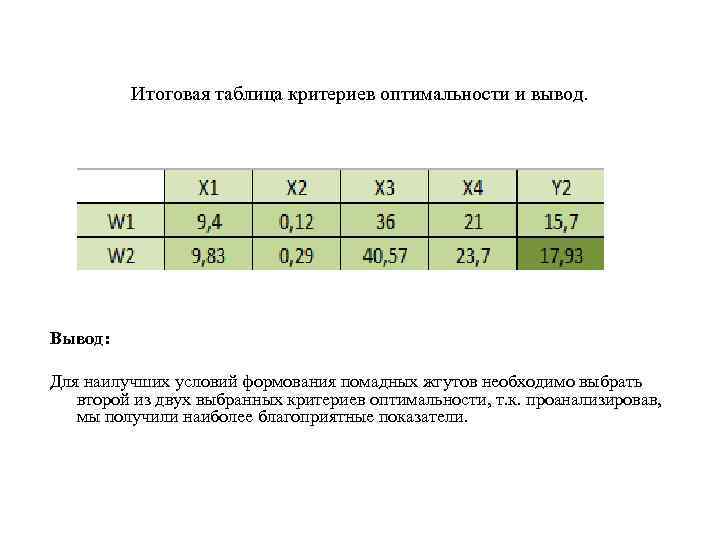Итоговая таблица критериев оптимальности и вывод. Вывод: Для наилучших условий формования помадных жгутов необходимо выбрать второй из двух выбранных критериев оптимальности, т. к. проанализировав, мы получили наиболее благоприятные показатели.