Strukturni_schemy.ppt
- Количество слайдов: 48
 Структурні схеми систем автоматичного керування 1 Умовні позначення в структурних схемах систем автоматичного керування 2 З’єднання ланок в структурних схемах 3 Складання структурних схем систем автоматичного керування 4 Перетворення структурних схем 5 Передаточні функції замкнутих систем автоматичного керування
Структурні схеми систем автоматичного керування 1 Умовні позначення в структурних схемах систем автоматичного керування 2 З’єднання ланок в структурних схемах 3 Складання структурних схем систем автоматичного керування 4 Перетворення структурних схем 5 Передаточні функції замкнутих систем автоматичного керування
 Умовні позначення в структурних схемах систем автоматичного керування § Структурна схема – це умовне зображення системи автоматичного керування у вигляді сукупності динамічних ланок з вказівкою зв'язків між ними
Умовні позначення в структурних схемах систем автоматичного керування § Структурна схема – це умовне зображення системи автоматичного керування у вигляді сукупності динамічних ланок з вказівкою зв'язків між ними
 Умовні позначення в структурних схемах систем автоматичного керування § Структурна схема складається за відомими рівняннями динаміки САК § Рівняння динаміки САК можуть бути отримані за відомою структурною схемою
Умовні позначення в структурних схемах систем автоматичного керування § Структурна схема складається за відомими рівняннями динаміки САК § Рівняння динаміки САК можуть бути отримані за відомою структурною схемою
 Умовні позначення в структурних схемах систем автоматичного керування § Ланка структурної схеми – прямокутник, у якому відображуються у вигляді передаточної функції рівняння динаміки § Допускається застосовувати умовні позначення передаточної функції, а її записати окремо
Умовні позначення в структурних схемах систем автоматичного керування § Ланка структурної схеми – прямокутник, у якому відображуються у вигляді передаточної функції рівняння динаміки § Допускається застосовувати умовні позначення передаточної функції, а її записати окремо
 Умовні позначення в структурних схемах систем автоматичного керування X 1(p) X 3(p)=X 1(p)+X 2(p) X 1(p) X 3(p)=X 1(p)-X 2(p) § Ланка, яка забезпечує алгебраїчне підсумовування вхідних величин зображається у вигляді кола, поділеного на чотири сектори. Така ланка називається суматором § Якщо вхідні величини подаються з від’ємним знаком, то відповідний сектор затушовується. Така ланка називається елементом порівняння
Умовні позначення в структурних схемах систем автоматичного керування X 1(p) X 3(p)=X 1(p)+X 2(p) X 1(p) X 3(p)=X 1(p)-X 2(p) § Ланка, яка забезпечує алгебраїчне підсумовування вхідних величин зображається у вигляді кола, поділеного на чотири сектори. Така ланка називається суматором § Якщо вхідні величини подаються з від’ємним знаком, то відповідний сектор затушовується. Така ланка називається елементом порівняння
 Умовні позначення в структурних схемах систем автоматичного керування § Розділення X 1(p) сигналів зображається у вигляді крапки у місці з'єднання ліній. § Це місце називається вузол
Умовні позначення в структурних схемах систем автоматичного керування § Розділення X 1(p) сигналів зображається у вигляді крапки у місці з'єднання ліній. § Це місце називається вузол
 З’єднання ланок в структурних схемах § Послідовне з'єднання – вихідний сигнал попередньої ланки подається на вхід наступної W 1(p) W 2(p)
З’єднання ланок в структурних схемах § Послідовне з'єднання – вихідний сигнал попередньої ланки подається на вхід наступної W 1(p) W 2(p)
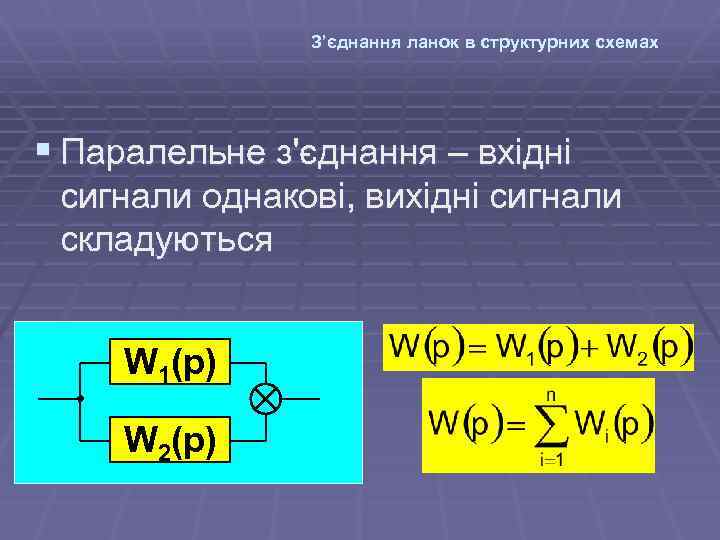 З’єднання ланок в структурних схемах § Паралельне з'єднання – вхідні сигнали однакові, вихідні сигнали складуються W 1(p) W 2(p)
З’єднання ланок в структурних схемах § Паралельне з'єднання – вхідні сигнали однакові, вихідні сигнали складуються W 1(p) W 2(p)
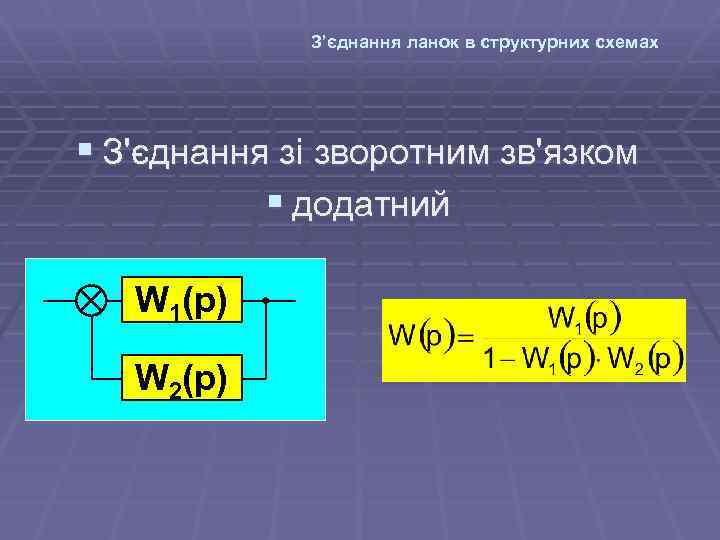 З’єднання ланок в структурних схемах § З'єднання зі зворотним зв'язком § додатний W 1(p) W 2(p)
З’єднання ланок в структурних схемах § З'єднання зі зворотним зв'язком § додатний W 1(p) W 2(p)
 З’єднання ланок в структурних схемах § З'єднання зі зворотним зв'язком § від'ємний W 1(p) W 2(p)
З’єднання ланок в структурних схемах § З'єднання зі зворотним зв'язком § від'ємний W 1(p) W 2(p)
 З’єднання ланок в структурних схемах § З'єднання зі зворотним зв'язком при W 2(p)=1 § додатний W 1(p)
З’єднання ланок в структурних схемах § З'єднання зі зворотним зв'язком при W 2(p)=1 § додатний W 1(p)
 З’єднання ланок в структурних схемах § З'єднання зі зворотним зв'язком при W 2(p)=1 § від'ємний W 1(p)
З’єднання ланок в структурних схемах § З'єднання зі зворотним зв'язком при W 2(p)=1 § від'ємний W 1(p)
 Складання структурних схем систем автоматичного керування § Рівняння динаміки системи автоматичного керування (1. 1) (1. 2) (1. 3)
Складання структурних схем систем автоматичного керування § Рівняння динаміки системи автоматичного керування (1. 1) (1. 2) (1. 3)
 Складання структурних схем систем автоматичного керування (1. 4) (1. 5)
Складання структурних схем систем автоматичного керування (1. 4) (1. 5)
 Складання структурних схем систем автоматичного керування (1. 6) (1. 7)
Складання структурних схем систем автоматичного керування (1. 6) (1. 7)
 Складання структурних схем систем автоматичного керування § Рівняння динаміки в операторному виді (2. 1) (2. 2) (2. 3)
Складання структурних схем систем автоматичного керування § Рівняння динаміки в операторному виді (2. 1) (2. 2) (2. 3)
 Складання структурних схем систем автоматичного керування (2. 4) (2. 5) (2. 6) (2. 7)
Складання структурних схем систем автоматичного керування (2. 4) (2. 5) (2. 6) (2. 7)
 Складання структурних схем систем автоматичного керування § Знаходження параметрів системи автоматичного керування (3. 1) (3. 2) (3. 3)
Складання структурних схем систем автоматичного керування § Знаходження параметрів системи автоматичного керування (3. 1) (3. 2) (3. 3)
 Складання структурних схем систем автоматичного керування (3. 4) (3. 5)
Складання структурних схем систем автоматичного керування (3. 4) (3. 5)
 Складання структурних схем систем автоматичного керування (3. 6) (3. 7)
Складання структурних схем систем автоматичного керування (3. 6) (3. 7)
 Складання структурних схем систем автоматичного керування § Введемо позначення
Складання структурних схем систем автоматичного керування § Введемо позначення
 Складання структурних схем систем автоматичного керування § Отримаємо
Складання структурних схем систем автоматичного керування § Отримаємо
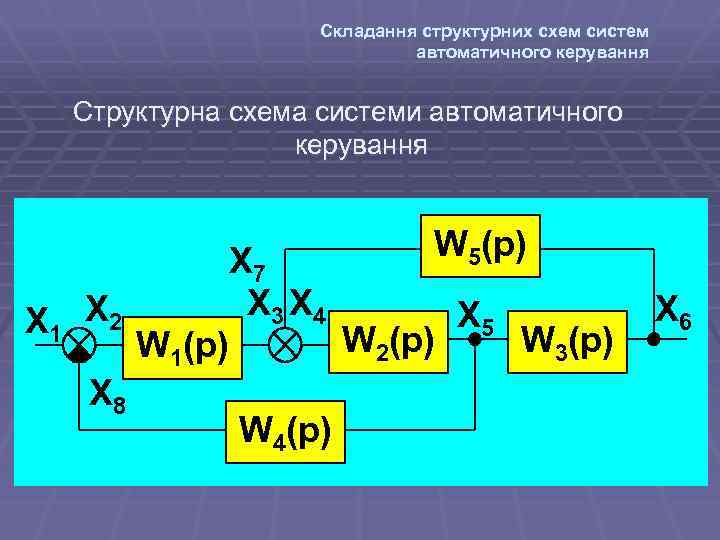 Складання структурних схем систем автоматичного керування Структурна схема системи автоматичного керування X 1 X 2 X 8 W 1(p) X 7 X 3 X 4 W 4(p) W 5(p) W 2(p) X 5 W 3(p) X 6
Складання структурних схем систем автоматичного керування Структурна схема системи автоматичного керування X 1 X 2 X 8 W 1(p) X 7 X 3 X 4 W 4(p) W 5(p) W 2(p) X 5 W 3(p) X 6
 Перетворення структурних схем Після перетворення структурної схеми сигнал на виході системи повинен бути таким же, як і до перетворення
Перетворення структурних схем Після перетворення структурної схеми сигнал на виході системи повинен бути таким же, як і до перетворення
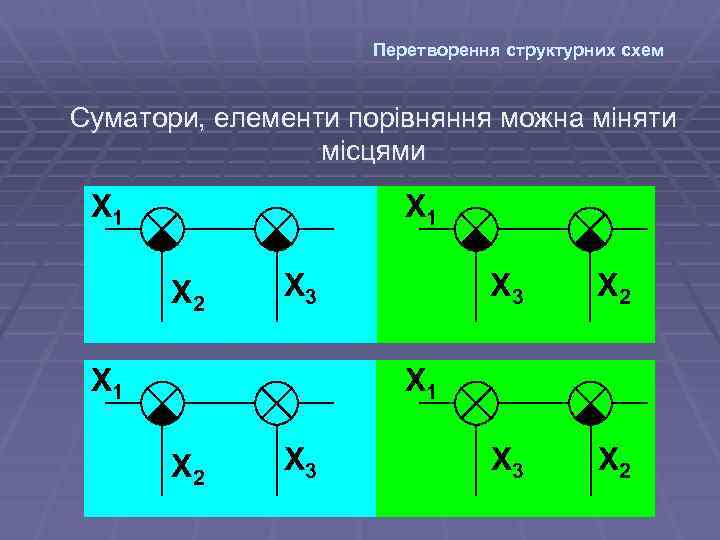 Перетворення структурних схем Суматори, елементи порівняння можна міняти місцями X 1 X 2 X 3 X 1 X 3 X 2 X 1 X 2 X 3
Перетворення структурних схем Суматори, елементи порівняння можна міняти місцями X 1 X 2 X 3 X 1 X 3 X 2 X 1 X 2 X 3
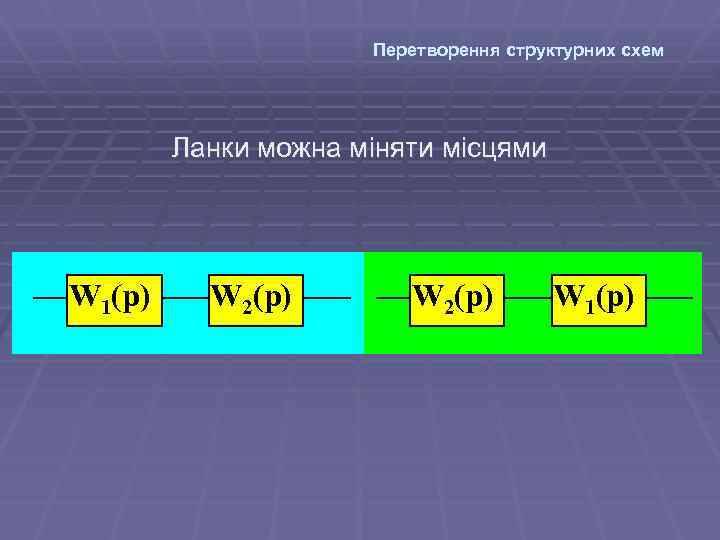 Перетворення структурних схем Ланки можна міняти місцями W 1(p) W 2(p) W 1(p)
Перетворення структурних схем Ланки можна міняти місцями W 1(p) W 2(p) W 1(p)
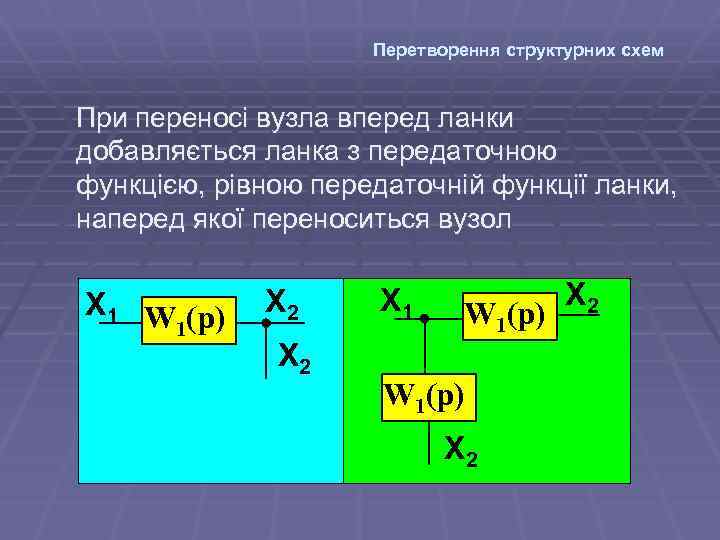 Перетворення структурних схем При переносі вузла вперед ланки добавляється ланка з передаточною функцією, рівною передаточній функції ланки, наперед якої переноситься вузол Х 1 W (p) 1 Х 2 Х 1 W 1(p) Х 2
Перетворення структурних схем При переносі вузла вперед ланки добавляється ланка з передаточною функцією, рівною передаточній функції ланки, наперед якої переноситься вузол Х 1 W (p) 1 Х 2 Х 1 W 1(p) Х 2
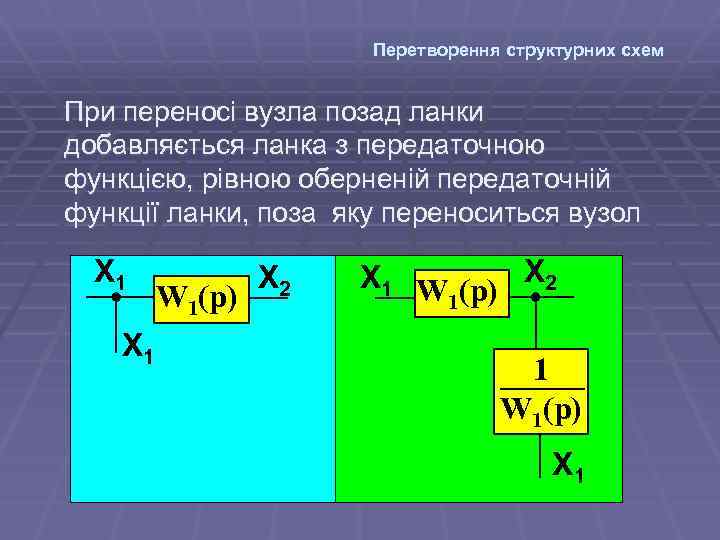 Перетворення структурних схем При переносі вузла позад ланки добавляється ланка з передаточною функцією, рівною оберненій передаточній функції ланки, поза яку переноситься вузол Х 1 W 1(p) Х 2 Х 1 W (p) Х 2 1 1 W 1(p) Х 1
Перетворення структурних схем При переносі вузла позад ланки добавляється ланка з передаточною функцією, рівною оберненій передаточній функції ланки, поза яку переноситься вузол Х 1 W 1(p) Х 2 Х 1 W (p) Х 2 1 1 W 1(p) Х 1
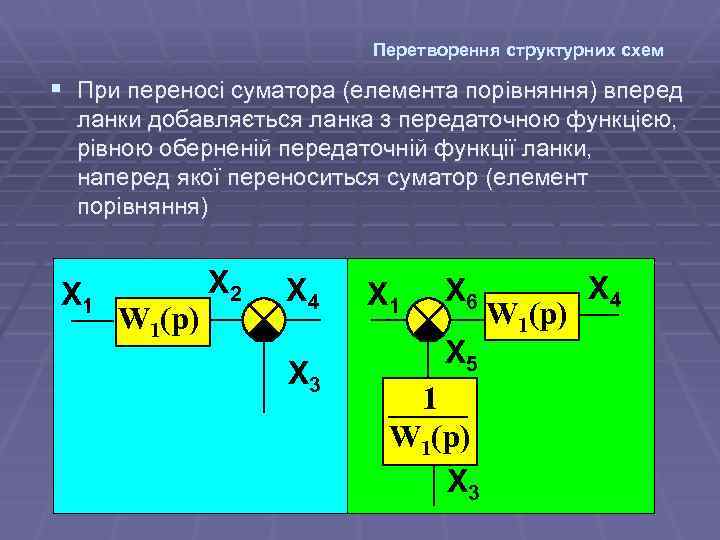 Перетворення структурних схем § При переносі суматора (елемента порівняння) вперед ланки добавляється ланка з передаточною функцією, рівною оберненій передаточній функції ланки, наперед якої переноситься суматор (елемент порівняння) Х 1 W 1(p) Х 2 X 4 Х 3 Х 1 X 6 X 5 1 W 1(p) Х 3 W 1(p) Х 4
Перетворення структурних схем § При переносі суматора (елемента порівняння) вперед ланки добавляється ланка з передаточною функцією, рівною оберненій передаточній функції ланки, наперед якої переноситься суматор (елемент порівняння) Х 1 W 1(p) Х 2 X 4 Х 3 Х 1 X 6 X 5 1 W 1(p) Х 3 W 1(p) Х 4
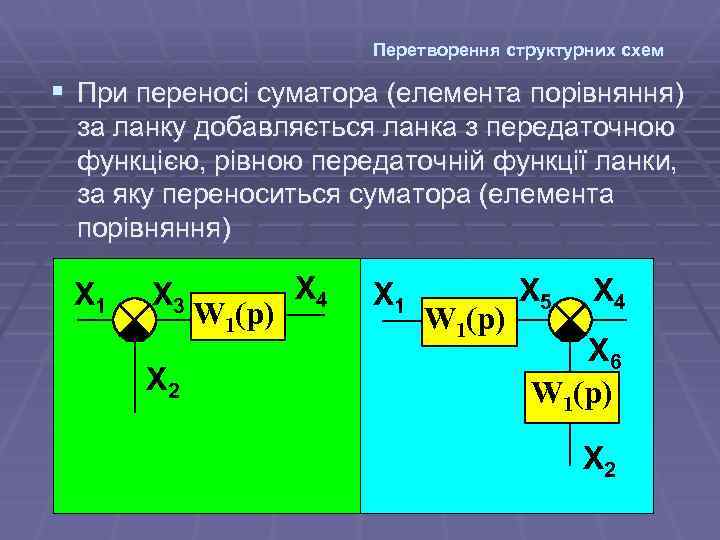 Перетворення структурних схем § При переносі суматора (елемента порівняння) за ланку добавляється ланка з передаточною функцією, рівною передаточній функції ланки, за яку переноситься суматора (елемента порівняння) Х 1 Х 3 Х 2 W 1(p) Х 4 Х 1 W 1(p) X 5 X 4 Х 6 W 1(p) Х 2
Перетворення структурних схем § При переносі суматора (елемента порівняння) за ланку добавляється ланка з передаточною функцією, рівною передаточній функції ланки, за яку переноситься суматора (елемента порівняння) Х 1 Х 3 Х 2 W 1(p) Х 4 Х 1 W 1(p) X 5 X 4 Х 6 W 1(p) Х 2
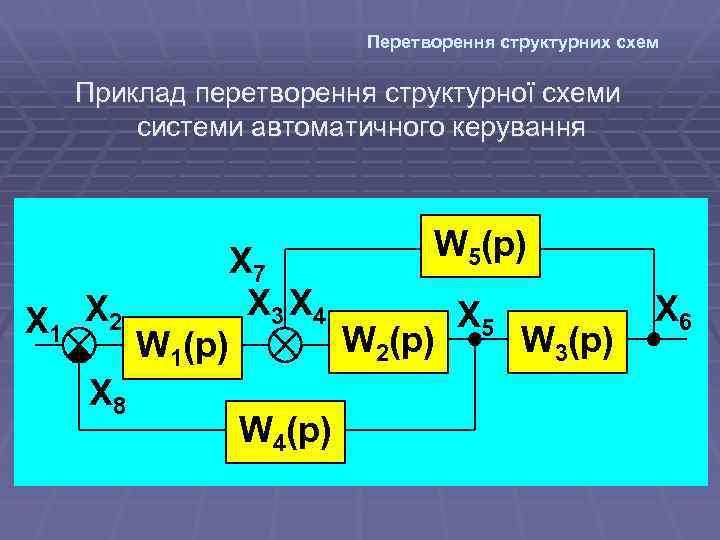 Перетворення структурних схем Приклад перетворення структурної схеми системи автоматичного керування X 1 X 2 X 8 W 1(p) X 7 X 3 X 4 W 4(p) W 5(p) W 2(p) X 5 W 3(p) X 6
Перетворення структурних схем Приклад перетворення структурної схеми системи автоматичного керування X 1 X 2 X 8 W 1(p) X 7 X 3 X 4 W 4(p) W 5(p) W 2(p) X 5 W 3(p) X 6
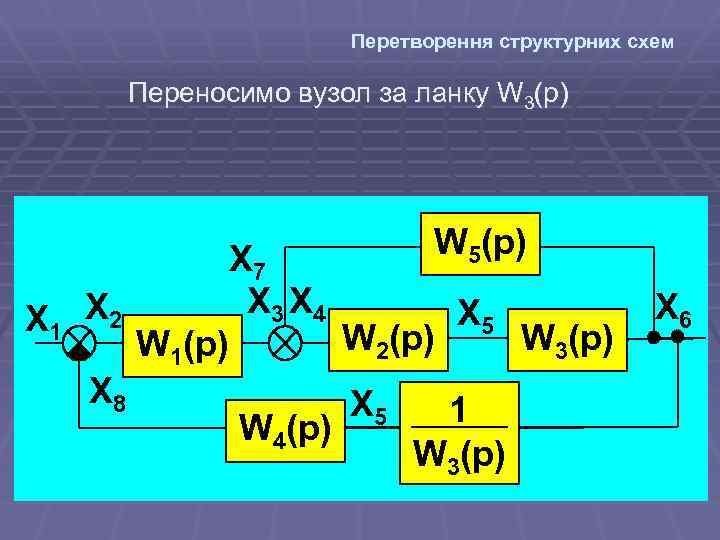 Перетворення структурних схем Переносимо вузол за ланку W 3(p) X 1 X 2 X 8 W 1(p) X 7 X 3 X 4 W 4(p) W 5(p) W 2(p) X 5 1 W 3(p) X 6
Перетворення структурних схем Переносимо вузол за ланку W 3(p) X 1 X 2 X 8 W 1(p) X 7 X 3 X 4 W 4(p) W 5(p) W 2(p) X 5 1 W 3(p) X 6
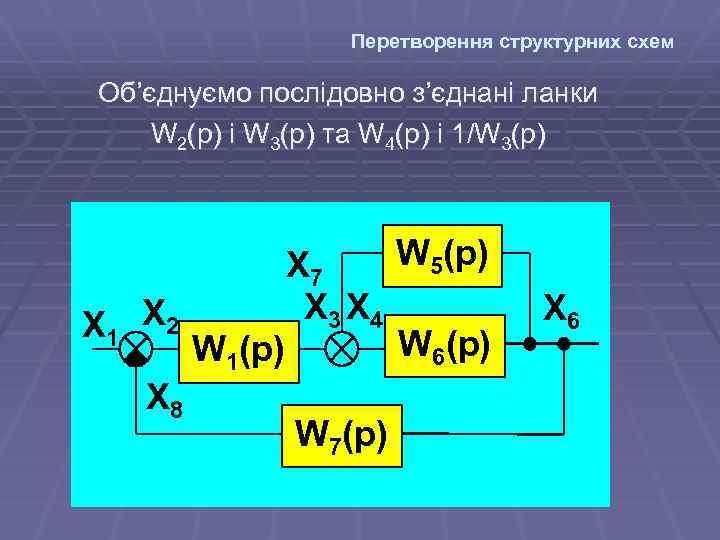 Перетворення структурних схем Об’єднуємо послідовно з’єднані ланки W 2(р) і W 3(р) та W 4(р) і 1/W 3(р) X 1 W 5(p) X 7 X 3 X 4 X 2 W 6(p) W 1(p) X 8 W 7(p) X 6
Перетворення структурних схем Об’єднуємо послідовно з’єднані ланки W 2(р) і W 3(р) та W 4(р) і 1/W 3(р) X 1 W 5(p) X 7 X 3 X 4 X 2 W 6(p) W 1(p) X 8 W 7(p) X 6
 Перетворення структурних схем Передаточні функції нових ланок
Перетворення структурних схем Передаточні функції нових ланок
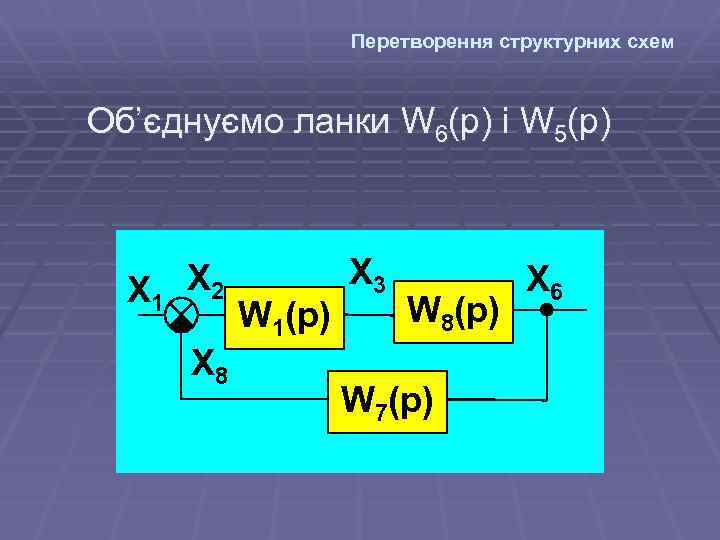 Перетворення структурних схем Об’єднуємо ланки W 6(р) і W 5(р) X 1 X 2 X 8 W 1(p) X 3 W 8(p) W 7(p) X 6
Перетворення структурних схем Об’єднуємо ланки W 6(р) і W 5(р) X 1 X 2 X 8 W 1(p) X 3 W 8(p) W 7(p) X 6
 Перетворення структурних схем Передаточна функція нової ланки
Перетворення структурних схем Передаточна функція нової ланки
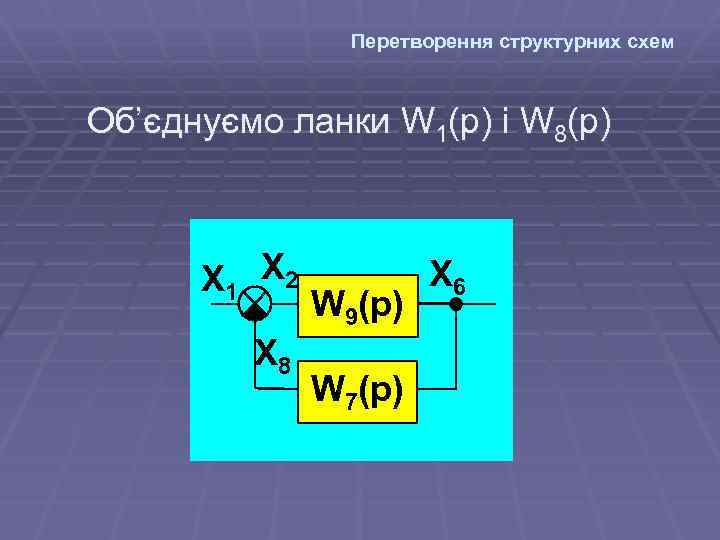 Перетворення структурних схем Об’єднуємо ланки W 1(р) і W 8(р) X 1 X 2 X 8 W 9(p) W 7(p) X 6
Перетворення структурних схем Об’єднуємо ланки W 1(р) і W 8(р) X 1 X 2 X 8 W 9(p) W 7(p) X 6
 Перетворення структурних схем Передаточна функція нової ланки
Перетворення структурних схем Передаточна функція нової ланки
 Перетворення структурних схем Нарешті отримуємо систему, яка складається з одної ланки X 1 W 10(p) X 6 з передаточною функцією
Перетворення структурних схем Нарешті отримуємо систему, яка складається з одної ланки X 1 W 10(p) X 6 з передаточною функцією
 Передаточні функції замкнутих систем автоматичного керування § В теорії автоматичного керування розглядаються замкнуті системи з одиничним зворотним зв’язком g(t) ε(t) Wp(p) x(t)
Передаточні функції замкнутих систем автоматичного керування § В теорії автоматичного керування розглядаються замкнуті системи з одиничним зворотним зв’язком g(t) ε(t) Wp(p) x(t)
 Передаточні функції замкнутих систем автоматичного керування § Якщо розімкнути зворотний зв’язок, то отримаємо розімкнутий ланцюг системи автоматичного керування g(t) ε(t) Wp(p) x(t)
Передаточні функції замкнутих систем автоматичного керування § Якщо розімкнути зворотний зв’язок, то отримаємо розімкнутий ланцюг системи автоматичного керування g(t) ε(t) Wp(p) x(t)
 Передаточні функції замкнутих систем автоматичного керування § Передаточною функцією розімкнутого ланцюга системи автоматичного керування називається відношення зображень по Лапласу вихідного сигналу до похибки при нульових початкових умовах і відсутності збурень
Передаточні функції замкнутих систем автоматичного керування § Передаточною функцією розімкнутого ланцюга системи автоматичного керування називається відношення зображень по Лапласу вихідного сигналу до похибки при нульових початкових умовах і відсутності збурень
 Передаточні функції замкнутих систем автоматичного керування Передаточна функція розімкнутої системи має велике значення в теорії автоматичного керування. Вона використовується при аналізі і синтезі САК
Передаточні функції замкнутих систем автоматичного керування Передаточна функція розімкнутої системи має велике значення в теорії автоматичного керування. Вона використовується при аналізі і синтезі САК
 Передаточні функції замкнутих систем автоматичного керування Передаточні функції замкнутої системи автоматичного керування § головна передаточна функція § передаточна функція за помилкою § передаточна функція за збуренням § передаточна функція за помилкою від збурення
Передаточні функції замкнутих систем автоматичного керування Передаточні функції замкнутої системи автоматичного керування § головна передаточна функція § передаточна функція за помилкою § передаточна функція за збуренням § передаточна функція за помилкою від збурення
 Передаточні функції замкнутих систем автоматичного керування Головна передаточна функція
Передаточні функції замкнутих систем автоматичного керування Головна передаточна функція
 Передаточні функції замкнутих систем автоматичного керування Передаточна функція за помилкою
Передаточні функції замкнутих систем автоматичного керування Передаточна функція за помилкою
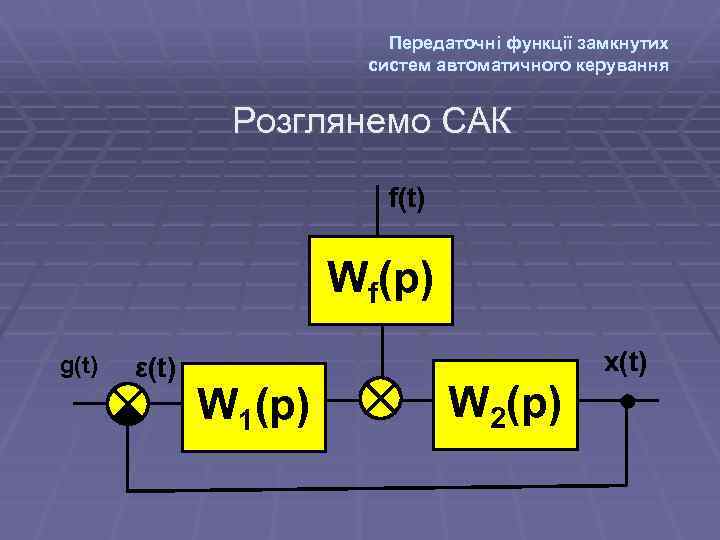 Передаточні функції замкнутих систем автоматичного керування Розглянемо САК f(t) Wf(p) g(t) ε(t) x(t) W 1(p) W 2(p)
Передаточні функції замкнутих систем автоматичного керування Розглянемо САК f(t) Wf(p) g(t) ε(t) x(t) W 1(p) W 2(p)
 Передаточні функції замкнутих систем автоматичного керування Передаточна функція за збуренням
Передаточні функції замкнутих систем автоматичного керування Передаточна функція за збуренням


