Lekcii po metrologii.ppt
- Количество слайдов: 131

Структура лекций по метрологии • Общие понятия • Измерения. Виды. Погрешности • Направления метрологического обеспечения • Современные тенденции развития метрологии

Общие понятия «Измеряй всё доступное измерению, и делай доступным всё недоступное ему. » Галилео Галилей
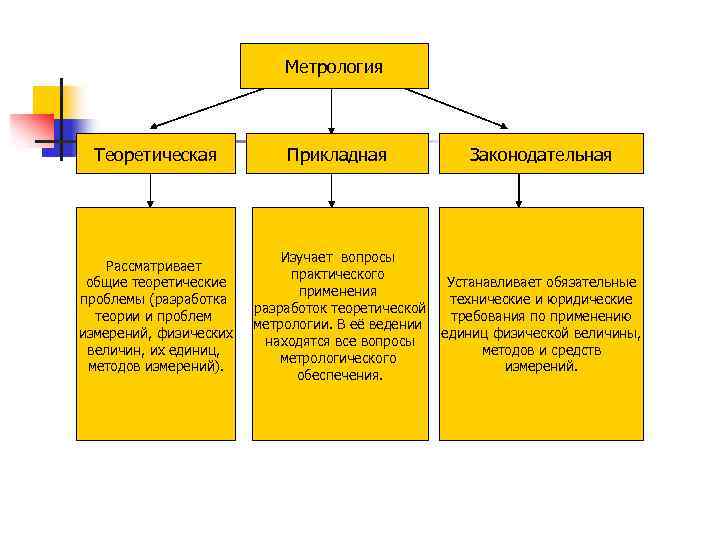
Метрология Теоретическая Прикладная Рассматривает общие теоретические проблемы (разработка теории и проблем измерений, физических величин, их единиц, методов измерений). Изучает вопросы практического применения разработок теоретической метрологии. В её ведении находятся все вопросы метрологического обеспечения. Законодательная Устанавливает обязательные технические и юридические требования по применению единиц физической величины, методов и средств измерений.

n n „Метрология является важнейшей стороной сложного процесса усовершенствования технологии и качества продукции. В то же время именно метрология необходима для обнаружения областей несогласованности в научных исследованиях и потому обнаруживает те области, в которых можно ждать принципиальных сдвигов в науке. . . Только страна, имеющая передовое приборостроение и метрологию, может быть передовой в науке ". n Академик А. П. Александров

Цели и задачи метрологии n n n Создание общей теории измерений; Образование единиц физических величин и систем единиц; Разработка и стандартизация методов и средств измерений, методов определения точности измерений, основ обеспечения единства измерений и единообразия средств измерений (так называемая «законодательная метрология» ); Создание эталонов и образцовых средств измерений, поверка мер и средств измерений. Приоритетной подзадачей данного направления является выработка системы эталонов на основе физических констант. Также метрология изучает развитие системы мер, денежных единиц и счёта в исторической перспективе.
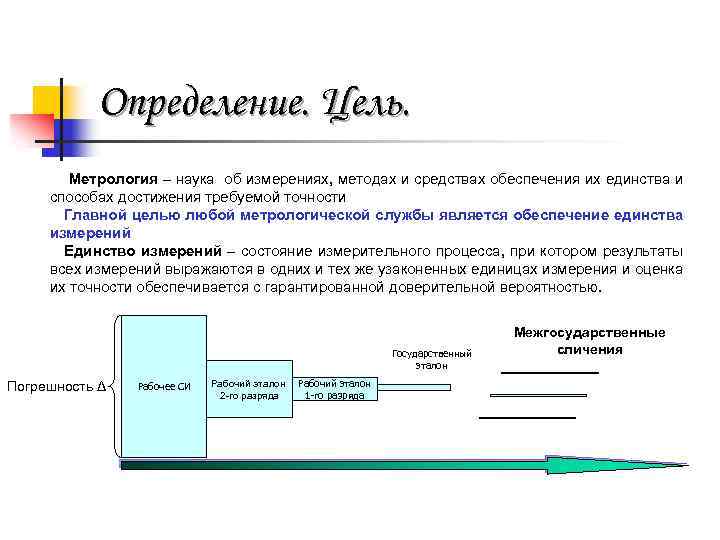
Определение. Цель. Метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности Главной целью любой метрологической службы является обеспечение единства измерений Единство измерений – состояние измерительного процесса, при котором результаты всех измерений выражаются в одних и тех же узаконенных единицах измерения и оценка их точности обеспечивается с гарантированной доверительной вероятностью. Государственный эталон Погрешность Δ Рабочее СИ Рабочий эталон 2 -го разряда Рабочий эталон 1 -го разряда Межгосударственные сличения
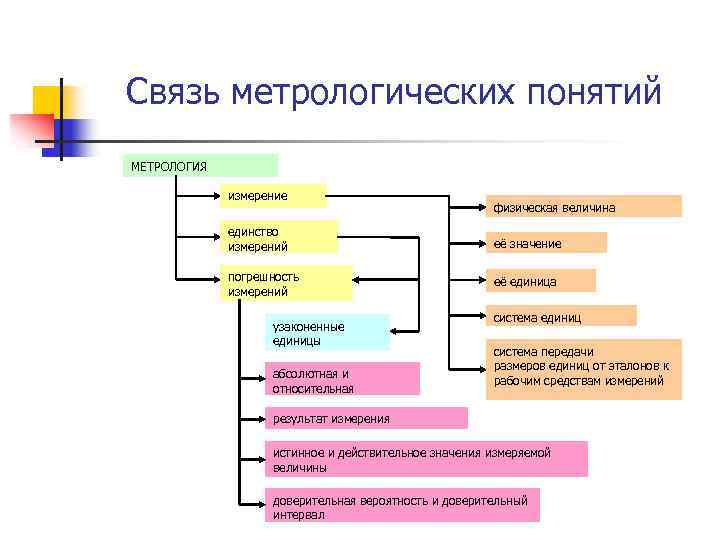
Связь метрологических понятий МЕТРОЛОГИЯ измерение физическая величина единство измерений её значение погрешность измерений её единица узаконенные единицы абсолютная и относительная система единиц система передачи размеров единиц от эталонов к рабочим средствам измерений результат измерения истинное и действительное значения измеряемой величины доверительная вероятность и доверительный интервал

Виды эталонов и их свойства n n n n Вид эталона: Первичный эталон - эталон, обеспечивающий воспроизведение единицы с наивысшей в стране (по сравнению с другими эталонами той же единицы) точностью. Вторичный (или специальный) эталон воспроизводит единицу в особых условиях и заменяет при этих условия первичный эталон. Он создается и утверждается в тех случаях, когда это необходимо для обеспечения наименьшего износа государственного эталона. Вторичные эталоны по своему назначению делятся на эталоны-копии, эталоны сравнения, эталоны-свидетели и рабочие эталоны. Государственный или национальный - это первичный или специальный эталон, официально утвержденный в качестве исходного для страны. Государственные эталоны создаются, хранятся и применяются центральными метрологическими научными институтами страны. Точность воспроизведения единицы должна соответствовать уровню лучших мировых достижений и удовлетворять потребностям науки и техники. Эталон-копия предназначен для передачи размеров единиц рабочим эталонам. Он не всегда является физической копией государственного эталона. Эталон-свидетель предназначен для проверки сохранности государственного эталона и для замены его в случае порчи или утраты. Эталон сравнения применяют для сличения эталонов, которые по тем или иным причинам не могут быть непосредственно сличаемы друг с другом. Рабочий эталон воспроизводит единицу от вторичных эталонов и служит для передачи размера эталону более низкого разряда.

« Торговые все дела вести без пакости, ни умаливати, ни умноживати, а на всякий год увещевати» Устав новгородского князя Всеволода «О церковных судах и о людях и о мерилах торговли» , 1136 год
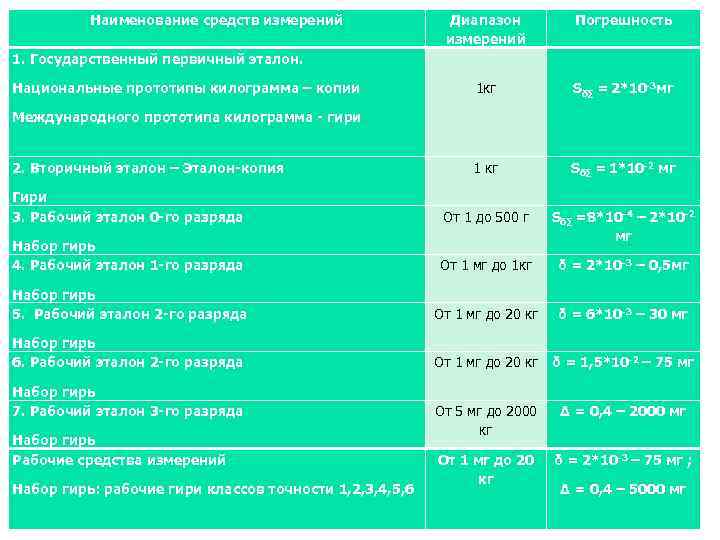
Наименование средств измерений Диапазон измерений Погрешность 1 кг Sδ∑ = 2*10 -3 мг 1 кг Sδ∑ = 1*10 -2 мг Гири 3. Рабочий эталон 0 -го разряда От 1 до 500 г Набор гирь 4. Рабочий эталон 1 -го разряда Sδ∑ =8*10 -4 – 2*10 -2 мг От 1 мг до 1 кг δ = 2*10 -3 – 0, 5 мг Набор гирь 5. Рабочий эталон 2 -го разряда От 1 мг до 20 кг δ = 6*10 -3 – 30 мг Набор гирь 6. Рабочий эталон 2 -го разряда От 1 мг до 20 кг δ = 1, 5*10 -2 – 75 мг От 5 мг до 2000 кг Δ = 0, 4 – 2000 мг От 1 мг до 20 кг δ = 2*10 -3 – 75 мг ; 1. Государственный первичный эталон. Национальные прототипы килограмма – копии Международного прототипа килограмма - гири 2. Вторичный эталон – Эталон-копия Набор гирь 7. Рабочий эталон 3 -го разряда Набор гирь Рабочие средства измерений Набор гирь: рабочие гири классов точности 1, 2, 3, 4, 5, 6 Δ = 0, 4 – 5000 мг
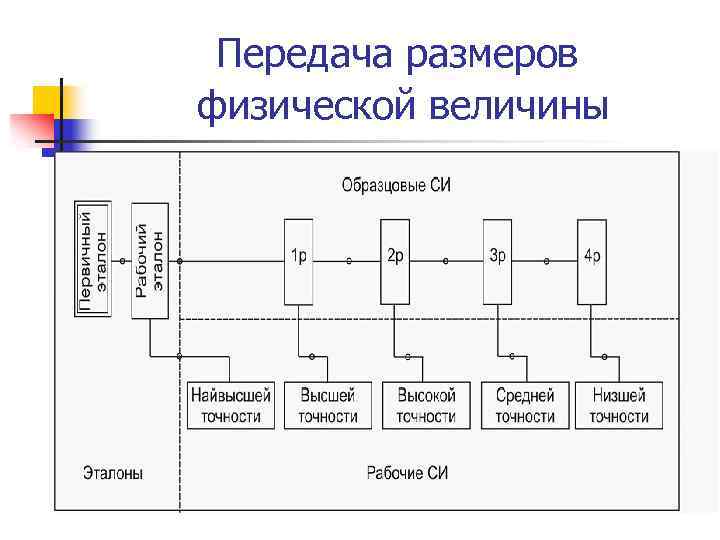
Передача размеров физической величины
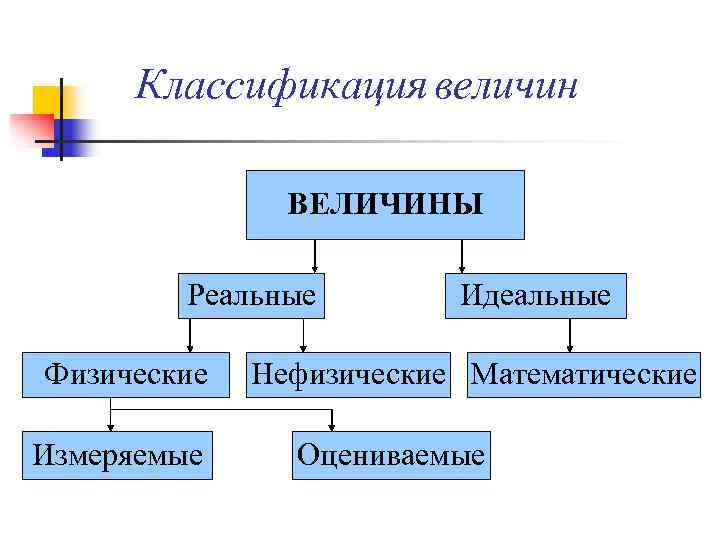
Классификация величин ВЕЛИЧИНЫ Реальные Физические Измеряемые Идеальные Нефизические Математические Оцениваемые
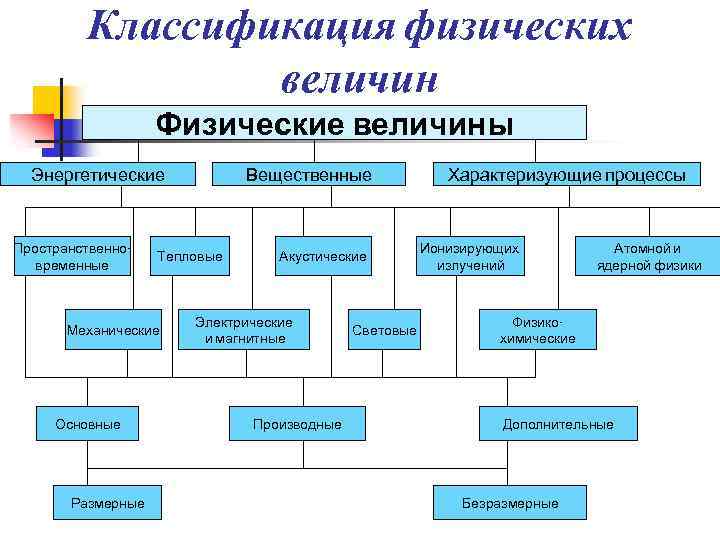
Классификация физических величин Физические величины Энергетические Пространственновременные Тепловые Механические Основные Размерные Вещественные Акустические Электрические и магнитные Производные Световые Характеризующие процессы Ионизирующих излучений Атомной и ядерной физики Физикохимические Дополнительные Безразмерные

Мерить дюйм на свой аршин патриотично, но утомительно. n В. Шендерович

Международная система СИ Единица измерения Обозначение русское название международное название русское международное Длина метр metre (meter) м m Масса килограмм kilogram кг kg Время секунда second с s Сила электрического тока ампер ampere А A Термодинамическая температура кельвин kelvin К K Сила света кандела candela кд cd Количество вещества моль mole моль mol Величина Метрическая конвенция — международный договор, служащий для обеспечения единства измерений в разных странах. Договор был подписан в 1875 г. в Париже 17 -ю странами, в том числе Россией. В настоящее время к конвенции присоединилось 51 государство, в том числе все промышленно-развитые страны.
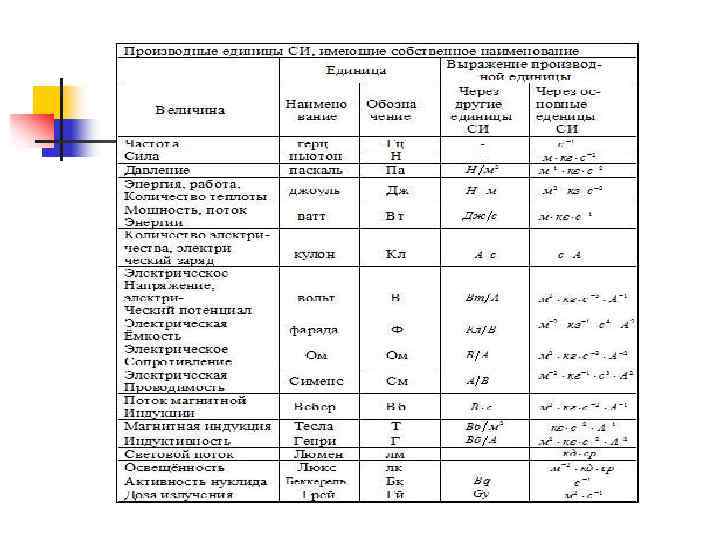
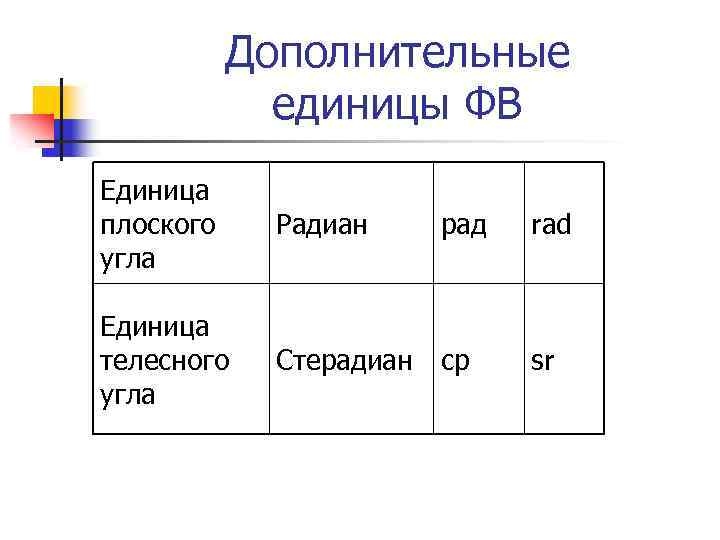
Дополнительные единицы ФВ Единица плоского угла Радиан рад rad Единица телесного угла Стерадиан ср sr
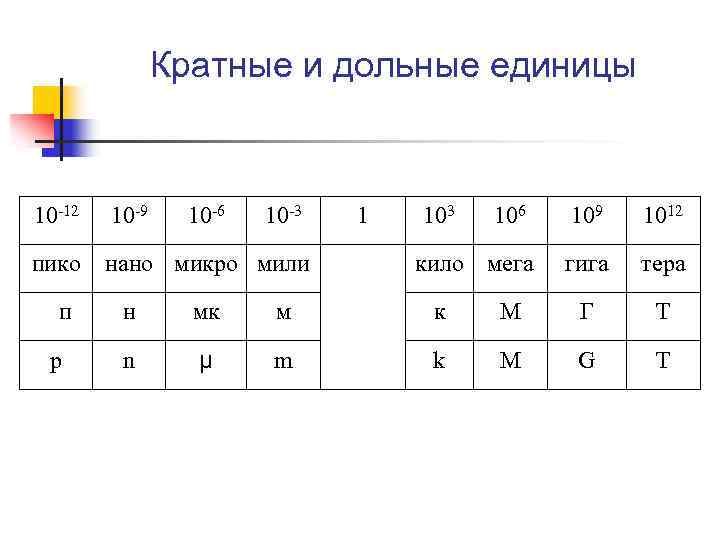
Кратные и дольные единицы 10 -12 10 -9 пико нано микро мили п p 10 -6 10 -3 1 103 106 109 1012 кило мега гига тера н мк м к М Г Т n µ m k M G T

Кратные и дольные единицы метра Кратные Дольные величина название обозначение величина название 101 м декаметр дам 102 м гектометр 103 м обозначение dam 10− 1 м дециметр дм dm гм hm 10− 2 м сантиметр см cm километр км km 10− 3 м миллиметр мм mm 106 м мегаметр Мм Mm 10− 6 м микрометр мкм µm 109 м гигаметр Гм Gm 10− 9 м нанометр нм nm 1012 м тераметр Тм Tm 10− 12 м пикометр пм pm 1015 м петаметр Пм Pm 10− 15 м фемтометр фм fm 1018 м эксаметр Эм Em 10− 18 м аттометр ам am 1021 м зеттаметр Зм Zm 10− 21 м зептометр зм zm 1024 м йоттаметр Им Ym 10− 24 м йоктометр им ym Десятичные кратные и дольные единицы образуются с помощью стандартных приставок СИ. Существуют также внесистемные единицы измерения: микрон, равный 1 мкм, и ангстрем (Å), равный 0, 1 нм, но их применение не рекомендуется.

Русские «метрологические» пословицы, переведенные по системе СИ, будут звучать так: n n n «от горшка 8, 8 сантиметра» ; « 1, 26 метра во лбу» ; «проглотил 71, 1 сантиметра» .
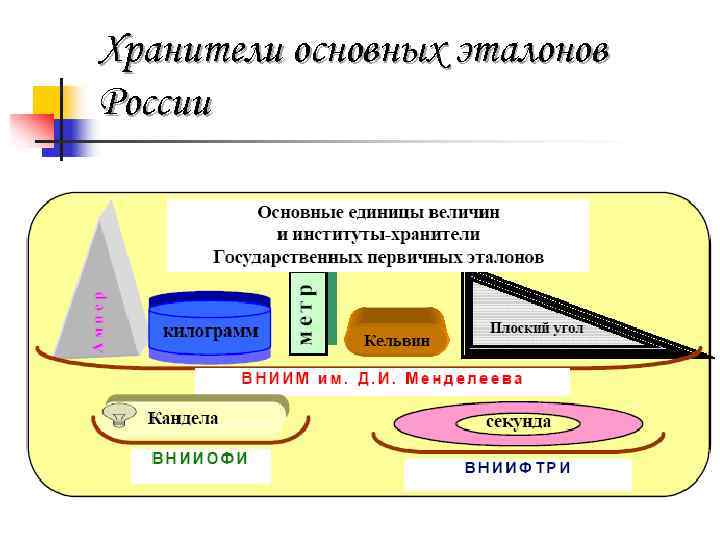
Хранители основных эталонов России
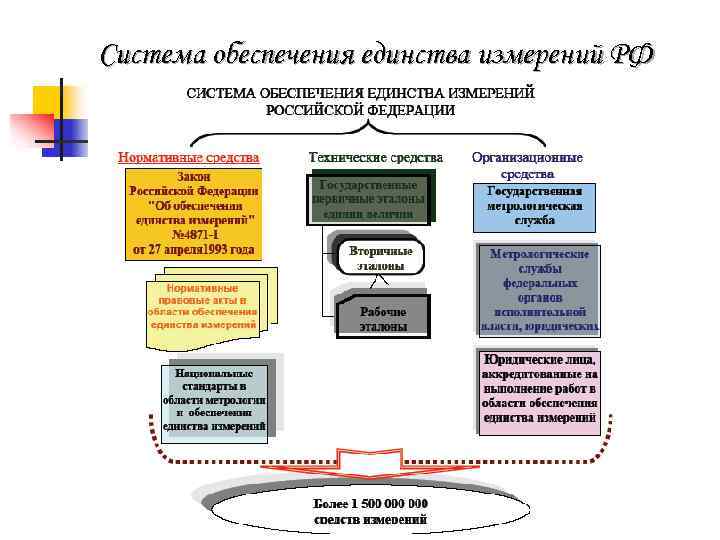
Система обеспечения единства измерений РФ
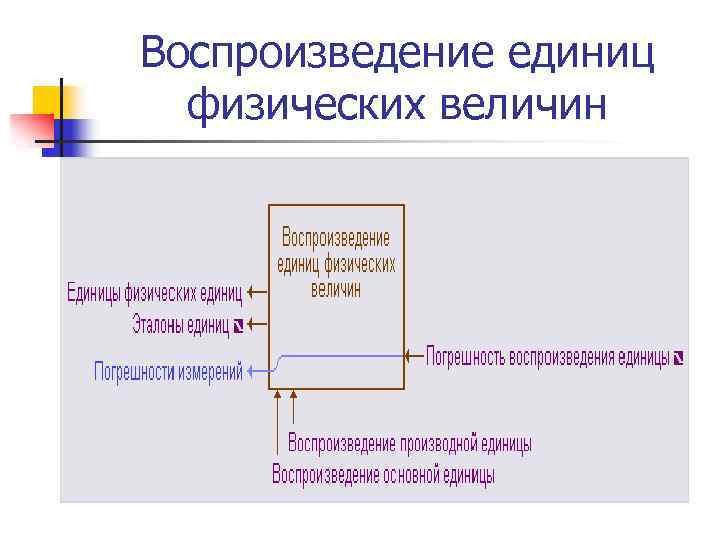
Воспроизведение единиц физических величин

Принципы обеспечения единства измерений Существуют принципы обеспечения единства измерений, к основным из которых относятся: • воспроизведение физических величин (ФВ) с помощью государственных эталонов; • применение только узаконенных единиц физических величин – международная система СИ; • применение узаконенных средств измерений, которые прошли государственные испытания и которым переданы размеры единиц ФВ от государственных эталонов – внесение в Госреестр СИ; • обязательный периодический контроль через установленные промежутки времени характеристик применяемых средств измерений – периодическая поверка, калибровка СИ; • гарантия обеспечения необходимой точности измерений при использовании поверенных средств измерений и аттестованных методик выполнения измерений – аттестация СИ; • использование результатов измерений только при условии оценки их погрешности с заданной вероятностью – расчет погрешности измерений; • систематический контроль за соблюдением метрологических правил и норм, государственный надзор и ведомственный контроль за средствами измерений.

Физическая величина – случайная функция n «Всякая неверная цифра – ошибка, а всякая лишняя цифра – половина ошибки» Академик А. Н. Крылов
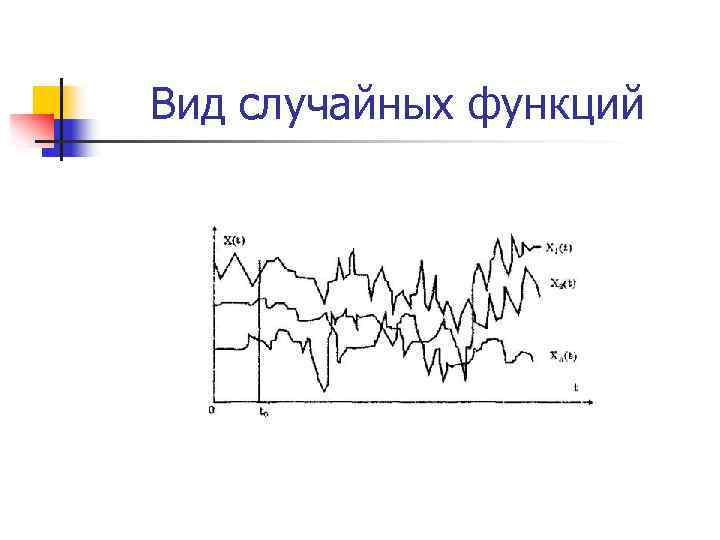
Вид случайных функций
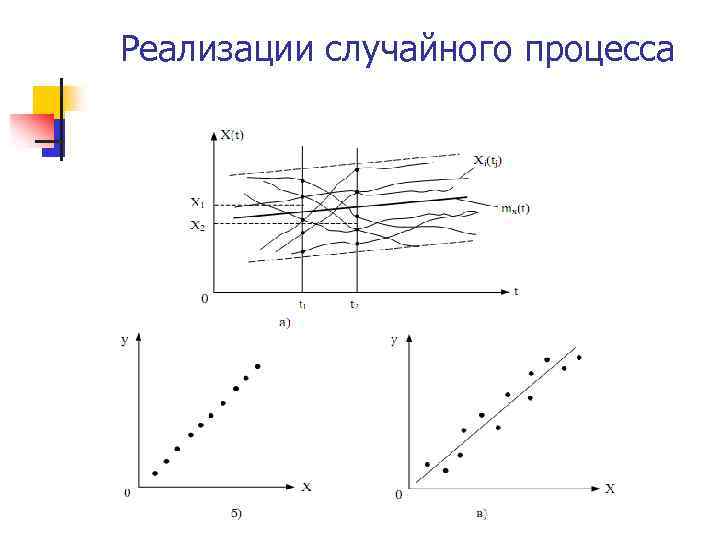
Реализации случайного процесса

Понятие измерения n «Каждая вещь известна лишь в той степени, в какой ее можно измерить» . Уильям Томсон, лорд Кельвин

Аксиомы метрологии 1. Любое измерение есть сравнение. 2. Любое измерение без априорной информации невозможно. 3. Результат любого измерения без округления значения является случайной величиной.
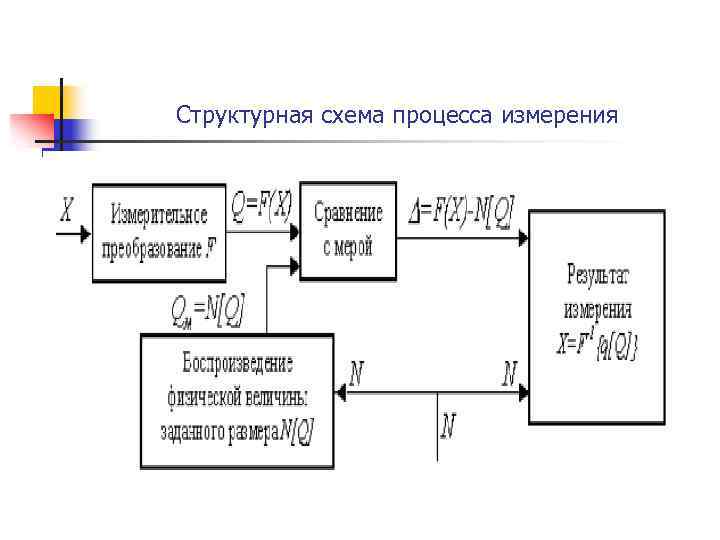
Структурная схема процесса измерения
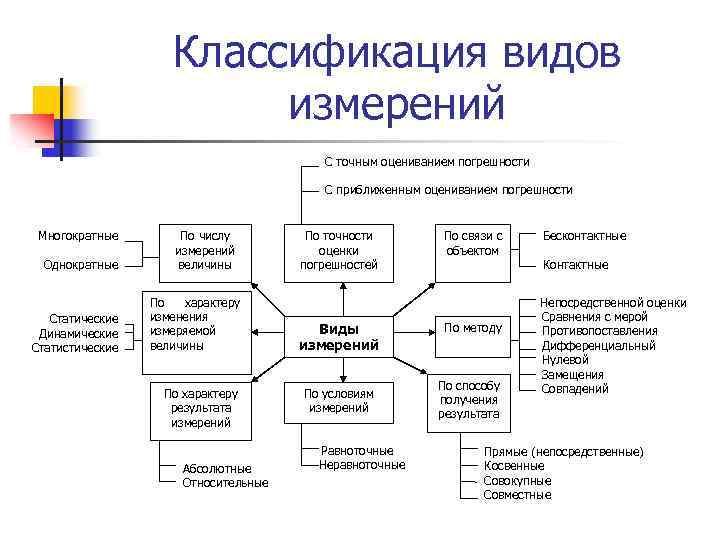
Классификация видов измерений С точным оцениванием погрешности С приближенным оцениванием погрешности Многократные Однократные Статические Динамические Статистические По числу измерений величины По характеру изменения измеряемой величины По характеру результата измерений По точности оценки погрешностей Бесконтактные Контактные Непосредственной оценки Виды измерений По условиям измерений Равноточные Абсолютные Относительные По связи с объектом Неравноточные По методу По способу получения результата Сравнения с мерой Противопоставления Дифференциальный Нулевой Замещения Совпадений Прямые (непосредственные) Косвенные Совокупные Совместные
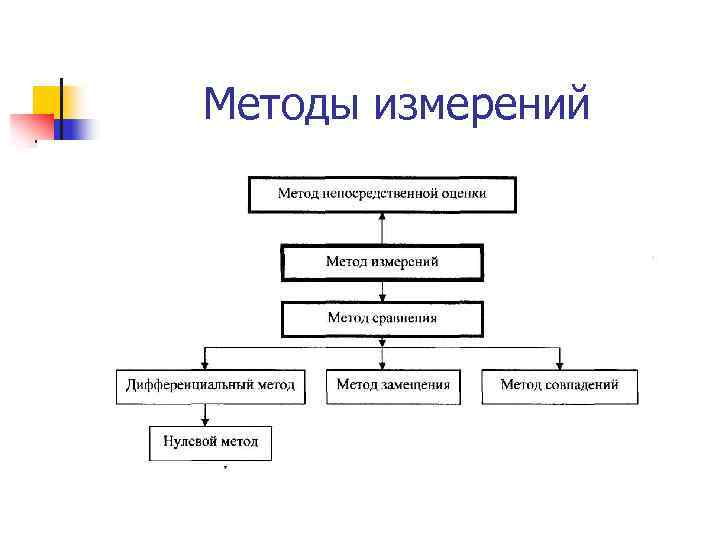
Методы измерений

n Любая наука начинается с измерений, а метрология – наука об измерениях, следовательно, метрология – это наука всех наук.
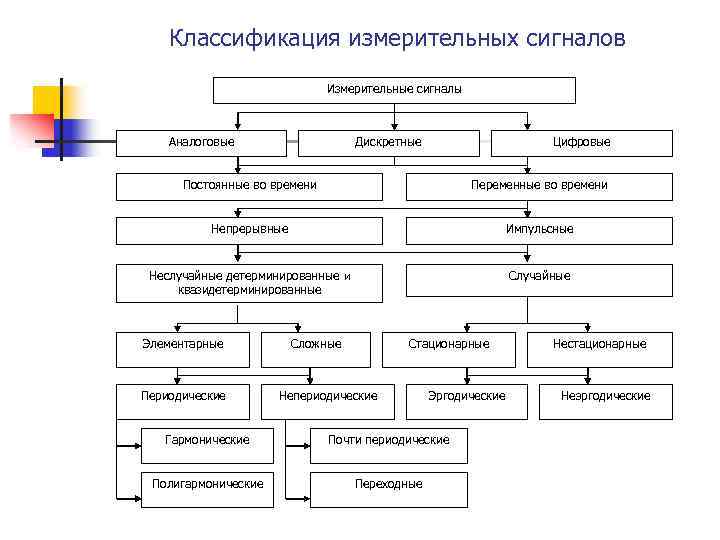
Классификация измерительных сигналов Измерительные сигналы Аналоговые Дискретные Цифровые Постоянные во времени Переменные во времени Непрерывные Импульсные Неслучайные детерминированные и квазидетерминированные Случайные Элементарные Периодические Сложные Стационарные Непериодические Эргодические Гармонические Почти периодические Полигармонические Переходные Нестационарные Неэргодические

Средства измерений физических величин n

Одинаковые приборы, проверенные одинаковым способом, будут в эксплуатации вести себя совершенно по-разному. n

Средство измерений (СИ) - техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени.

Тип средства измерений - совокупность средств измерений одного и того же назначения, основанных на одном и том же принципе действия, имеющих одинаковую конструкцию и изготовленных по одной и той же технической документации. Примечание - Средства измерений одного типа могут иметь различные модификации (например, отличаться по диапазону измерений)

Надежность оборудования обратно пропорциональна числу и положению лиц, за ним наблюдающих. n

Вид средства измерений - совокупность средств измерений, предназначенных для измерений данной физической величины. Примечание - Вид средств измерений может включать несколько их типов. Пример - Амперметры и вольтметры являются видами средств измерений, соответственно, силы электрического тока и напряжения
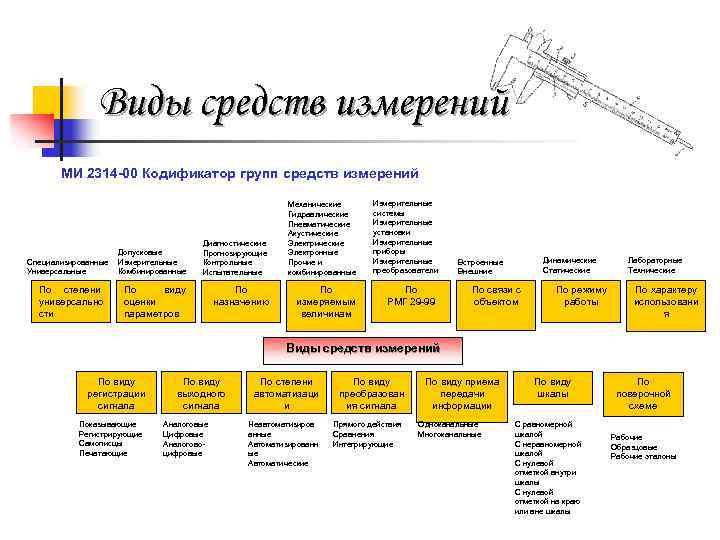
Виды средств измерений МИ 2314 -00 Кодификатор групп средств измерений Специализированные Универсальные По степени универсально сти Допусковые Измерительные Комбинированные Диагностические Прогнозирующие Контрольные Испытательные По виду оценки параметров По назначению Механические Гидравлические Пневматические Акустические Электронные Прочие и комбинированные По измеряемым величинам Измерительные системы Измерительные установки Измерительные приборы Измерительные преобразователи По РМГ 29 -99 Динамические Статические Встроенные Внешние По связи с объектом По режиму работы Лабораторные Технические По характеру использовани я Виды средств измерений По виду регистрации сигнала Показывающие Регистрирующие Самописцы Печатающие По виду выходного сигнала Аналоговые Цифровые Аналоговоцифровые По степени автоматизаци и Неавтоматизиров анные Автоматизированн ые Автоматические По виду преобразован ия сигнала Прямого действия Сравнения Интегрирующие По виду приема передачи информации Одноканальные Многоканальные По виду шкалы С равномерной шкалой С неравномерной шкалой С нулевой отметкой внутри шкалы С нулевой отметкой на краю или вне шкалы По поверочной схеме Рабочие Образцовые Рабочие эталоны
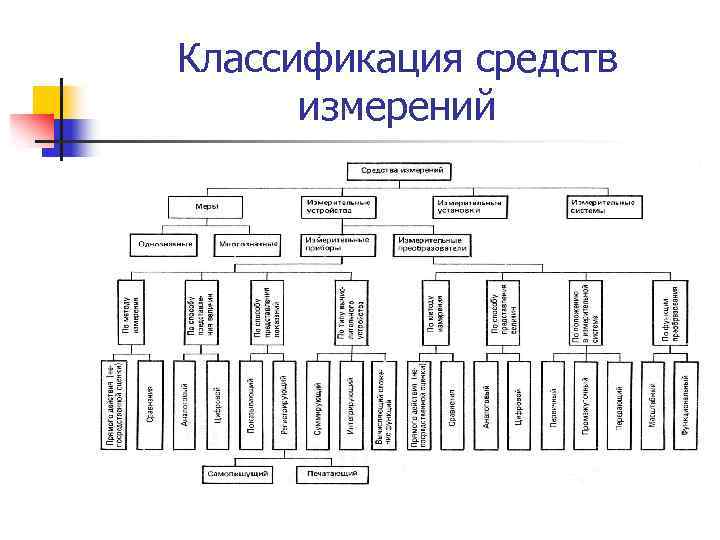
Классификация средств измерений
Классификация видов средств измерений МИ 2314 -00 Кодификатор групп средств измерений ТАБЛИЦЫ ГРУПП СИ ПО ВИДАМ И ОБЛАСТЯМ ИЗМЕРЕНИЙ 1. ИЗМЕРЕНИЯ ГЕОМЕТРИЧЕСКИХ ВЕЛИЧИН 2. ИЗМЕРЕНИЯ МЕХАНИЧЕСКИХ ВЕЛИЧИН 3. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ПОТОКА, РАСХОДА, УРОВНЯ, ОБЪЕМА ВЕЩЕСТВ 4. ИЗМЕРЕНИЯ ДАВЛЕНИЯ, ВАКУУМНЫЕ ИЗМЕРЕНИЯ 5. ИЗМЕРЕНИЯ ФИЗИКО-ХИМИЧЕСКОГО СОСТАВА И СВОЙСТВ ВЕЩЕСТВ 6. ТЕПЛОФИЗИЧЕСКИЕ И ТЕМПЕРАТУРНЫЕ ИЗМЕРЕНИЯ 7. ИЗМЕРЕНИЯ ВРЕМЕНИ И ЧАСТОТЫ 8. ИЗМЕРЕНИЯ ЭЛЕКТРОТЕХНИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН 9. РАДИОТЕХНИЧЕСКИЕ И РАДИОЭЛЕКТРОННЫЕ ИЗМЕРЕНИЯ 10. ВИБРОАКУСТИЧЕСКИЕ ИЗМЕРЕНИЯ 11. ОПТИЧЕСКИЕ И ОПТИКО-ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ 12. ИЗМЕРЕНИЯ ХАРАКТЕРИСТИК ИОНИЗИРУЮЩИХ ИЗЛУЧЕНИЙ И ЯДЕРНЫХ КОНСТАНТ 13. СИ МЕДИЦИНСКОГО НАЗНАЧЕНИЯ

По метрологическому назначению СИ подразделяются на 2 группы: - рабочие и - метрологические - эталоны (государственные и рабочие)

Рабочее СИ - средство измерений, предназначенное для измерений, не связанных с передачей размера единицы другим средствам измерений По условиям применения могут быть: - лабораторными; - производственными; - полевыми.

n Ученик – это не сосуд, который нужно наполнить, а огонь, который нужно зажечь.

По уровню автоматизации СИ подразделяются на 3 группы: - неавтоматические; - автоматизированные; - автоматические

Автоматическое СИ - Средство измерений, производящее без непосредственного участия человека измерения и все операции, связанные с обработкой результатов измерений, их регистрацией, передачей данных или выработкой управляющего сигнала.

Автоматизированное СИ - Средство измерений, производящее в автоматическом режиме одну или часть измерительных операций. Примеры: 1 Барограф (измерение и регистрация результатов). 2 Электрический счетчик электроэнергии (измерение и регистрация данных нарастающим итогом)

По уровню стандартизации СИ подразделяются на : - стандартизованные - нестандартизованные (уникальные)

Стандартизованное СИ - средство измерений, изготовленное и применяемое в соответствии с требованиями государственного или отраслевого стандарта. Серийно выпускаются промышленными предприятиями, в обязательном порядке подвергаются государственным испытаниям и заносятся в Государственном реестр.

Нестандартизованное СИ (НСИ) - средство измерений, стандартизация требований к которому признана нецелесообразной. Разрабатываются специализированными научно-исследовательскими организациями. Предназначены для решения специальной измерительной задачи. Выпускаются единичными экземплярами. Не проходят государственных испытаний, их характеристики определяются при метрологической аттестации

- Свои ошибки можно не исправлять, достаточно их учесть. n

Метрологическая характеристика СИ (МХ СИ) - характеристика одного из свойств средства измерений, влияющая на результат измерений и на его погрешность. Примечания 1 Для каждого типа средств измерений устанавливают свои метрологические характеристики. 2 МХ, устанавливаемые нормативно-техническими документами, называют нормируемыми МХ, а определяемые экспериментально – действительными МХ

Чувствительность СИ - свойство средства измерений, определяемое отношением изменения выходного сигнала этого средства (∆у) к вызывающему его изменению измеряемой величины (∆х) : S = ∆у/∆х

Порог чувствительности СИ - характеристика средства измерений в виде наименьшего значения изменения физической величины, начиная с которого может осуществляться ее измерение данным средством. Примечания 1 Если самое незначительное изменение массы, которое вызывает перемещение стрелки весов, составляет 10 мг, то порог чувствительности весов равен 10 мг. 2 На практике применяются также термины: реагирование и порог реагирования, подвижность средства измерений и порог подвижности, срабатывание и порог срабатывания. Иногда применяют термин пороговая чувствительность. Это свидетельствует о том, что терминология для выражения понятий, связанных со свойствами средства измерений реагировать на малые изменения измеряемых величин, еще не устоялась. В целях упорядочения терминологии эти термины следует рассматривать как синонимы и не применять их

Разрешение СИ - характеристика средства измерений, выражаемая наименьшим интервалом времени между отдельными импульсами или наименьшим расстоянием между объектами, которые фиксируются прибором раздельно. Примечание - Исходя из указанного определения различают временное разрешение и пространственное разрешение

Градуировочная характеристика СИ - зависимость между значениями величин на входе и выходе средства измерений, полученная экспериментально. Примечание - Градуированная характеристика может быть выражена в виде формулы, графика или таблицы

Метрологический отказ СИ - выход метрологической характеристики средства измерений за установленные пределы. Пример - Если погрешность средства измерений класса точности 0, 01 стала превышать 0, 01%, то это значит, что произошел метрологический отказ и средство измерений уже не соответствует установленному ранее классу точности. Если не установлены технические неполадки, то средству измерений может быть присвоен другой, более низкий класс точности.

n Любое устройство, требующее наладки и регулировки обычно не поддается ни тому, ни другому.
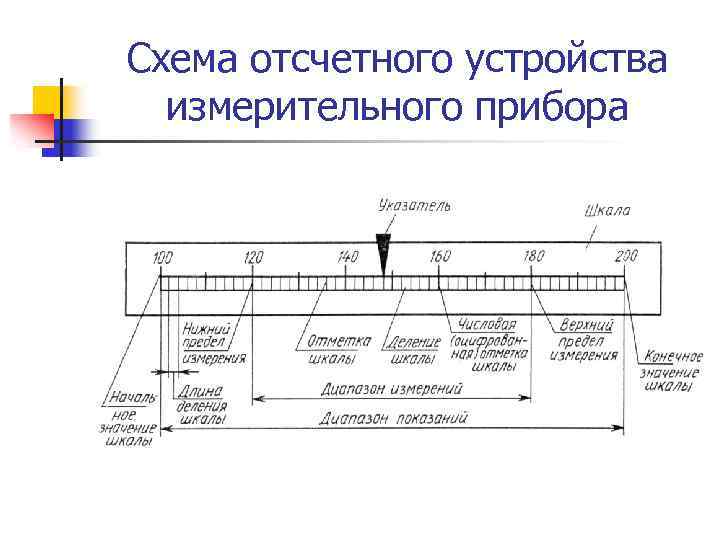
Схема отсчетного устройства измерительного прибора
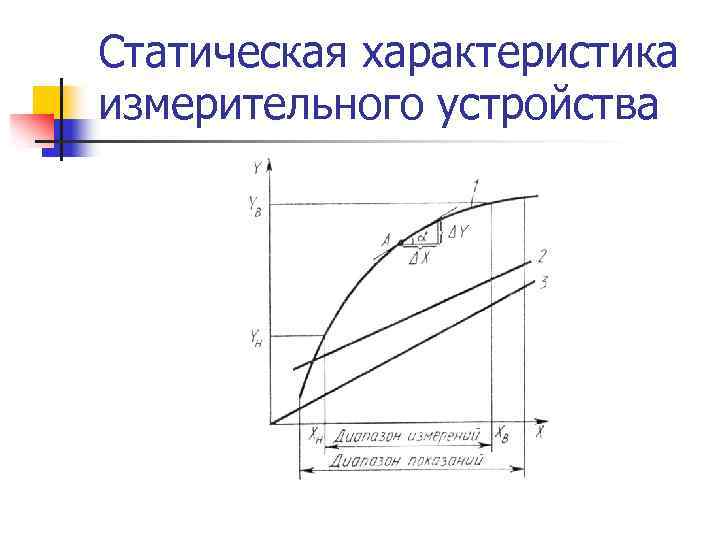
Статическая характеристика измерительного устройства
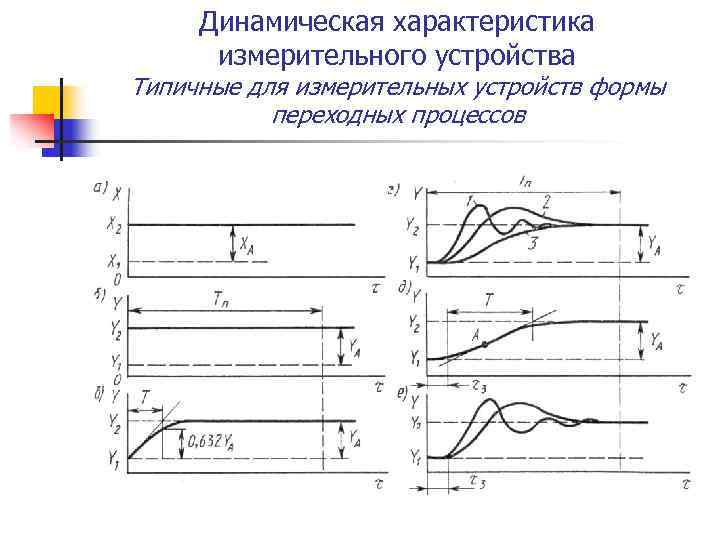
Динамическая характеристика измерительного устройства Типичные для измерительных устройств формы переходных процессов

Зона нечувствительности СИ - диапазон значений измеряемой величины, в пределах которого ее изменения не вызывают выходного сигнала средства измерений. Примечание - Иногда зону называют мертвой. Она наблюдается вблизи некоторых радионавигационных систем или измерительных установок. Например, зона нечувствительности у судовой радиолокационной установки, зависящая от размеров судна и высоты антенны радиолокационной установки над судовыми надстройками

n Любить без меры – неметрологично.
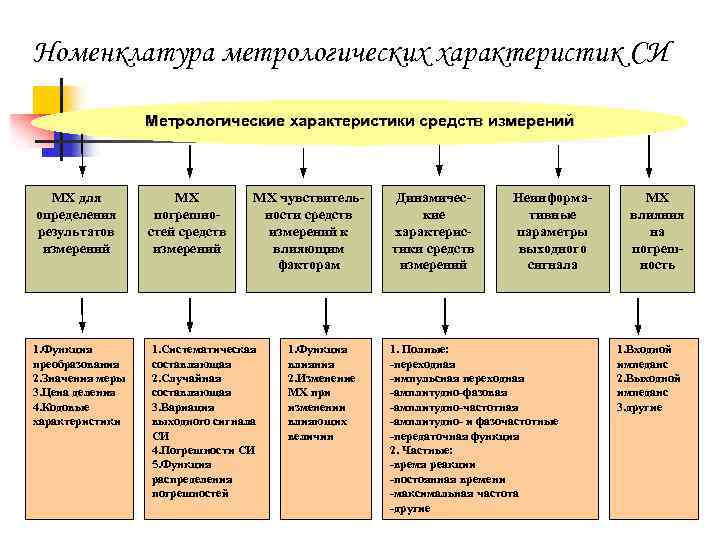
Номенклатура метрологических характеристик СИ Метрологические характеристики средств измерений МХ для определения результатов измерений 1. Функция преобразования 2. Значения меры 3. Цена деления 4. Кодовые характеристики МХ погрешностей средств измерений МХ чувствительности средств измерений к влияющим факторам 1. Систематическая составляющая 2. Случайная составляющая 3. Вариация выходного сигнала СИ 4. Погрешности СИ 5. Функция распределения погрешностей 1. Функция влияния 2. Изменение МХ при изменении влияющих величин Динамические характеристики средств измерений Неинформативные параметры выходного сигнала 1. Полные: -переходная -импульсная переходная -амплитудно-фазовая -амплитудно-частотная -амплитудно- и фазочастотные -передаточная функция 2. Частные: -время реакции -постоянная времени -максимальная частота -другие МХ влияния на погрешность 1. Входной импеданс 2. Выходной импеданс 3. другие

Нормирование МХ СИ установление границ на допустимые отклонения реальных МХ СИ от их номинальных значений.

Процедура нормирования: выбор комплекса МХ для типа СИ; n определение способов оценки МХ; n выбор способа представления МХ. n
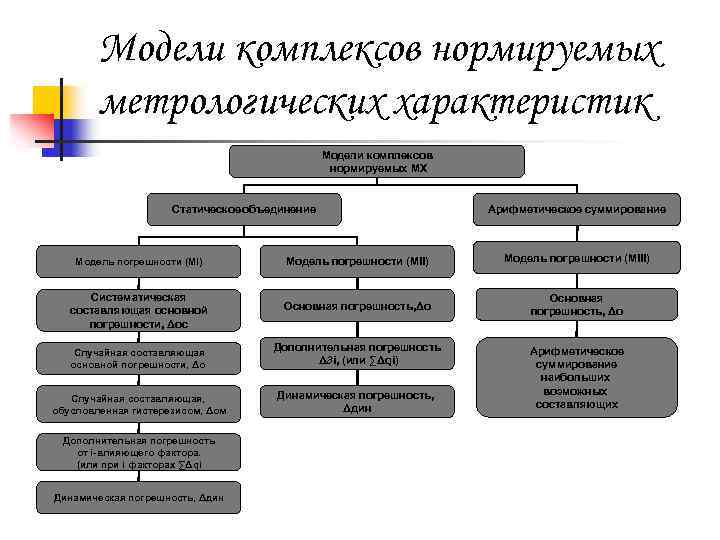
Модели комплексов нормируемых метрологических характеристик Модели комплексов нормируемых МХ Статическое объединение Арифметическое суммирование Модель погрешности (МI) Модель погрешности (МIII) Систематическая составляющая основной погрешности, Δос Основная погрешность, Δо Случайная составляющая основной погрешности, Δо Дополнительная погрешность Δ∂i, (или ∑Δqi) Случайная составляющая, обусловленная гистерезисом, Δом Динамическая погрешность, Δдин Дополнительная погрешность от i-влияющего фактора. (или при i факторах ∑Δqi Динамическая погрешность, Δдин Арифметическое суммирование наибольших возможных составляющих

Выводы: n n n Измерения являются неотъемлемой частью большинства трудовых процессов. Результаты измерений выражаются в узаконенных (установленных законодательством России) единицах; Значения показателей точности результатов измерений известны с необходимой заданной достоверностью; Значения показателей точности обеспечивают оптимальное в соответствии с выбранными критериями решение задачи, для которой эти результаты предназначены (результаты измерений получены с требуемой точностью). Метрологические свойства и метрологические характеристики являются основой всех измерений.

Погрешности измерений n Мелочи не играют решающей роли, они решают ВСЁ!
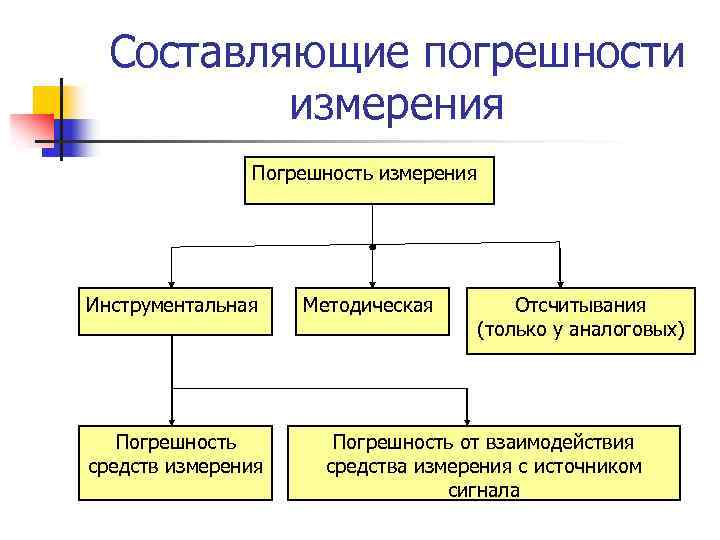
Составляющие погрешности измерения Погрешность измерения Инструментальная Погрешность средств измерения Методическая Отсчитывания (только у аналоговых) Погрешность от взаимодействия средства измерения с источником сигнала
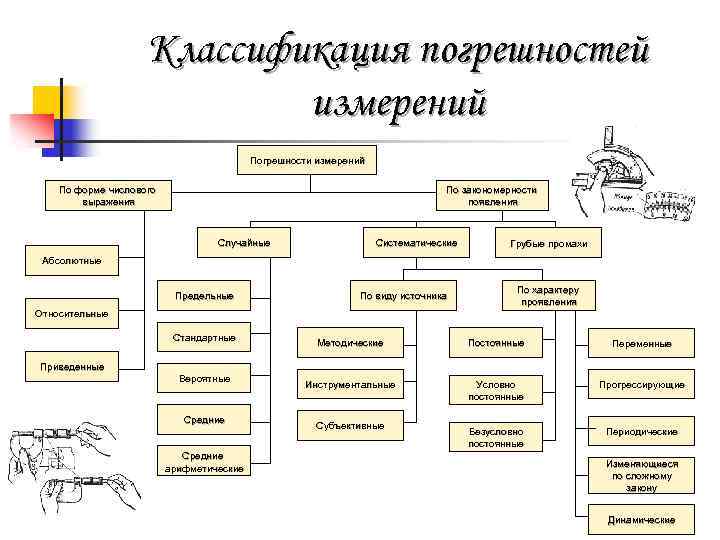
Классификация погрешностей измерений Погрешности измерений По форме числового выражения По закономерности появления Случайные Систематические Грубые промахи Абсолютные Предельные По виду источника По характеру проявления Относительные Стандартные Методические Постоянные Переменные Инструментальные Условно постоянные Прогрессирующие Безусловно постоянные Периодические Приведенные Вероятные Средние арифметические Субъективные Изменяющиеся по сложному закону Динамические

Математическое выражение погрешностей измерений n n Абсолютная погрешность – погрешность измерения, выраженная в единицах измеряемой величины: ∆ = х – х. Д Относительная погрешность – погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины, %: δ = ±(∆/ хд)*100%

n Приведенная (класс точности) – это отношение максимальной абсолютной погрешности прибора к пределу измерения величины:

Стандартизованный ряд значений для обозначения классов точности (n = 1, 0, -1, -2…).

Погрешность – это качественная мера нашего сомнения. n
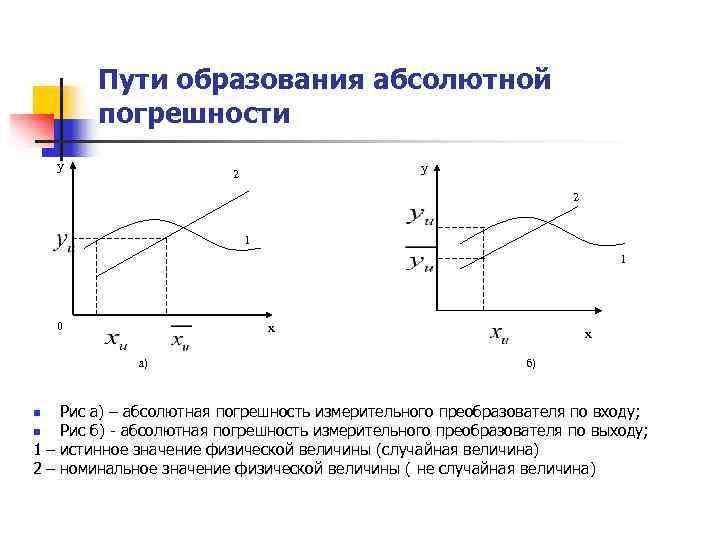
Пути образования абсолютной погрешности у у 2 2 1 1 0 х а) х б) Рис а) – абсолютная погрешность измерительного преобразователя по входу; n Рис б) - абсолютная погрешность измерительного преобразователя по выходу; 1 – истинное значение физической величины (случайная величина) 2 – номинальное значение физической величины ( не случайная величина) n
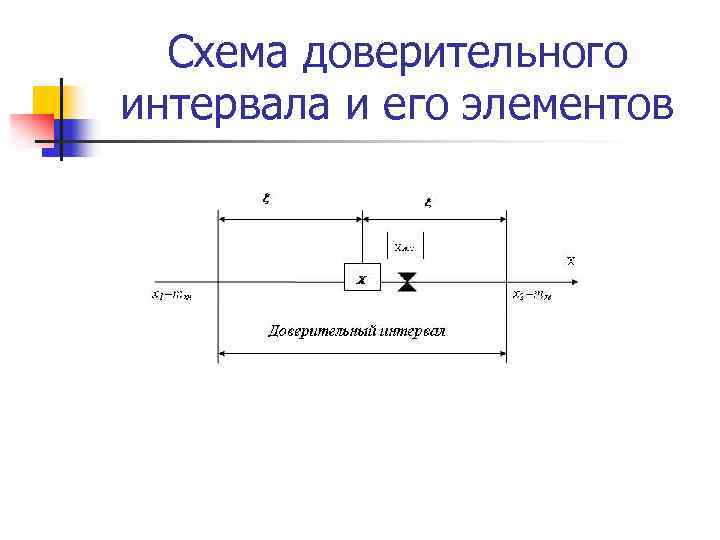
Схема доверительного интервала и его элементов
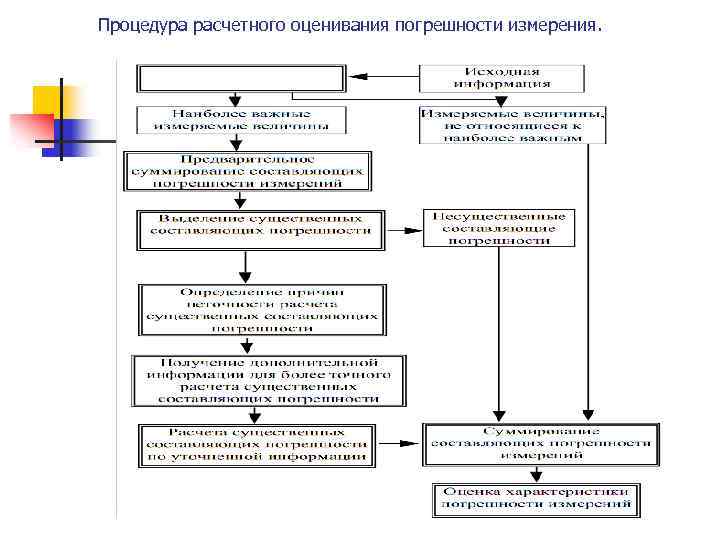
Процедура расчетного оценивания погрешности измерения.

Погрешность средства измерения Разность между показаниями средства измерения и истинным значением измеряемой величины.
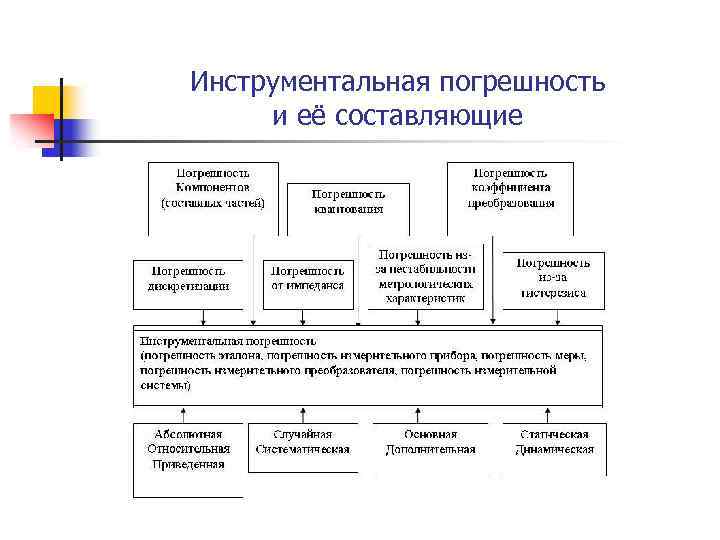
Инструментальная погрешность и её составляющие
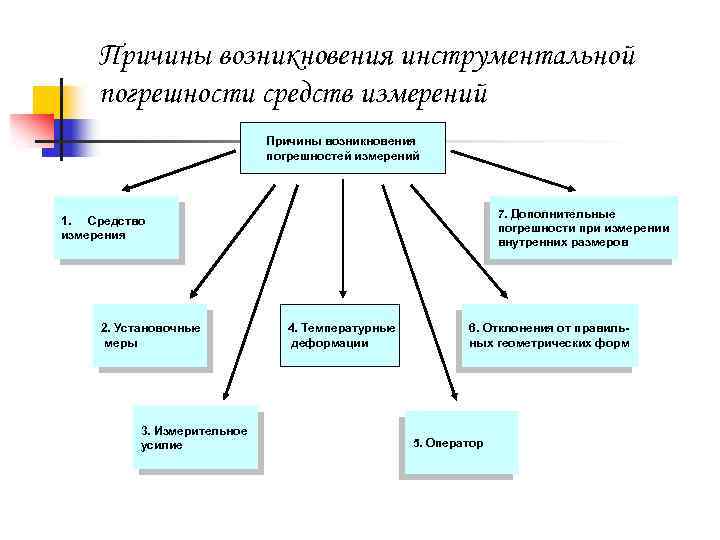
Причины возникновения инструментальной погрешности средств измерений Причины возникновения погрешностей измерений 7. Дополнительные погрешности при измерении внутренних размеров 1. Средство измерения 2. Установочные меры 3. Измерительное усилие 4. Температурные деформации 6. Отклонения от правильных геометрических форм 5. Оператор
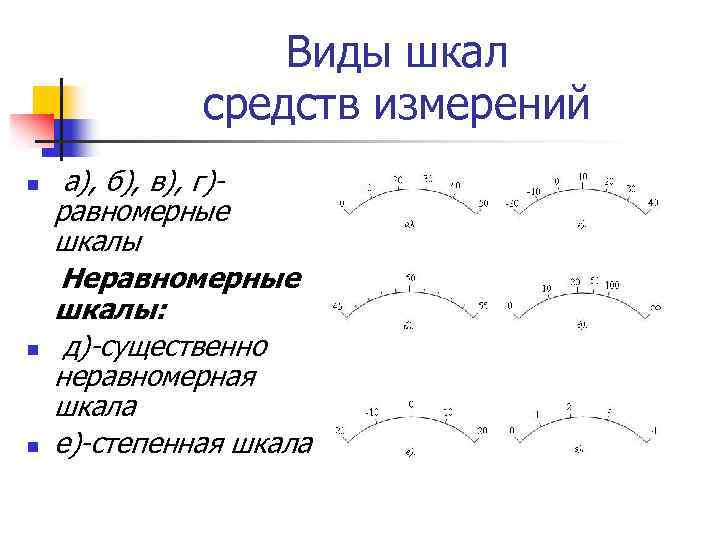
Виды шкал средств измерений n n n а), б), в), г)- равномерные шкалы Неравномерные шкалы: д)-существенно неравномерная шкала е)-степенная шкала
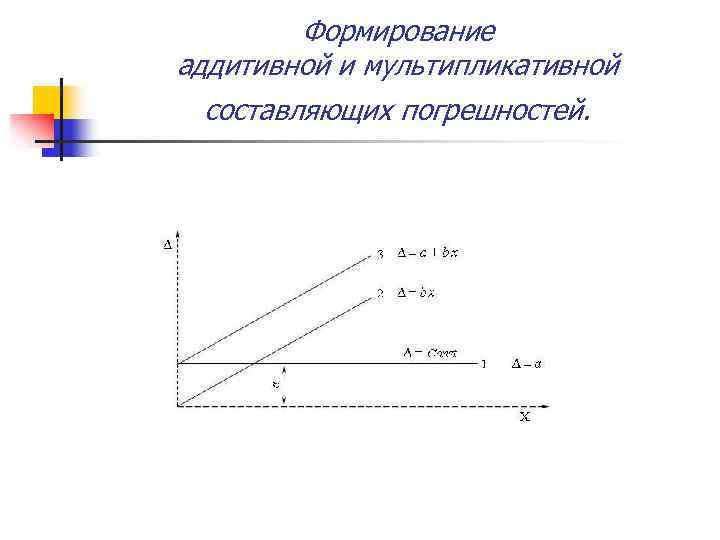
Формирование аддитивной и мультипликативной составляющих погрешностей.

Нормирование погрешностей с аддитивной и мультипликативной составляющими. n n n а). аддитивная; б). мультипликативная; в). аддитивная и мультипликативная.
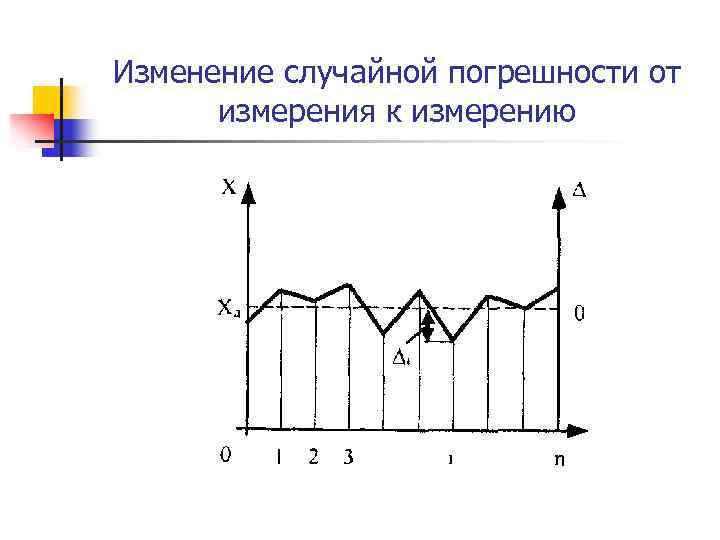
Изменение случайной погрешности от измерения к измерению

Истина – в большом числе измерений (стремящимся к бесконечности). n Если не хочешь иметь дело с погрешностью - никогда не повторяй измерения. n
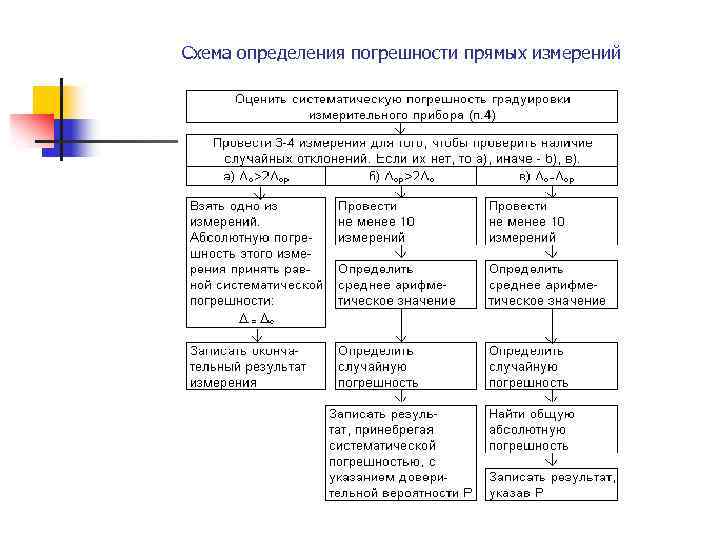
Схема определения погрешности прямых измерений

Изменение погрешности средств измерений во времени n n n . а)- модель изменения погрешности во времени, б) – плотность распределения времени наступления метрологических отказов, в) – вероятность безотказной работы, г) – зависимость интенсивности метрологических отказов от времени.

n Раньше метролог точно знал, что любой прибор грешит. Теперь он это тоже знает, но с некоторой неопределенностью.

Вероятностное описание ошибок наблюдения n n n Основные положения теории вероятности и математической статистики Законы распределения физических величин и их погрешностей Вероятностное суждение о законах распределения случайных величин

n „Каждое средство, способствующее точности наблюдений, может явиться средством будущего открытия. Мы должны искать наши будущие открытия в шестом десятичном знаке". Альберт Абрахам Майкельсон
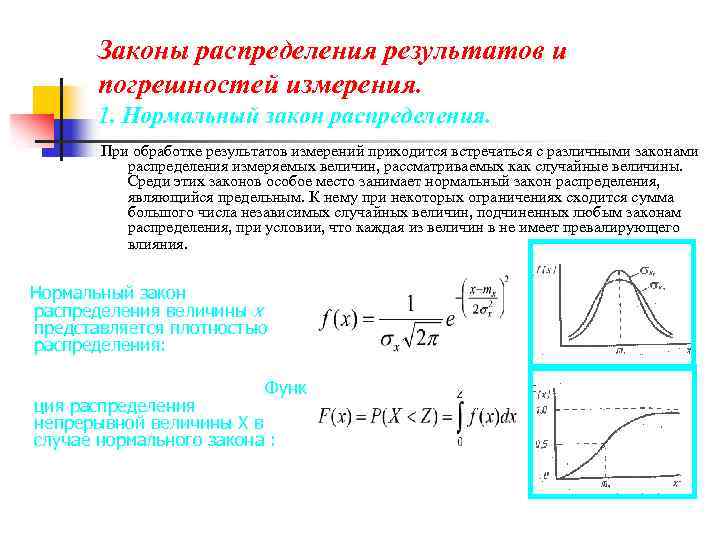
Законы распределения результатов и погрешностей измерения. 1. Нормальный закон распределения. При обработке результатов измерений приходится встречаться с различными законами распределения измеряемых величин, рассматриваемых как случайные величины. Среди этих законов особое место занимает нормальный закон распределения, являющийся предельным. К нему при некоторых ограничениях сходится сумма большого числа независимых случайных величин, подчиненных любым законам распределения, при условии, что каждая из величин в не имеет превалирующего влияния. Нормальный закон распределения величины х представляется плотностью распределения: Функ ция распределения непрерывной величины Х в случае нормального закона :
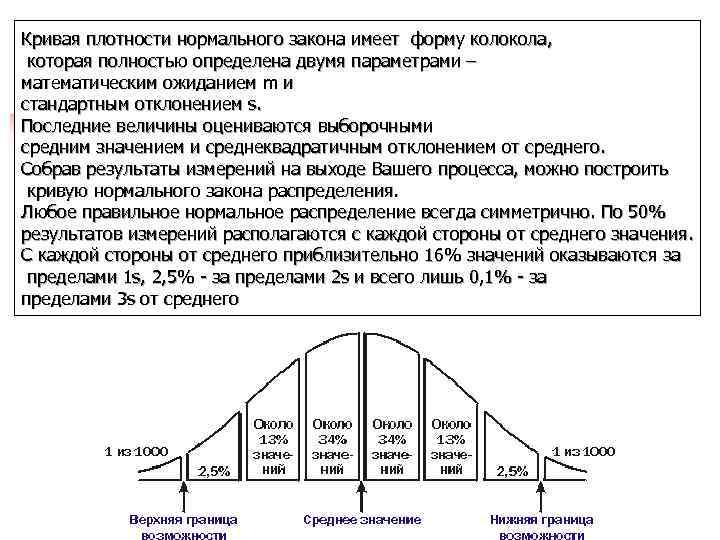
Кривая плотности нормального закона имеет форму колокола, которая полностью определена двумя параметрами – математическим ожиданием m и стандартным отклонением s. Последние величины оцениваются выборочными средним значением и среднеквадратичным отклонением от среднего. Собрав результаты измерений на выходе Вашего процесса, можно построить кривую нормального закона распределения. Любое правильное нормальное распределение всегда симметрично. По 50% результатов измерений располагаются с каждой стороны от среднего значения. С каждой стороны от среднего приблизительно 16% значений оказываются за пределами 1 s, 2, 5% - за пределами 2 s и всего лишь 0, 1% - за пределами 3 s от среднего

2. Равномерный закон распределения. В ряде случаев метрологической практики встречаются задачи, когда результаты измерений или их погрешности могут быть сосредоточены только в пределах заданного или известного из условий задачи интервала возможных значений величины. В данных случаях применяют равномерный закон распределения. Равномерный закон распределения величины х представляется плотностью распределения: Функ ция распределения непрерывной величины х в случае равномерного закона : Распространенными случаями применения равномерного закона распределения являются следующие. 1. Распределение неисключенных остатков систематической погрешности измерений выражается равномерным законом. 2. Секундные стрелки часов перемещаются скачкообразно. Если положение стрелки зафиксировано в положении т секунд, то истинный момент времени t является случайной величиной, имеющей значения с равной вероятностью от т до (т+1) секунды.

3. Арксинусный закон распределения. В некоторых случаях, связанных с регулировкой средств измерений при поверочных (калибровочных) работах, когда стремятся обеспечить нахождение значений погрешности средств измерений в пределах установленных допусков, значительная часть приборов имеет погрешности, группирующиеся к нижней и верхней границам поля допуска. Применяется арксинусный закон распределения. Арксинусный закон распределения величины х представляется плотностью распределения: Функ ция распределения непрерывной величины х в случае арксинусного закона :

4. Треугольный закон распределения (Симпсона). В некоторых случаях, чаще связанных с представлением распределения погрешностей измерений, используется треугольный закон распределения величины (закон Симпсона). Треугольный закон распределения величины х представляется плотностью распределения: Функ ция распределения непрерывной величины х в случае треугольного закона :

5. Корреляционный закон распределения. Опыт длительной эксплуатации многих типов сложных измерительных приборов показывает, что их погрешность после 3… 5 лет увеличивается, а закон распределения погрешностей и результатов измерений может значительно видоизмениться относительно начального периода эксплуатации. Данная функция распределения называется корреляционным распределением, поскольку позволяет учесть зависимость скорости изменения погрешности средств измерений в течение времени их эксплуатации от начального значения погрешности. Поэтому использование корреляционного распределения позволяет прогнозировать промежуток времени, в течение которого погрешности средства измерения в конкретных условиях не превзойдут предельно допускаемых. Функцию распределения предельных погрешностей средств измерений в зависимости от времени их эксплуатации t получим из условия, что вероятность : где М – допускаемый предельный уровень значения погрешности средства измерения.

n Логика приведёт Вас из пункта А в пункт В, воображение –куда угодно. n Альберт Эйнштейн

Представить выборку из 55 наблюдений в виде таблицы частот используя 7 интервалов группировки 17 19 23 18 21 15 16 13 20 18 15 20 14 20 16 14 20 19 15 19 16 15 22 21 12 10 21 18 14 17 18 13 19 18 20 24 20 19 17 18 19 21 17 19 17 13 17 11 18 19 17
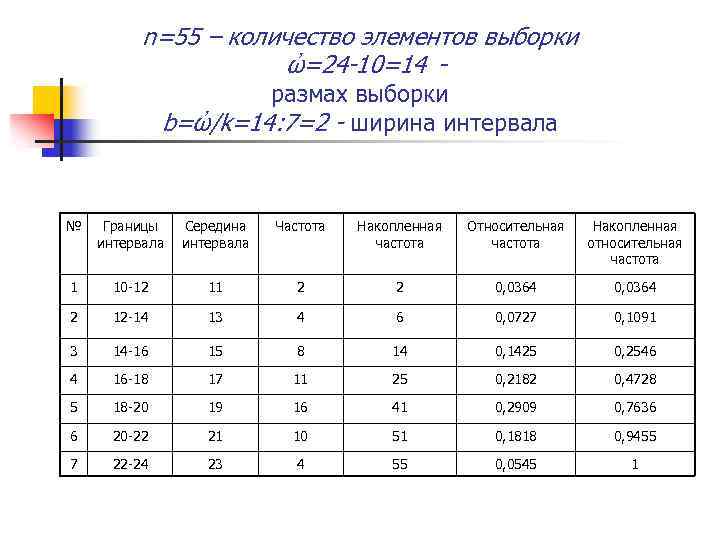
n=55 – количество элементов выборки ὠ=24 -10=14 размах выборки b=ὠ/k=14: 7=2 - ширина интервала № Границы интервала Середина интервала Частота Накопленная частота Относительная частота Накопленная относительная частота 1 10 -12 11 2 2 0, 0364 2 12 -14 13 4 6 0, 0727 0, 1091 3 14 -16 15 8 14 0, 1425 0, 2546 4 16 -18 17 11 25 0, 2182 0, 4728 5 18 -20 19 16 41 0, 2909 0, 7636 6 20 -22 21 10 51 0, 1818 0, 9455 7 22 -24 23 4 55 0, 0545 1

По результатам наблюдений можно представить выборку в виде полигона частот, гистограммы частот и эмпирической функции распределения. n n n Полигон частот даёт первое представление о законах распределения; Гистограмма частот – ступенчатая фигура, построенная на интервалах группировки таким образом, что площадь каждого прямоугольника равна частоте; Эмпирическая функция распределения определяется по накопленным относительным частотам.

Применение законов распределения. Пример 1: При проведении 500 опытов для нахождения абсолютной погрешности автоматического наведения радиотелескопа в заданную точку небесной сферы (в угловых секундах) получены результаты, сведенные в статистический ряд: -8; -6 -6; -4 -4; -2 -2; 0 0; +2 +2; +4 +4; +6 +6; +8 5 26 74 131 137 86 30 11 0, 010 0, 052 0, 148 0, 262 0, 274 0, 172 0, 060 0, 022 Требуется идентифицировать закон распределения погрешностей по данным статистического ряда одному из теоретических законов распределения и найти вероятность сходимости эмпирического и теоретического законов распределения. 1. Построим гистограмму как графическое представление статистической плотности распределения. Вид гистограммы на рис. 2. 1 свидетельствует о том, что возможной теоретической моделью данного распределения является нормальный закон, который и примем с целью идентификации. Гистограмма погрешности наведения радиотелескопа

2. Определим статистические оценки числовых параметров нормального распределения – математического ожидания m и дисперсии . Среднее арифметическое значение погрешности найдем по формуле где - среднее погрешности в i-м разряде. =(-7*0, 01)+(-5*0, 052)+(-3*0, 148)+(-1*0, 262)+1*0, 274)+ +(3*0, 172)+(5*0, 06)+(7*0, 022)=0, 208 угл. с. Статистическую дисперсию определим с помощью формулы Тогда (угл. с)2. Затем находим Статистическое СКО S=2, 78 угл. с.

3. Найдем теоретические вероятности попадания случайной величины в каждый из разрядов, используя таблицу функции Лапласа: р =0, 0526; р =0, 1493; р =0, 2573; р =0, 2668; р =0, 1742; р =0, 0681; 2 р8=0, 0162. 3 4 5 6 7 Сумма теоретических вероятностей должна быть равна 1. В примере , так как табличные аргументы функции Лапласа обычно позволяют учесть только два разряда после запятой.
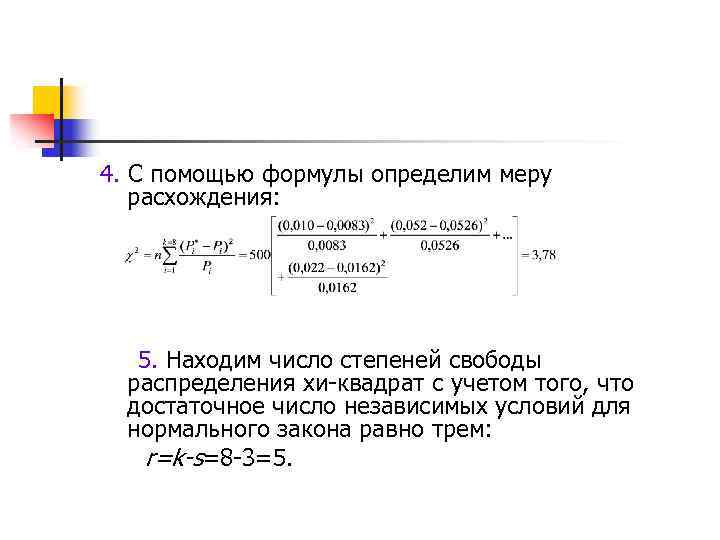
4. С помощью формулы определим меру расхождения: 5. Находим число степеней свободы распределения хи-квадрат с учетом того, что достаточное число независимых условий для нормального закона равно трем: r=k-s=8 -3=5.

6. Входим в таблицу Значения в зависимости от величин r, p и в соответствии с числами и r=5 определяем значение вероятности сходимости эмпирического и теоретического законов распределения , экстраполируя величину между «соседними» значениями таблицы 3, 00 и 4, 35. 7. Вероятность следует считать вполне достаточной для того, чтобы сделать уверенный вывод о том, что гипотеза о соответствии эмпирического закона нормальному закону распределения не противоречит полученным экспериментальным данным. Уверенности такого заключения, конечно, способствует тот факт, что информация о наблюдаемой погрешности наведения радиотелескопа достаточно состоятельна. Так, те же числовые характеристики, полученные всего по 50 измерениям, могли случайно дать столь хорошее совпадение распределений по критерию хи-квадрат, или, наоборот, могли привести к необходимости признания экспериментальных данных противоречащими гипотезе о нормальном законе распределения изучаемой величины. Ответ: Вероятность сходимости эмпирического и теоретического законов распределения , что говорит о соответствии эмпирического закона нормальному закону распределения.

Пример 2: Пусть имеется совокупность из N приборов, при этом вероятность исправности каждого прибора равна р. Требуется определить вероятность того, что исправных приборов не менее 2 -х и не более 4 -х, т. е. либо 2, либо 3.

Определим сначала вероятность того, что все первые испытанные приборы окажутся исправными. По теореме умножения вероятностей она будет равна , так как интересующее нас сложное событие состоит из х положительных исходов, вероятность каждого из которых р и N-x последующих отрицательных исходов, вероятность каждого из которых q=1 -p. Вероятность любой другой комбинации из x положительных и N-x отрицательных исходов будет . Число же таких комбинаций, как известно, равно числу сочетаний из N элементов по x: Вероятность обнаружить при испытании N приборов x исправных будет Данное распределение, ставящее в соответствие различным значениям x (при известных N, p, q) вероятность и появления, называется биномиальным.
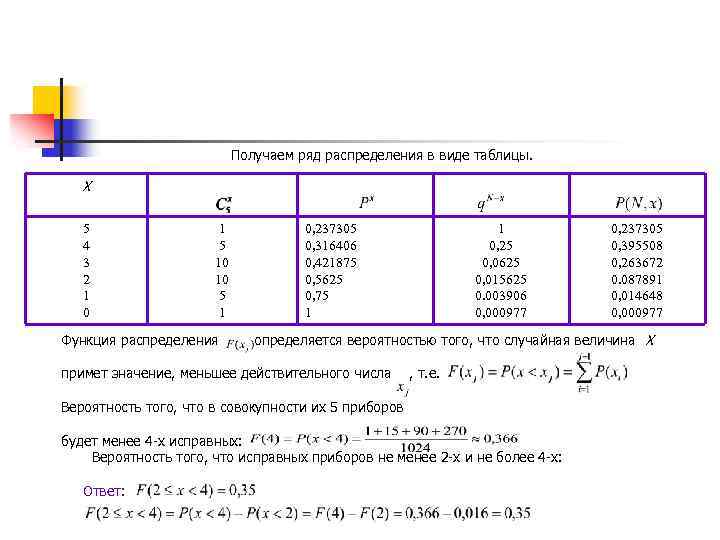
Получаем ряд распределения в виде таблицы. X 5 4 3 2 1 0 1 5 10 10 5 1 0, 237305 0, 316406 0, 421875 0, 5625 0, 75 1 1 0, 25 0, 0625 0, 015625 0. 003906 0, 000977 0, 237305 0, 395508 0, 263672 0. 087891 0, 014648 0, 000977 Функция распределения определяется вероятностью того, что случайная величина X примет значение, меньшее действительного числа , т. е. Вероятность того, что в совокупности их 5 приборов будет менее 4 -х исправных: Вероятность того, что исправных приборов не менее 2 -х и не более 4 -х: Ответ:

Заключение n n n Широкое распространение нормального распределения погрешностей и результатов измерений в практике объясняется центральной предельной теоремой теории вероятностей, являющейся одной из самых замечательных математических теорем. Центральная предельная теорема утверждает, что распределение случайных погрешностей будет близко в нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. Во многих случайных величинах, изучаемых в технике и других областях, естественно видеть суммарный аддитивный эффект большого числа независимых причин. Но центральное место нормального закона не следует объяснять его универсальной приложимостью. В этом смысле нормальный закон - один из многих типов распределения, имеющихся в природе, однако с относительно большим удельным весом практической приложимости. Однако полнота теоретических исследований, относящихся к нормальному и другим законам, а также сравнительно простые математические свойства делают их наиболее привлекательными и удобными в применении. Даже в случае отклонения исследуемых экспериментальных данных от нормального закона существует, по крайней мере, два пути его целесообразной эксплуатации: во-первых, использовать нормальный закон в качестве первого приближения, во-вторых, подобрать такое преобразование исследуемой случайной величины, которое видоизменяет исходный "не нормальный" закон распределения, превращая его в нормальный. Удобно для статистических приложений и свойство "самовоспроизводимости" нормального закона, заключающееся в том, что сумма любого числа нормально распределенных случайных величин тоже подчиняется нормальному закону распределения. Кроме того, с помощью закона нормального распределения выведен целый ряд других важных распределений, построены различные статистические критерии.

Методика обработки результатов измерений n n -Обработка результатов однократных наблюдений; -Обработка результатов многократных наблюдений; -Обработка результатов неравноточных рядов наблюдений; -Обработка результатов косвенных измерений

n Если за ошибку в расчете отвечает больше одного человека, виноватых не найти.
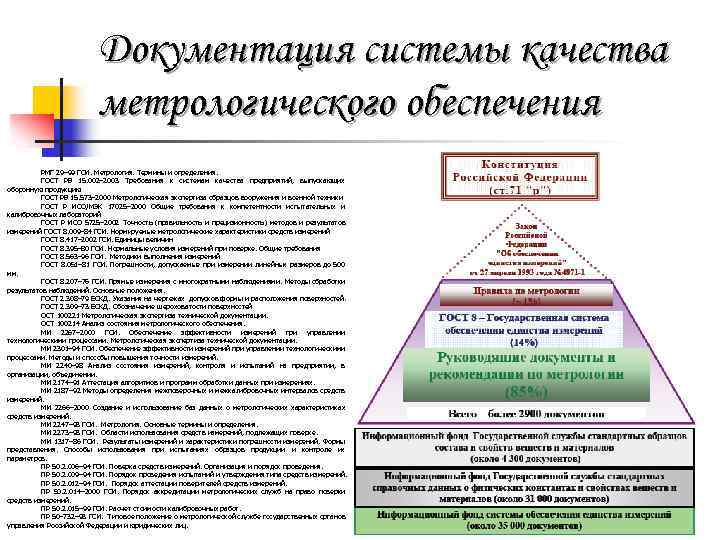
Документация системы качества метрологического обеспечения РМГ 29– 99 ГСИ. Метрология. Термины и определения. ГОСТ РВ 15. 002– 2003 Требования к системам качества предприятий, выпускающих оборонную продукцию ГОСТ РВ 15. 573– 2000 Метрологическая экспертиза образцов вооружения и военной техники ГОСТ Р ИСО/МЭК 17025– 2000 Общие требования к компетентности испытательных и калибровочных лабораторий ГОСТ Р ИСО 5725– 2002 Точность (правильность и прецизионность) методов и результатов измерений ГОСТ 8. 009– 84 ГСИ. Нормируемые метрологические характеристики средств измерений ГОСТ 8. 417– 2002 ГСИ. Единицы величин ГОСТ 8. 395– 80 ГСИ. Нормальные условия измерений при поверке. Общие требования ГОСТ 8. 563– 96 ГСИ. Методики выполнения измерений ГОСТ 8. 051– 81 ГСИ. Погрешности, допускаемые при измерении линейных размеров до 500 мм. ГОСТ 8. 207– 76 ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения. ГОСТ 2. 308– 79 ЕСКД. Указания на чертежах допусков формы и расположения поверхностей. ГОСТ 2. 309– 73 ЕСКД. Обозначение шероховатости поверхностей ОСТ 100221 Метрологическая экспертиза технической документации. ОСТ 100214 Анализ состояния метрологического обеспечения. МИ 2267– 2000 ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Метрологическая экспертиза технической документации. МИ 2301– 94 ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Методы и способы повышения точности измерений. МИ 2240– 98 Анализ состояния измерений, контроля и испытаний на предприятии, в организации, объединении. МИ 2174– 91 Аттестация алгоритмов и программ обработки данных при измерениях. МИ 2187– 92 Методы определения межповерочных и межкалибровочных интервалов средств измерений. МИ 2266– 2000 Создание и использование баз данных о метрологических характеристиках средств измерений. МИ 2247– 93 ГСИ. Метрология. Основные термины и определения. МИ 2273– 93 ГСИ. Области использования средств измерений, подлежащих поверке. МИ 1317– 86 ГСИ. Результаты измерений и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров. ПР 50. 2. 006– 94 ГСИ. Поверка средств измерений. Организация и порядок проведения. ПР 50. 2. 009– 94 ГСИ. Порядок проведения испытаний и утверждения типа средств измерений. ПР 50. 2. 012– 94 ГСИ. Порядок аттестации поверителей средств измерений. ПР 50. 2. 014– 2000 ГСИ. Порядок аккредитации метрологических служб на право поверки средств измерений. ПР 50. 2. 015– 99 ГСИ. Расчет стоимости калибровочных работ. ПР 50– 732– 93 ГСИ. Типовое положение о метрологической службе государственных органов управления Российской Федерации и юридических лиц.

Направления метрологического обеспечения
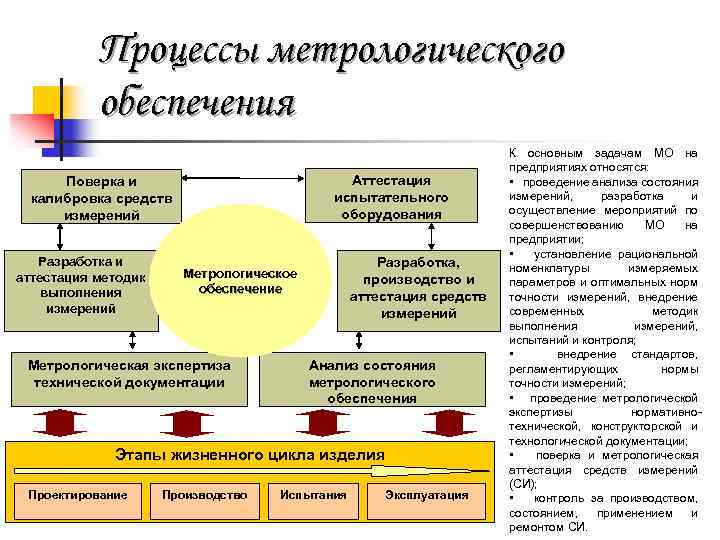
Процессы метрологического обеспечения Аттестация испытательного оборудования Поверка и калибровка средств измерений Разработка и аттестация методик выполнения измерений Разработка, производство и аттестация средств измерений Метрологическое обеспечение Метрологическая экспертиза технической документации Анализ состояния метрологического обеспечения Этапы жизненного цикла изделия Проектирование Производство Испытания Эксплуатация К основным задачам МО на предприятиях относятся: • проведение анализа состояния измерений, разработка и осуществление мероприятий по совершенствованию МО на предприятии; • установление рациональной номенклатуры измеряемых параметров и оптимальных норм точности измерений, внедрение современных методик выполнения измерений, испытаний и контроля; • внедрение стандартов, регламентирующих нормы точности измерений; • проведение метрологической экспертизы нормативнотехнической, конструкторской и технологической документации; • поверка и метрологическая аттестация средств измерений (СИ); • контроль за производством, состоянием, применением и ремонтом СИ.

Поверка и калибровка средств измерений ПР 50. 2. 006 -94 ПРАВИЛА ПО МЕТРОЛОГИИ. ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ. ПОРЯДОК ПРОВЕДЕНИЯ ПОВЕРКИ СРЕДСТВ ИЗМЕРЕНИЙ Поверка средств измерений - совокупность операций, выполняемых органами Государственной метрологической службы (другими уполномоченными органами, организациями) с целью определения и подтверждения соответствия средств измерений установленным техническим требованиям. ПР 50. 2. 016 - 94 ПРАВИЛА ПО МЕТРОЛОГИИ. ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ КАЛИБРОВОЧНЫХ РАБОТ Калибровка средства измерений (калибровочные работы) - совокупность операций, выполняемых с целью определения и подтверждения действительных значений метрологических характеристик и (или) пригодности к применению средства измерений, не подлежащего государственному метрологическому контролю и надзору. Статья 13. Закона «Об обеспечении единства измерений» Сферы распространения государственного метрологического контроля и надзора Государственный метрологический контроль и надзор, осуществляемые с целью проверки соблюдения метрологических правил и норм, распространяются на: • здравоохранение, ветеринарию, охрану окружающей среды, обеспечение безопасности труда; • торговые операции и взаимные расчеты между покупателем и продавцом, в том числе на операции с применением игровых автоматов и устройств; • государственные учетные операции; • обеспечение обороны государства; • геодезические и гидрометеорологические работы; • банковские, налоговые, таможенные и почтовые операции; • производство продукции, поставляемой по контрактам для государственных нужд в соответствии с законодательством РФ; • испытания и контроль качества продукции в целях определения соответствия обязательным требованиям государственных стандартов РФ; • обязательную сертификацию продукции и услуг; • измерения, проводимые по поручению органов суда, прокуратуры, арбитражного суда, государственных органов управления РФ; • регистрацию национальных и международных спортивных рекордов.
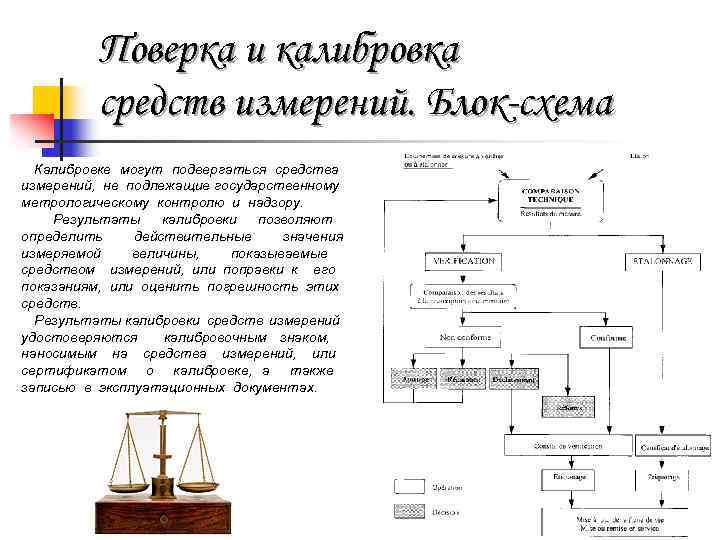
Поверка и калибровка средств измерений. Блок-схема Калибровке могут подвергаться средства измерений, не подлежащие государственному метрологическому контролю и надзору. Результаты калибровки позволяют определить действительные значения измеряемой величины, показываемые средством измерений, или поправки к его показаниям, или оценить погрешность этих средств. Результаты калибровки средств измерений удостоверяются калибровочным знаком, наносимым на средства измерений, или сертификатом о калибровке, а также записью в эксплуатационных документах.

Аттестация испытательного оборудования ГОСТ Р 8. 568 - 97 Государственная система обеспечения единства измерений. Аттестация испытательного оборудования. Основные положения Испытательное оборудование: средство испытаний, представляющее собой техническое устройство для воспроизведения условий испытаний Аттестация испытательного оборудования: определение нормированных точностных характеристик испытательного оборудования, их соответствия требованиям нормативных документов и установление пригодности этого оборудования к эксплуатации Основная цель аттестации испытательного оборудования - подтверждение возможности воспроизведения условий испытаний в пределах допускаемых отклонений и установление пригодности использования испытательного оборудования в соответствии с его назначением Для аттестации испытательного оборудования , используемого при обязательной сертификации продукции , при испытаниях продукции на соответствие обязательным требованиям государственных стандартов и производстве продукции , поставляемой по контрактам для государственных нужд , в том числе для нужд сферы обороны и безопасности, должны применяться средства измерений утвержденных типов , экземпляры средств измерений должны быть поверены, методики выполнения измерений должны быть аттестованы в соответствии с ГОСТ Р 8. 563. При аттестации испытательного оборудования для испытаний продукции, используемой в других сферах , должны применяться поверенные или калиброванные средства измерений

Разработка и аттестация методик выполнения измерений ГОСТ Р 8. 563 - 96 ГСИ. Методики выполнения измерений Методика выполнения измерений (МВИ) — совокупность операций и правил, выполнение которых обеспечивает получение результатов измерений с установленной погрешностью (неопределенностью ). МВИ, как правило, разрабатываются для сложных, комплексных измерений, на суммарную погрешность которых влияют несколько факторов

Разработка, производство и аттестация средств измерений • ОСТ 1 00231 -99 Отраслевая система обеспечения единства измерений. Средства измерений единичного изготовления • ОСТ 1 00405 -80 Отраслевая система обеспечения единства измерений. Средства измерений единичного производства. Общие требования к составлению контрольных образцов. Основные положения • ОСТ 1 00424 - 89 Отраслевая система единства измерения. Средства измерений единичного производства. Общие требования к составлению программ испытаний и аттестации • ОСТ 1 00427 - 81 Отраслевая система обеспечения единства измерений. Паспорт на нестандартизованные средства измерений • ОСТ 1 00441 - 82 Нестандартизованные средства измерений. Построение, содержание и утверждение технического задания на опытно-конструкторскую работу • ОСТ 1 00442 - 82 Отраслевая система обеспечения единства измерений. Технические условия на нестандартизованные средства измерений. Метрологические требования • ПР 50. 2. 009 - 94 Порядок проведения испытаний и утверждение типа средств измерений Метрологическая аттестация средств измерений – признание метрологической службой узаконенным для применения средств измерений единичного производства (или ввозимого единичными экземплярами из-за границы) на основании тщательных исследований его свойств.

Метрологическая экспертиза технической документации – это анализ и оценка технических решений по выбору параметров, подлежащих измерению, установлению норм точности измерений и обеспечению методами и средствами измерений процессов разработки, изготовления, испытаний и применения продукции.
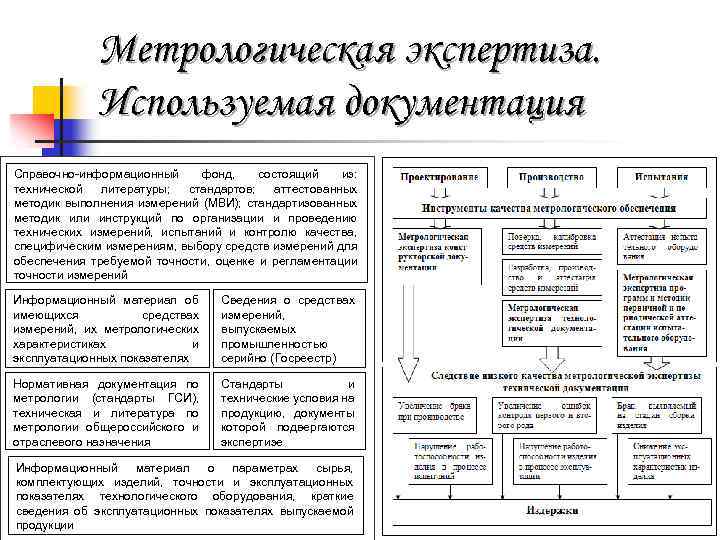
Метрологическая экспертиза. Используемая документация Справочно-информационный фонд, состоящий из: технической литературы; стандартов; аттестованных методик выполнения измерений (МВИ); стандартизованных методик или инструкций по организации и проведению технических измерений, испытаний и контролю качества, специфическим измерениям, выбору средств измерений для обеспечения требуемой точности, оценке и регламентации точности измерений Информационный материал об имеющихся средствах измерений, их метрологических характеристиках и эксплуатационных показателях Сведения о средствах измерений, выпускаемых промышленностью серийно (Госреестр) Нормативная документация по метрологии (стандарты ГСИ), техническая и литература по метрологии общероссийского и отраслевого назначения Стандарты и технические условия на продукцию, документы которой подвергаются экспертизе Информационный материал о параметрах сырья, комплектующих изделий, точности и эксплуатационных показателях технологического оборудования, краткие сведения об эксплуатационных показателях выпускаемой продукции

Анализ состояния метрологического обеспечения ОСТ 100214 Анализ состояния метрологического обеспечения Укомплектованность предприятия эталонами Укомплектованность предприятия СИ Укомплектованность предприятия СНК Интенсивность замены устаревших и внедрение новых эталонов Состояние выполнения графика поверки эталонов Объем ремонта эталонов, выполняемого на предприятии Состояние выполнения графика поверки (калибровки) СИ Объем ремонта СИ, выполняемого на предприятии Состояние выполнения графика поверки (калибровки) СНК Объем текстовой КД, охваченной МЭ и согласованной с отделом метрологом Объем графической КД, подвергнутой МЭ отделом метролога Объем графической КД, подвергнутой МЭ другими подразделениями Объем технологической документации, охваченной МЭ и согласованной с отделом метролога Объем карт техпроцессов, подвергнутых МЭ отделом метролога Объем карт техпроцессов, подвергнутых МЭ другими подразделениями Объем извещений об изменении, охваченных МЭ Оснащенность предприятия Kосн = 1/2, 5 * ( k 1+1, 5 k 2) Эффективность метрологического обеспечения Кэмо = 1/4, 5 * (1, 5 k 3+k 4+k 5) Эффективность метрологической экспертизы Кэмэ = 1/3 * (k 8+ k 9 + k 10) Общая оценка: Кобщ = 1/7 * (2 Kосн+2 Kэмо+3 Kэмэ)

Современные тенденции развития метрологии
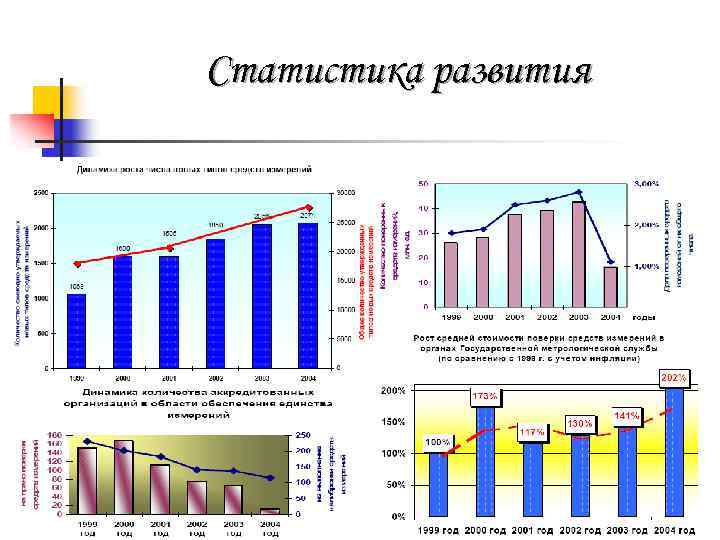
Статистика развития
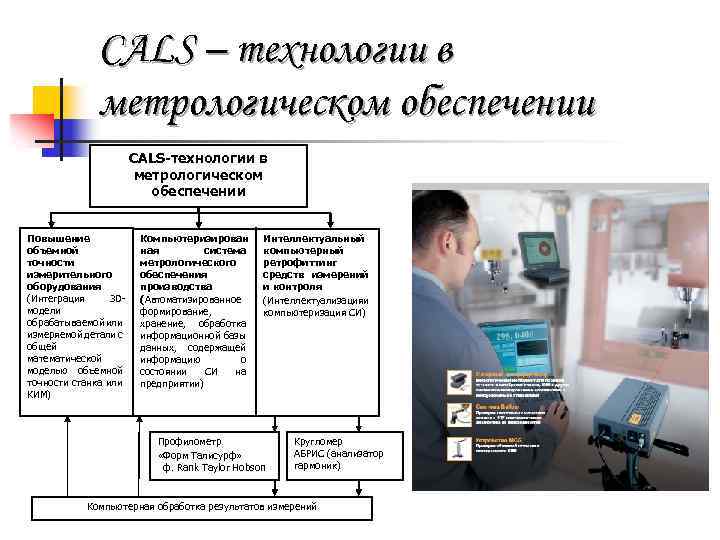
CALS – технологии в метрологическом обеспечении CALS-технологии в метрологическом обеспечении Повышение объемной точности измерительного оборудования (Интеграция 3 Dмодели обрабатываемой или измеряемой детали с общей математической моделью объемной точности станка или КИМ) Компьютеризирован ная система метрологического обеспечения производства (Автоматизированное формирование, хранение, обработка информационной базы данных, содержащей информацию о состоянии СИ на предприятии) Интеллектуальный компьютерный ретрофиттинг средств измерений и контроля (Интеллектуализация и компьютеризация СИ) Профилометр «Форм Талисурф» ф. Rank Taylor Hobson Кругломер АБРИС (анализатор гармоник) Компьютерная обработка результатов измерений
Автоматизация учета, хранения, управления, выбора СИ
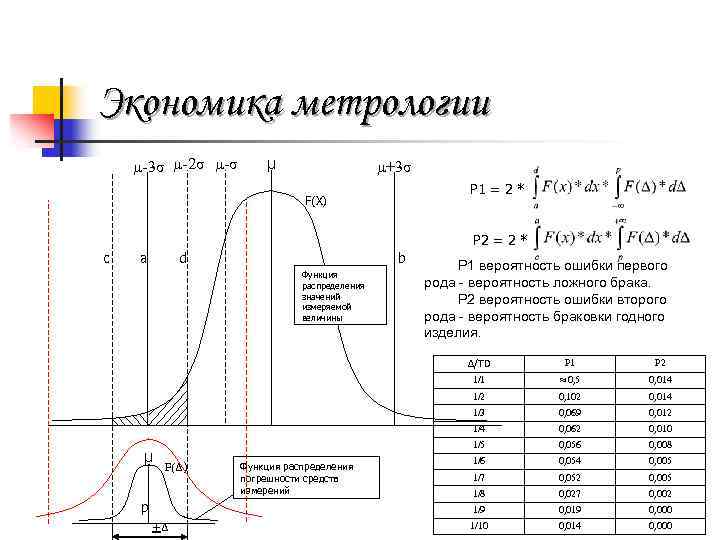
Экономика метрологии µ-3σ µ-2σ µ-σ µ µ+3σ P 1 = 2 * F(Х) P 2 = 2 * c а d b Функция распределения значений измеряемой величины Р 1 вероятность ошибки первого рода - вероятность ложного брака. Р 2 вероятность ошибки второго рода - вероятность браковки годного изделия. Δ/ТD 0, 014 0, 069 0, 012 0, 062 0, 010 1/5 0, 056 0, 008 1/6 0, 054 0, 005 1/7 0, 052 0, 005 1/8 0, 027 0, 002 1/9 +Δ 0, 102 1/4 p 0, 014 1/3 Функция распределения погрешности средств измерений ≈ 0, 5 1/2 F(Δ) Р 2 1/1 µ Р 1 0, 019 0, 000 1/10 0, 014 0, 000
Спасибо за внимание!
Lekcii po metrologii.ppt