Структура курса Основные понятия и определения эконометрики. Эконометрическое




























































































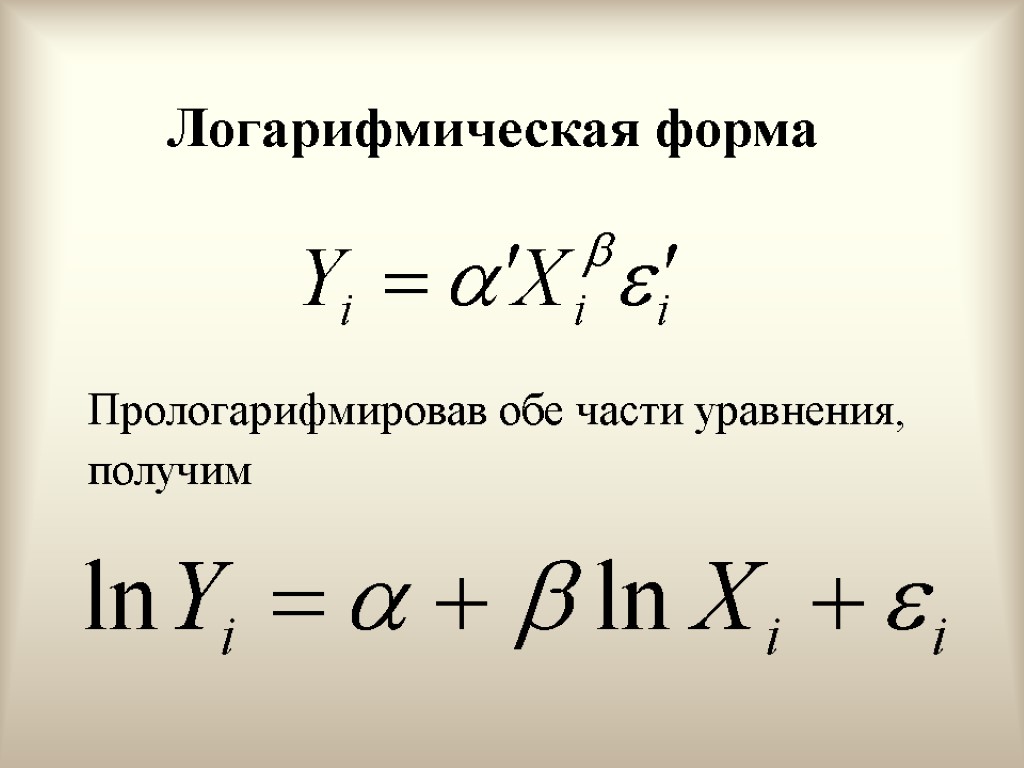











































































































































































































































ekonometrika_presentation.ppt
- Количество слайдов: 383
 Структура курса Основные понятия и определения эконометрики. Эконометрическое моделирование. Парная линейная регрессионная модель. Множественная линейная регрессионная модель. Статистические свойства МНК-оценок МЛРМ. Проверка гипотез относительно возможных значений коэффициентов МЛРМ. Мультиколлинеарность. Ошибки спецификации. Процедуры отбора регрессоров. Обобщенный метод наименьших квадратов Гетероскедастичность. Автокорреляция Прогнозирование при помощи МЛРМ. Временные ряды Системы одновременных уравнений
Структура курса Основные понятия и определения эконометрики. Эконометрическое моделирование. Парная линейная регрессионная модель. Множественная линейная регрессионная модель. Статистические свойства МНК-оценок МЛРМ. Проверка гипотез относительно возможных значений коэффициентов МЛРМ. Мультиколлинеарность. Ошибки спецификации. Процедуры отбора регрессоров. Обобщенный метод наименьших квадратов Гетероскедастичность. Автокорреляция Прогнозирование при помощи МЛРМ. Временные ряды Системы одновременных уравнений
 Необходимые требования и навыки Операции с векторами и матрицами. Дифференциальное и интегральное исчисление. Случайные величины. Функция распределения, закон распределения случайной величины Математическое ожидание, дисперсия, моменты распределения, ассиметрия, эксцесс. Нормальное распределение. Предельные теоремы и закон больших чисел. Статистическое оценивание неизвестных параметров. Точные и интервальные оценки. Состоятельность, эффективность, несмещенность оценок. Проверка статистических гипотез. Дисперсионный анализ.
Необходимые требования и навыки Операции с векторами и матрицами. Дифференциальное и интегральное исчисление. Случайные величины. Функция распределения, закон распределения случайной величины Математическое ожидание, дисперсия, моменты распределения, ассиметрия, эксцесс. Нормальное распределение. Предельные теоремы и закон больших чисел. Статистическое оценивание неизвестных параметров. Точные и интервальные оценки. Состоятельность, эффективность, несмещенность оценок. Проверка статистических гипотез. Дисперсионный анализ.
 Литература Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. (любое издание). Доугерти К. Введение в эконометрику. Москва, 2001. Эконометрика. Под ред. И. И. Елисеевой. Москва. Финансы и статистика, 2001. Практикум по эконометрике. Под ред. И. И. Елисеевой. Москва, финансы и статистика, 2001 Айвазян С. А., Мхитарян В. С. Прикладная статистика и основы эконометрики. Москва, Ю ЮНИТИ (любое издание). Кремер Н. Ш., Путко Б. А. Эконометрика. М. ЮНИТИ, 2002
Литература Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. (любое издание). Доугерти К. Введение в эконометрику. Москва, 2001. Эконометрика. Под ред. И. И. Елисеевой. Москва. Финансы и статистика, 2001. Практикум по эконометрике. Под ред. И. И. Елисеевой. Москва, финансы и статистика, 2001 Айвазян С. А., Мхитарян В. С. Прикладная статистика и основы эконометрики. Москва, Ю ЮНИТИ (любое издание). Кремер Н. Ш., Путко Б. А. Эконометрика. М. ЮНИТИ, 2002
 Тема 1. Эконометрическое моделирование Возникновение эконометрики как науки Определение эконометрики Прикладные цели эконометрики Этапы эконометрического моделирования
Тема 1. Эконометрическое моделирование Возникновение эконометрики как науки Определение эконометрики Прикладные цели эконометрики Этапы эконометрического моделирования
 История эконометрики как науки 1910, Австро-Венгрия – бухгалтер П. Цьемпа ввел термин «эконометрика» Цьемпа считал, что если к данным бухгалтерского учета применить методы алгебры и геометрии, то будет получено новое, более глубокое представление о результатах хозяйственной деятельности.
История эконометрики как науки 1910, Австро-Венгрия – бухгалтер П. Цьемпа ввел термин «эконометрика» Цьемпа считал, что если к данным бухгалтерского учета применить методы алгебры и геометрии, то будет получено новое, более глубокое представление о результатах хозяйственной деятельности.
 Современное определение эконометрики Эконометрика – научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе экономической теории; экономической статистики; математико-статистического инструментария придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией. (С. А. Айвазян, В. С. Мхитарян. Прикладная статистика и основы эконометрики.)
Современное определение эконометрики Эконометрика – научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе экономической теории; экономической статистики; математико-статистического инструментария придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией. (С. А. Айвазян, В. С. Мхитарян. Прикладная статистика и основы эконометрики.)
 Прикладные цели эконометрики вывод экономических законов; формулировка экономических моделей, основываясь на экономической теории и эмпирических данных; оценка неизвестных величин (параметров) в этих моделях; прогнозирование и оценка точности прогноза; выработка рекомендаций по экономической политике.
Прикладные цели эконометрики вывод экономических законов; формулировка экономических моделей, основываясь на экономической теории и эмпирических данных; оценка неизвестных величин (параметров) в этих моделях; прогнозирование и оценка точности прогноза; выработка рекомендаций по экономической политике.
 Этапы эконометрического моделирования Осознание того факта, что в экономике многие переменные связаны между собой Группировка отдельных соотношений в модель Сбор данных Идентификация Верификация
Этапы эконометрического моделирования Осознание того факта, что в экономике многие переменные связаны между собой Группировка отдельных соотношений в модель Сбор данных Идентификация Верификация
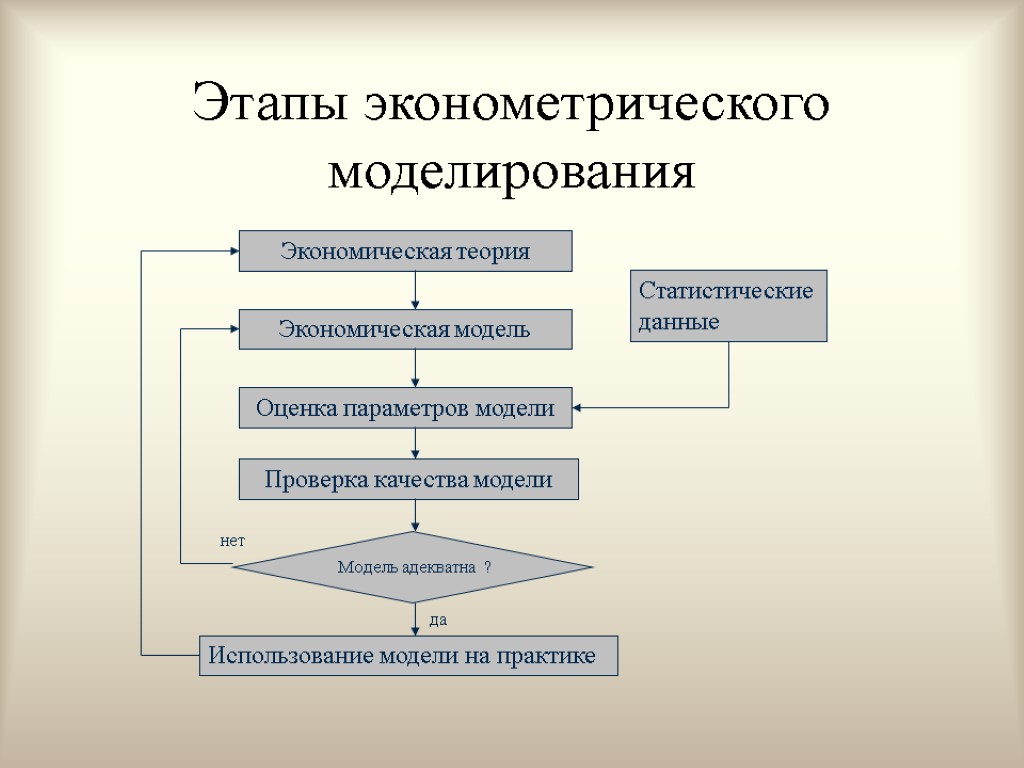
 Этапы эконометрического моделирования
Этапы эконометрического моделирования
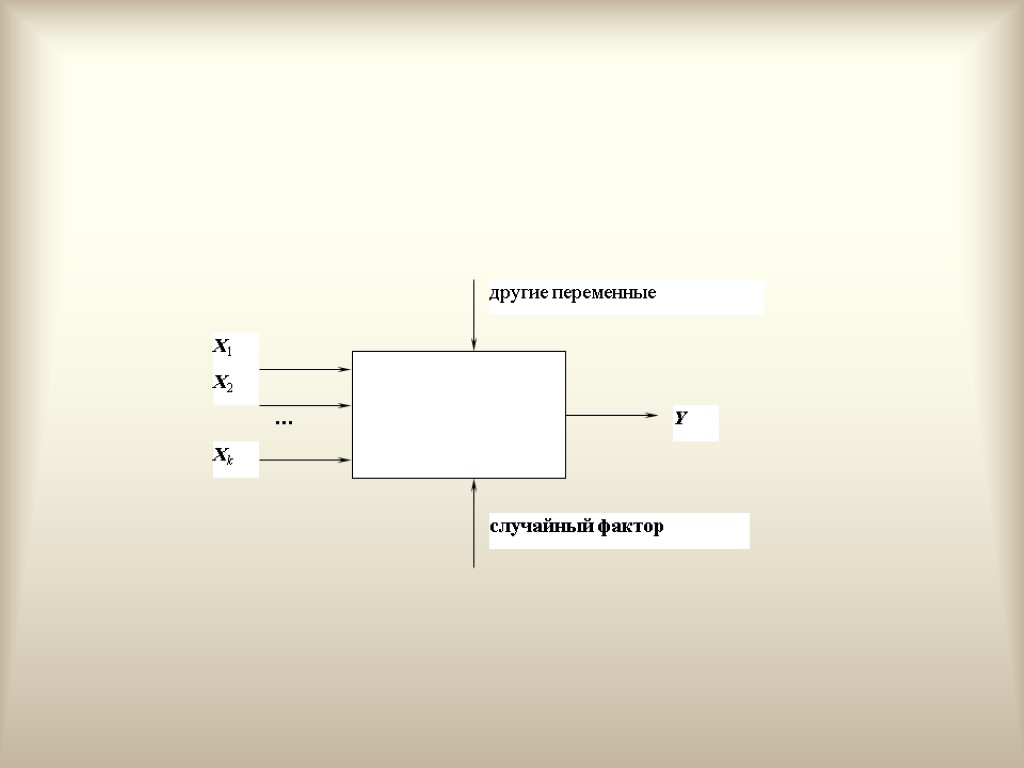
 1. Переменные модели Переменную, процесс формирования значений которой нас по каким-то причинам интересует, будем обозначать Y и называть зависимой или объясняемой. Переменные, которые, как мы предполагаем, оказывают влияние на переменную Y, будем обозначать Xj и называть независимыми или объясняющими.
1. Переменные модели Переменную, процесс формирования значений которой нас по каким-то причинам интересует, будем обозначать Y и называть зависимой или объясняемой. Переменные, которые, как мы предполагаем, оказывают влияние на переменную Y, будем обозначать Xj и называть независимыми или объясняющими.

 Другая классификация переменных Переменные, значения которых объясняются в рамках нашей модели, называются эндогенными. Переменные, значения которых нашей моделью не объясняются, являются для нее внешними, ничего о том, как формируются эти значения, мы не знаем, называются экзогенными
Другая классификация переменных Переменные, значения которых объясняются в рамках нашей модели, называются эндогенными. Переменные, значения которых нашей моделью не объясняются, являются для нее внешними, ничего о том, как формируются эти значения, мы не знаем, называются экзогенными
 2. Спецификация модели определение цели моделирования; определения списка экзогенных и эндогенных переменных; определение форм зависимостей между переменными; формулировка априорных ограничений на случайную составляющую, что важно для свойств оценок и выбора метода оценивания; формулировка априорных ограничений на коэффициенты
2. Спецификация модели определение цели моделирования; определения списка экзогенных и эндогенных переменных; определение форм зависимостей между переменными; формулировка априорных ограничений на случайную составляющую, что важно для свойств оценок и выбора метода оценивания; формулировка априорных ограничений на коэффициенты
 Виды эконометрических моделей Модели временных рядов. Регрессионные модели с одним уравнением. Системы одновременных уравнений.
Виды эконометрических моделей Модели временных рядов. Регрессионные модели с одним уравнением. Системы одновременных уравнений.
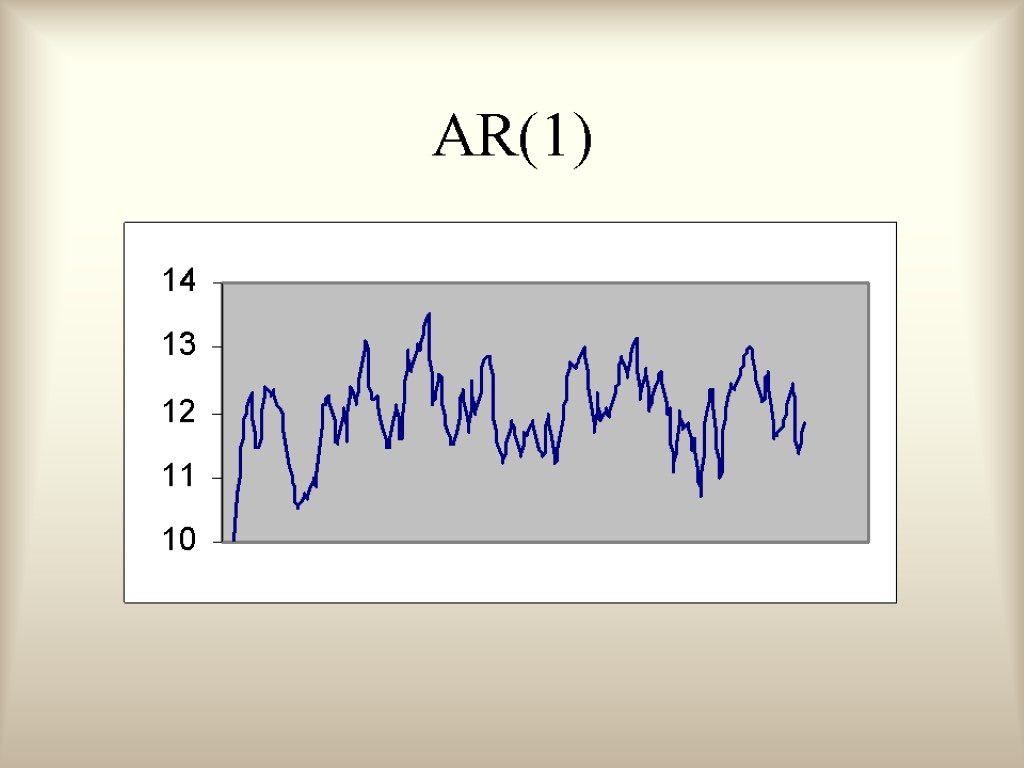
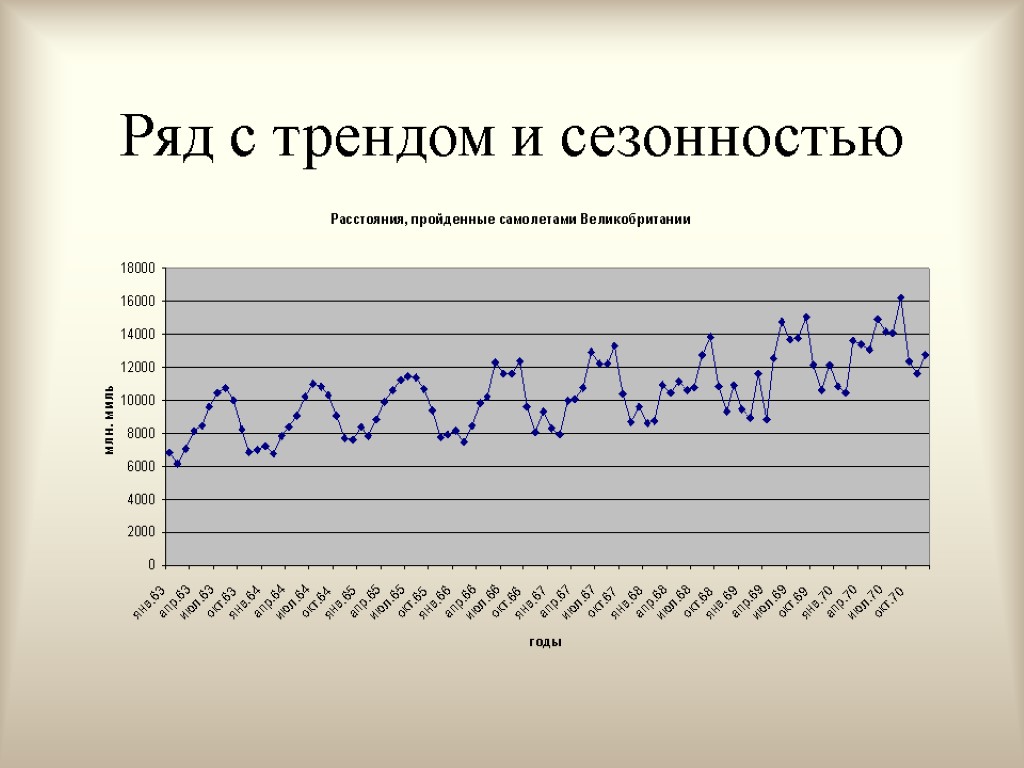
 Модели временных рядов. Такие модели объясняют поведение переменной, меняющейся с течением времени, исходя только из ее предыдущих значений. К этому классу относятся модели тренда, сезонности, тренда и сезонности (аддитивная и мультипликативная формы) и др.
Модели временных рядов. Такие модели объясняют поведение переменной, меняющейся с течением времени, исходя только из ее предыдущих значений. К этому классу относятся модели тренда, сезонности, тренда и сезонности (аддитивная и мультипликативная формы) и др.
 Регрессионные модели с одним уравнением. В таких моделях зависимая (объясняемая) переменная представляется в виде функции от независимых (объясняющих) переменных и параметров. В зависимости от вида функции модели бывают линейными и нелинейными.
Регрессионные модели с одним уравнением. В таких моделях зависимая (объясняемая) переменная представляется в виде функции от независимых (объясняющих) переменных и параметров. В зависимости от вида функции модели бывают линейными и нелинейными.
 Системы одновременных уравнений. Ситуация экономическая, поведение экономического объекта описывается системой уравнений. Системы состоят из уравнений и тождеств, которые могут содержать в себе объясняемые переменные из других уравнений (поэтому вводят понятия экзогенных и эндогенных переменных).
Системы одновременных уравнений. Ситуация экономическая, поведение экономического объекта описывается системой уравнений. Системы состоят из уравнений и тождеств, которые могут содержать в себе объясняемые переменные из других уравнений (поэтому вводят понятия экзогенных и эндогенных переменных).
 3. Сбор данных. cross-sectional data – пространственные данные – набор сведений по разным экономическим объектам в один и тот же момент времени; time-series data – временные ряды – наблюдение одного экономического параметра в разные периоды или моменты времени. Эти данные естественным образом упорядочены во времени. panel data – панельные данные – набор сведений по разным экономическим объектам за несколько периодов времени (данные переписи населения).
3. Сбор данных. cross-sectional data – пространственные данные – набор сведений по разным экономическим объектам в один и тот же момент времени; time-series data – временные ряды – наблюдение одного экономического параметра в разные периоды или моменты времени. Эти данные естественным образом упорядочены во времени. panel data – панельные данные – набор сведений по разным экономическим объектам за несколько периодов времени (данные переписи населения).
 4. Идентификация. Идентификация модели – статистический анализ модели и, прежде всего – статистическое оценивание параметров. Выбор метода оценивания сюда тоже входит. Зависит от особенностей модели.
4. Идентификация. Идентификация модели – статистический анализ модели и, прежде всего – статистическое оценивание параметров. Выбор метода оценивания сюда тоже входит. Зависит от особенностей модели.
 5. Верификация. Верификация модели – сопоставление реальных и модельных данных, проверка оцененной модели с тем, чтобы прийти к выводу о достаточной реалистичности получаемой с ее помощью картины объекта, либо признать необходимость оценки другой спецификации модели.
5. Верификация. Верификация модели – сопоставление реальных и модельных данных, проверка оцененной модели с тем, чтобы прийти к выводу о достаточной реалистичности получаемой с ее помощью картины объекта, либо признать необходимость оценки другой спецификации модели.
 Вопросы для самопроверки Кто первый ввел в употребление термин «Эконометрика». В каком году был основан журнал «Eсonometrics». Каких вы знаете лауреатов нобелевской премии по экономике за достижения в эконометрических методах. На каких «трех китах» базируется современная экономическая теория. Приведите определение эконометрики, отражающее современный взгляд на эту науку. Каковы прикладные цели эконометрики. Перечислите основные этапы эконометрического моделирования. Что входит в спецификацию модели. Что происходит на этапе идентификации модели. Какие основные типы экономических данных вы знаете. Основные типы эконометрических моделей. Как происходит верификация модели
Вопросы для самопроверки Кто первый ввел в употребление термин «Эконометрика». В каком году был основан журнал «Eсonometrics». Каких вы знаете лауреатов нобелевской премии по экономике за достижения в эконометрических методах. На каких «трех китах» базируется современная экономическая теория. Приведите определение эконометрики, отражающее современный взгляд на эту науку. Каковы прикладные цели эконометрики. Перечислите основные этапы эконометрического моделирования. Что входит в спецификацию модели. Что происходит на этапе идентификации модели. Какие основные типы экономических данных вы знаете. Основные типы эконометрических моделей. Как происходит верификация модели
 Тема 2. Парная линейная регрессионная модель ПЛРМ
Тема 2. Парная линейная регрессионная модель ПЛРМ
 Две переменные X и Y могут быть связаны функциональной зависимостью (т.е. существует функция f что Y = f(X), значения переменной Y полностью определяются значениями переменной X) статистической зависимостью независимы.
Две переменные X и Y могут быть связаны функциональной зависимостью (т.е. существует функция f что Y = f(X), значения переменной Y полностью определяются значениями переменной X) статистической зависимостью независимы.
 Статистическая зависимость Если при изменении X меняется закон распределения случайной величины Y, то говорят, что величины (X,Y) связаны статистической зависимостью. Статистическая зависимость называется корреляционной, если при изменении X меняется математическое ожидание случайной величины Y.
Статистическая зависимость Если при изменении X меняется закон распределения случайной величины Y, то говорят, что величины (X,Y) связаны статистической зависимостью. Статистическая зависимость называется корреляционной, если при изменении X меняется математическое ожидание случайной величины Y.
 Корреляционная зависимость Если каждому значению величины X соответствует свое значение то говорят, что существует регрессионная функция
Корреляционная зависимость Если каждому значению величины X соответствует свое значение то говорят, что существует регрессионная функция
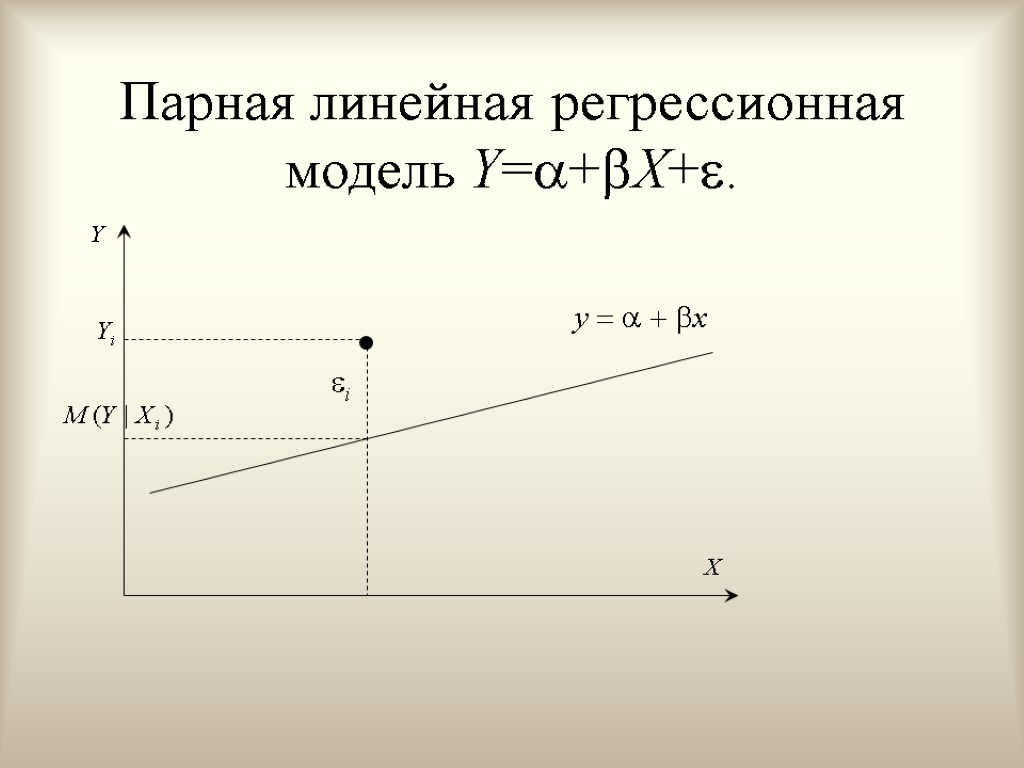
 Случайная составляющая Отклонение переменной Y от математического ожидания для соответствующего значения переменной X называется ошибкой и обозначается
Случайная составляющая Отклонение переменной Y от математического ожидания для соответствующего значения переменной X называется ошибкой и обозначается
 Регрессионное уравнение Уравнение называется уравнением регрессии переменной Y на переменную X
Регрессионное уравнение Уравнение называется уравнением регрессии переменной Y на переменную X
 Экономический смысл невключение объясняющих переменных в уравнение. На самом деле на переменную Y влияет не только переменная X, но и ряд других переменных, которые не учтены в нашей модели по следующим причинам: мы знаем, что другая переменная влияет, но не модем ее учесть, потому как не знаем, как измерить (психологический фактор, например); существуют факторы, которые мы знаем, как измерить, но влияние их на Y так слабо, что их не стоит учитывать; существенные переменные, но из-за отсутствия опыта или знаний мы их таковыми не считаем.
Экономический смысл невключение объясняющих переменных в уравнение. На самом деле на переменную Y влияет не только переменная X, но и ряд других переменных, которые не учтены в нашей модели по следующим причинам: мы знаем, что другая переменная влияет, но не модем ее учесть, потому как не знаем, как измерить (психологический фактор, например); существуют факторы, которые мы знаем, как измерить, но влияние их на Y так слабо, что их не стоит учитывать; существенные переменные, но из-за отсутствия опыта или знаний мы их таковыми не считаем.
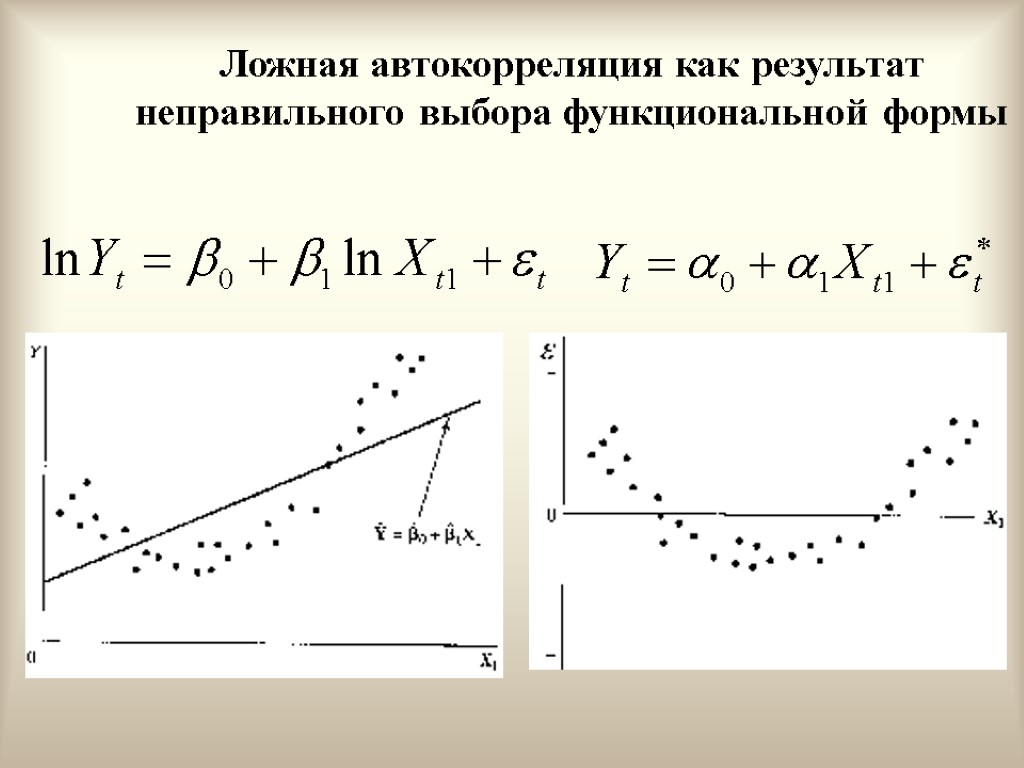
 Экономический смысл (продолжение) Неправильная функциональная спецификация. Функциональное соотношение между Y и Х может быть определено неправильно. Например, мы предположили линейную зависимость, а она может быть более сложной. Ошибки наблюдений (занижение реального уровня доходов). В этом случае наблюдаемые значения не будут соответствовать точному соотношению, и существующее расхождение будет вносить свой вклад в остаточный член.
Экономический смысл (продолжение) Неправильная функциональная спецификация. Функциональное соотношение между Y и Х может быть определено неправильно. Например, мы предположили линейную зависимость, а она может быть более сложной. Ошибки наблюдений (занижение реального уровня доходов). В этом случае наблюдаемые значения не будут соответствовать точному соотношению, и существующее расхождение будет вносить свой вклад в остаточный член.
 Способы определения регрессионной функции f(X) параметрический – предполагаем, что вид регрессионной функции известен, неизвестны параметры функции непараметрический – предполагаем, что вид регрессионной функции неизвестен и мы составляем алгоритм расчета значений функции в каждой точке
Способы определения регрессионной функции f(X) параметрический – предполагаем, что вид регрессионной функции известен, неизвестны параметры функции непараметрический – предполагаем, что вид регрессионной функции неизвестен и мы составляем алгоритм расчета значений функции в каждой точке
 Выбор вида f(X) экономическая теория опыт, интуиция исследователя эмпирический анализ данных
Выбор вида f(X) экономическая теория опыт, интуиция исследователя эмпирический анализ данных
 Эмпирический анализ данных В парном случае материал наблюдений представляет собой набор пар чисел: .
Эмпирический анализ данных В парном случае материал наблюдений представляет собой набор пар чисел: .
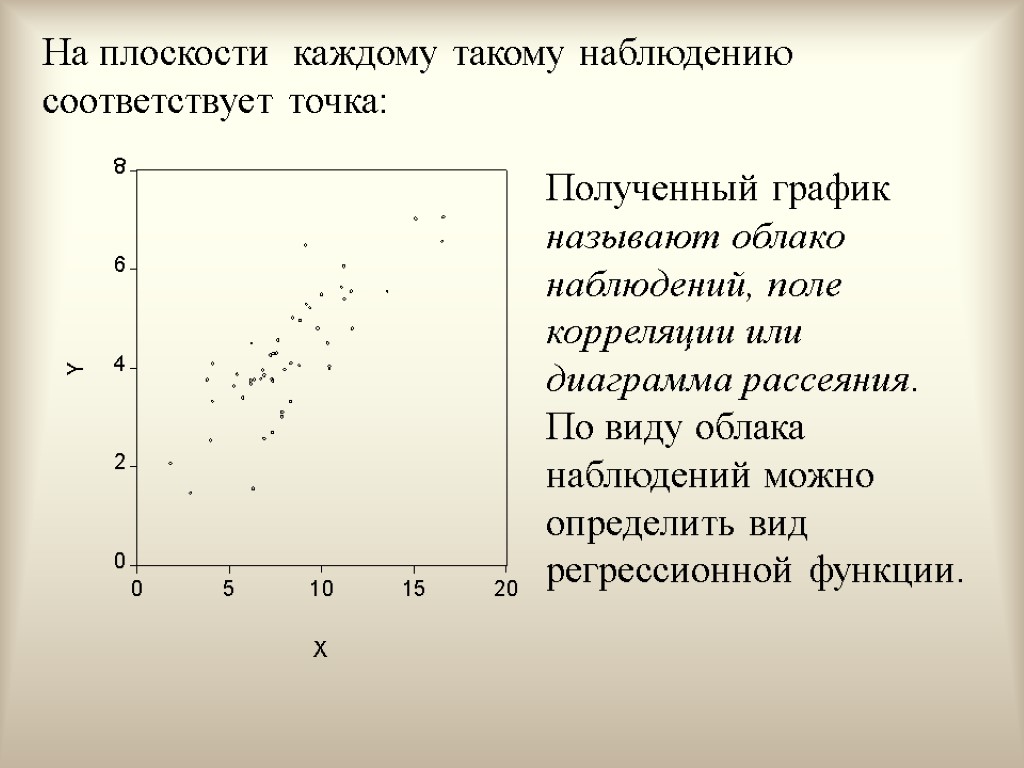
 На плоскости каждому такому наблюдению соответствует точка: Полученный график называют облако наблюдений, поле корреляции или диаграмма рассеяния. По виду облака наблюдений можно определить вид регрессионной функции.
На плоскости каждому такому наблюдению соответствует точка: Полученный график называют облако наблюдений, поле корреляции или диаграмма рассеяния. По виду облака наблюдений можно определить вид регрессионной функции.
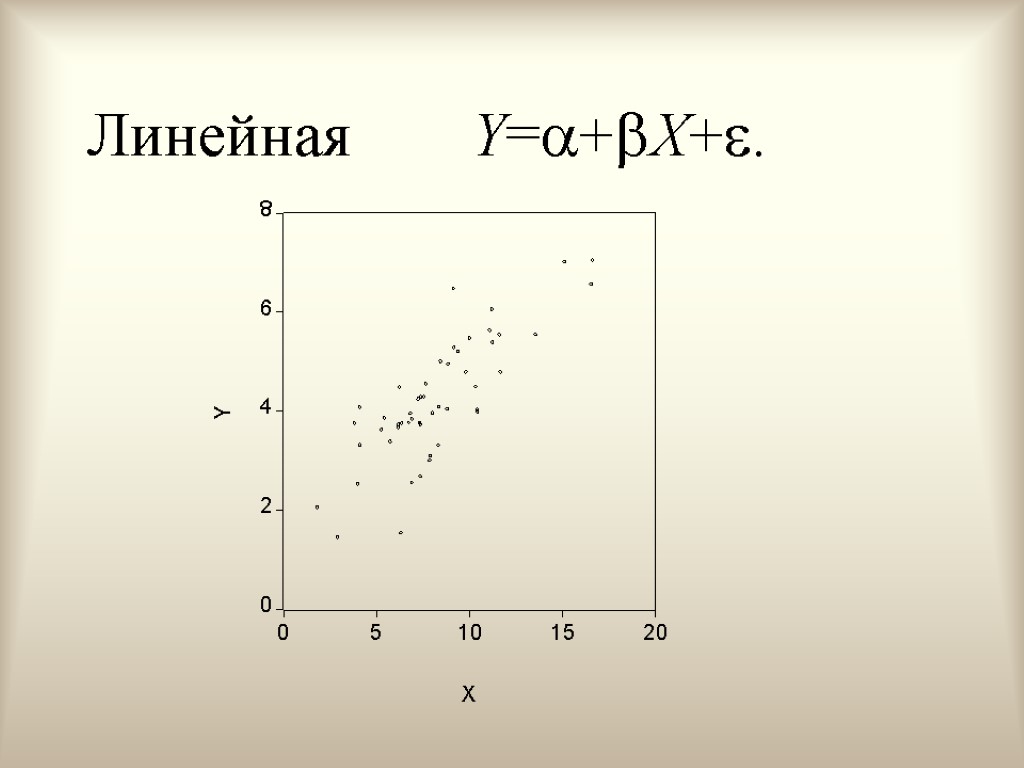
 Линейная Y=+X+.
Линейная Y=+X+.
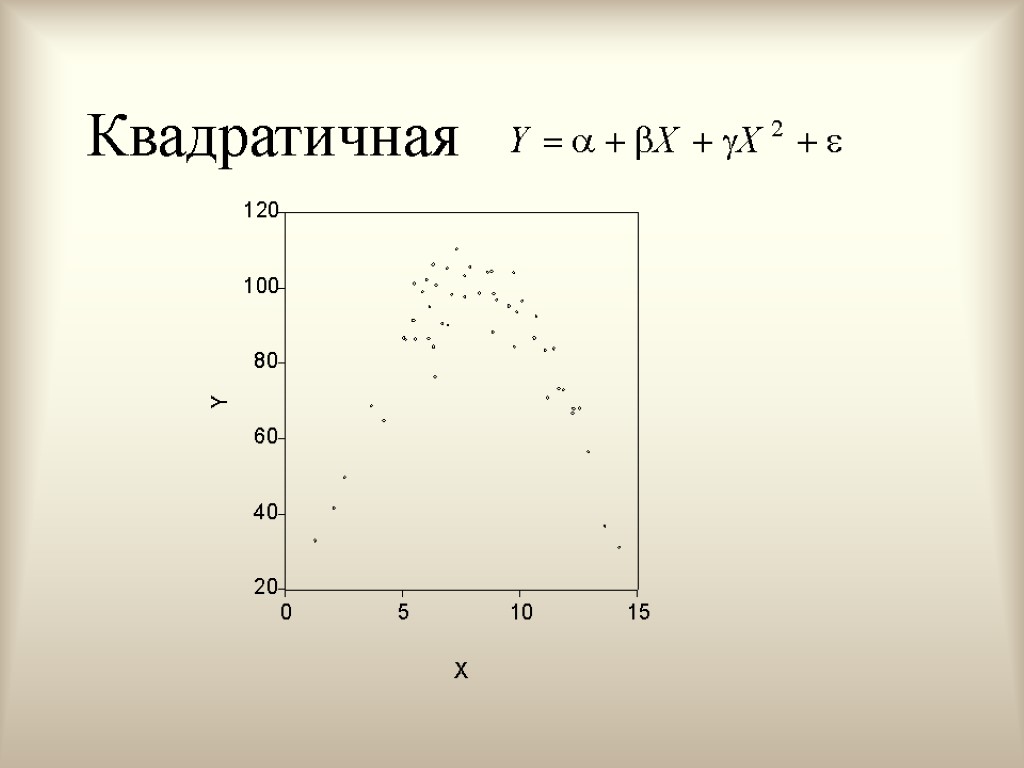
 Квадратичная
Квадратичная
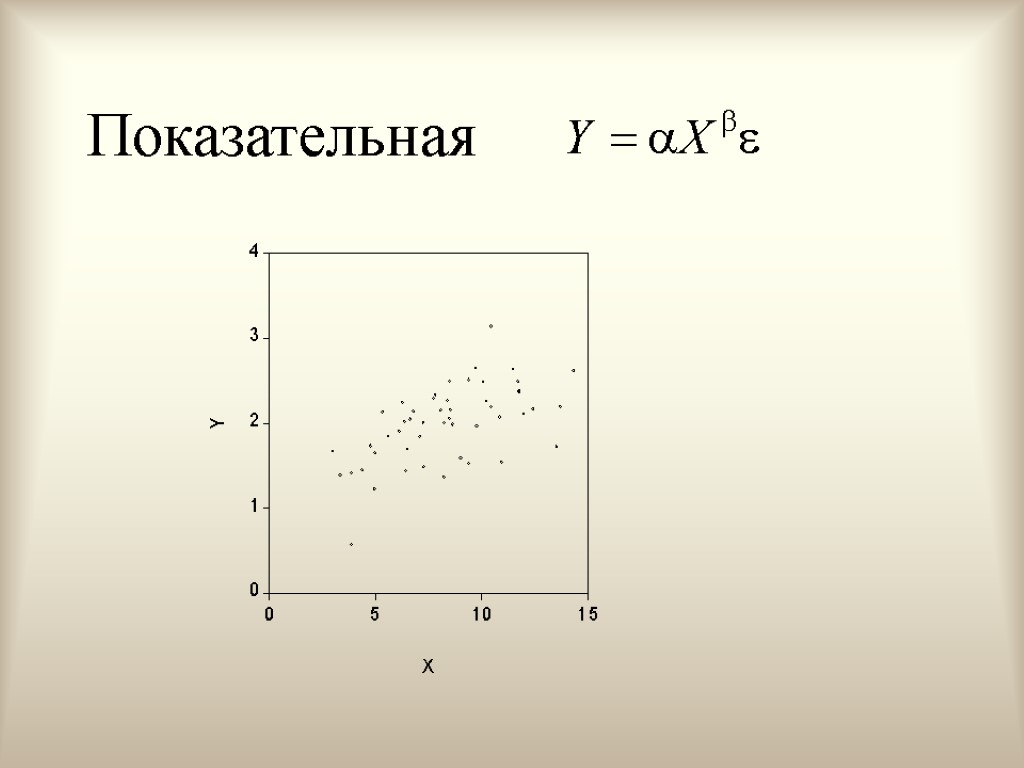
 Показательная
Показательная
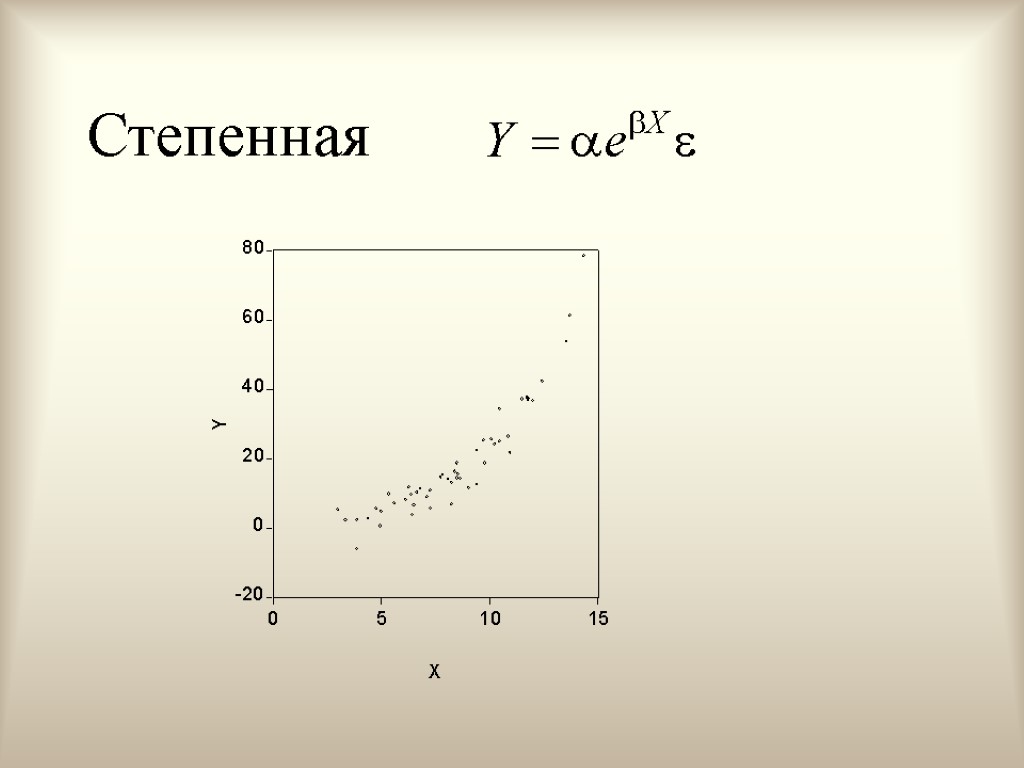
 Степенная
Степенная
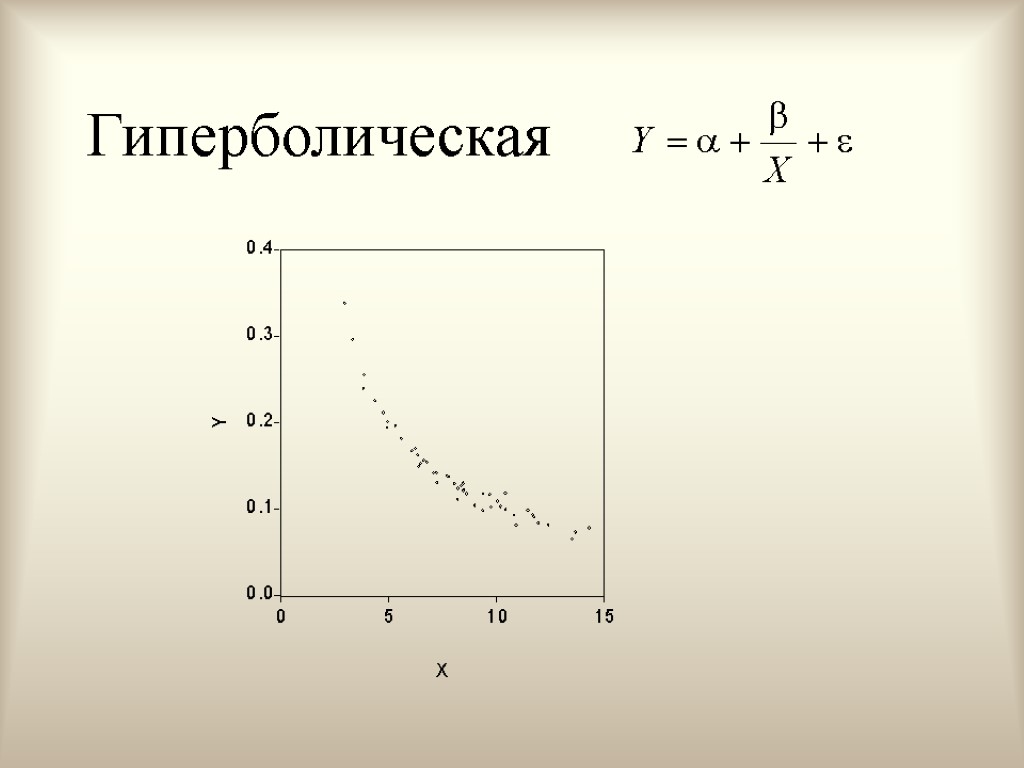
 Гиперболическая
Гиперболическая
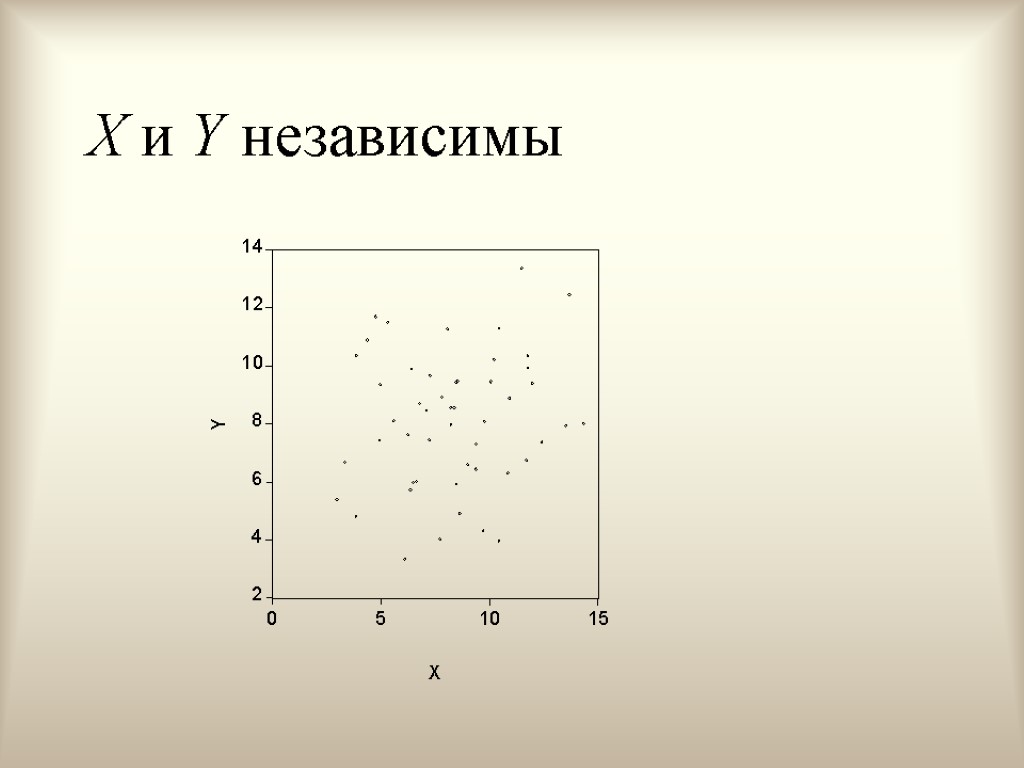
 X и Y независимы
X и Y независимы
 Парная линейная регрессионная модель Y=+X+.
Парная линейная регрессионная модель Y=+X+.
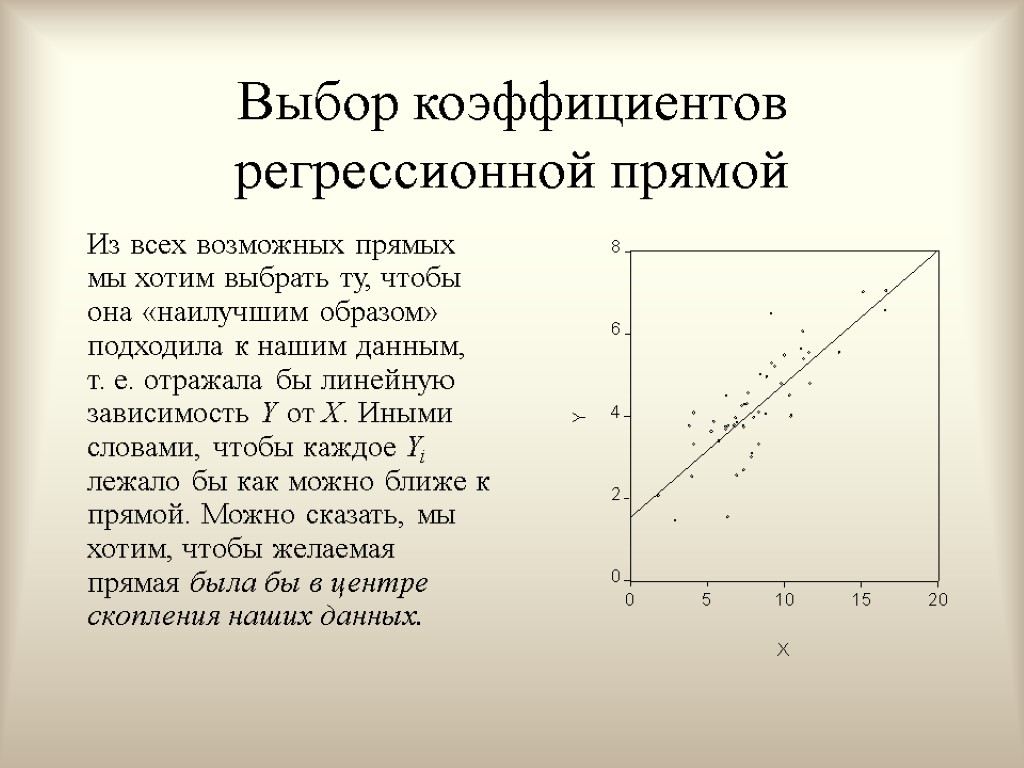
 Выбор коэффициентов регрессионной прямой Из всех возможных прямых мы хотим выбрать ту, чтобы она «наилучшим образом» подходила к нашим данным, т. е. отражала бы линейную зависимость Y от X. Иными словами, чтобы каждое Yi лежало бы как можно ближе к прямой. Можно сказать, мы хотим, чтобы желаемая прямая была бы в центре скопления наших данных.
Выбор коэффициентов регрессионной прямой Из всех возможных прямых мы хотим выбрать ту, чтобы она «наилучшим образом» подходила к нашим данным, т. е. отражала бы линейную зависимость Y от X. Иными словами, чтобы каждое Yi лежало бы как можно ближе к прямой. Можно сказать, мы хотим, чтобы желаемая прямая была бы в центре скопления наших данных.
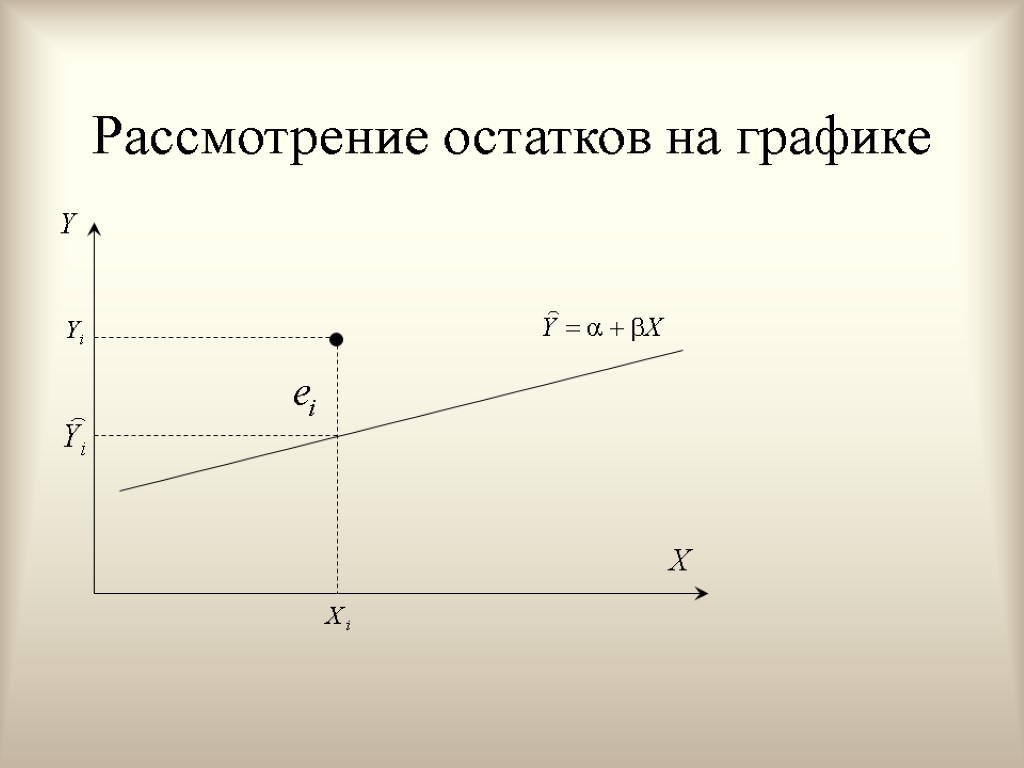
 Рассмотрение остатков на графике
Рассмотрение остатков на графике
 Интегральная мера близости
Интегральная мера близости
 Метод наименьших квадратов Среди всех возможных прямых выбираем ту, для которой сумма квадратов остатков минимальна
Метод наименьших квадратов Среди всех возможных прямых выбираем ту, для которой сумма квадратов остатков минимальна
 Минимизация или
Минимизация или
 Система нормальных уравнений
Система нормальных уравнений
 МНК-коэффициенты ПЛРМ - коэффициент наклона - свободный коэффициент
МНК-коэффициенты ПЛРМ - коэффициент наклона - свободный коэффициент
 Другие формы записи коэффициента наклона
Другие формы записи коэффициента наклона
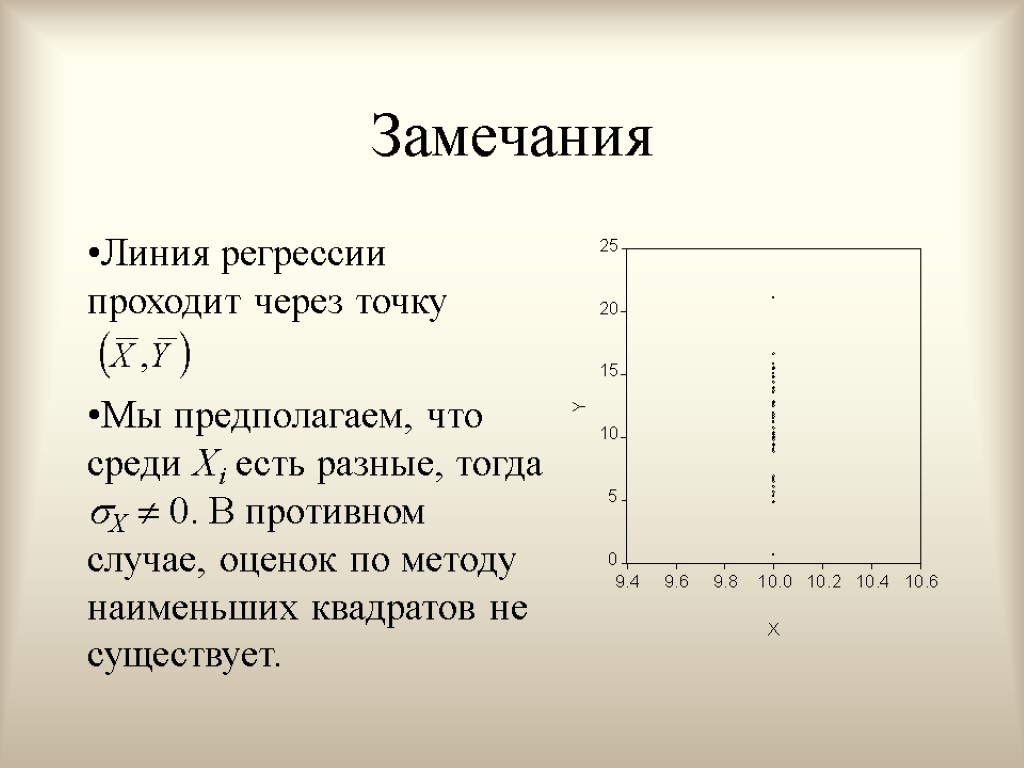
 Замечания Линия регрессии проходит через точку Мы предполагаем, что среди Xi есть разные, тогда X 0. В противном случае, оценок по методу наименьших квадратов не существует.
Замечания Линия регрессии проходит через точку Мы предполагаем, что среди Xi есть разные, тогда X 0. В противном случае, оценок по методу наименьших квадратов не существует.
 Теснота линейной корреляционной связи В качестве меры близости данных наблюдений к линии регрессии служит выборочный коэффициент парной линейной корреляции (парный линейный коэффициент корреляции):
Теснота линейной корреляционной связи В качестве меры близости данных наблюдений к линии регрессии служит выборочный коэффициент парной линейной корреляции (парный линейный коэффициент корреляции):
 Связь между коэффициентом корреляции и коэффициентом наклона Знак коэффициента наклона линии регрессии и коэффициента корреляции совпадают
Связь между коэффициентом корреляции и коэффициентом наклона Знак коэффициента наклона линии регрессии и коэффициента корреляции совпадают
 Свойства коэффициента корреляции Если - необходимое и достаточное условием того, что все наблюдаемые значения (Xi,Yi) лежат на прямой регрессии
Свойства коэффициента корреляции Если - необходимое и достаточное условием того, что все наблюдаемые значения (Xi,Yi) лежат на прямой регрессии
 Свойства коэффициента корреляции (продолжение) переменные не связаны линейной корреляционной связью. Линия регрессии проходит горизонтально. между переменными существует линейная корреляционная связь, которая тем лучше (ближе к линейной функциональной), чем ближе коэффициент корреляции по модулю к 1
Свойства коэффициента корреляции (продолжение) переменные не связаны линейной корреляционной связью. Линия регрессии проходит горизонтально. между переменными существует линейная корреляционная связь, которая тем лучше (ближе к линейной функциональной), чем ближе коэффициент корреляции по модулю к 1
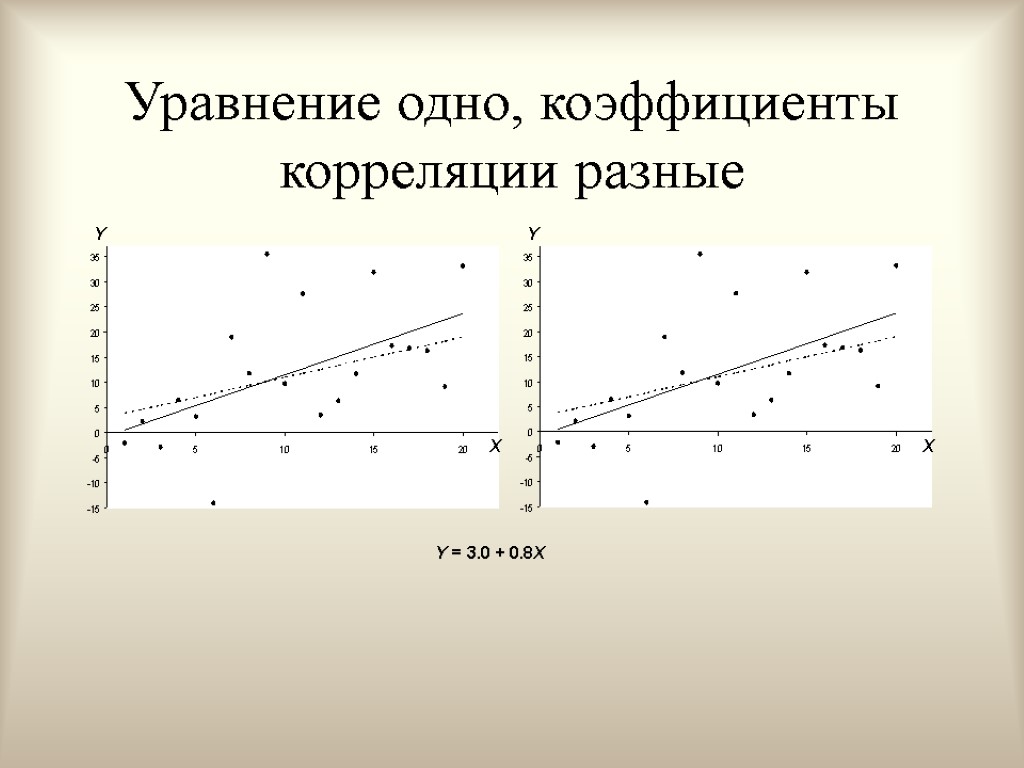
 Уравнение одно, коэффициенты корреляции разные
Уравнение одно, коэффициенты корреляции разные
 Вопросы для самопроверки Что такое функциональная зависимость между переменными. Что такое статистическая зависимость. Что такое корреляционная зависимость. Дайте определение независимых переменных. Что такое линия регрессии. Какова основная идея метода наименьших квадратов. Какие меры близости точек к линии регрессии вы знаете. Почему мы называем расчетные коэффициенты линии регрессии «статистическими оценками». Как выбрать функциональную форму линии регрессии. Форы записи МНК коэффициента наклона ергрессионной прямой. В чем заключается экономический смысл случайной составляющей регрессионного уравнения. Для чего нужен коэффициент корреляции. Как связан коэффициент корреляции и коэффициент наклона линии регрессии. Перечислите свойства коэффициента корреляции. В каком случае линии регрессии по методу наименьших квадратов не существует.
Вопросы для самопроверки Что такое функциональная зависимость между переменными. Что такое статистическая зависимость. Что такое корреляционная зависимость. Дайте определение независимых переменных. Что такое линия регрессии. Какова основная идея метода наименьших квадратов. Какие меры близости точек к линии регрессии вы знаете. Почему мы называем расчетные коэффициенты линии регрессии «статистическими оценками». Как выбрать функциональную форму линии регрессии. Форы записи МНК коэффициента наклона ергрессионной прямой. В чем заключается экономический смысл случайной составляющей регрессионного уравнения. Для чего нужен коэффициент корреляции. Как связан коэффициент корреляции и коэффициент наклона линии регрессии. Перечислите свойства коэффициента корреляции. В каком случае линии регрессии по методу наименьших квадратов не существует.
 Множественная линейная регрессионная модель
Множественная линейная регрессионная модель
 Темы лекции Множественная линейная регрессионная модель Метод наименьших квадратов оценки коэффициентов МЛРМ. Матричное выражение МНК-оценок коэффициентов МЛРМ.
Темы лекции Множественная линейная регрессионная модель Метод наименьших квадратов оценки коэффициентов МЛРМ. Матричное выражение МНК-оценок коэффициентов МЛРМ.
 Множественные регрессионные модели Независимая переменная Y характеризует состояние или поведение экономического объекта. Набор переменных X1,…,Xk, характеризуют этот экономический объект качественно или количественно. Предполагаем, что переменные X оказывают влияние на переменную Y, т. е. реализации переменной Y выступают в виде функции, значения которой определяются. правда, с некоторой погрешностью, значениями объясняющих переменных, выступающих в роли аргументов этой функции, т. е. Y = f(X1,…,Xk) + , где - случайная компонента
Множественные регрессионные модели Независимая переменная Y характеризует состояние или поведение экономического объекта. Набор переменных X1,…,Xk, характеризуют этот экономический объект качественно или количественно. Предполагаем, что переменные X оказывают влияние на переменную Y, т. е. реализации переменной Y выступают в виде функции, значения которой определяются. правда, с некоторой погрешностью, значениями объясняющих переменных, выступающих в роли аргументов этой функции, т. е. Y = f(X1,…,Xk) + , где - случайная компонента
 МЛРМ где QD объем спроса на масло, Х доход, P цена на масло, PM цена на мягкое масло. Пример
МЛРМ где QD объем спроса на масло, Х доход, P цена на масло, PM цена на мягкое масло. Пример
 Здесь нам неизвестны коэффициенты и параметры распределения . Для их оценки имеется выборка из N наблюдений над переменными Y и X1,…,Xk. Для каждого наблюдения должно выполнятся следующее равенство:
Здесь нам неизвестны коэффициенты и параметры распределения . Для их оценки имеется выборка из N наблюдений над переменными Y и X1,…,Xk. Для каждого наблюдения должно выполнятся следующее равенство:
 Матричная форма записи МЛРМ где
Матричная форма записи МЛРМ где
 Метод наименьших квадратов Среди всех возможных гиперплоскостей выбираем ту, для которой сумма квадратов остатков минимальна
Метод наименьших квадратов Среди всех возможных гиперплоскостей выбираем ту, для которой сумма квадратов остатков минимальна
 Что будем минимизировать
Что будем минимизировать
 Минимизация или
Минимизация или
 Система нормальных уравнений
Система нормальных уравнений
 Вывод формулы для нахождения коэффициентов в матричном виде
Вывод формулы для нахождения коэффициентов в матричном виде
 Вывод формулы для нахождения коэффициентов в матричном виде
Вывод формулы для нахождения коэффициентов в матричном виде
 Итог МНК оценки коэффициентов МЛРМ
Итог МНК оценки коэффициентов МЛРМ
 Полная мультиколлинеарность Коэффициенты по методу наименьших квадратов существуют не всегда, а только в том случае, когда определитель матрицы (X’X) отличен от нуля. Определитель будет равен нулю в случае, если столбцы матрицы X линейно зависимы. Такое может произойти, если между независимыми переменными существует точное линейное соотношение.
Полная мультиколлинеарность Коэффициенты по методу наименьших квадратов существуют не всегда, а только в том случае, когда определитель матрицы (X’X) отличен от нуля. Определитель будет равен нулю в случае, если столбцы матрицы X линейно зависимы. Такое может произойти, если между независимыми переменными существует точное линейное соотношение.
 Пример где Y - средняя оценка на экзамене состоящую из трех объясняющих переменных: I доход родителей, D среднее число часов, затраченных на обучение в день, W среднее число часов, затраченных на обучение в неделю. Очевидно, что W=7D.
Пример где Y - средняя оценка на экзамене состоящую из трех объясняющих переменных: I доход родителей, D среднее число часов, затраченных на обучение в день, W среднее число часов, затраченных на обучение в неделю. Очевидно, что W=7D.
 Устранение полной мультиколлинеарности Случай полной мультиколлинеарности отследить легко, поскольку в этом случае невозможно построить оценки по методу наименьших квадратов. Если в модели присутствует полная мультиколлинеарность, следует удалить из регрессионного уравнения одну из переменных, которые входят в линейное соотношение.
Устранение полной мультиколлинеарности Случай полной мультиколлинеарности отследить легко, поскольку в этом случае невозможно построить оценки по методу наименьших квадратов. Если в модели присутствует полная мультиколлинеарность, следует удалить из регрессионного уравнения одну из переменных, которые входят в линейное соотношение.
 Вопросы для самопроверки Система нормальных уравнений для нахождения коэффициентов по МНК. В каком случае линии регрессии по методу наименьших квадратов не существует Приведите примет модели, в которой присутствует полная мультиколлинеарность. Укажите размерности матриц, участвующих в формуле МНК-коэффициентов. .Как устранить проблему полной мультиколлинеарности. Выведите систему нормальных уравнений. Выведите матричную формулу МНК коэффициентов. Приведите пример ситуации, когда линейной зависимости между объясняющими переменными нет, а коэффииценты МЛРМ не существуют. Как влияют выбросы на результаты оценивания. Как исследовать устойчивость результатов оценивания.
Вопросы для самопроверки Система нормальных уравнений для нахождения коэффициентов по МНК. В каком случае линии регрессии по методу наименьших квадратов не существует Приведите примет модели, в которой присутствует полная мультиколлинеарность. Укажите размерности матриц, участвующих в формуле МНК-коэффициентов. .Как устранить проблему полной мультиколлинеарности. Выведите систему нормальных уравнений. Выведите матричную формулу МНК коэффициентов. Приведите пример ситуации, когда линейной зависимости между объясняющими переменными нет, а коэффииценты МЛРМ не существуют. Как влияют выбросы на результаты оценивания. Как исследовать устойчивость результатов оценивания.
 Тема 4. Оценка качества подгонки линии регрессии к имеющимся данным
Тема 4. Оценка качества подгонки линии регрессии к имеющимся данным
 Темы лекции. Коэффициент детерминации. Свойства коэффициента детерминации. Скорректированный коэффициент детерминации. Свойства скорректированного коэффициента детерминации.
Темы лекции. Коэффициент детерминации. Свойства коэффициента детерминации. Скорректированный коэффициент детерминации. Свойства скорректированного коэффициента детерминации.
 Насколько хорошо нам удалось объяснить изменение переменной Y нашей моделью. Разложим вариацию Y на две части. Насколько наше уравнение объясняет вариацию Y и какова часть Y, которую мы не можем объяснить нашим уравнением.
Насколько хорошо нам удалось объяснить изменение переменной Y нашей моделью. Разложим вариацию Y на две части. Насколько наше уравнение объясняет вариацию Y и какова часть Y, которую мы не можем объяснить нашим уравнением.
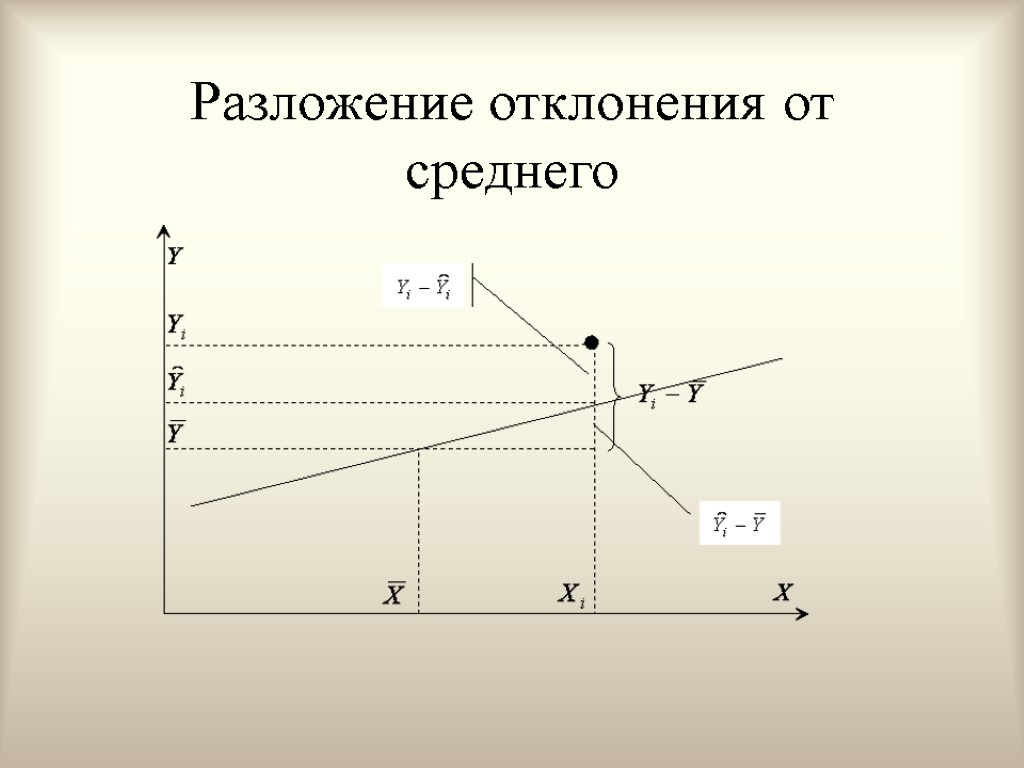
 Разложение отклонения от среднего
Разложение отклонения от среднего
 Общая вариация переменной Y величина, являющаяся мерой вариации переменной Y вокруг ее среднего значения
Общая вариация переменной Y величина, являющаяся мерой вариации переменной Y вокруг ее среднего значения
 Разложение общей вариации переменной Y В этой сумме II = 0, если в уравнении есть свободный коэффициент I II III
Разложение общей вариации переменной Y В этой сумме II = 0, если в уравнении есть свободный коэффициент I II III
 TSS – total sum of squares – вся дисперсия или вариация Y, характеризует степень случайного разброса значений функции регрессии около среднего значения Y ESS – error sum of squares – есть сумма квадратов остатков регрессии, та величина, которую мы минимизируем при построении прямой, часть дисперсии, которая нашим уравнением не объясняется RSS – regression sum of squares – объясненная часть общей вариации
TSS – total sum of squares – вся дисперсия или вариация Y, характеризует степень случайного разброса значений функции регрессии около среднего значения Y ESS – error sum of squares – есть сумма квадратов остатков регрессии, та величина, которую мы минимизируем при построении прямой, часть дисперсии, которая нашим уравнением не объясняется RSS – regression sum of squares – объясненная часть общей вариации
 Коэффициент детерминации Коэффициентом детерминации или долей объясненной нашим уравнением дисперсии называется величина
Коэффициент детерминации Коэффициентом детерминации или долей объясненной нашим уравнением дисперсии называется величина
 Свойства коэффициента детерминации в силу определения;
Свойства коэффициента детерминации в силу определения;
 в это м случае RSS = 0, т. е. наша регрессия ничего не объясняет, ничего не дает по сравнению с тривиальным прогнозом наши данные позволяют сделать вывод о независимости Y и X, изменение в переменной X никак не влияет на изменение среднего значения переменной Y (есть примеры, когда зависимость между переменными есть, а коэффициент детерминации равен нулю);
в это м случае RSS = 0, т. е. наша регрессия ничего не объясняет, ничего не дает по сравнению с тривиальным прогнозом наши данные позволяют сделать вывод о независимости Y и X, изменение в переменной X никак не влияет на изменение среднего значения переменной Y (есть примеры, когда зависимость между переменными есть, а коэффициент детерминации равен нулю);
 в этом случае чем ближе R2 к 1, тем лучше качество подгонки кривой к нашим данным, тем точнее аппроксимирует Y
в этом случае чем ближе R2 к 1, тем лучше качество подгонки кривой к нашим данным, тем точнее аппроксимирует Y
 в этом случае все точки (Xi, Yi) лежат на одной прямой (ESS = 0). Тогда на основании наших данных можно сделать вывод о наличии функциональной, а именно, линейной, зависимости между переменными Y и X. Изменение переменной Y полностью объясняется изменением переменной X
в этом случае все точки (Xi, Yi) лежат на одной прямой (ESS = 0). Тогда на основании наших данных можно сделать вывод о наличии функциональной, а именно, линейной, зависимости между переменными Y и X. Изменение переменной Y полностью объясняется изменением переменной X
 Недостаток коэффициента детерминации R2, вообще говоря, возрастает при добавлении еще одного регрессора, поэтому для выбора между несколькими регрессионными уравнениями не следует полагаться только на R2
Недостаток коэффициента детерминации R2, вообще говоря, возрастает при добавлении еще одного регрессора, поэтому для выбора между несколькими регрессионными уравнениями не следует полагаться только на R2
 Скорректированный коэффициент детерминации Попыткой устранить эффект, связанный с ростом R2 при увеличении числа регрессоров, является коррекция R2 на число регрессоров - наложение "штрафа" за увеличение числа независимых переменных.
Скорректированный коэффициент детерминации Попыткой устранить эффект, связанный с ростом R2 при увеличении числа регрессоров, является коррекция R2 на число регрессоров - наложение "штрафа" за увеличение числа независимых переменных.
 Скорректированный коэффициент детерминации
Скорректированный коэффициент детерминации
 Свойства скорректированного коэффициента детерминации , но может быть и < 0
Свойства скорректированного коэффициента детерминации , но может быть и < 0
 Упражнение Показать, что статистика увеличится при добавлении новой переменной тогда и только тогда, когда t-статистика коэффициента при этой переменной по модулю больше 1. Следовательно, если в результате регрессии с новой переменной увеличился, это еще не означает, что коэффициент при этой переменной значимо отличается от нуля, поэтому мы не можем сказать, что спецификация модели улучшилась
Упражнение Показать, что статистика увеличится при добавлении новой переменной тогда и только тогда, когда t-статистика коэффициента при этой переменной по модулю больше 1. Следовательно, если в результате регрессии с новой переменной увеличился, это еще не означает, что коэффициент при этой переменной значимо отличается от нуля, поэтому мы не можем сказать, что спецификация модели улучшилась
 Вопросы для самопроверки Для чего нужен коэффициент детерминации. Основная идея построения характеристики качества подгонки линии регрессии к имеющимся данным. Как связаны между собой коэффициент детерминации и коэффициент корреляции в парной модели. В каком случае коэффициент детерминации имеет смысл. Докажите, что второе слагаемое в разложении общей вариации равно нулю. Какие вы знаете свойства коэффициента детерминации В каких случаях нельзя использовать коэффициент детерминации для сравнения моделей. Что такое скорректированный коэффициент детерминации. Всегда ли скорректированный коэффициент детерминации увеличивается при добавлении новых переменных. Перечислите свойства скорректированного коэффициента детерминации
Вопросы для самопроверки Для чего нужен коэффициент детерминации. Основная идея построения характеристики качества подгонки линии регрессии к имеющимся данным. Как связаны между собой коэффициент детерминации и коэффициент корреляции в парной модели. В каком случае коэффициент детерминации имеет смысл. Докажите, что второе слагаемое в разложении общей вариации равно нулю. Какие вы знаете свойства коэффициента детерминации В каких случаях нельзя использовать коэффициент детерминации для сравнения моделей. Что такое скорректированный коэффициент детерминации. Всегда ли скорректированный коэффициент детерминации увеличивается при добавлении новых переменных. Перечислите свойства скорректированного коэффициента детерминации
 Тема 4. Нелинейные модели
Тема 4. Нелинейные модели
 Темы лекции Нелинейная регрессия Преобразования переменных Экономическая интерпретация регрессионной модели
Темы лекции Нелинейная регрессия Преобразования переменных Экономическая интерпретация регрессионной модели
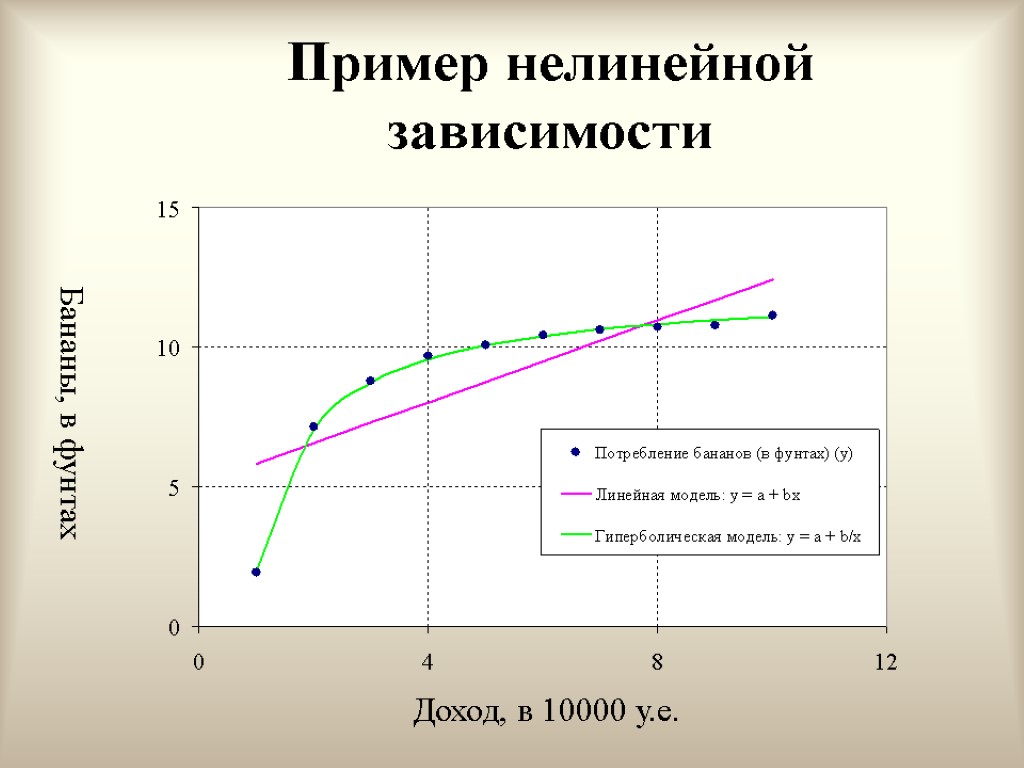
 Пример нелинейной зависимости Бананы, в фунтах Доход, в 10000 у.е.
Пример нелинейной зависимости Бананы, в фунтах Доход, в 10000 у.е.
 Направления анализа и развития парной линейной регрессии Ключевые точки (начало координат) Кривая или прямая Форма криволинейной зависимости Вспомогательные экономические показатели (скорость и темп роста, эластичность) Уточнение формы (экстремумы, пределы) Сравнение функциональных форм
Направления анализа и развития парной линейной регрессии Ключевые точки (начало координат) Кривая или прямая Форма криволинейной зависимости Вспомогательные экономические показатели (скорость и темп роста, эластичность) Уточнение формы (экстремумы, пределы) Сравнение функциональных форм
 Этапы построения модели 1. Выбор теоретических предпосылок 2. Формализация предпосылок 3. Построение математической модели 4. Анализ построенной модели
Этапы построения модели 1. Выбор теоретических предпосылок 2. Формализация предпосылок 3. Построение математической модели 4. Анализ построенной модели
 Производственная функция Кобба-Дугласа Многие экономические процессы не являются линейными по сути. Их моделирование линейными уравнениями не даст положительного результата. Пример. Производственная функция Кобба – Дугласа Y – объем выпуска; K, L – затраты капитала и труда; , – параметры модели.
Производственная функция Кобба-Дугласа Многие экономические процессы не являются линейными по сути. Их моделирование линейными уравнениями не даст положительного результата. Пример. Производственная функция Кобба – Дугласа Y – объем выпуска; K, L – затраты капитала и труда; , – параметры модели.
 Анализ экономического роста Анализ теоретических предпосылок: прирост пропорционален накопленному потенциалу Формализация предпосылок: Интерпретация и анализ: коэффициент регрессии годовой темп роста, возможно сопоставление с реальными данными
Анализ экономического роста Анализ теоретических предпосылок: прирост пропорционален накопленному потенциалу Формализация предпосылок: Интерпретация и анализ: коэффициент регрессии годовой темп роста, возможно сопоставление с реальными данными
 Классы нелинейных регрессий Различают два класса нелинейных регрессий: 1. Регрессии, нелинейные относительно переменных, но линейные по оцениваемым параметрам. 2. Регрессии, нелинейные по оцениваемых параметрам. Регрессии, нелинейные относительно объясняющих переменных, всегда сводятся к линейным моделям.
Классы нелинейных регрессий Различают два класса нелинейных регрессий: 1. Регрессии, нелинейные относительно переменных, но линейные по оцениваемым параметрам. 2. Регрессии, нелинейные по оцениваемых параметрам. Регрессии, нелинейные относительно объясняющих переменных, всегда сводятся к линейным моделям.
 Альтернативные функциональные формы: правила выбора Правила выбора формы зависимости: 1. Исходить из экономической теории. 2. Оценивать формальное качество модели. 3. Дополнительно проверять по нескольким содержательным критериям. 4. Ответить на вопросы, возникающие при анализе модели: каковы признаки качественной модели; какие ошибки спецификации встречаются и каковы их последствия; как обнаружить ошибку спецификации; каким образом можно исправить ошибку спецификации и перейти к более качественной модели.
Альтернативные функциональные формы: правила выбора Правила выбора формы зависимости: 1. Исходить из экономической теории. 2. Оценивать формальное качество модели. 3. Дополнительно проверять по нескольким содержательным критериям. 4. Ответить на вопросы, возникающие при анализе модели: каковы признаки качественной модели; какие ошибки спецификации встречаются и каковы их последствия; как обнаружить ошибку спецификации; каким образом можно исправить ошибку спецификации и перейти к более качественной модели.
 Линейная форма Интерпретация коэффициента регрессии предельный эффект независимого фактора
Линейная форма Интерпретация коэффициента регрессии предельный эффект независимого фактора
 Линейная форма Для полученных оценок a, b уравнения регрессии:
Линейная форма Для полученных оценок a, b уравнения регрессии:
 Линейная форма Коэффициент регрессии b показывает прирост зависимой переменной при изменении объясняющей переменной на единицу. Коэффициент регрессии b – угловой коэффициент линии регрессии Коэффициент регрессии a – среднее значение зависимой переменной при нулевом значении объясняющей переменной
Линейная форма Коэффициент регрессии b показывает прирост зависимой переменной при изменении объясняющей переменной на единицу. Коэффициент регрессии b – угловой коэффициент линии регрессии Коэффициент регрессии a – среднее значение зависимой переменной при нулевом значении объясняющей переменной
 Линейная форма от времени Интерпретация коэффициента регрессии от времени ежегодный (ежемесячный и т.д.) прирост зависимой переменной
Линейная форма от времени Интерпретация коэффициента регрессии от времени ежегодный (ежемесячный и т.д.) прирост зависимой переменной
 Моделирование эластичности Независимо от вида математической связи между Y и X эластичность равна: Эластичность y по x рассчитывается как относительное изменение y на единицу относительного изменения x.
Моделирование эластичности Независимо от вида математической связи между Y и X эластичность равна: Эластичность y по x рассчитывается как относительное изменение y на единицу относительного изменения x.
 Пример расчета эластичности Рассмотрим кривую Энгеля: где Y – спрос на товар, X – доход. Имеем: Эластичность = Например для модели эластичность спроса по доходу равна 0,3. Иными словами, изменение дохода (X) на 1% вызывает изменение спроса (Y) на 0,3%
Пример расчета эластичности Рассмотрим кривую Энгеля: где Y – спрос на товар, X – доход. Имеем: Эластичность = Например для модели эластичность спроса по доходу равна 0,3. Иными словами, изменение дохода (X) на 1% вызывает изменение спроса (Y) на 0,3%
 Эластичность – переменная величина Например, для линейной модели Эластичность не всегда бывает постоянной для различных значений X и Y
Эластичность – переменная величина Например, для линейной модели Эластичность не всегда бывает постоянной для различных значений X и Y
 Средний коэффициент эластичности Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат Y от своей средней величины при изменении фактора X на 1% от своего среднего значения
Средний коэффициент эластичности Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат Y от своей средней величины при изменении фактора X на 1% от своего среднего значения
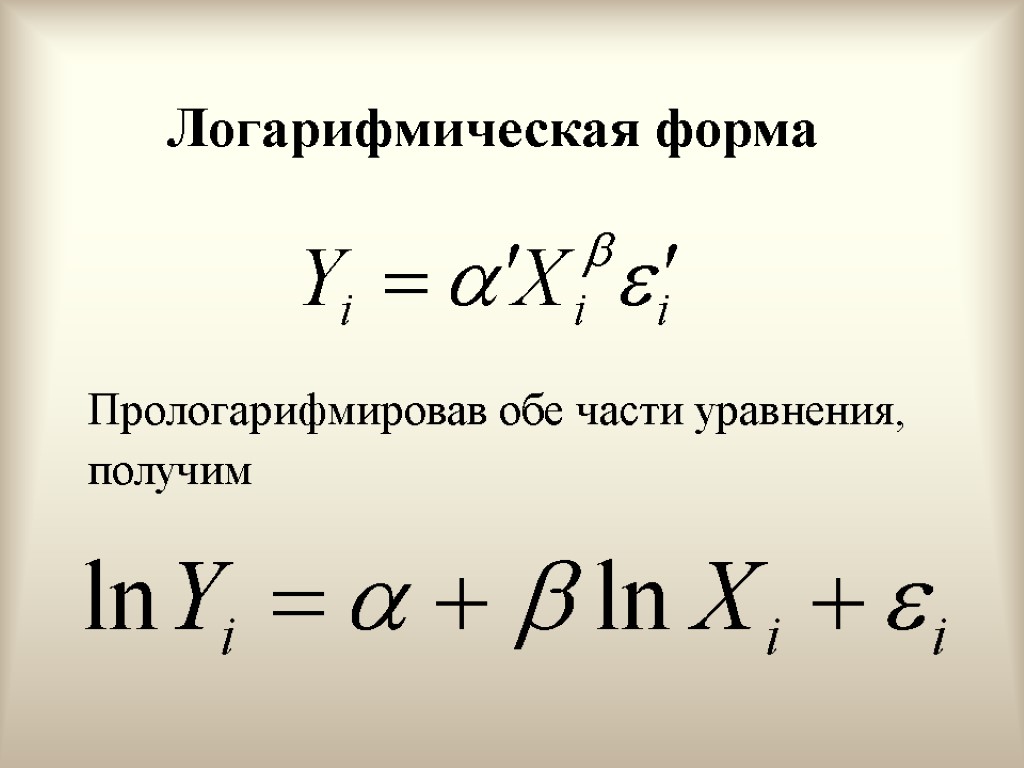 Логарифмическая форма Прологарифмировав обе части уравнения, получим
Логарифмическая форма Прологарифмировав обе части уравнения, получим
 Логарифмическая форма Интерпретация коэффициента регрессии – эластичность зависимой переменной по объясняющей переменной Коэффициент при объясняющей переменной показывает, на сколько процентов возрастает Y при возрастании X на 1%. Логарифмическую форму следует использовать там, где есть основание предполагать постоянство эластичности
Логарифмическая форма Интерпретация коэффициента регрессии – эластичность зависимой переменной по объясняющей переменной Коэффициент при объясняющей переменной показывает, на сколько процентов возрастает Y при возрастании X на 1%. Логарифмическую форму следует использовать там, где есть основание предполагать постоянство эластичности
 Логарифмическая форма Вычисление наклона (скорости роста) Наклон постоянно меняется с изменением номера наблюдения
Логарифмическая форма Вычисление наклона (скорости роста) Наклон постоянно меняется с изменением номера наблюдения
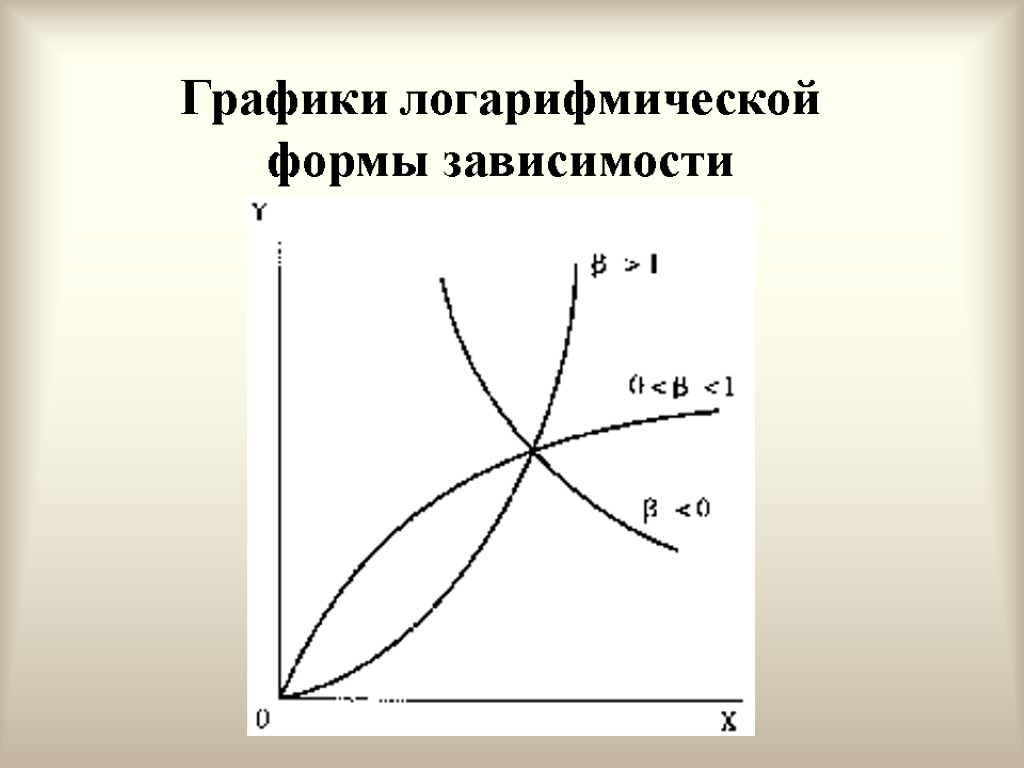
 Графики логарифмической формы зависимости
Графики логарифмической формы зависимости
 Полулогарифмические формы 1. Линейно-логарифмическая форма (логарифм при объясняющей переменной) 2. Логарифмически-линейная форма (логарифм при зависимой переменной)
Полулогарифмические формы 1. Линейно-логарифмическая форма (логарифм при объясняющей переменной) 2. Логарифмически-линейная форма (логарифм при зависимой переменной)
 Линейно-логарифмическая форма Интерпретация коэффициента регрессии : Коэффициент при объясняющей переменной показывает на сколько единиц возрастает Y при возрастании X на 1% При интерпретации коэффициент следует делить на 100 Если X увеличится на 1%, то прирост Y составит /100 единиц (в которых измеряется Y)
Линейно-логарифмическая форма Интерпретация коэффициента регрессии : Коэффициент при объясняющей переменной показывает на сколько единиц возрастает Y при возрастании X на 1% При интерпретации коэффициент следует делить на 100 Если X увеличится на 1%, то прирост Y составит /100 единиц (в которых измеряется Y)
 Линейно-логарифмическая форма Эластичность убывает с ростом Y: Это указывает на класс зависимостей, где следует применять линейно-логарифмическую форму регрессии Логарифм при X снижает влияние роста X (степень влияния X снижается с ростом X). Моделирование эффектов насыщения на уровне скорости роста: «возрастание с убывающей скоростью»
Линейно-логарифмическая форма Эластичность убывает с ростом Y: Это указывает на класс зависимостей, где следует применять линейно-логарифмическую форму регрессии Логарифм при X снижает влияние роста X (степень влияния X снижается с ростом X). Моделирование эффектов насыщения на уровне скорости роста: «возрастание с убывающей скоростью»
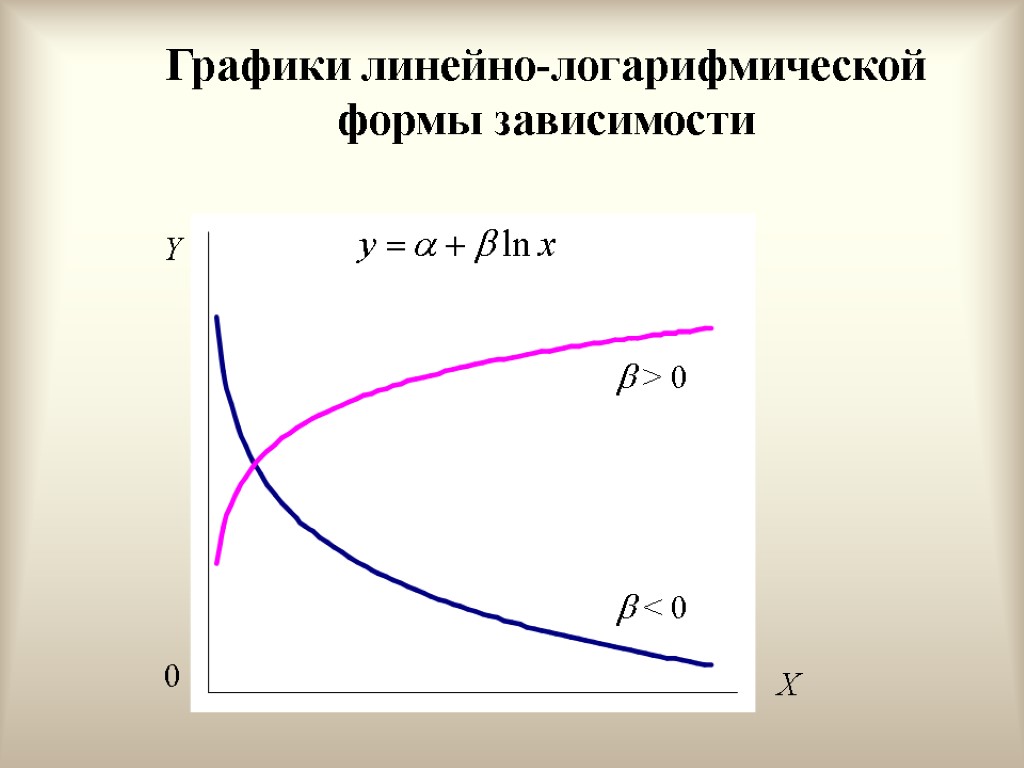
 Графики линейно-логарифмической формы зависимости 0 X Y > 0 < 0
Графики линейно-логарифмической формы зависимости 0 X Y > 0 < 0
 Логарифмически-линейная форма Интерпретация коэффициента регрессии : Коэффициент при объясняющей переменной показывает на сколько процентов возрастает Y при возрастании X на одну единицу При интерпретации коэффициент следует умножать на 100
Логарифмически-линейная форма Интерпретация коэффициента регрессии : Коэффициент при объясняющей переменной показывает на сколько процентов возрастает Y при возрастании X на одну единицу При интерпретации коэффициент следует умножать на 100
 Логарифмически-линейная форма Эластичность растет с ростом Y: Это указывает на класс зависимостей, где следует применять линейно-логарифмическую форму регрессии Моделирование эффектов насыщения на уровне скорости роста: «возрастание с возрастающей скоростью» Примеры: кривые Энгеля для товаров роскоши, моделирование оплаты труда (процентная надбавка за стаж и опыт)
Логарифмически-линейная форма Эластичность растет с ростом Y: Это указывает на класс зависимостей, где следует применять линейно-логарифмическую форму регрессии Моделирование эффектов насыщения на уровне скорости роста: «возрастание с возрастающей скоростью» Примеры: кривые Энгеля для товаров роскоши, моделирование оплаты труда (процентная надбавка за стаж и опыт)
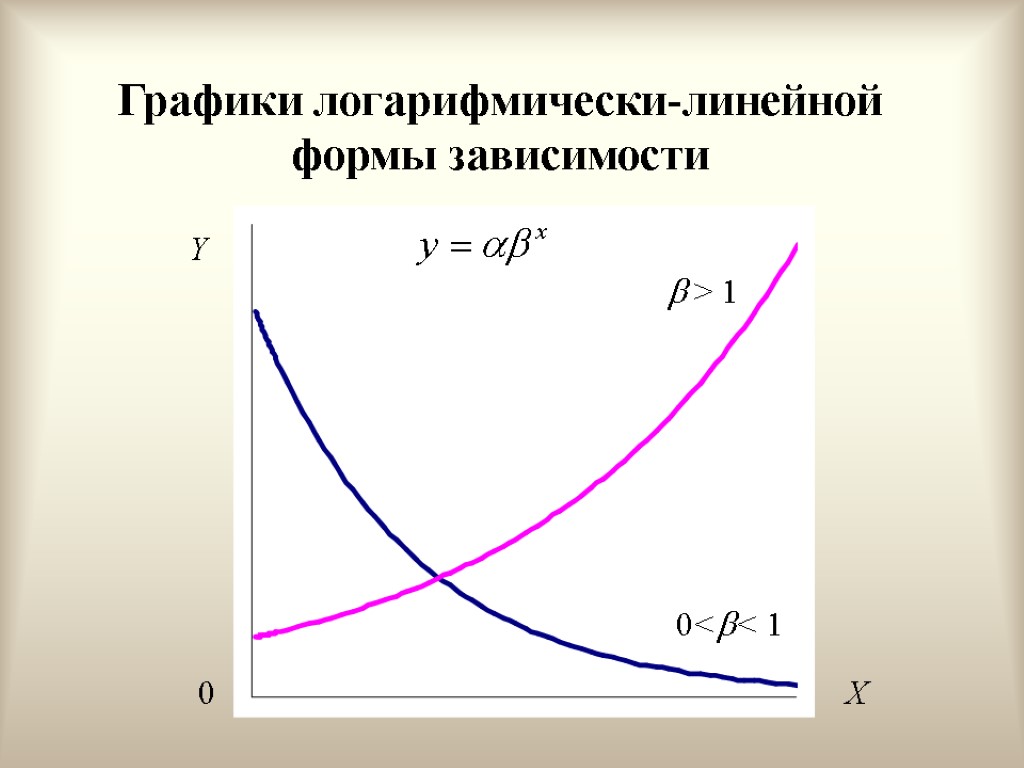
 Графики логарифмически-линейной формы зависимости Y > 1 0<< 1 X 0
Графики логарифмически-линейной формы зависимости Y > 1 0<< 1 X 0
 Логарифмически-линейная форма от времени Вид уравнения: Интерпретация: Коэффициент при переменной времени выражает темп прироста. Он показывает на сколько процентов (если умножить его на 100) возрастает Y ежегодно Эту функциональную форму удобно использовать для моделирования процессов экономического роста
Логарифмически-линейная форма от времени Вид уравнения: Интерпретация: Коэффициент при переменной времени выражает темп прироста. Он показывает на сколько процентов (если умножить его на 100) возрастает Y ежегодно Эту функциональную форму удобно использовать для моделирования процессов экономического роста
 Обратные зависимости Вычисление эластичности С ростом X зависимая переменная приближается к некоторому числу (моделирование эффекта насыщения) Пример: Моделирование потребления товаров первой необходимости (быстрое достижение насыщения)
Обратные зависимости Вычисление эластичности С ростом X зависимая переменная приближается к некоторому числу (моделирование эффекта насыщения) Пример: Моделирование потребления товаров первой необходимости (быстрое достижение насыщения)
 Сводка результатов для альтернативных функциональных форм в парной регрессии
Сводка результатов для альтернативных функциональных форм в парной регрессии
 Преобразование случайного отклонения Пример. Логарифмирование нелинейной модели с аддитивным случайным членом не приводит к линеаризации соотношения относительно параметров. МНК применяется к преобразованным (линеаризованным) уравнениям. Поэтому необходимо особое внимание уделять рассмотрению свойств случайных отклонений – выполнимости предпосылок теоремы Гаусса-Маркова.
Преобразование случайного отклонения Пример. Логарифмирование нелинейной модели с аддитивным случайным членом не приводит к линеаризации соотношения относительно параметров. МНК применяется к преобразованным (линеаризованным) уравнениям. Поэтому необходимо особое внимание уделять рассмотрению свойств случайных отклонений – выполнимости предпосылок теоремы Гаусса-Маркова.
 Признаки качественной модели 1. Простота модели (из примерно одинаково отражающих реальность моделей, выбирается та, которая содержит меньше объясняющих переменных. 2. Единственность (для любых данных коэффициенты модели должны вычисляться однозначно). 3. Максимальное соответствие (модель тем лучше, чем больше скорректированный коэффициент детерминации). 4. Согласованность с теорией (уравнение регрессии должно соответствовать теоретическим предпосылкам). 5. Прогнозные качества (прогнозы, полученные на основе модели, должны подтверждаться реальностью).
Признаки качественной модели 1. Простота модели (из примерно одинаково отражающих реальность моделей, выбирается та, которая содержит меньше объясняющих переменных. 2. Единственность (для любых данных коэффициенты модели должны вычисляться однозначно). 3. Максимальное соответствие (модель тем лучше, чем больше скорректированный коэффициент детерминации). 4. Согласованность с теорией (уравнение регрессии должно соответствовать теоретическим предпосылкам). 5. Прогнозные качества (прогнозы, полученные на основе модели, должны подтверждаться реальностью).
 Сравнение различных моделей 1. Содержательный анализ 2. Формальный анализ: Метод Зарембки Преобразование Бокса-Кокса
Сравнение различных моделей 1. Содержательный анализ 2. Формальный анализ: Метод Зарембки Преобразование Бокса-Кокса
 Метод Зарембки Применим для выбора из двух форм (несравнимых непосредственно), в одной из которых зависимая переменная входит с логарифмом, а в другой – нет Метод позволяет сравнить линейную и логарифмическую регрессии и оценить значимость наблюдаемых различий
Метод Зарембки Применим для выбора из двух форм (несравнимых непосредственно), в одной из которых зависимая переменная входит с логарифмом, а в другой – нет Метод позволяет сравнить линейную и логарифмическую регрессии и оценить значимость наблюдаемых различий
 Сравнение различных моделей парной регрессии методом Зарембки 1. Вычисляем среднее геометрическое значений зависимой переменной и все ее значения делим на это среднее: 2. Рассчитываются линейная и логарифмическая регрессии, и сравниваются значения их сумм квадратов остатков (ESS)
Сравнение различных моделей парной регрессии методом Зарембки 1. Вычисляем среднее геометрическое значений зависимой переменной и все ее значения делим на это среднее: 2. Рассчитываются линейная и логарифмическая регрессии, и сравниваются значения их сумм квадратов остатков (ESS)
 Сравнение различных моделей парной регрессии методом Зарембки 3. Вычисляем 2-статистику для оценки значимости различий 4. Сравниваем с критическим значением 2-распределения . Различия значимы на уровне значимости , если
Сравнение различных моделей парной регрессии методом Зарембки 3. Вычисляем 2-статистику для оценки значимости различий 4. Сравниваем с критическим значением 2-распределения . Различия значимы на уровне значимости , если
 Метод Бокса-Кокса Идея метода. Переменная : при =1 превращается в линейную функцию при 0 переходит в логарифм Плавно изменяя , можно постепенно перейти от линейной регрессии к логарифмической, все время сравнивая качество
Метод Бокса-Кокса Идея метода. Переменная : при =1 превращается в линейную функцию при 0 переходит в логарифм Плавно изменяя , можно постепенно перейти от линейной регрессии к логарифмической, все время сравнивая качество
 Сравнение различных моделей парной регрессии методом Бокса-Кокса 1. Преобразуют зависимую переменную по методу Зарембки: 2. Рассчитывают новые переменные (преобразование Бокса-Кокса) при значениях от 1 до 0:
Сравнение различных моделей парной регрессии методом Бокса-Кокса 1. Преобразуют зависимую переменную по методу Зарембки: 2. Рассчитывают новые переменные (преобразование Бокса-Кокса) при значениях от 1 до 0:
 Сравнение различных моделей парной регрессии методом Бокса-Кокса 3. Рассчитывают уравнения регрессии для новых переменных при значениях от 1 до 0: 4. Определяют минимальное значение суммы квадратов остатков (SSR). 5. Выбирают одну из крайних регрессий, к которой ближе точка минимума.
Сравнение различных моделей парной регрессии методом Бокса-Кокса 3. Рассчитывают уравнения регрессии для новых переменных при значениях от 1 до 0: 4. Определяют минимальное значение суммы квадратов остатков (SSR). 5. Выбирают одну из крайних регрессий, к которой ближе точка минимума.
 Вопросы для самопроверки Какие вы знаете виды нелинейных моделей. Какие вы знаете нелинейные методы оценивания. Как определять эластичность. Что такое предельные эффекты переменных. Основные способы линеаризации моделей. Какие вы знаете типы производственных функций. Как выбрать между линейной и логарифмической моделями. Экономический смысл коэффициентов линейной модели. Экономический смысл коэффициентов логарифмической модели Экономический смысл коэффициентов полулогарифмической модели.
Вопросы для самопроверки Какие вы знаете виды нелинейных моделей. Какие вы знаете нелинейные методы оценивания. Как определять эластичность. Что такое предельные эффекты переменных. Основные способы линеаризации моделей. Какие вы знаете типы производственных функций. Как выбрать между линейной и логарифмической моделями. Экономический смысл коэффициентов линейной модели. Экономический смысл коэффициентов логарифмической модели Экономический смысл коэффициентов полулогарифмической модели.
 Тема 6. Статистические свойства МНК-оценок
Тема 6. Статистические свойства МНК-оценок
 Темы лекции Условия Гаусса-Маркова Статистические свойства МНК-оценок. Распределение МНК-коэффициентов Оценка параметров распределения МНК-коэффициентов
Темы лекции Условия Гаусса-Маркова Статистические свойства МНК-оценок. Распределение МНК-коэффициентов Оценка параметров распределения МНК-коэффициентов
 Для того чтобы оценки, полученные по МНК, давали «наилучшие» результаты, мы потребуем от остаточного члена или ошибки и от X выполнения следующих условий (предположения относительно того, как генерируются наблюдения):
Для того чтобы оценки, полученные по МНК, давали «наилучшие» результаты, мы потребуем от остаточного члена или ошибки и от X выполнения следующих условий (предположения относительно того, как генерируются наблюдения):
 Условия Гаусса-Маркова - спецификация модели X1,…,Xk – детерминированные вектора, линейно независимые в Rn, т. е. матрица X имеет максимальный ранг k (в повторяющихся наблюдениях единственным источником случайных возмущений вектора Y являются случайные возмущения вектора ) , дисперсия ошибки не зависит от номера наблюдения; при i k, т. е. некоррелированность ошибок разных наблюдений; , т. е. . i –нормально распределенная случайная величина со средним 0 и дисперсией .
Условия Гаусса-Маркова - спецификация модели X1,…,Xk – детерминированные вектора, линейно независимые в Rn, т. е. матрица X имеет максимальный ранг k (в повторяющихся наблюдениях единственным источником случайных возмущений вектора Y являются случайные возмущения вектора ) , дисперсия ошибки не зависит от номера наблюдения; при i k, т. е. некоррелированность ошибок разных наблюдений; , т. е. . i –нормально распределенная случайная величина со средним 0 и дисперсией .
 Условия Гаусса-Маркова в матричной форме - матрица ковариаций вектора ошибок. Матрица предполагается положительно определенной
Условия Гаусса-Маркова в матричной форме - матрица ковариаций вектора ошибок. Матрица предполагается положительно определенной
 Интерпретация условий (условие 1) Спецификация модели отражает наше представление о механизме зависимости Y и X и выбор объясняющих переменных X.
Интерпретация условий (условие 1) Спецификация модели отражает наше представление о механизме зависимости Y и X и выбор объясняющих переменных X.
 Интерпретация условий (условие 2) Хj – детерминированные константы, т. е. значения Хj в каждом наблюдении считается экзогенным, полностью определяемым внешними причинами. Такое предположение подразумевает то, что переменная Х полностью контролируется исследователем, который может изменять ее значение в целях эксперимента.
Интерпретация условий (условие 2) Хj – детерминированные константы, т. е. значения Хj в каждом наблюдении считается экзогенным, полностью определяемым внешними причинами. Такое предположение подразумевает то, что переменная Х полностью контролируется исследователем, который может изменять ее значение в целях эксперимента.
 Интерпретация условий (условие 3) Это условие состоит в том, что математическое ожидание случайного члена равно нулю в любом наблюдении. Иногда случайный член бывает положительным, иногда отрицательным, но он не должен иметь смещения ни в одном возможном направлении. Если в уравнение включается постоянный член, то бывает разумным предположить, что первое условие выполняется автоматически, т. к. роль константы и состоит в определении любой систематической составляющей в Y, которую не учитывают объясняющие переменные (если спецификация модели выбрана правильно)
Интерпретация условий (условие 3) Это условие состоит в том, что математическое ожидание случайного члена равно нулю в любом наблюдении. Иногда случайный член бывает положительным, иногда отрицательным, но он не должен иметь смещения ни в одном возможном направлении. Если в уравнение включается постоянный член, то бывает разумным предположить, что первое условие выполняется автоматически, т. к. роль константы и состоит в определении любой систематической составляющей в Y, которую не учитывают объясняющие переменные (если спецификация модели выбрана правильно)
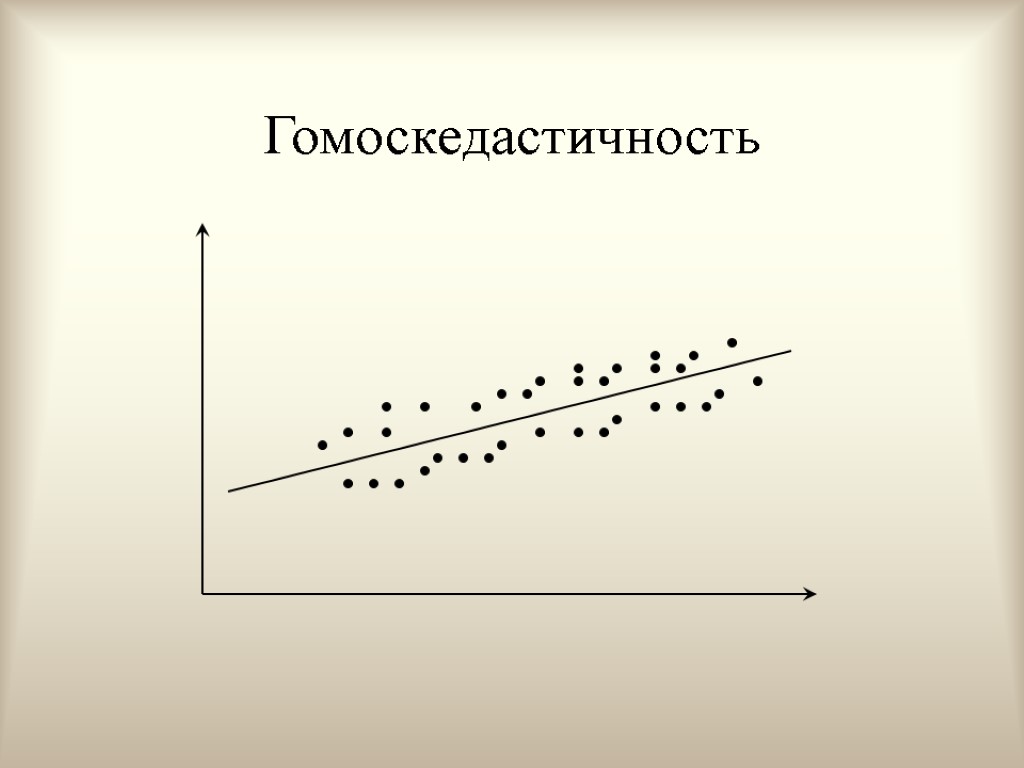
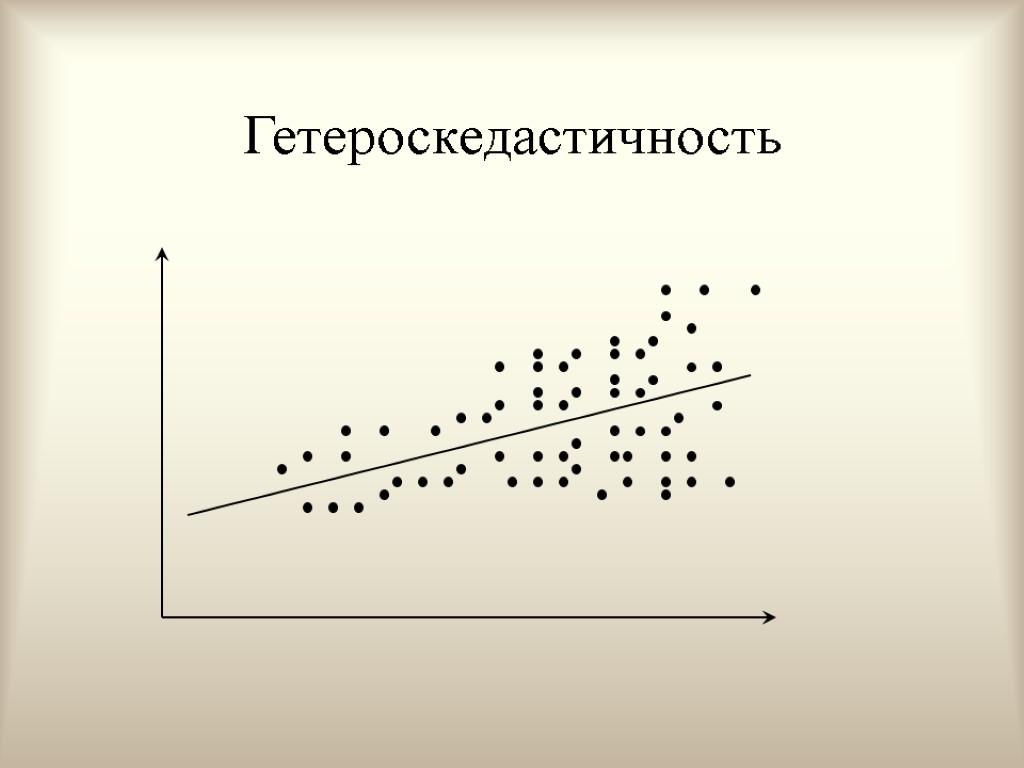
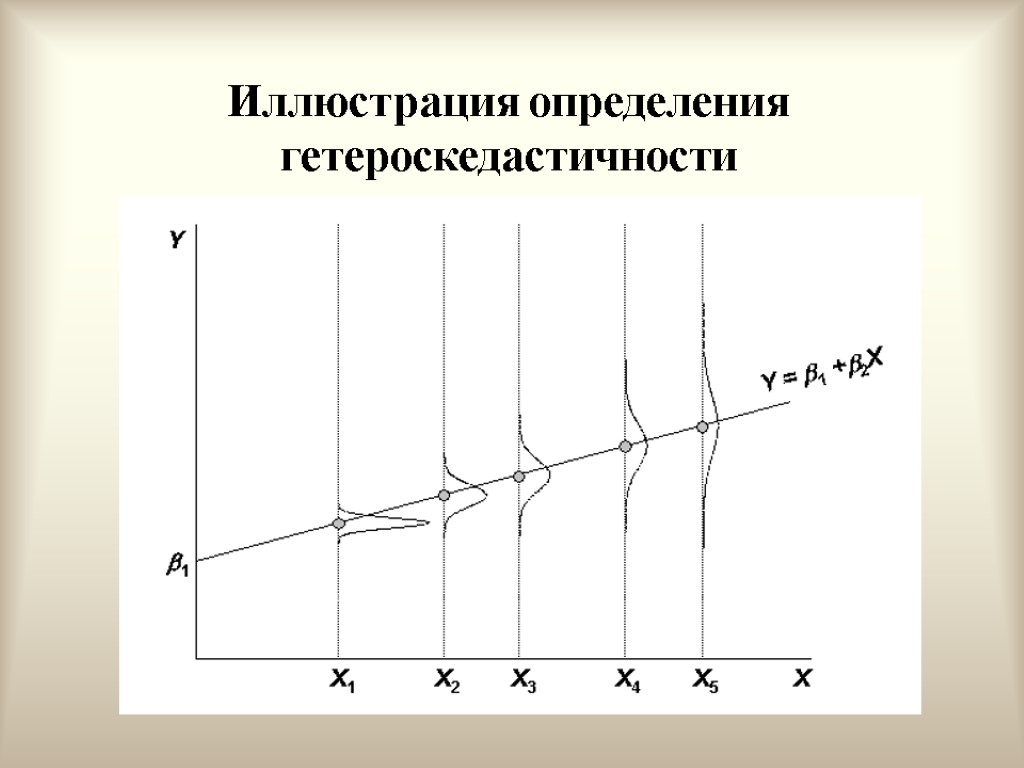
 Интерпретация условий (условие 4) Иногда случайный член будет больше, иногда меньше, но не должно быть априорной причины для того, чтобы он порождал большую ошибку в одних наблюдениях, чем в других. Условие независимости ошибок от номера наблюдения называют гомоскедастичностью. Случай, когда условие гомоскедастичности нарушается, называется гетероскедастичностью.
Интерпретация условий (условие 4) Иногда случайный член будет больше, иногда меньше, но не должно быть априорной причины для того, чтобы он порождал большую ошибку в одних наблюдениях, чем в других. Условие независимости ошибок от номера наблюдения называют гомоскедастичностью. Случай, когда условие гомоскедастичности нарушается, называется гетероскедастичностью.
 Гомоскедастичность
Гомоскедастичность
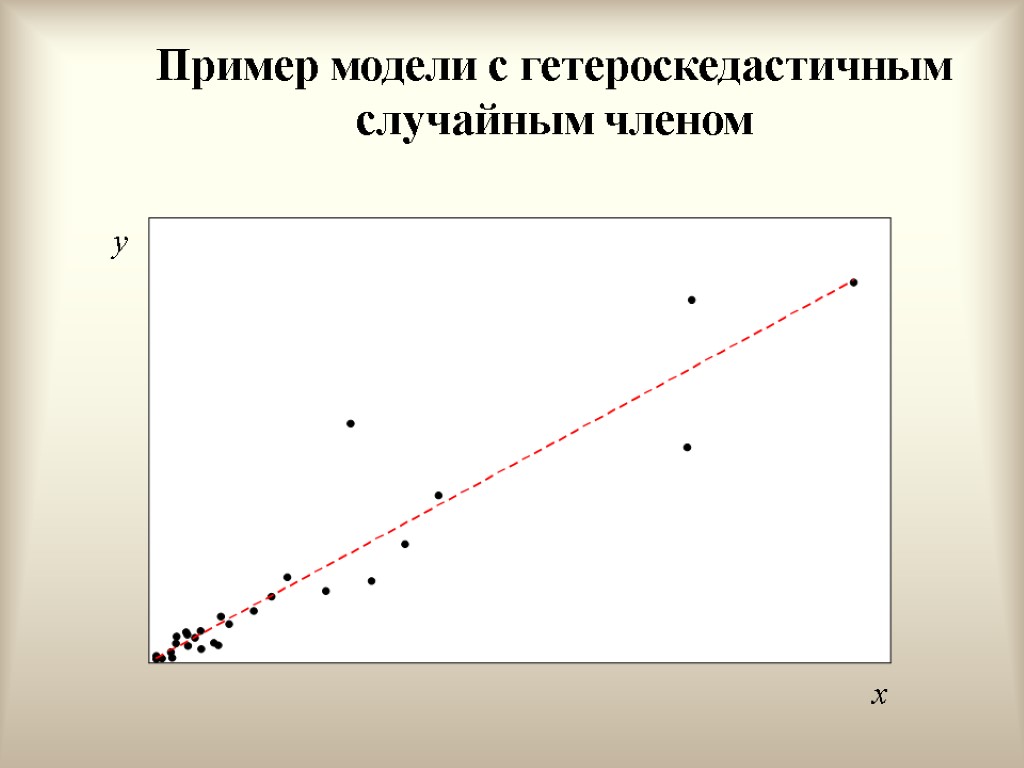
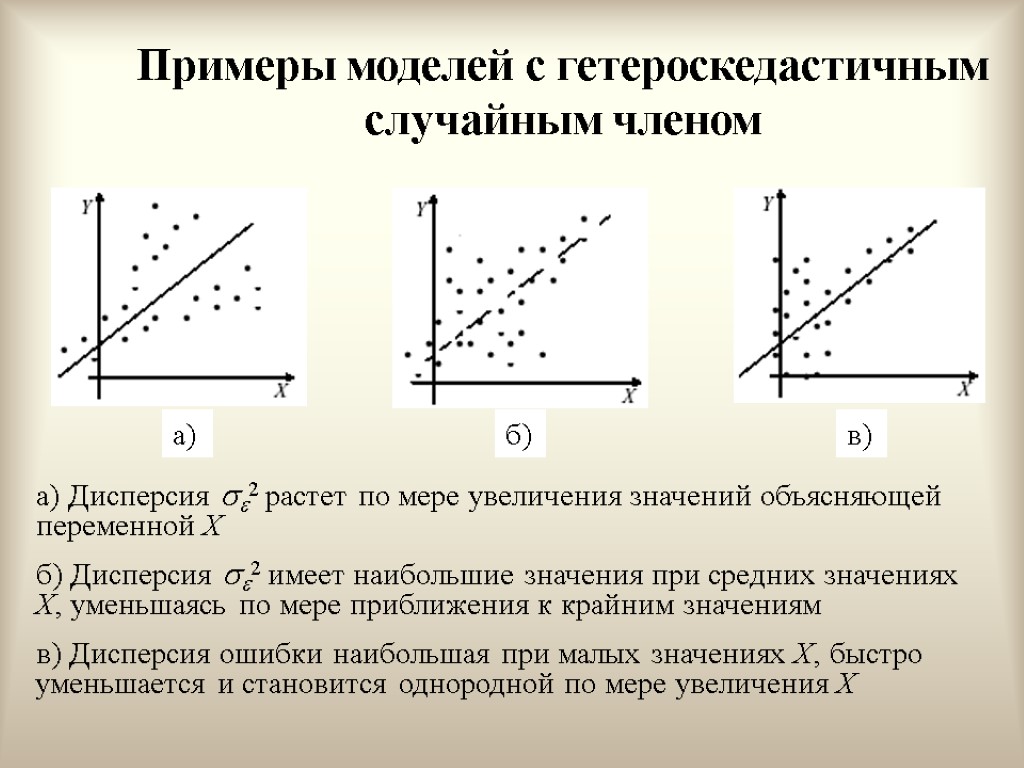
 Гетероскедастичность
Гетероскедастичность
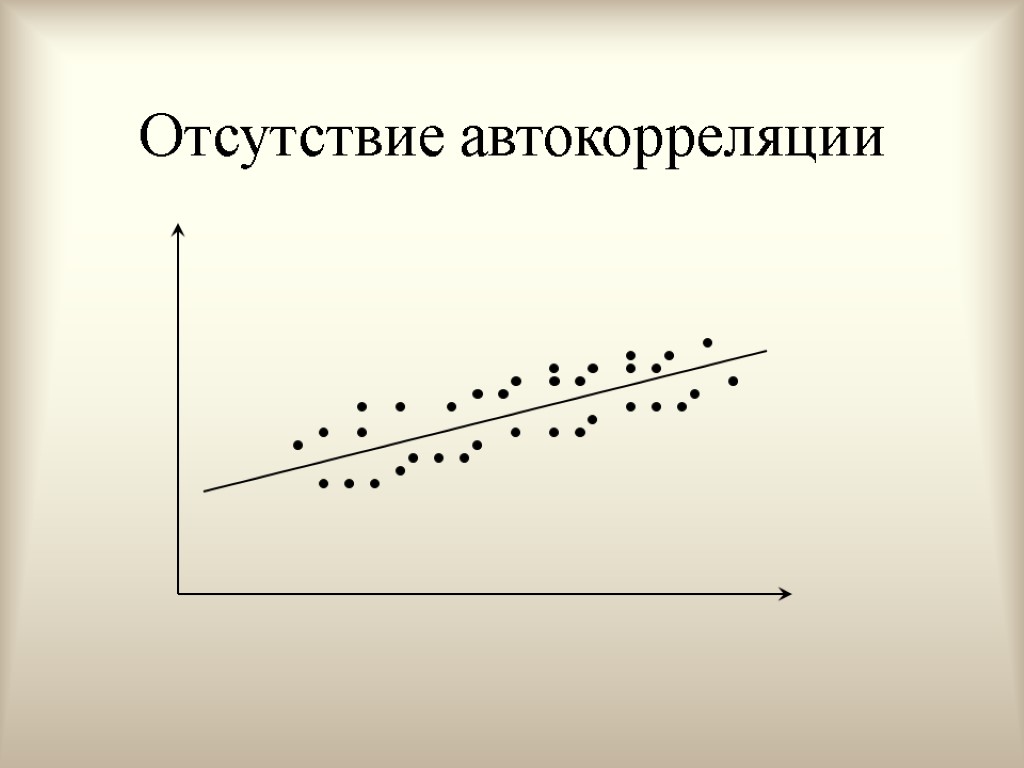
 Интерпретация условий (условие 5) Условие указывает на некоррелированность ошибок для разных наблюдений. Условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях.
Интерпретация условий (условие 5) Условие указывает на некоррелированность ошибок для разных наблюдений. Условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях.
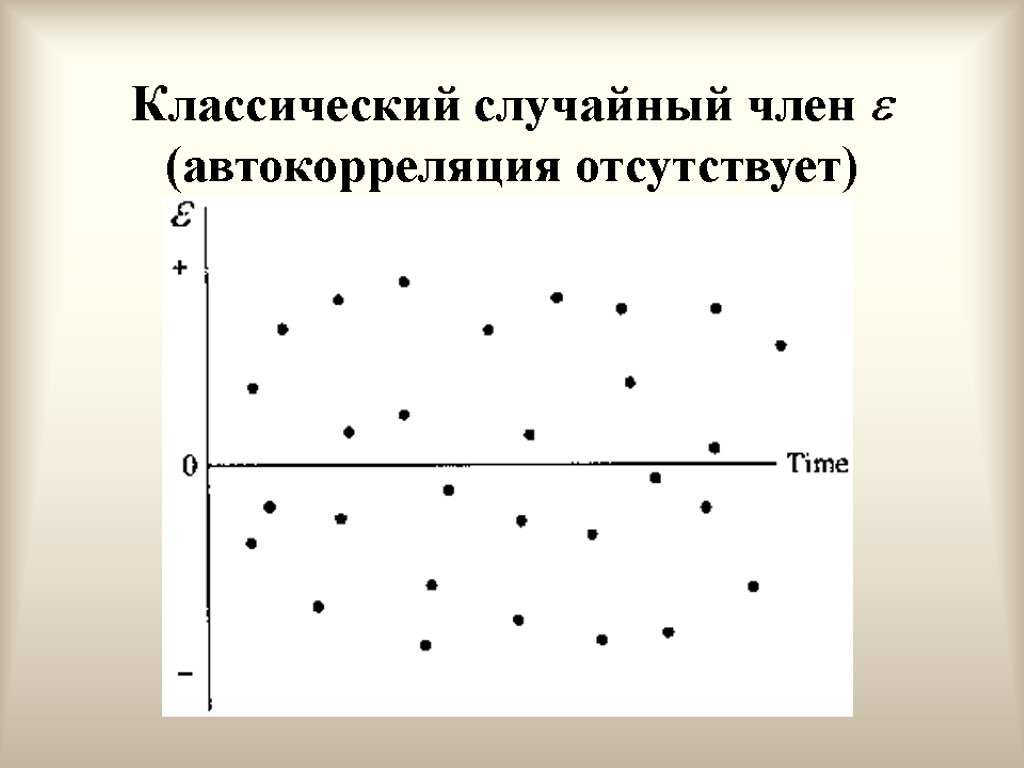
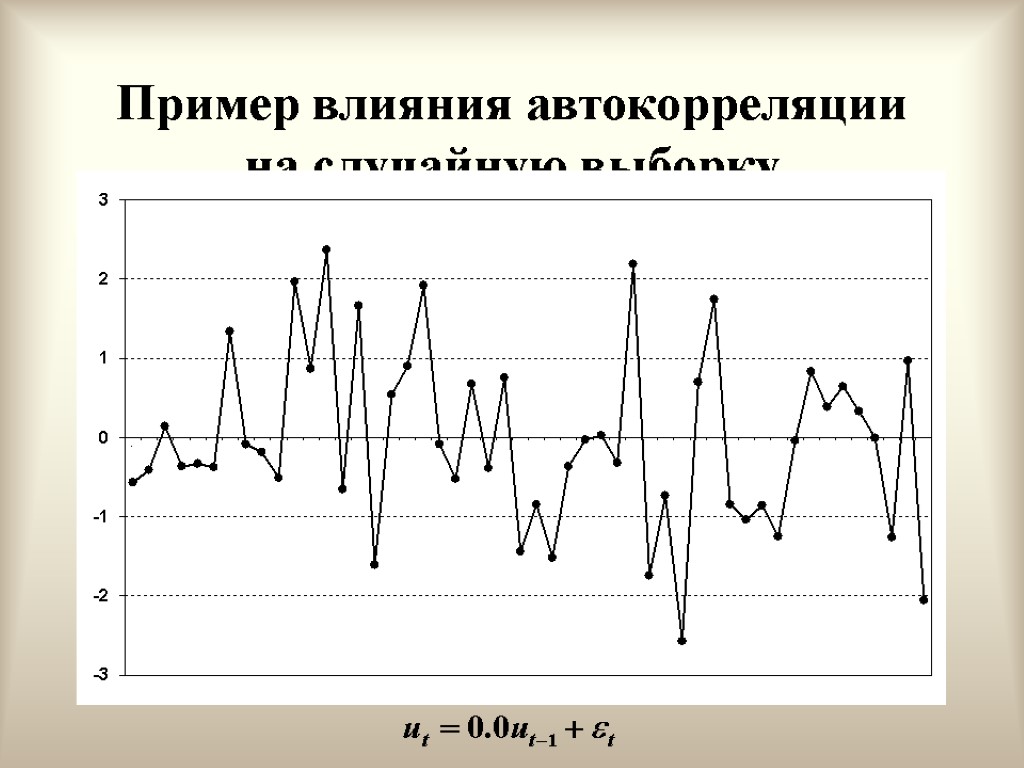
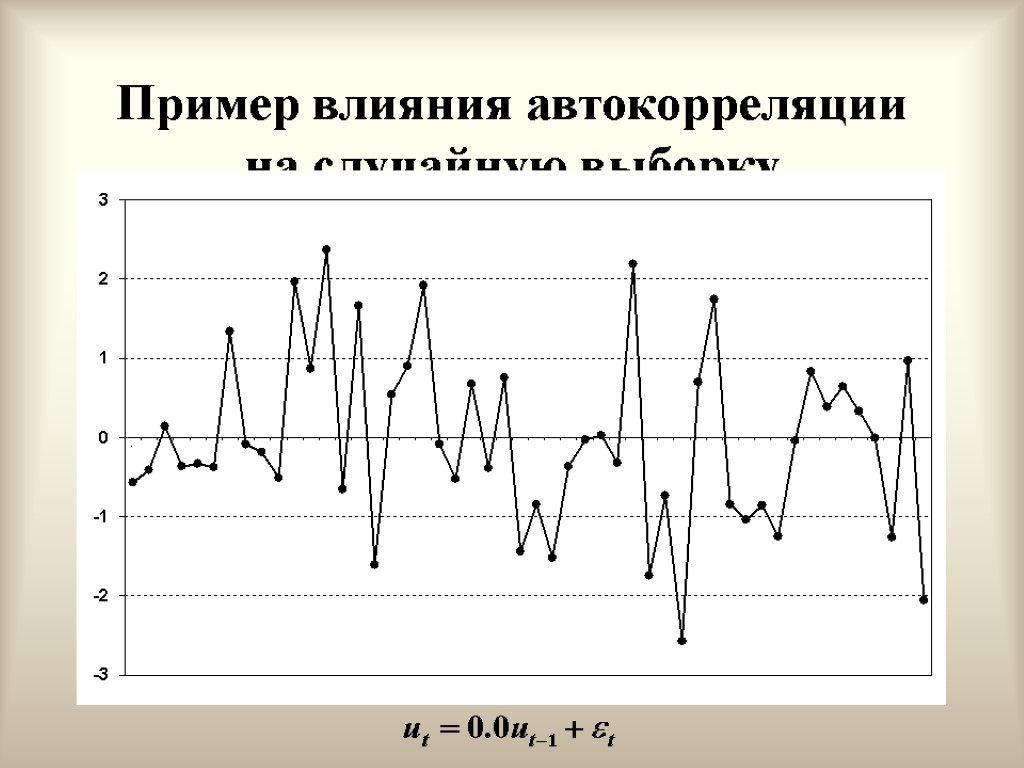
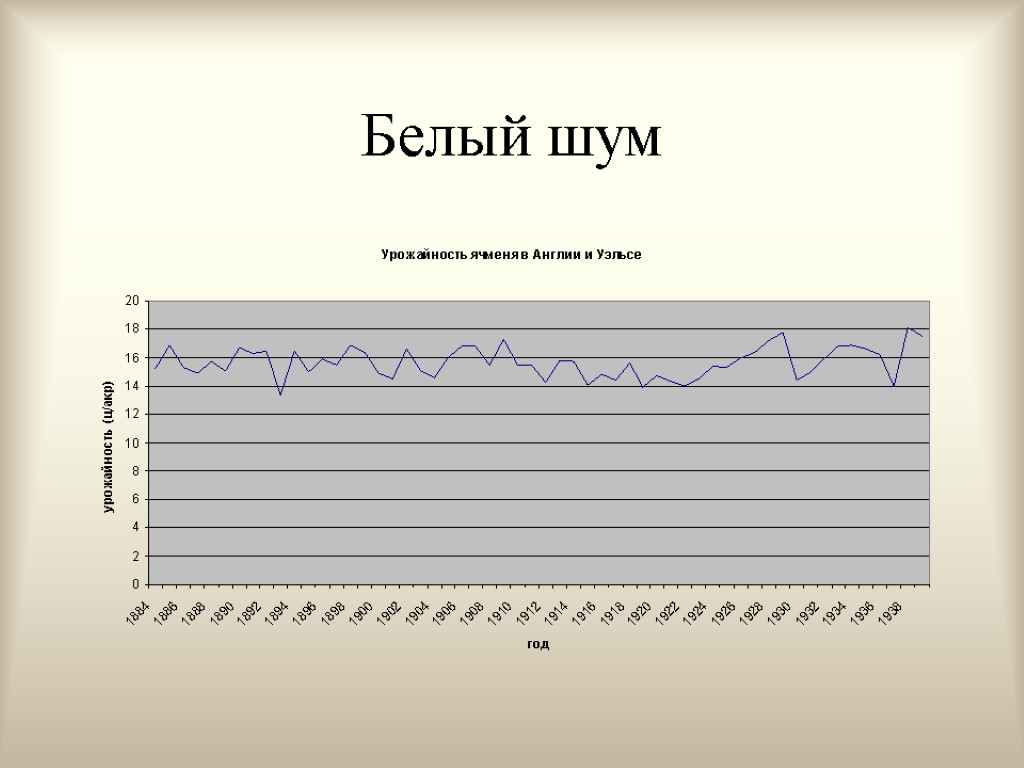
 Отсутствие автокорреляции
Отсутствие автокорреляции
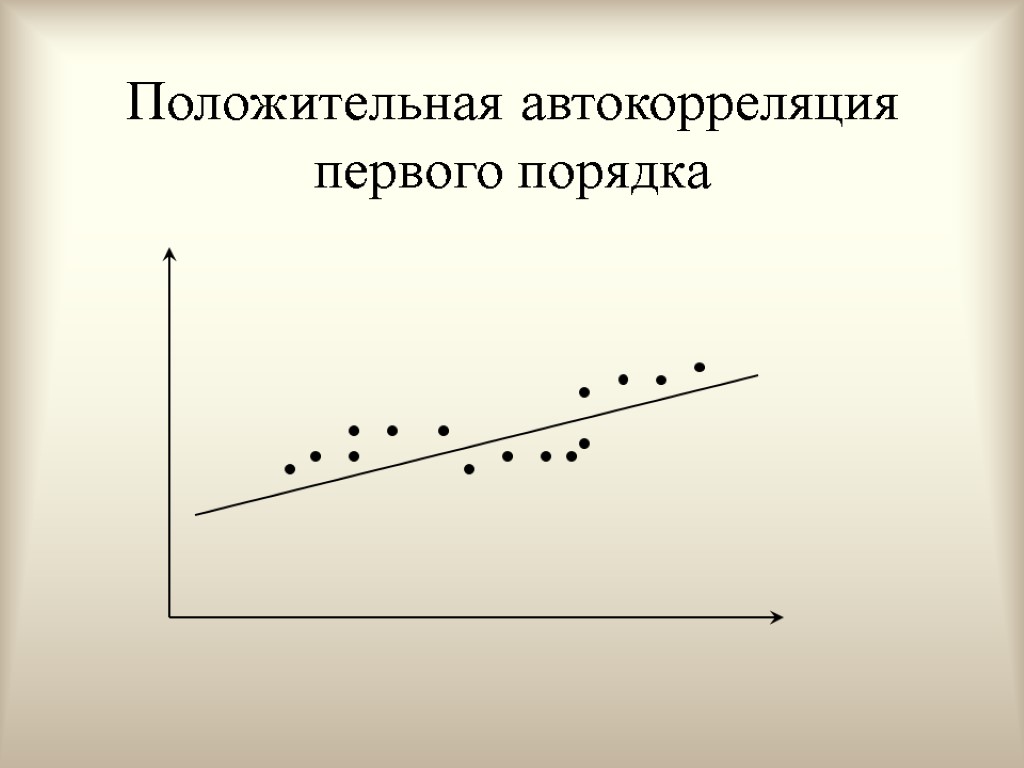
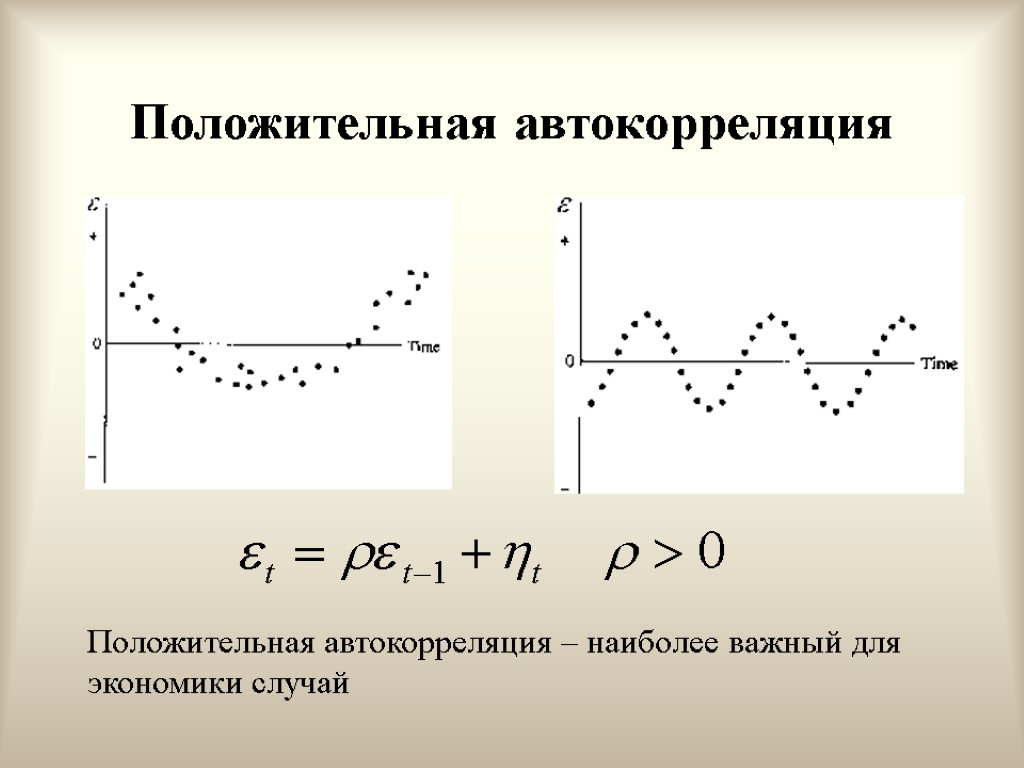
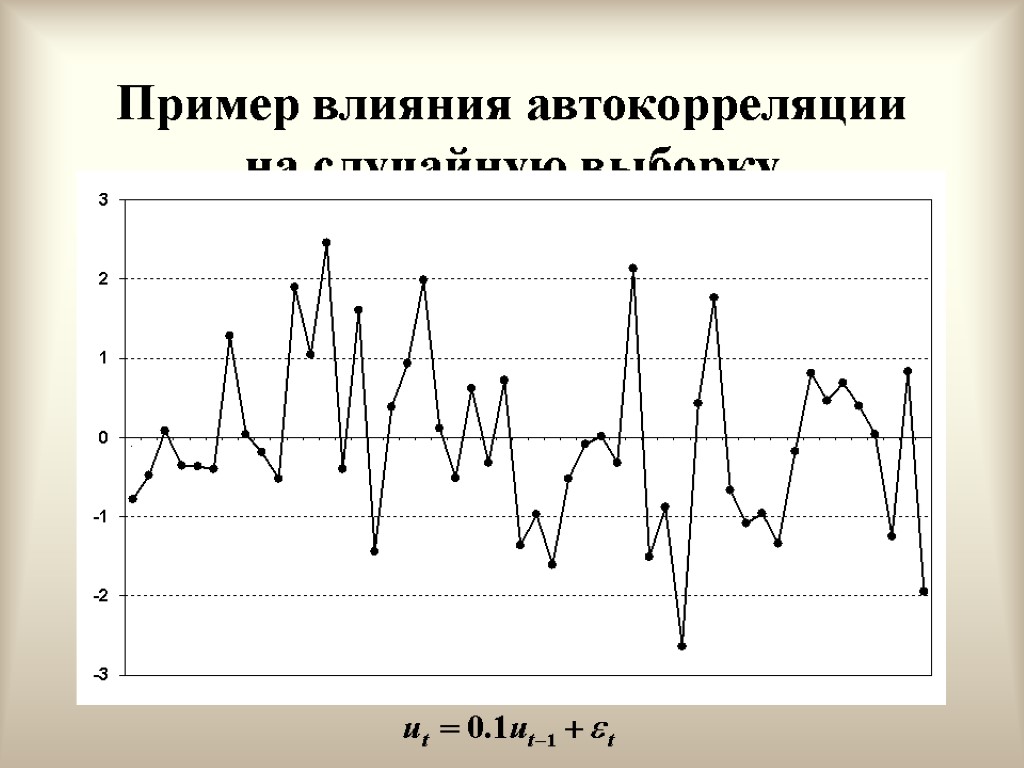
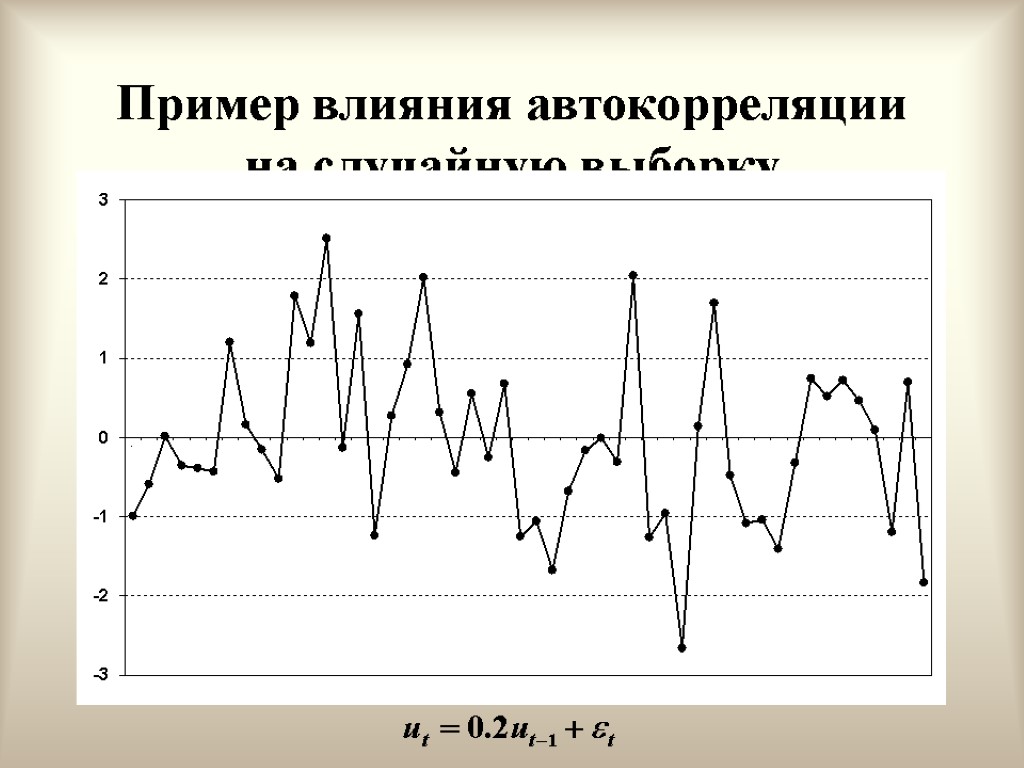
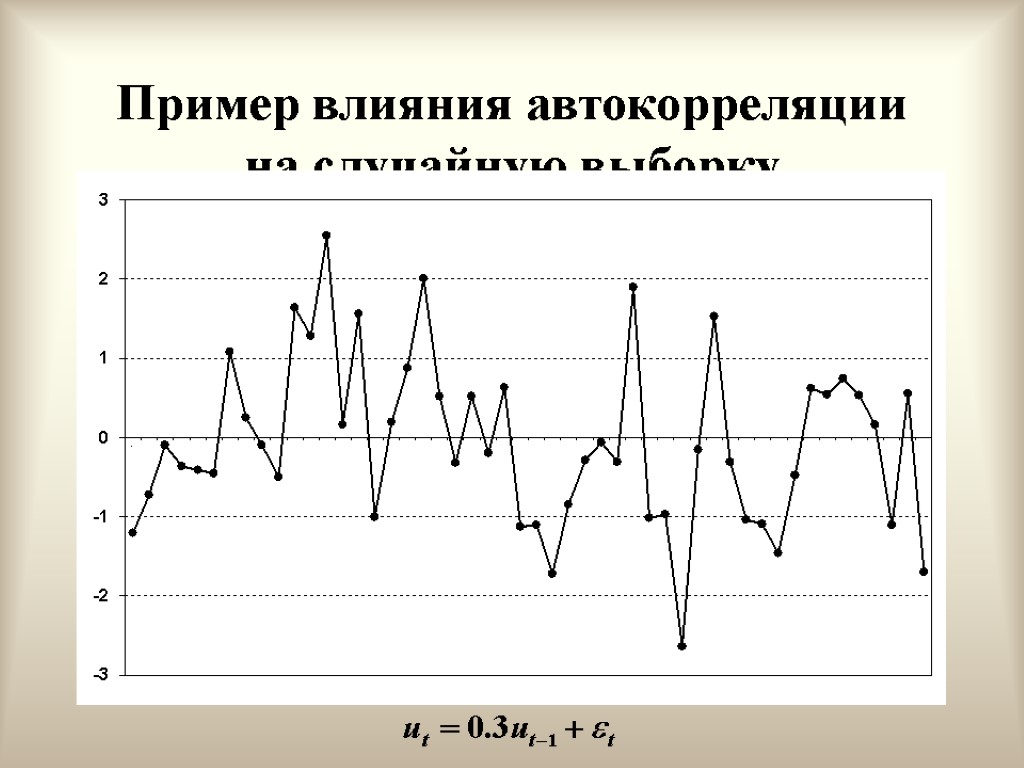
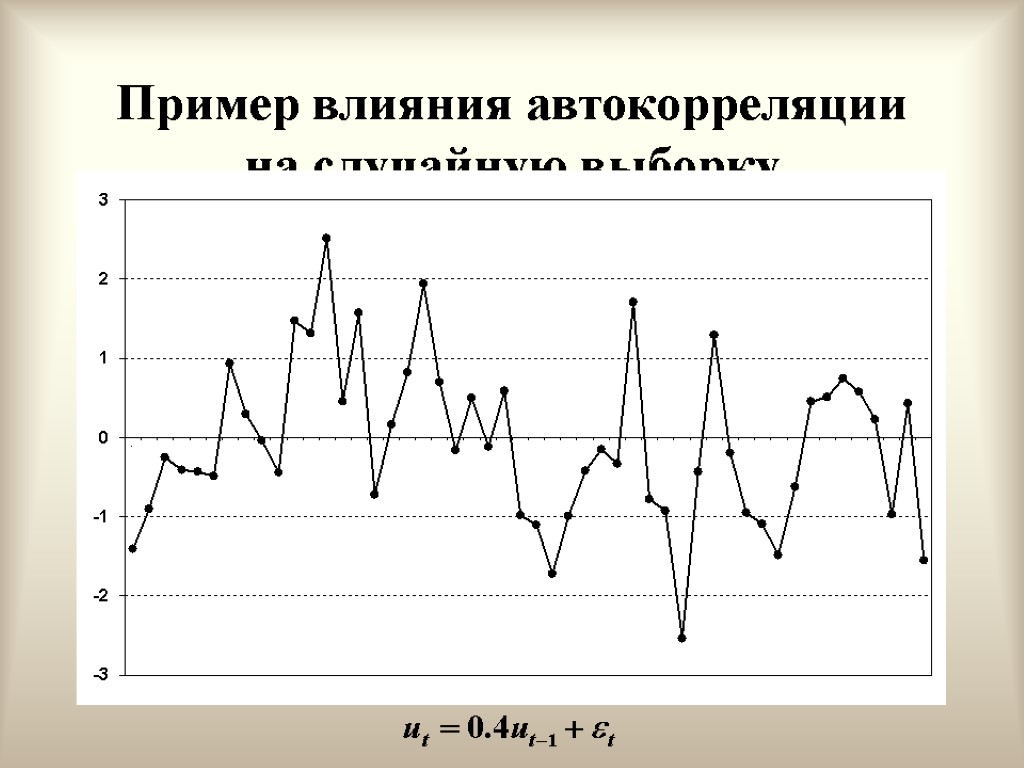
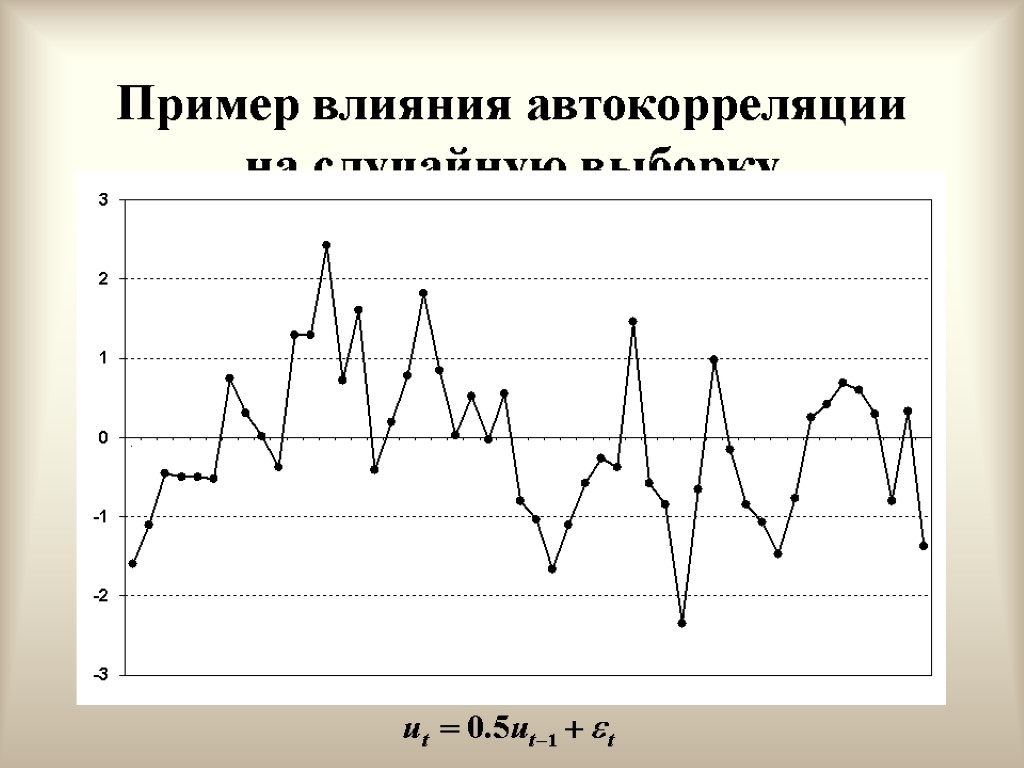
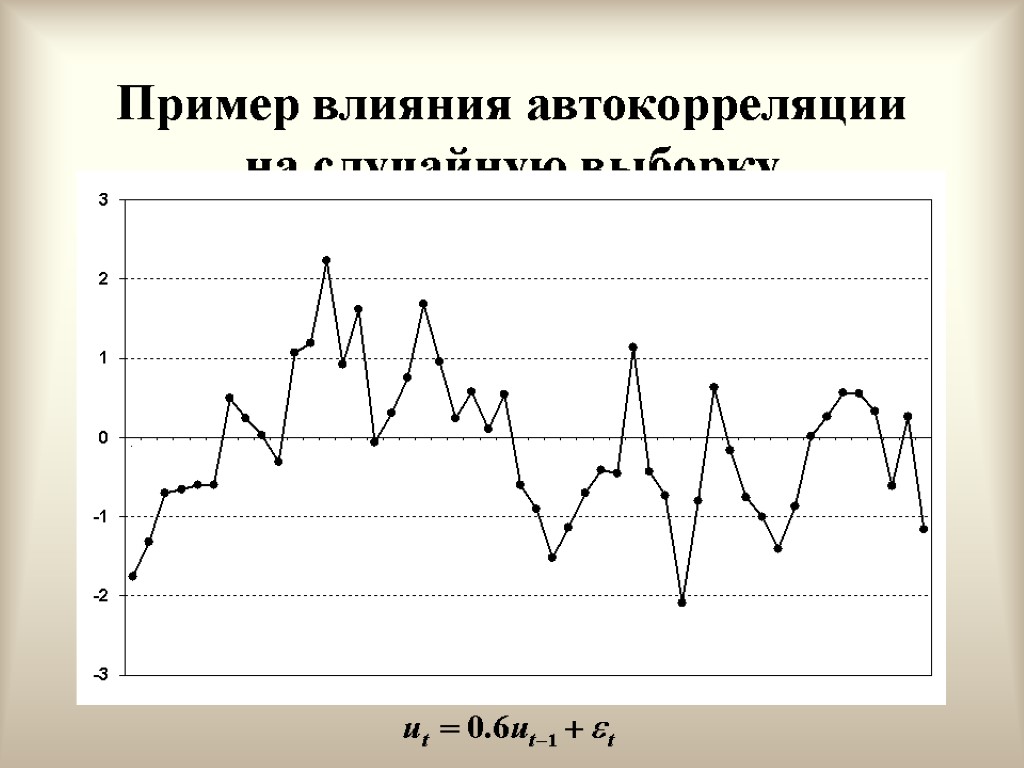
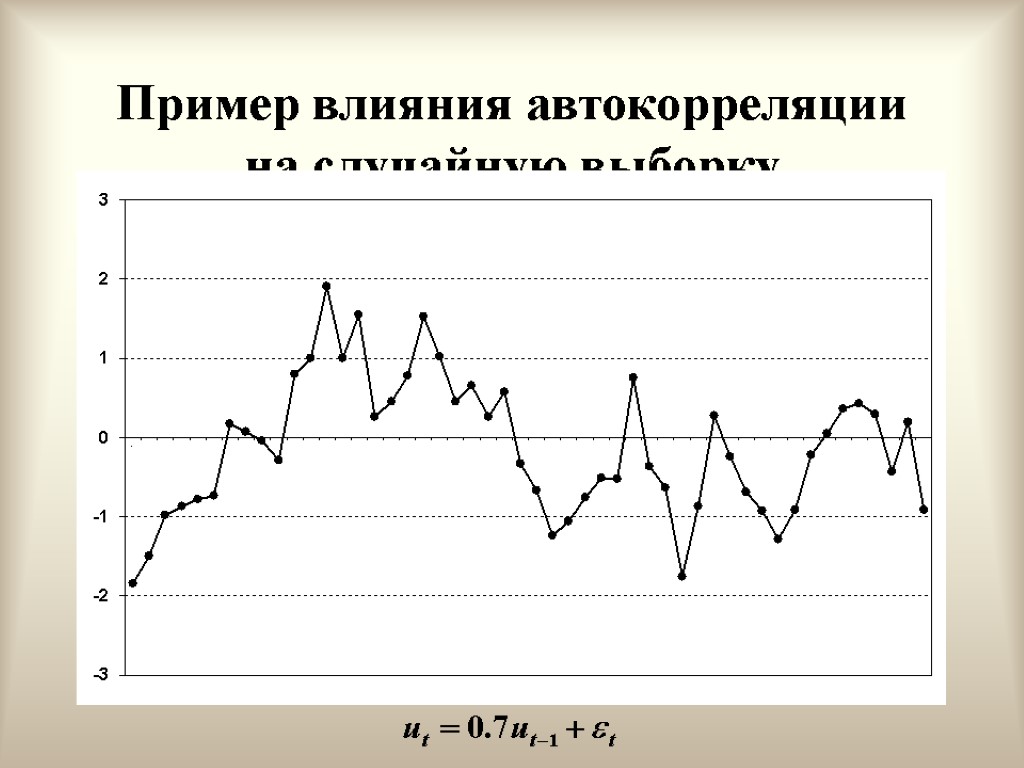
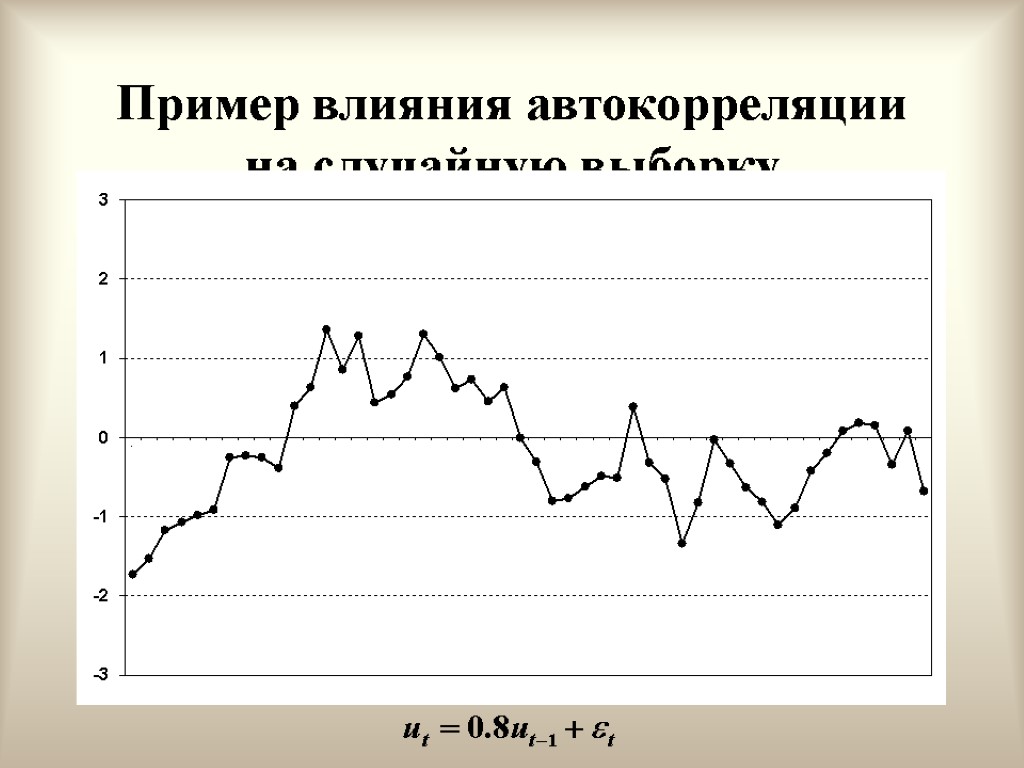
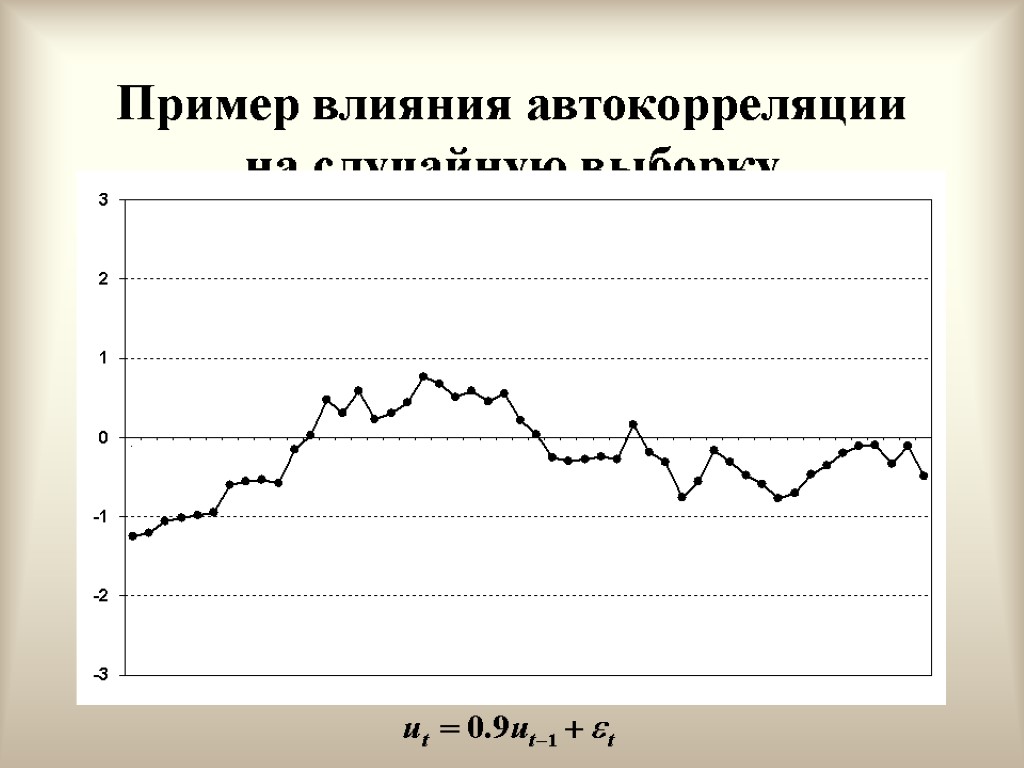
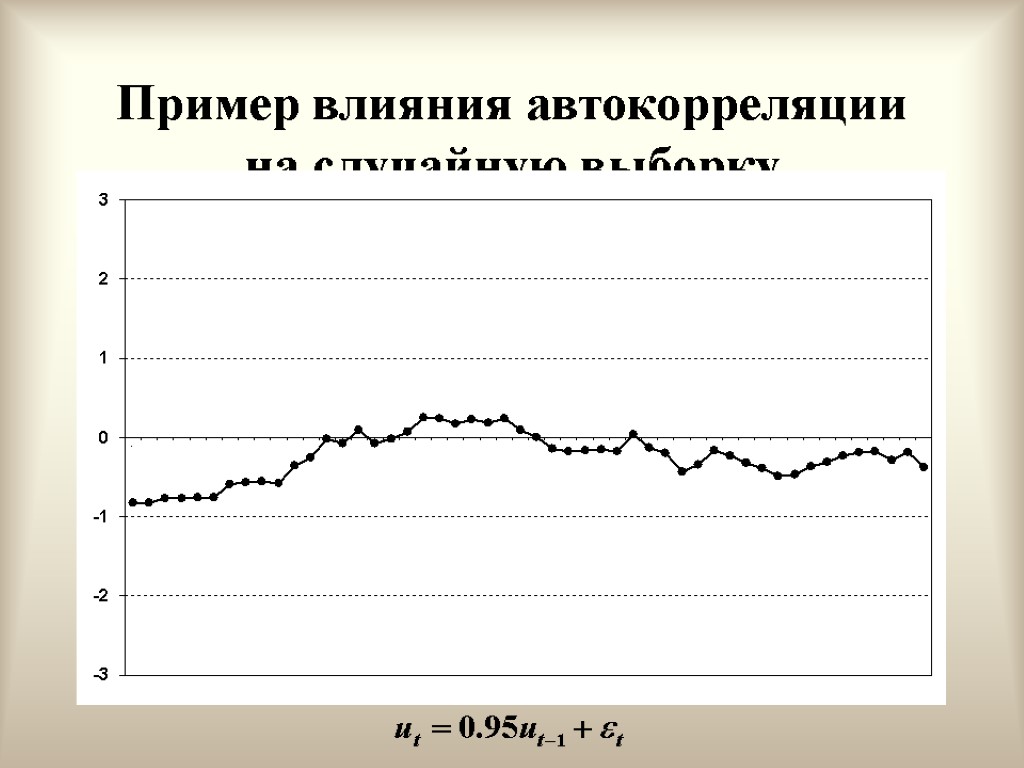
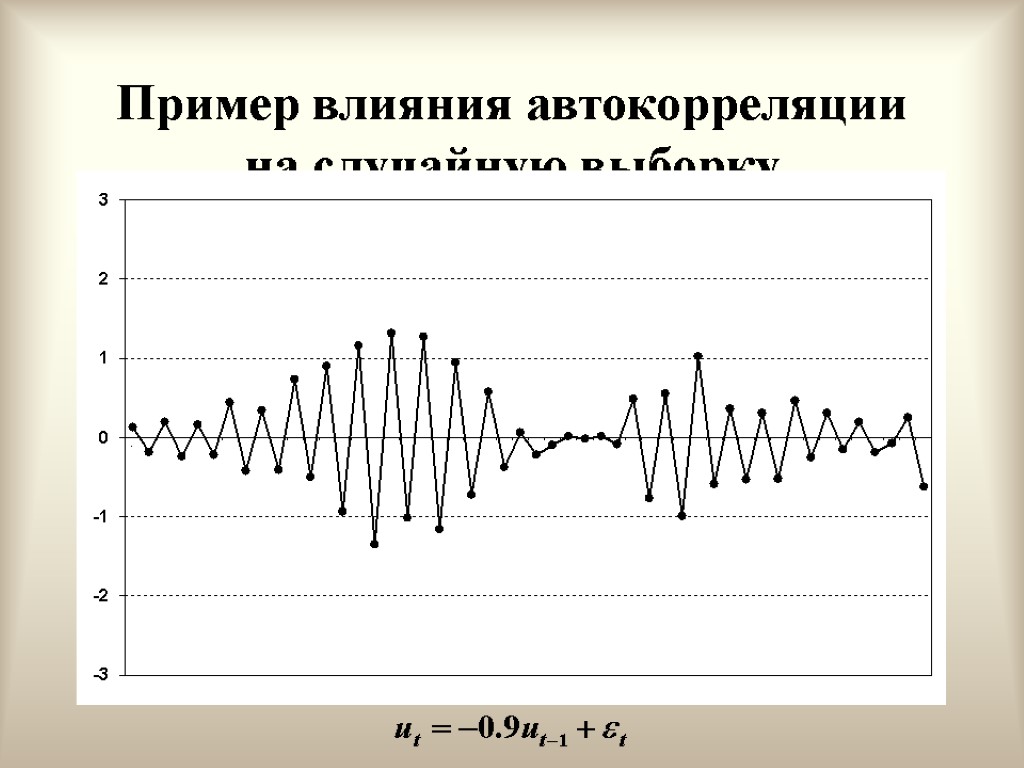
 Положительная автокорреляция первого порядка
Положительная автокорреляция первого порядка
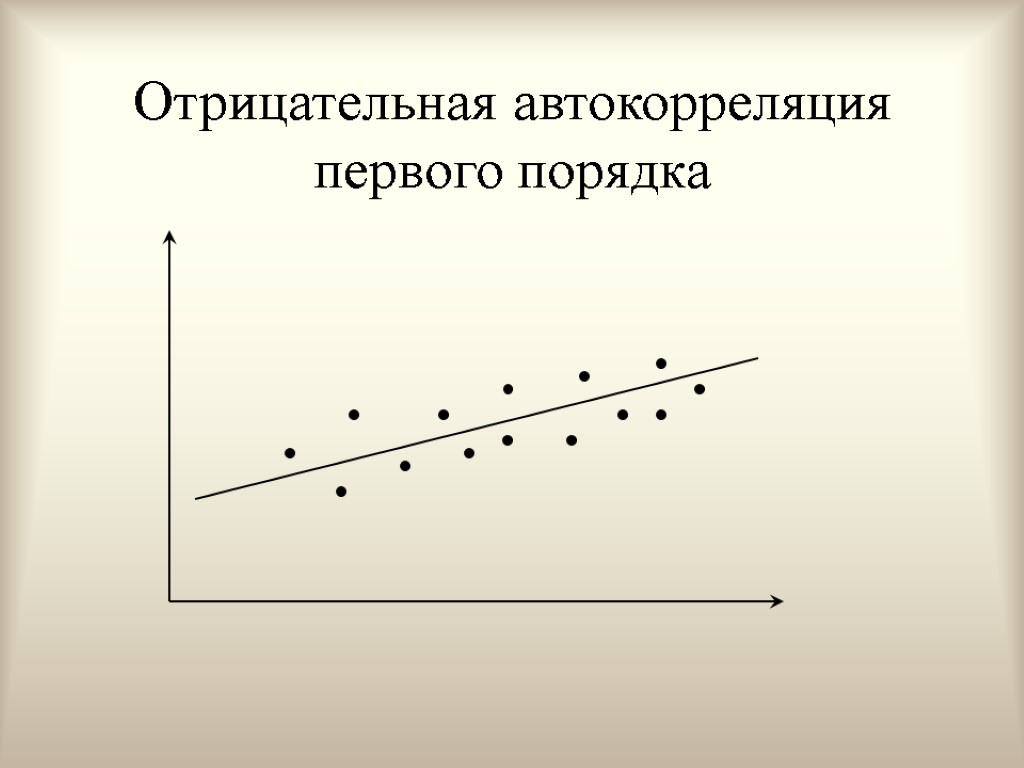
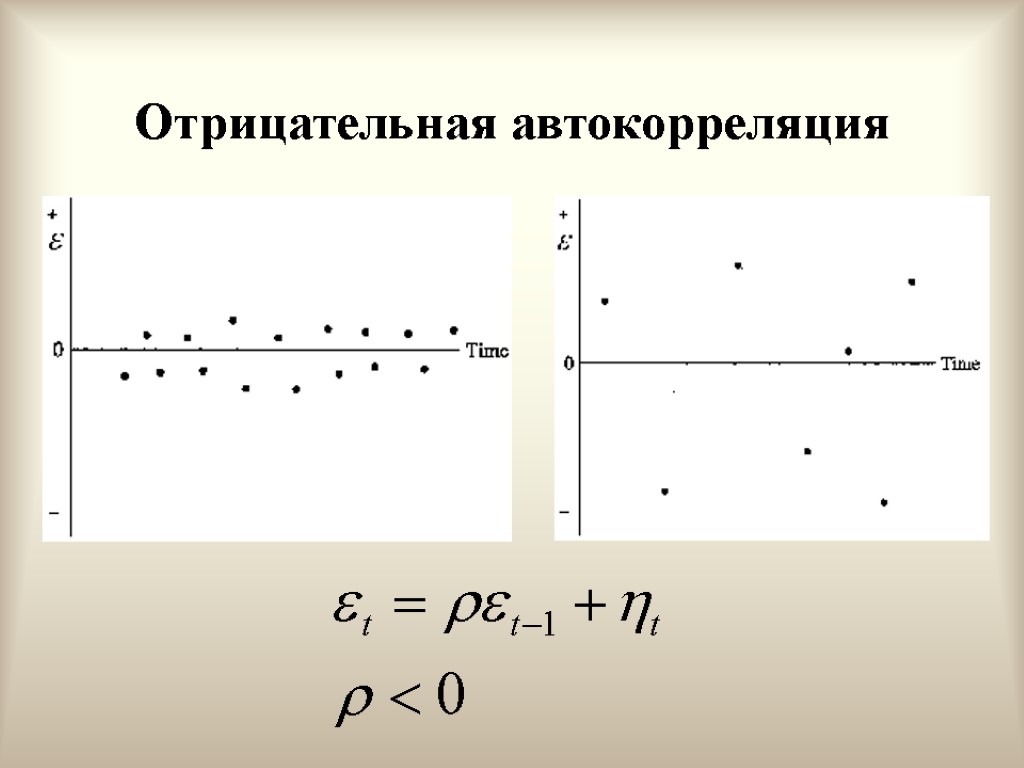
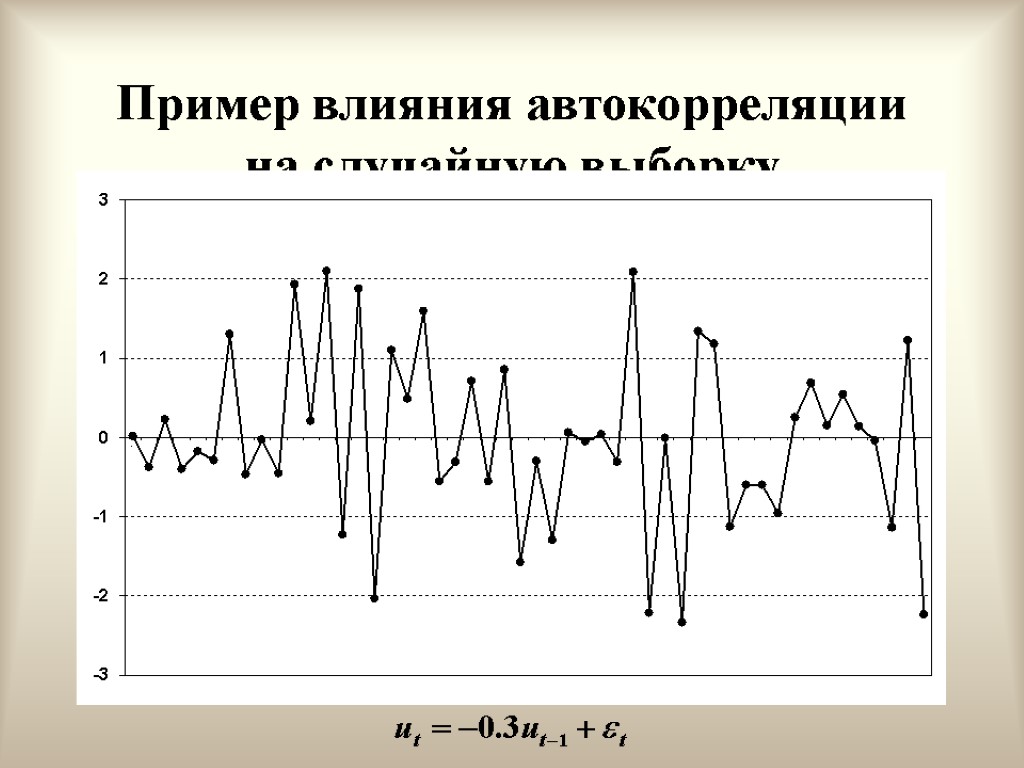
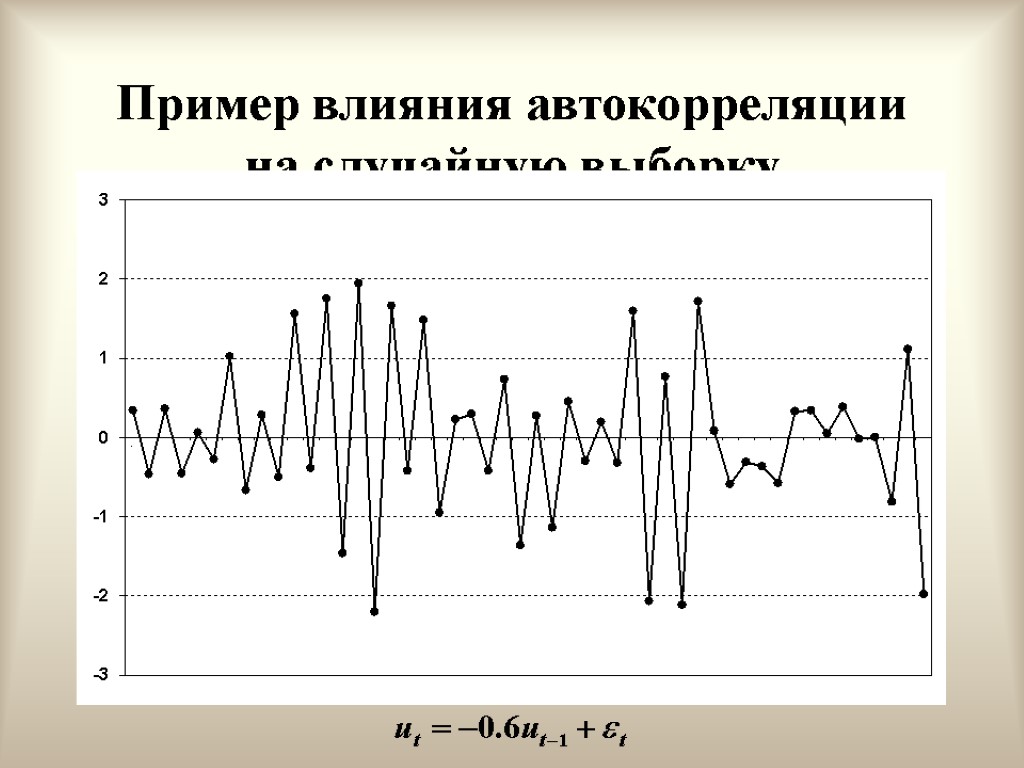
 Отрицательная автокорреляция первого порядка
Отрицательная автокорреляция первого порядка
 Интерпретация условий (условие 6) Нормальность ошибок Ошибки являются суммарным влиянием переменных, невключенных в регрессионное уравнение. Отсюда, как следует из центральной предельной теоремы Ляпунова, при выполнении определенных условий i будут иметь почти нормальное распределение. Отметим, что в случае КЛРМ условие 5 эквивалентно условию статистической независимости ошибок для разных наблюдений. Действительно, если две нормально распределенные величины не коррелированны, то они независимы. В общем случае это не выполняется.
Интерпретация условий (условие 6) Нормальность ошибок Ошибки являются суммарным влиянием переменных, невключенных в регрессионное уравнение. Отсюда, как следует из центральной предельной теоремы Ляпунова, при выполнении определенных условий i будут иметь почти нормальное распределение. Отметим, что в случае КЛРМ условие 5 эквивалентно условию статистической независимости ошибок для разных наблюдений. Действительно, если две нормально распределенные величины не коррелированны, то они независимы. В общем случае это не выполняется.
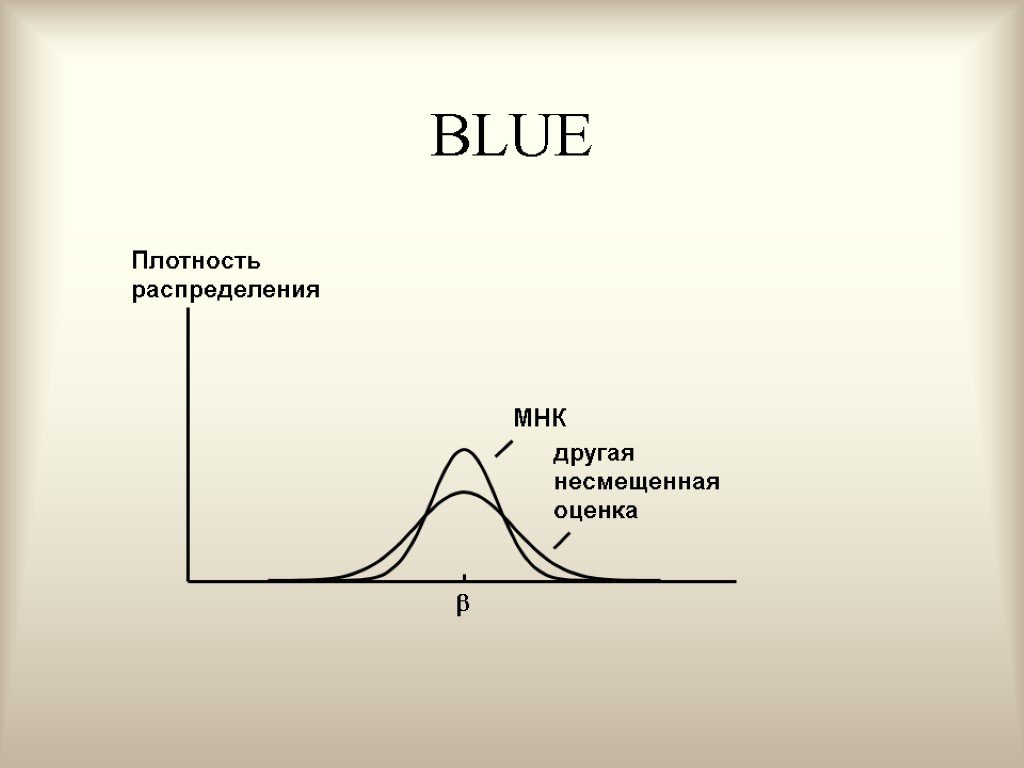
 Теорема Гаусса - Маркова В условиях 1-5 МНК-оценки МЛРМ представляют собой наилучшие линейные несмещенные оценки, т. е. в классе линейных несмещенных оценок МНК-оценки обладают наименьшей дисперсией. Best Linear Unbaised Estimation (BLUE)
Теорема Гаусса - Маркова В условиях 1-5 МНК-оценки МЛРМ представляют собой наилучшие линейные несмещенные оценки, т. е. в классе линейных несмещенных оценок МНК-оценки обладают наименьшей дисперсией. Best Linear Unbaised Estimation (BLUE)
 BLUE
BLUE
 Распределение МНК-коэффициентов Математическое ожидание Дисперсия, где ajj - j-й диагональный элемент матрицы Матрица ковариаций Закон распределения (в случае дополнительного выполнения условия 6))
Распределение МНК-коэффициентов Математическое ожидание Дисперсия, где ajj - j-й диагональный элемент матрицы Матрица ковариаций Закон распределения (в случае дополнительного выполнения условия 6))
 Оценка параметров распределения - несмещенная состоятельная оценка дисперсии ошибок - состоятельная оценка дисперсии коэффициентов - состоятельная оценка матрицы ковариаций коэффициентов
Оценка параметров распределения - несмещенная состоятельная оценка дисперсии ошибок - состоятельная оценка дисперсии коэффициентов - состоятельная оценка матрицы ковариаций коэффициентов
 Стандартные ошибки коэффициентов стандартная ошибка регрессии стандартные ошибки коэффициентов
Стандартные ошибки коэффициентов стандартная ошибка регрессии стандартные ошибки коэффициентов
 Вопросы для повторения Какие вы знаете свойства статистических оценок. Какие свойства относятся к асимптотическим свойствам оценок. Перечислите условия Гаусса-Маркова. Каков содержательный смысл условия гомоскедастичночти. Каков содержательный смысл условия отсутствия автокорреляции ошибок. Какие условия Гаусса Маркова используются при доказательстве несмещенности МНК-коэффициентов. Какие условия Гаусса Маркова используются при доказательстве эффективности МНК-коэффициентов. Что произойдет, если математическое ожидание ошибки уравненяи будет отлично от нуля. Где используется предположение о нормальности ошибок. Что такое стандартная ошибка регрессии, стандартная ошибка коэффициента. Согласны ли вы с тем, что несмещенная оценка всегда лучше, чем смещенная. Сформулируйте теорему Гаусса-Маркова
Вопросы для повторения Какие вы знаете свойства статистических оценок. Какие свойства относятся к асимптотическим свойствам оценок. Перечислите условия Гаусса-Маркова. Каков содержательный смысл условия гомоскедастичночти. Каков содержательный смысл условия отсутствия автокорреляции ошибок. Какие условия Гаусса Маркова используются при доказательстве несмещенности МНК-коэффициентов. Какие условия Гаусса Маркова используются при доказательстве эффективности МНК-коэффициентов. Что произойдет, если математическое ожидание ошибки уравненяи будет отлично от нуля. Где используется предположение о нормальности ошибок. Что такое стандартная ошибка регрессии, стандартная ошибка коэффициента. Согласны ли вы с тем, что несмещенная оценка всегда лучше, чем смещенная. Сформулируйте теорему Гаусса-Маркова
 Тема 7. Проверка гипотез относительно возможных значений коэффициентов МЛРМ
Тема 7. Проверка гипотез относительно возможных значений коэффициентов МЛРМ
 Темы лекции Проверка гипотезы о незначимости регрессии в целом Проверка гипотезы о равенстве коэффициента регрессионного уравнения некоторому числу Проверка гипотезы об одновременном равенстве нулю q коэффициентов регрессионного уравнения Проверка гипотезы о наличии линейных ограничений на коэффициенты Тест Чоу
Темы лекции Проверка гипотезы о незначимости регрессии в целом Проверка гипотезы о равенстве коэффициента регрессионного уравнения некоторому числу Проверка гипотезы об одновременном равенстве нулю q коэффициентов регрессионного уравнения Проверка гипотезы о наличии линейных ограничений на коэффициенты Тест Чоу
 Проверка гипотезы о незначимости регрессии в целом статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Фишера с числом степеней свободы числителя k и знаменателя N-k-1 Критическую точку находим из таблиц распределения Фишера для выбранного уровня значимости и числу степеней свободы числителя k и знаменателя N-k-1 если , мы нулевую гипотезу отвергаем
Проверка гипотезы о незначимости регрессии в целом статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Фишера с числом степеней свободы числителя k и знаменателя N-k-1 Критическую точку находим из таблиц распределения Фишера для выбранного уровня значимости и числу степеней свободы числителя k и знаменателя N-k-1 если , мы нулевую гипотезу отвергаем
 Проверка гипотезы о равенстве коэффициента регрессионного уравнения некоторому числу статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Стьюдента с числом степеней свободы N-k-1 Критическую точку находим из таблиц критических точек распределения Стьюдента с N-k-1 степенями свободы для выбранного уровня значимости и учитывая, что критическая область двусторонняя если , мы нулевую гипотезу отвергаем H0: j = j0 Hа: j j0
Проверка гипотезы о равенстве коэффициента регрессионного уравнения некоторому числу статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Стьюдента с числом степеней свободы N-k-1 Критическую точку находим из таблиц критических точек распределения Стьюдента с N-k-1 степенями свободы для выбранного уровня значимости и учитывая, что критическая область двусторонняя если , мы нулевую гипотезу отвергаем H0: j = j0 Hа: j j0
 Проверка гипотезы о незначимом отличии от нуля коэффициента регрессионного уравнения статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Стьюдента с числом степеней свободы N-k-1 Критическую точку находим из таблиц критических точек распределения Стьюдента с N-k-1 степенями свободы для выбранного уровня значимости и учитывая, что критическая область двусторонняя если , мы нулевую гипотезу отвергаем H0: j = 0 Hа: j 0 t - статистика j-го коэффициента МЛРМ
Проверка гипотезы о незначимом отличии от нуля коэффициента регрессионного уравнения статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Стьюдента с числом степеней свободы N-k-1 Критическую точку находим из таблиц критических точек распределения Стьюдента с N-k-1 степенями свободы для выбранного уровня значимости и учитывая, что критическая область двусторонняя если , мы нулевую гипотезу отвергаем H0: j = 0 Hа: j 0 t - статистика j-го коэффициента МЛРМ
 Значимость коэффициента регрессионного уравнения t-тесты обеспечивают проверку значимости предельного вклада каждой переменной при допущении, что все остальные переменные уже включены в модель Незначимость коэффициента регрессии не всегда может служить основанием для исключения соответствующей переменной из модели
Значимость коэффициента регрессионного уравнения t-тесты обеспечивают проверку значимости предельного вклада каждой переменной при допущении, что все остальные переменные уже включены в модель Незначимость коэффициента регрессии не всегда может служить основанием для исключения соответствующей переменной из модели
 Регрессия с ограничениями Модель, в которой мы проверяем гипотезу о коэффициентах, называется регрессия без ограничений (unrestricted, UR) Регрессия с ограничениями строится из регрессии без ограничений в предположении, что нулевая гипотеза верна (restricted, R) Сравнение объясняющих способностей регрессии с ограничениями и регрессии без ограничений при помощи F-теста – очень распространенный прием в эконометрике.
Регрессия с ограничениями Модель, в которой мы проверяем гипотезу о коэффициентах, называется регрессия без ограничений (unrestricted, UR) Регрессия с ограничениями строится из регрессии без ограничений в предположении, что нулевая гипотеза верна (restricted, R) Сравнение объясняющих способностей регрессии с ограничениями и регрессии без ограничений при помощи F-теста – очень распространенный прием в эконометрике.
 Проверка гипотезы об одновременном равенстве нулю q коэффициентов регрессионного уравнения статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Фишера с числом степеней свободы числителя q и знаменателя N-k-1 Критическую точку находим из таблиц распределения Фишера для выбранного уровня значимости и числу степеней свободы числителя q и знаменателя N-k-1 если , мы нулевую гипотезу отвергаем
Проверка гипотезы об одновременном равенстве нулю q коэффициентов регрессионного уравнения статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Фишера с числом степеней свободы числителя q и знаменателя N-k-1 Критическую точку находим из таблиц распределения Фишера для выбранного уровня значимости и числу степеней свободы числителя q и знаменателя N-k-1 если , мы нулевую гипотезу отвергаем
 Проверка гипотезы о наличии линейных ограничений на коэффициенты Пример составления регрессии без ограничений: XL трудовые доходы, XNL нетрудовые доходы, С - потребление q чисто ограничений, накладываемых на коэффициенты -. в нашем случае равно 1
Проверка гипотезы о наличии линейных ограничений на коэффициенты Пример составления регрессии без ограничений: XL трудовые доходы, XNL нетрудовые доходы, С - потребление q чисто ограничений, накладываемых на коэффициенты -. в нашем случае равно 1
 Тест Вальда тестирования линейного ограничения общего вида H0: H = r Например: означает, что статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Пирсона с числом степеней свободы q Критическую точку находим из таблиц распределения Пирсона для выбранного уровня значимости и числу степеней свободы q если , мы нулевую гипотезу отвергаем
Тест Вальда тестирования линейного ограничения общего вида H0: H = r Например: означает, что статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Пирсона с числом степеней свободы q Критическую точку находим из таблиц распределения Пирсона для выбранного уровня значимости и числу степеней свободы q если , мы нулевую гипотезу отвергаем
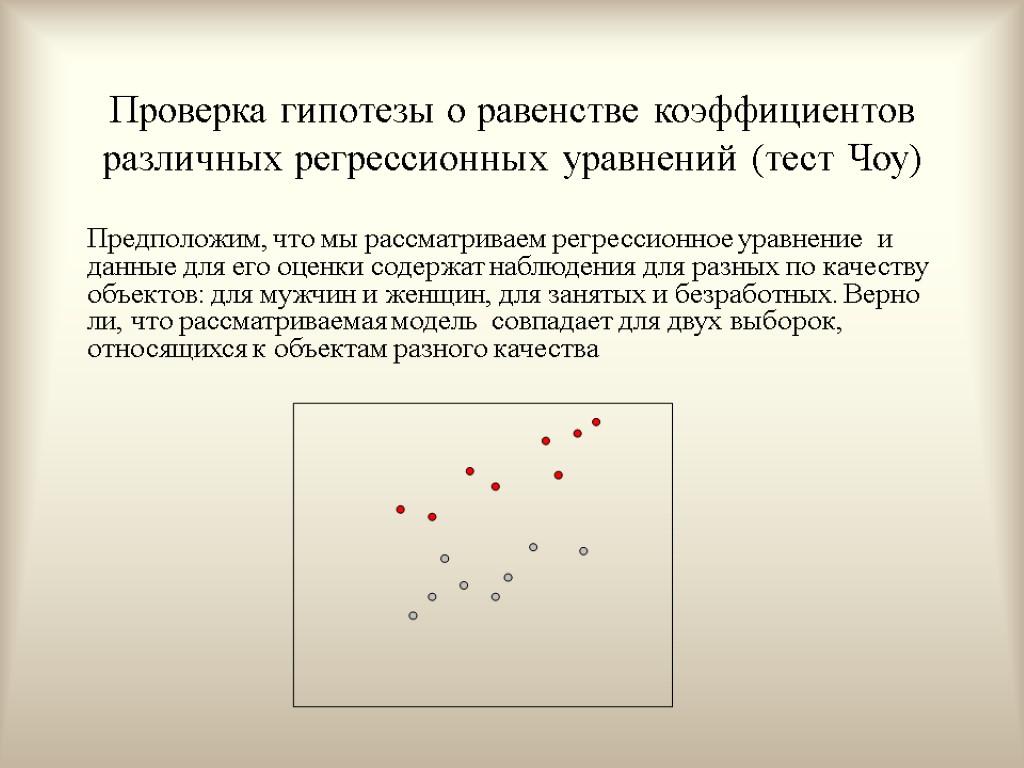
 Проверка гипотезы о равенстве коэффициентов различных регрессионных уравнений (тест Чоу) Предположим, что мы рассматриваем регрессионное уравнение и данные для его оценки содержат наблюдения для разных по качеству объектов: для мужчин и женщин, для занятых и безработных. Верно ли, что рассматриваемая модель совпадает для двух выборок, относящихся к объектам разного качества
Проверка гипотезы о равенстве коэффициентов различных регрессионных уравнений (тест Чоу) Предположим, что мы рассматриваем регрессионное уравнение и данные для его оценки содержат наблюдения для разных по качеству объектов: для мужчин и женщин, для занятых и безработных. Верно ли, что рассматриваемая модель совпадает для двух выборок, относящихся к объектам разного качества
 Проверка гипотезы о равенстве коэффициентов различных регрессионных уравнений (тест Чоу) статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Фишера с числом степеней свободы числителя k и знаменателя N+M-2k Критическую точку находим из таблиц распределения Фишера для выбранного уровня значимости и числу степеней свободы числителя k и знаменателя N+M-2k если , мы нулевую гипотезу отвергаем
Проверка гипотезы о равенстве коэффициентов различных регрессионных уравнений (тест Чоу) статистический критерий При справедливости нулевой гипотезы данная статистика имеет распределение Фишера с числом степеней свободы числителя k и знаменателя N+M-2k Критическую точку находим из таблиц распределения Фишера для выбранного уровня значимости и числу степеней свободы числителя k и знаменателя N+M-2k если , мы нулевую гипотезу отвергаем
 Вопросы для самопроверки Как проверить значимость регрессии в целом. В чем заключается содержательный смысл гипотезы о равенстве коэффициента уравнения нулю. Как провести односторонний тест на равенство коэффициента нулю. В чем смысл доверительного интервала коэффициента. Как проверить гипотезу о равенстве коэффициента уравнения нулю при помощи доверительного интервала.. Как связаны между собой F и t статистика в парной модели. Как проверить гипотезу о равенстве коэффициента уравнения некоторому числу. Какова основная идея F-теста на улучшение качества оценивания. Приведите пример построения регрессии с ограничениями. Как формулируется гипотеза о наличие линейных ограничений на коэффициенты. Как провести тест Вальда. Для чего нужен тест Чоу.
Вопросы для самопроверки Как проверить значимость регрессии в целом. В чем заключается содержательный смысл гипотезы о равенстве коэффициента уравнения нулю. Как провести односторонний тест на равенство коэффициента нулю. В чем смысл доверительного интервала коэффициента. Как проверить гипотезу о равенстве коэффициента уравнения нулю при помощи доверительного интервала.. Как связаны между собой F и t статистика в парной модели. Как проверить гипотезу о равенстве коэффициента уравнения некоторому числу. Какова основная идея F-теста на улучшение качества оценивания. Приведите пример построения регрессии с ограничениями. Как формулируется гипотеза о наличие линейных ограничений на коэффициенты. Как провести тест Вальда. Для чего нужен тест Чоу.
 Тема 8. Мультиколлинеарность
Тема 8. Мультиколлинеарность
 Содержание лекции Понятие мультиколлинеарности Последствия мультиколлинеарности Обнаружение мультиколлинерности Коррекция мультиколлинеарности
Содержание лекции Понятие мультиколлинеарности Последствия мультиколлинеарности Обнаружение мультиколлинерности Коррекция мультиколлинеарности
 Полная мультиколлинеарность Коэффициенты по методу наименьших квадратов существуют не всегда, а только в том случае, когда определитель матрицы (X’X) отличен от нуля. Определитель будет равен нулю в случае, если столбцы матрицы X линейно зависимы. Такое может произойти, если между независимыми переменными существует точное линейное соотношение.
Полная мультиколлинеарность Коэффициенты по методу наименьших квадратов существуют не всегда, а только в том случае, когда определитель матрицы (X’X) отличен от нуля. Определитель будет равен нулю в случае, если столбцы матрицы X линейно зависимы. Такое может произойти, если между независимыми переменными существует точное линейное соотношение.
 Пример где Y - средняя оценка на экзамене состоящую из трех объясняющих переменных: I доход родителей, D среднее число часов, затраченных на обучение в день, W среднее число часов, затраченных на обучение в неделю. Очевидно, что W=7D.
Пример где Y - средняя оценка на экзамене состоящую из трех объясняющих переменных: I доход родителей, D среднее число часов, затраченных на обучение в день, W среднее число часов, затраченных на обучение в неделю. Очевидно, что W=7D.
 Устранение полной мультиколлинеарности Случай полной мультиколлинеарности отследить легко, поскольку в этом случае невозможно построить оценки по методу наименьших квадратов. Если в модели присутствует полная мультиколлинеарность, следует удалить из регрессионного уравнения одну из переменных, которые входят в линейное соотношение.
Устранение полной мультиколлинеарности Случай полной мультиколлинеарности отследить легко, поскольку в этом случае невозможно построить оценки по методу наименьших квадратов. Если в модели присутствует полная мультиколлинеарность, следует удалить из регрессионного уравнения одну из переменных, которые входят в линейное соотношение.
 Мультиколлинеарность Мультиколлинеарность – это проблема, когда тесная корреляционная зависимость между регрессорами ведет к получению ненадежных оценок регрессии
Мультиколлинеарность Мультиколлинеарность – это проблема, когда тесная корреляционная зависимость между регрессорами ведет к получению ненадежных оценок регрессии
 Неизбежность мультиколлинеарности Мультиколлинеарность – нормальное явление. Практически любая модель содержит мультиколлинеарность. Мы не обращаем внимания на мультиколлинеарность до появления явных симптомов. Только чрезмерно сильные связи становятся помехой.
Неизбежность мультиколлинеарности Мультиколлинеарность – нормальное явление. Практически любая модель содержит мультиколлинеарность. Мы не обращаем внимания на мультиколлинеарность до появления явных симптомов. Только чрезмерно сильные связи становятся помехой.
 Механизм действия мультиколлинеарности Мультиколлинеарность проявляется в совместном действии факторов: Построить модель – значит определить вклад каждого фактора. Если два или более фактора изменяются только совместно, их вклад по отдельности становится невозможно различить. Чем более сильно коррелированы переменные, тем труднее различить их вклад.
Механизм действия мультиколлинеарности Мультиколлинеарность проявляется в совместном действии факторов: Построить модель – значит определить вклад каждого фактора. Если два или более фактора изменяются только совместно, их вклад по отдельности становится невозможно различить. Чем более сильно коррелированы переменные, тем труднее различить их вклад.
 Зависимость мультиколлинеарности от выборки Мультиколлинеарность – явление, проявляющееся на уровне выборки: В одной выборке мультиколлинеарность может быть сильной, в другой слабой. Выборочные данные следует предварительно всесторонне исследовать. Полезен расчет выборочных коэффициентов корреляции, ковариационной матрицы и ее определителя.
Зависимость мультиколлинеарности от выборки Мультиколлинеарность – явление, проявляющееся на уровне выборки: В одной выборке мультиколлинеарность может быть сильной, в другой слабой. Выборочные данные следует предварительно всесторонне исследовать. Полезен расчет выборочных коэффициентов корреляции, ковариационной матрицы и ее определителя.
 Последствия мультиколлинеарности Поскольку матрица (X'X) близка к вырожденной и det(X'X) 0, то 1) на главной диагонали обратной матрицы стоят очень большие числа. Следовательно, теоретическая дисперсия i-го коэффициента достаточно большая и оценка дисперсии так же большая, следовательно, t - статистики небольшие, что может привести к статистической незначимости i-го коэффициента. Т. е. переменная оказывает значимое влияние на объясняемую переменную, а мы делаем вывод о ее незначимости.
Последствия мультиколлинеарности Поскольку матрица (X'X) близка к вырожденной и det(X'X) 0, то 1) на главной диагонали обратной матрицы стоят очень большие числа. Следовательно, теоретическая дисперсия i-го коэффициента достаточно большая и оценка дисперсии так же большая, следовательно, t - статистики небольшие, что может привести к статистической незначимости i-го коэффициента. Т. е. переменная оказывает значимое влияние на объясняемую переменную, а мы делаем вывод о ее незначимости.
 Последствия мультиколлинеарности (продолжение) 2) неустойчивость результатов оценивания: если мы добавим или уберем одно-два наблюдения, добавив или убрав, таким образом, одну-две строки к матрице X'X, то значения статистических оценок могут измениться существенным образом
Последствия мультиколлинеарности (продолжение) 2) неустойчивость результатов оценивания: если мы добавим или уберем одно-два наблюдения, добавив или убрав, таким образом, одну-две строки к матрице X'X, то значения статистических оценок могут измениться существенным образом
 Последствия мультиколлинеарности (продолжение) 3) Трудность интерпретации уравнения регрессии: разграничить влияние на переменную Y каждой переменной в отдельности уже не представляется возможным
Последствия мультиколлинеарности (продолжение) 3) Трудность интерпретации уравнения регрессии: разграничить влияние на переменную Y каждой переменной в отдельности уже не представляется возможным
 Обнаружение мультиколлинерности Анализ матрицы парных коэффициентов корреляции между регрессорами и если значение коэффициента корреляции близко к 1, то это считается признаком мультиколлинеарности. Расчет коэффициентов частной корреляции или расчет коэффициентов детерминации каждой из объясняющих переменных по всем другим объясняющим переменным в регрессии
Обнаружение мультиколлинерности Анализ матрицы парных коэффициентов корреляции между регрессорами и если значение коэффициента корреляции близко к 1, то это считается признаком мультиколлинеарности. Расчет коэффициентов частной корреляции или расчет коэффициентов детерминации каждой из объясняющих переменных по всем другим объясняющим переменным в регрессии
 Расчет определителя матрицы (Х’X) и если он близок к нулю, то это свидетельствует о наличии мультиколлинеарности. (Х’X) – симметричная положительно определенная матрица, следовательно, все ее собственные числа неотрицательны. Если определитель матрицы (Х’X) равен нулю, то минимальное собственное число так же ноль и непрерывность сохраняется. Следовательно, по значению манимального собственного числа можно судить и о близости к нулю определителя матрицы (Х’X). Обнаружение мультиколлинерности (продолжение)
Расчет определителя матрицы (Х’X) и если он близок к нулю, то это свидетельствует о наличии мультиколлинеарности. (Х’X) – симметричная положительно определенная матрица, следовательно, все ее собственные числа неотрицательны. Если определитель матрицы (Х’X) равен нулю, то минимальное собственное число так же ноль и непрерывность сохраняется. Следовательно, по значению манимального собственного числа можно судить и о близости к нулю определителя матрицы (Х’X). Обнаружение мультиколлинерности (продолжение)
 Обнаружение мультиколлинерности (продолжение) Внешние признаки, являющимся следствиями мультиколлинеарности: некоторые из оценок имеют неправильные с точки зрения экономической теории знаки или неоправданно большие значения; небольшое изменение исходных экономических данных приводит к существенному изменению оценок коэффициентов модели; большинство t-статистик коэффициентов малы, в то же время модель в целом является значимой, о чем говорит высокое значение F-статистики.
Обнаружение мультиколлинерности (продолжение) Внешние признаки, являющимся следствиями мультиколлинеарности: некоторые из оценок имеют неправильные с точки зрения экономической теории знаки или неоправданно большие значения; небольшое изменение исходных экономических данных приводит к существенному изменению оценок коэффициентов модели; большинство t-статистик коэффициентов малы, в то же время модель в целом является значимой, о чем говорит высокое значение F-статистики.
 Коррекция мультиколлинеарности Использование факторного анализа. Переход от исходного набора регрессоров, среди которых есть статистически зависимые, к новым регрессорам Z1,…,Zm при помощи метода главных компонент – вместо исходных переменных рассматриваем некоторые их линейные комбинации, корреляция между которыми мала или отсутствует вообще. Задача здесь – дать содержательную интерпретацию новым переменным Z. Если не удалось – возвращаемся к исходным переменным, используя обратные преобразования. Полученные оценки будут смещенными, но будут иметь меньшую дисперсию.
Коррекция мультиколлинеарности Использование факторного анализа. Переход от исходного набора регрессоров, среди которых есть статистически зависимые, к новым регрессорам Z1,…,Zm при помощи метода главных компонент – вместо исходных переменных рассматриваем некоторые их линейные комбинации, корреляция между которыми мала или отсутствует вообще. Задача здесь – дать содержательную интерпретацию новым переменным Z. Если не удалось – возвращаемся к исходным переменным, используя обратные преобразования. Полученные оценки будут смещенными, но будут иметь меньшую дисперсию.
 Коррекция мультиколлинеарности (продолжение) Среди всех имеющихся переменных отобрать наиболее существенно влияющих на объясняемую переменную факторов. Процедуры отбора будут рассмотрены ниже. Переход к смещенным методам оценивания.
Коррекция мультиколлинеарности (продолжение) Среди всех имеющихся переменных отобрать наиболее существенно влияющих на объясняемую переменную факторов. Процедуры отбора будут рассмотрены ниже. Переход к смещенным методам оценивания.
 Вопросы для самопроверки В каком случае возникает проблема мультиколлиенарности. Какие последствия для статистических выводов присутствие в модели мультиколлинеарности. Какие вы знаете статистические тесты, обнаруживающие мультиколлинеарность. Какие внешние признаки мультиколлинеарности. Как обнаружить наличие мультиколлинеарности в модели. Что делать, если в модели присутсвует мультиколлинеарность
Вопросы для самопроверки В каком случае возникает проблема мультиколлиенарности. Какие последствия для статистических выводов присутствие в модели мультиколлинеарности. Какие вы знаете статистические тесты, обнаруживающие мультиколлинеарность. Какие внешние признаки мультиколлинеарности. Как обнаружить наличие мультиколлинеарности в модели. Что делать, если в модели присутсвует мультиколлинеарность
 Тема 9. Ошибки спецификации
Тема 9. Ошибки спецификации
 Содержание лекции Невключение в модель существенных переменных Включение в модель несущественных переменных Неправильный выбор регрессионной функции
Содержание лекции Невключение в модель существенных переменных Включение в модель несущественных переменных Неправильный выбор регрессионной функции
 Невключение в модель существенных переменных - истинная модель - оцениваем оценка смещена
Невключение в модель существенных переменных - истинная модель - оцениваем оценка смещена
 Проблема смещения Оценка в короткой регрессии будет завышать или занижать истинное значение коэффициента в зависимости от знака смещения Оценка будет несмещенной в двух случаях: = 0 (Y действительно не зависит от Z); X и Z статистически независимы.
Проблема смещения Оценка в короткой регрессии будет завышать или занижать истинное значение коэффициента в зависимости от знака смещения Оценка будет несмещенной в двух случаях: = 0 (Y действительно не зависит от Z); X и Z статистически независимы.
 Иллюстрация смещения Предположим, что и положительны, а X и Z положительно коррелированны, тогда с увеличением X Y будет иметь тенденцию к росту, поскольку положителен; Z будет иметь тенденцию к увеличению, поскольку X и Z положительно коррелированны; Y получит дополнительное ускорение из-за увеличения Z, поскольку положительно. Изменение Y будет преувеличивать влияние текущих значений X, т. к. отчасти они будут связаны с изменениями Z. Т.е. часть изменения Y за счет изменения Z будет приписано X.
Иллюстрация смещения Предположим, что и положительны, а X и Z положительно коррелированны, тогда с увеличением X Y будет иметь тенденцию к росту, поскольку положителен; Z будет иметь тенденцию к увеличению, поскольку X и Z положительно коррелированны; Y получит дополнительное ускорение из-за увеличения Z, поскольку положительно. Изменение Y будет преувеличивать влияние текущих значений X, т. к. отчасти они будут связаны с изменениями Z. Т.е. часть изменения Y за счет изменения Z будет приписано X.
 Другие последствия т. е. - смещенная оценка, но обладающая меньшей дисперсией; оценка s2 смещена. Поскольку s2 участвует во многих статистических тестах, то используя их для проверки гипотез, мы можем получить ложные выводы.
Другие последствия т. е. - смещенная оценка, но обладающая меньшей дисперсией; оценка s2 смещена. Поскольку s2 участвует во многих статистических тестах, то используя их для проверки гипотез, мы можем получить ложные выводы.
 Включение в модель несущественных переменных - оцениваем - истинная модель точность оценки ухудшается
Включение в модель несущественных переменных - оцениваем - истинная модель точность оценки ухудшается
 Последствия включения в модель несущественной переменнй s2 и оценка несмещенные Дисперсия оценки в «длинной» регрессии больше, чем дисперсия оценки коэффициента при Х в истинной модели, поскольку мы вынуждены по тем же самым наблюдениям оценивать два параметра вместо одного. Потеря эффективности не случится, если переменные Х и Z некоррелированны. Потеря эффективности приводит к тому, что мы с большей трудностью отвергаем гипотезу о незначимости коэффициента, тем не менее оценка дисперсии останется несмещенной
Последствия включения в модель несущественной переменнй s2 и оценка несмещенные Дисперсия оценки в «длинной» регрессии больше, чем дисперсия оценки коэффициента при Х в истинной модели, поскольку мы вынуждены по тем же самым наблюдениям оценивать два параметра вместо одного. Потеря эффективности не случится, если переменные Х и Z некоррелированны. Потеря эффективности приводит к тому, что мы с большей трудностью отвергаем гипотезу о незначимости коэффициента, тем не менее оценка дисперсии останется несмещенной
 Невключение в модель существенных переменных - истинная модель - оцениваем ситуация является частным случаем ситуации с пропущенными переменными
Невключение в модель существенных переменных - истинная модель - оцениваем ситуация является частным случаем ситуации с пропущенными переменными
 Вопросы для самопроверки Какие вы знаете ошибки спецификации. Каковы последствия невключения в модель существенной переменной. Каковы последствия включения в модель несущественной перемнной. Каковы последствия выбора неправильной формы зависимости. Какой подход к построению модели теоретически более правильный : «снизу вверх» или «сверху вниз»
Вопросы для самопроверки Какие вы знаете ошибки спецификации. Каковы последствия невключения в модель существенной переменной. Каковы последствия включения в модель несущественной перемнной. Каковы последствия выбора неправильной формы зависимости. Какой подход к построению модели теоретически более правильный : «снизу вверх» или «сверху вниз»
 Тема 10. Процедуры отбора объясняющих переменных
Тема 10. Процедуры отбора объясняющих переменных
 Темы лекций Две точки зрения на оценку уравнения регрессии, получаемого после отбора наиболее существенных предсказывающих переменных «Все воэможные регрессии» Процедура пошагового присоединения переменных
Темы лекций Две точки зрения на оценку уравнения регрессии, получаемого после отбора наиболее существенных предсказывающих переменных «Все воэможные регрессии» Процедура пошагового присоединения переменных
 Две точки зрения Модель регрессии является истинной, тогда при помощи метода наименьших квадратов получается несмещенная и эффективная оценка коэффициентов регрессии. Тогда принудительное приравнивание части коэффициентов к нулю, приводитк смещенным оценкам коэффициентов при оставшихся переменных. Процесс отбора существенных переменных можно рассматривать как процесс выбора истинной модели из множества возможных линейных моделей, которые могут быть построены с помощью набора объясняющих переменных, и тогда полученные после отбора оценки коэффициентов можно рассматривать как несмещенные (преобладающая).
Две точки зрения Модель регрессии является истинной, тогда при помощи метода наименьших квадратов получается несмещенная и эффективная оценка коэффициентов регрессии. Тогда принудительное приравнивание части коэффициентов к нулю, приводитк смещенным оценкам коэффициентов при оставшихся переменных. Процесс отбора существенных переменных можно рассматривать как процесс выбора истинной модели из множества возможных линейных моделей, которые могут быть построены с помощью набора объясняющих переменных, и тогда полученные после отбора оценки коэффициентов можно рассматривать как несмещенные (преобладающая).
 Если X-ы случайны Для случая, когда объясняющие переменные – случайные величины, вопрос о правильности (истинности) модели не стоит. Все, что мы ищем в этом случае – модель, сохраняющую ошибку предсказания на разумном уровне при ограниченном количестве переменных.
Если X-ы случайны Для случая, когда объясняющие переменные – случайные величины, вопрос о правильности (истинности) модели не стоит. Все, что мы ищем в этом случае – модель, сохраняющую ошибку предсказания на разумном уровне при ограниченном количестве переменных.
 «Все возможные регрессии» Проведем р парных регрессий Y на X1,…Xp и выберем ту переменную, для которой коэффициент детерминации наибольший - . на этом шаге мы найдем одну объясняющую переменную, которую можно назвать наиболее информативной объясняющей переменной при условии, что в регрессионную модель мы можем включить только одну из имеющегося набора объясняющих переменных. Проведем р*(р-1) регрессий, каждый раз включая две из р переменных и выберем ту, которая дает наибольшее значение – пара (X(1), X(2)) – наиболее информативная пара переменных: эта пара будет иметь наиболее тесную статистическую связь с результирующим показателем Y. В состав этой пары переменная из первого шага может и не войти. Находим три наиболее информативных объясняющих переменных, проведя р*(р-1)*(р-2) регрессий -
«Все возможные регрессии» Проведем р парных регрессий Y на X1,…Xp и выберем ту переменную, для которой коэффициент детерминации наибольший - . на этом шаге мы найдем одну объясняющую переменную, которую можно назвать наиболее информативной объясняющей переменной при условии, что в регрессионную модель мы можем включить только одну из имеющегося набора объясняющих переменных. Проведем р*(р-1) регрессий, каждый раз включая две из р переменных и выберем ту, которая дает наибольшее значение – пара (X(1), X(2)) – наиболее информативная пара переменных: эта пара будет иметь наиболее тесную статистическую связь с результирующим показателем Y. В состав этой пары переменная из первого шага может и не войти. Находим три наиболее информативных объясняющих переменных, проведя р*(р-1)*(р-2) регрессий -
 Когда остановиться? Выбираем то k, для которого величина максимальна
Когда остановиться? Выбираем то k, для которого величина максимальна
 Что плохо? Очень много регрессий число регрессий, которые необходимо оценить, большое (равное 2р-2, для p = 20 число возможных переборов будет больше миллиона)
Что плохо? Очень много регрессий число регрессий, которые необходимо оценить, большое (равное 2р-2, для p = 20 число возможных переборов будет больше миллиона)
 Процедура пошагового присоединения переменных Среди имеющихся р переменных выбираем ту, для которой коэффициент корреляции с объясняемой переменной наибольший. Теперь мы перебираем не все возможные пары переменных, а лишь те, в которых участвует переменная, полученная на первом шаге. Число переборов в этом случае существенно уменьшится Среди оставшихся переменных выбираем ту, которая имеет с объясняемой переменной наибольший коэффициент частной корреляции, очищенный от влияния переменной, полученной на первом шаге.
Процедура пошагового присоединения переменных Среди имеющихся р переменных выбираем ту, для которой коэффициент корреляции с объясняемой переменной наибольший. Теперь мы перебираем не все возможные пары переменных, а лишь те, в которых участвует переменная, полученная на первом шаге. Число переборов в этом случае существенно уменьшится Среди оставшихся переменных выбираем ту, которая имеет с объясняемой переменной наибольший коэффициент частной корреляции, очищенный от влияния переменной, полученной на первом шаге.
 Число переборов Число переборов - для р = 20 число переборов будет 209.
Число переборов Число переборов - для р = 20 число переборов будет 209.
 Вопросы для самопроверки Для чего нужны процедуры отбора объясняющих переменных. Какого взгляда на такие процедуры вы придерживайтесь. Опишите процедуру «Все возможные регрессии». Каковы ее достоинства и недостатки. Опишите процедуру пошагового присоединения переменных. Каковы ее достоинства и недостатки.
Вопросы для самопроверки Для чего нужны процедуры отбора объясняющих переменных. Какого взгляда на такие процедуры вы придерживайтесь. Опишите процедуру «Все возможные регрессии». Каковы ее достоинства и недостатки. Опишите процедуру пошагового присоединения переменных. Каковы ее достоинства и недостатки.
 Тема 11. Обобщенный метод наименьших квадратов ОМНК
Тема 11. Обобщенный метод наименьших квадратов ОМНК
 Темы лекции Обобщенная линейная регрессионная модель Обобщенный метод наименьших квадратов Доступный обобщенный метод наименьших квадратов
Темы лекции Обобщенная линейная регрессионная модель Обобщенный метод наименьших квадратов Доступный обобщенный метод наименьших квадратов
 Обобщенная линейная регрессионная модель модель в матричной форме - матрица ковариаций Матрица предполагается положительно определенной
Обобщенная линейная регрессионная модель модель в матричной форме - матрица ковариаций Матрица предполагается положительно определенной
 КМЛРМ
КМЛРМ
 Гетероскедастичность
Гетероскедастичность
 Автокорреляция первого порядка
Автокорреляция первого порядка
 Применение МНК МНК-оценки несмещенные МНК-оценки коэффициентов неэффективны, т. е. не обладают наименьшей дисперсией из всех возможных линейных несмещенных оценок МНК-оценки дисперсий оценок коэффициентов смещены и несостоятельны Можно повысить эффективность оценок за счет дополнительной информации о матрице
Применение МНК МНК-оценки несмещенные МНК-оценки коэффициентов неэффективны, т. е. не обладают наименьшей дисперсией из всех возможных линейных несмещенных оценок МНК-оценки дисперсий оценок коэффициентов смещены и несостоятельны Можно повысить эффективность оценок за счет дополнительной информации о матрице
 Получение эффективных оценок Для любой положительно определенной матрицы существует невырожденная матрица Н такая, что Перепишем это равенство следующим образом: Откуда
Получение эффективных оценок Для любой положительно определенной матрицы существует невырожденная матрица Н такая, что Перепишем это равенство следующим образом: Откуда
 преобразуем исходную модель: или найдем матрицу ковариаций нового случайного члена: матрица ковариаций преобразованной модели удовлетворяет условиям Гаусса-Маркова. Поэтому, для оценки этой модели можно применять обычный метод наименьших квадратов: эта оценка является несмещенной и эффективной матрица ковариаций вектора
преобразуем исходную модель: или найдем матрицу ковариаций нового случайного члена: матрица ковариаций преобразованной модели удовлетворяет условиям Гаусса-Маркова. Поэтому, для оценки этой модели можно применять обычный метод наименьших квадратов: эта оценка является несмещенной и эффективной матрица ковариаций вектора
 Теорема Айткена В классе линейных несмещенных оценок коэффициентов уравнения оценка является эффективной, т. е. обладает наименьшей матрицей ковариаций
Теорема Айткена В классе линейных несмещенных оценок коэффициентов уравнения оценка является эффективной, т. е. обладает наименьшей матрицей ковариаций
 Проблема Для построения ОМНК-оценки нам необходимо знать матрицу МЫ ЕЕ НЕ ЗНАЕМ Поэтому матрицу тоже надо оценить Поскольку в этой матрице всего N(N-1)/2 элементов, то нет никакой надежды получить состоятельные)оценки, имея всего N наблюдений. Для получения состоятельной оценки матрицы необходимо наложить некоторые ограничения на ее структуру
Проблема Для построения ОМНК-оценки нам необходимо знать матрицу МЫ ЕЕ НЕ ЗНАЕМ Поэтому матрицу тоже надо оценить Поскольку в этой матрице всего N(N-1)/2 элементов, то нет никакой надежды получить состоятельные)оценки, имея всего N наблюдений. Для получения состоятельной оценки матрицы необходимо наложить некоторые ограничения на ее структуру
 Доступный обобщенный метод наименьших квадратов Пусть V – состоятельная оценка матрицы , тогда, подставляя ее, осуществляем Доступный обобщенный метод наименьших квадратов (feasible GLS), .
Доступный обобщенный метод наименьших квадратов Пусть V – состоятельная оценка матрицы , тогда, подставляя ее, осуществляем Доступный обобщенный метод наименьших квадратов (feasible GLS), .
 Свойства оценок по ДОМНК смещены состоятельны асимптотически эффективны так что ДОМНК-оценки ведут себя непредсказуемым образом на малых выборках, поэтому в некоторых ситуациях лучше использовать МНК-оценки с состоятельными стандартными ошибками
Свойства оценок по ДОМНК смещены состоятельны асимптотически эффективны так что ДОМНК-оценки ведут себя непредсказуемым образом на малых выборках, поэтому в некоторых ситуациях лучше использовать МНК-оценки с состоятельными стандартными ошибками
 Коэффициент детерминации Для обобщенной регрессионной модели нельзя использовать R2 в качестве удовлетворительной мерой качества подгонки. Он не обязательно лежит в интервале [0;1], а добавление или удаление регрессоров не обязательно влечет за собой его увеличение или уменьшение. Так же нет смысла рассматривать коэффициент детерминации и для вспомогательной регрессии, поскольку среди преобразованных регрессоров уже может и не быть константы; в общем случае трудно установить связь между качеством подгонки вспомогательной регрессии и исходной модели.
Коэффициент детерминации Для обобщенной регрессионной модели нельзя использовать R2 в качестве удовлетворительной мерой качества подгонки. Он не обязательно лежит в интервале [0;1], а добавление или удаление регрессоров не обязательно влечет за собой его увеличение или уменьшение. Так же нет смысла рассматривать коэффициент детерминации и для вспомогательной регрессии, поскольку среди преобразованных регрессоров уже может и не быть константы; в общем случае трудно установить связь между качеством подгонки вспомогательной регрессии и исходной модели.
 Вопросы для самопроверки Какая модель называется Обобщенной линейной регрессионной моделью. Как выглядит матрица ковариаций ошибок в случае КМЛРМ. Как выглядит матрица ковариаций ошибок в случае гетероскедастичности Как выглядит матрица ковариаций ошибок в случае автокорреляции первого порядка. Выведите формулу коэффициентов по обобщенному методу наименьших квадратов. Сформулируйте теорему Айткена. Как оценивать матрицу ковариаций ошибок. Что такое доступный обобщенный метод наименьших квадратов.
Вопросы для самопроверки Какая модель называется Обобщенной линейной регрессионной моделью. Как выглядит матрица ковариаций ошибок в случае КМЛРМ. Как выглядит матрица ковариаций ошибок в случае гетероскедастичности Как выглядит матрица ковариаций ошибок в случае автокорреляции первого порядка. Выведите формулу коэффициентов по обобщенному методу наименьших квадратов. Сформулируйте теорему Айткена. Как оценивать матрицу ковариаций ошибок. Что такое доступный обобщенный метод наименьших квадратов.
 Тема 12. Гетероскедастичность
Тема 12. Гетероскедастичность
 Темы лекции Природа проблемы гетероскедастичности Последствия гетероскедастичности Обнаружение гетероскедастичности Коррекция гетероскедастичности
Темы лекции Природа проблемы гетероскедастичности Последствия гетероскедастичности Обнаружение гетероскедастичности Коррекция гетероскедастичности
 Определение гетероскедастичности Гетероскедастичность – это неоднородность наблюдений. Она характеризуется тем, что не выполняется 4-е условие Гаусса-Маркова: .
Определение гетероскедастичности Гетероскедастичность – это неоднородность наблюдений. Она характеризуется тем, что не выполняется 4-е условие Гаусса-Маркова: .
 Иллюстрация определения гетероскедастичности
Иллюстрация определения гетероскедастичности
 Модели с гетероскедастичными остатками Причиной непостоянства дисперсии эконометрической модели часто является ее зависимость от масштаба рассматриваемых явлений. В модель ошибка входит как аддитивное слагаемое. В то же время часто она имеет относительный характер и определяется по отношению к измеренному уровню рассматриваемых факторов.
Модели с гетероскедастичными остатками Причиной непостоянства дисперсии эконометрической модели часто является ее зависимость от масштаба рассматриваемых явлений. В модель ошибка входит как аддитивное слагаемое. В то же время часто она имеет относительный характер и определяется по отношению к измеренному уровню рассматриваемых факторов.
 Пример модели с гетероскедастичным случайным членом y x
Пример модели с гетероскедастичным случайным членом y x
 Примеры моделей с гетероскедастичным случайным членом а) в) б) а) Дисперсия 2 растет по мере увеличения значений объясняющей переменной X б) Дисперсия 2 имеет наибольшие значения при средних значениях X, уменьшаясь по мере приближения к крайним значениям в) Дисперсия ошибки наибольшая при малых значениях X, быстро уменьшается и становится однородной по мере увеличения X
Примеры моделей с гетероскедастичным случайным членом а) в) б) а) Дисперсия 2 растет по мере увеличения значений объясняющей переменной X б) Дисперсия 2 имеет наибольшие значения при средних значениях X, уменьшаясь по мере приближения к крайним значениям в) Дисперсия ошибки наибольшая при малых значениях X, быстро уменьшается и становится однородной по мере увеличения X
 Перекрестные выборки Чаще гетероскедастичность возникает в моделях, основанных на перекрестных выборках, но встречаются и во временных рядах. Типичные «болезни»: Перекрестные выборки – гетероскедастичность Временные ряды – автокорреляция
Перекрестные выборки Чаще гетероскедастичность возникает в моделях, основанных на перекрестных выборках, но встречаются и во временных рядах. Типичные «болезни»: Перекрестные выборки – гетероскедастичность Временные ряды – автокорреляция
 Виды гетероскедастичности 1. Истинная гетероскедастичность Вызывается непостоянством дисперсии случайного члена, ее зависимостью от различных факторов. 2. Ложная гетероскедастичность Вызывается ошибочной спецификацией модели регрессии.
Виды гетероскедастичности 1. Истинная гетероскедастичность Вызывается непостоянством дисперсии случайного члена, ее зависимостью от различных факторов. 2. Ложная гетероскедастичность Вызывается ошибочной спецификацией модели регрессии.
 Источники гетероскедастичности Истинная гетероскедастичность возникает в перекрестных выборках при зависимости масштаба изменений зависимой переменной от некоторой переменной, называемой фактором пропорциональности (Z).
Источники гетероскедастичности Истинная гетероскедастичность возникает в перекрестных выборках при зависимости масштаба изменений зависимой переменной от некоторой переменной, называемой фактором пропорциональности (Z).
 Источники гетероскедастичности – 1 Наиболее распространенный случай истинной гетероскедастичности – 1: дисперсия растет с ростом одного из факторов.
Источники гетероскедастичности – 1 Наиболее распространенный случай истинной гетероскедастичности – 1: дисперсия растет с ростом одного из факторов.
 Источники гетероскедастичности Истинная гетероскедастичность возникает также и во временных рядах, когда зависимая переменная имеет большой интервал качественно неоднородных значений или высокий темп изменения (инфляция, технологические сдвиги, изменения в законодательстве, потребительские предпочтения и т.д.).
Источники гетероскедастичности Истинная гетероскедастичность возникает также и во временных рядах, когда зависимая переменная имеет большой интервал качественно неоднородных значений или высокий темп изменения (инфляция, технологические сдвиги, изменения в законодательстве, потребительские предпочтения и т.д.).
 Гетероскедастичность как следствие ошибки спецификации модели. Пример Если вместо истинной (гомоскедастичной) модели используется линейная модель , то дисперсия остатков линейной модели пропорциональна квадрату переменной Xj:
Гетероскедастичность как следствие ошибки спецификации модели. Пример Если вместо истинной (гомоскедастичной) модели используется линейная модель , то дисперсия остатков линейной модели пропорциональна квадрату переменной Xj:
 Гетероскедастичность простейшего вида Мы в дальнейшем будем рассматривать, главным образом, только гетероскедастичность простейшего вида:
Гетероскедастичность простейшего вида Мы в дальнейшем будем рассматривать, главным образом, только гетероскедастичность простейшего вида:
 Последствия гетероскедастичности 1. Истинная гетероскедастичность не приводит к смещению оценок коэффициентов регрессии 2. Стандартные ошибки коэффициентов (вычисленные в предположении. гомоскедастичности) будут занижены. Это приведет к завышению t-статистик и даст неправильное (завышенное) представление о точности оценок.
Последствия гетероскедастичности 1. Истинная гетероскедастичность не приводит к смещению оценок коэффициентов регрессии 2. Стандартные ошибки коэффициентов (вычисленные в предположении. гомоскедастичности) будут занижены. Это приведет к завышению t-статистик и даст неправильное (завышенное) представление о точности оценок.
 Обнаружение гетероскедастичности Обнаружение гетероскедастичности в каждом конкретном случае – довольно сложная задача. Для знания необходимо знать распределение случайной величины Y/X=xi . На практике часто для каждого конкретного значения xi известно лишь одно yi, что не позволяет оценить дисперсию случайной величины Y/X=xi.
Обнаружение гетероскедастичности Обнаружение гетероскедастичности в каждом конкретном случае – довольно сложная задача. Для знания необходимо знать распределение случайной величины Y/X=xi . На практике часто для каждого конкретного значения xi известно лишь одно yi, что не позволяет оценить дисперсию случайной величины Y/X=xi.
 Обнаружение гетероскедастичности Предварительная работа: 1. Нет ли очевидных ошибок спецификации? 2. Можно ли содержательно предполагать какой-то вид гетероскедастичности? 3. Рассмотрение графиков остатков:
Обнаружение гетероскедастичности Предварительная работа: 1. Нет ли очевидных ошибок спецификации? 2. Можно ли содержательно предполагать какой-то вид гетероскедастичности? 3. Рассмотрение графиков остатков:
 Обнаружение гетероскедастичности Тесты: 1. Тест ранговой корреляции Спирмена. 2. Тест Парка. 3. Тест Глейзера. 4. Тест Голдфелда-Квандта. 5. Тест Уайта. 6. Тест Бреуша-Пагана.
Обнаружение гетероскедастичности Тесты: 1. Тест ранговой корреляции Спирмена. 2. Тест Парка. 3. Тест Глейзера. 4. Тест Голдфелда-Квандта. 5. Тест Уайта. 6. Тест Бреуша-Пагана.
 Тест Глейзера Здесь предполагается, что дисперсии связаны с фактором пропорциональности Z в виде: Т.к. средние квадратические отклонения неизвестны, то их заменяют модулями оценок отклонений .
Тест Глейзера Здесь предполагается, что дисперсии связаны с фактором пропорциональности Z в виде: Т.к. средние квадратические отклонения неизвестны, то их заменяют модулями оценок отклонений .
 Тест Глейзера. Алгоритм применения 1. Строится уравнение регрессии: и вычисляются остатки . 2. Выбирается фактор пропорциональности Z и оценивают вспомогательное уравнение регрессии: Изменяя , строят несколько моделей: 3. Статистическая значимость коэффициента 1 в каждом случае означает наличие гетероскедастичности. 4. Если для нескольких моделей будет получена значимая оценка 1 , то характер гетероскедастичности определяют по наиболее значимой из них.
Тест Глейзера. Алгоритм применения 1. Строится уравнение регрессии: и вычисляются остатки . 2. Выбирается фактор пропорциональности Z и оценивают вспомогательное уравнение регрессии: Изменяя , строят несколько моделей: 3. Статистическая значимость коэффициента 1 в каждом случае означает наличие гетероскедастичности. 4. Если для нескольких моделей будет получена значимая оценка 1 , то характер гетероскедастичности определяют по наиболее значимой из них.
 Тесты Парка и Глейзера. Выводы Отметим, что как в тесте Парка, так и в тесте Глейзера для отклонений i может нарушаться условие гомоскедастичности. Однако, во многих случаях используемые в тестах модели являются достаточно хорошими для определения гетероскедастичности.
Тесты Парка и Глейзера. Выводы Отметим, что как в тесте Парка, так и в тесте Глейзера для отклонений i может нарушаться условие гомоскедастичности. Однако, во многих случаях используемые в тестах модели являются достаточно хорошими для определения гетероскедастичности.
 Тест Голдфелда-Квандта В этом тесте предполагается: 1. Стандартные отклонения остатков пропорциональны фактору пропорциональности Z, т.е. 2. Случайный член имеет нормальное распределение и отсутствует автокорреляция остатков (предпосылка 30).
Тест Голдфелда-Квандта В этом тесте предполагается: 1. Стандартные отклонения остатков пропорциональны фактору пропорциональности Z, т.е. 2. Случайный член имеет нормальное распределение и отсутствует автокорреляция остатков (предпосылка 30).
 Тест Голдфелда-Квандта. Алгоритм применения 1. Выделяют фактор пропорциональности Z = Xk. Данные упорядочиваются в порядке возрастания величины Z. 2. Отбрасывают среднюю треть упорядоченных наблюдений. Для первой и последней третей строятся две отдельные регрессии, используя ту же спецификацию модели регрессии. 3. Количество наблюдений в этих подвыборках должно быть одинаково. Обозначим его l.
Тест Голдфелда-Квандта. Алгоритм применения 1. Выделяют фактор пропорциональности Z = Xk. Данные упорядочиваются в порядке возрастания величины Z. 2. Отбрасывают среднюю треть упорядоченных наблюдений. Для первой и последней третей строятся две отдельные регрессии, используя ту же спецификацию модели регрессии. 3. Количество наблюдений в этих подвыборках должно быть одинаково. Обозначим его l.
 Тест Голдфелда-Квандта. Алгоритм применения 4. Берутся суммы квадратов остатков для регрессий по первой трети RSS1 и последней трети RSS3. Рассчитывают их отношение: 5. Используем F-тест для проверки гомоскедастичности. Если статистика GQ удовлетворяет неравенству то гипотеза гомоскедастичности остатков отвергается на уровне значимости .
Тест Голдфелда-Квандта. Алгоритм применения 4. Берутся суммы квадратов остатков для регрессий по первой трети RSS1 и последней трети RSS3. Рассчитывают их отношение: 5. Используем F-тест для проверки гомоскедастичности. Если статистика GQ удовлетворяет неравенству то гипотеза гомоскедастичности остатков отвергается на уровне значимости .
 Тест Голдфелда-Квандта. Замечание Тест Голдфелда-Квандта применим и для случая обратной пропорциональности: При этом используется та же процедура, но тестовая статистика равна:
Тест Голдфелда-Квандта. Замечание Тест Голдфелда-Квандта применим и для случая обратной пропорциональности: При этом используется та же процедура, но тестовая статистика равна:
 Тест Уайта Предполагается, что дисперсии связаны с объясняющими переменными в виде: где f() – квадратичная функция от аргументов. Т.к. дисперсии неизвестны, то их заменяют оценками квадратов отклонений ei2.
Тест Уайта Предполагается, что дисперсии связаны с объясняющими переменными в виде: где f() – квадратичная функция от аргументов. Т.к. дисперсии неизвестны, то их заменяют оценками квадратов отклонений ei2.
 Тест Уайта. Алгоритм применения (на примере трех переменных) 1. Строится уравнение регрессии: и вычисляются остатки . 2. Оценивают вспомогательное уравнение регрессии:
Тест Уайта. Алгоритм применения (на примере трех переменных) 1. Строится уравнение регрессии: и вычисляются остатки . 2. Оценивают вспомогательное уравнение регрессии:
 Тест Уайта. Алгоритм применения (на примере трех переменных) 3. Определяют из вспомогательного уравнения тестовую статистику 4. Проверяют общую значимость уравнения с помощью критерия 2. Если то гипотеза гомоскедастичности отвергается. Число степеней свободы k равно числу объясняющих Переменных вспомогательного уравнения. В частности, Для рассматриваемого случая k = 9.
Тест Уайта. Алгоритм применения (на примере трех переменных) 3. Определяют из вспомогательного уравнения тестовую статистику 4. Проверяют общую значимость уравнения с помощью критерия 2. Если то гипотеза гомоскедастичности отвергается. Число степеней свободы k равно числу объясняющих Переменных вспомогательного уравнения. В частности, Для рассматриваемого случая k = 9.
 Тест Уайта. Замечания Тест Уайта является более общим чем тест Голдфелда-Квандта. Неудобство использования теста Уайта: Если отвергается нулевая гипотеза о наличии гомоскедастичности то неясно, что делать дальше.
Тест Уайта. Замечания Тест Уайта является более общим чем тест Голдфелда-Квандта. Неудобство использования теста Уайта: Если отвергается нулевая гипотеза о наличии гомоскедастичности то неясно, что делать дальше.
 Средства при гетероскедастичности 1. Использовать обобщенный метод наименьших квадратов. 2. Переопределить переменные. 3. Вычисление стандартных ошибок с поправкой на гетероскедастичность (метод Уайта).
Средства при гетероскедастичности 1. Использовать обобщенный метод наименьших квадратов. 2. Переопределить переменные. 3. Вычисление стандартных ошибок с поправкой на гетероскедастичность (метод Уайта).
 Обобщенный метод наименьших квадратов При нарушении гомоскедастичности и наличии автокорреляции остатков рекомендуется вместо традиционного МНК использовать обобщенный МНК. Его для случая устранения гетероскедастичности часто называют методом взвешенных наименьших квадратов. Основан на делении каждого наблюдаемого значения на соответствующее ему стандартное отклонение остатков. Метод применим, если известны дисперсии для каждого наблюдения.
Обобщенный метод наименьших квадратов При нарушении гомоскедастичности и наличии автокорреляции остатков рекомендуется вместо традиционного МНК использовать обобщенный МНК. Его для случая устранения гетероскедастичности часто называют методом взвешенных наименьших квадратов. Основан на делении каждого наблюдаемого значения на соответствующее ему стандартное отклонение остатков. Метод применим, если известны дисперсии для каждого наблюдения.
 Метод взвешенных наименьших квадратов. Случай парной регрессии Получили уравнение регрессии без свободного члена, но с дополнительной объясняющей переменной Z и с «преобразованным» остатком . Можно показать, что для него выполняются условия Гаусса-Маркова 1 – 5.
Метод взвешенных наименьших квадратов. Случай парной регрессии Получили уравнение регрессии без свободного члена, но с дополнительной объясняющей переменной Z и с «преобразованным» остатком . Можно показать, что для него выполняются условия Гаусса-Маркова 1 – 5.
 Метод взвешенных наименьших квадратов. Случай парной регрессии На практике, значения дисперсии остатков, как правило, не известны. Для применения метода ВНК необходимо сделать реалистичные предположения об этих значениях. Например: Дисперсии пропорциональны Xi: Дисперсии пропорциональны Xi2:
Метод взвешенных наименьших квадратов. Случай парной регрессии На практике, значения дисперсии остатков, как правило, не известны. Для применения метода ВНК необходимо сделать реалистичные предположения об этих значениях. Например: Дисперсии пропорциональны Xi: Дисперсии пропорциональны Xi2:
 Вопросы для самопроверки Что такое гетеровскедастичность Из-за чего может возникнуть гетеровскедастичность в модели. Какие последствия наличия гетеровскедастичности в модели. Как выглядит матрица ковариаций ошибок в случае наличия гетеровскедастичности Какие вы знаете еще тесты для обнаружения гетеровскедастичности. Какова основная идея теста Уайта. Что делать, если тест Уайта обнаружил гетероскедастичность. Как обнаружить гетеровскедастичность графически. Как корректировать модель при наличии гетеровскедастичность. Что такое взвешенный метод наименьших квадратов. Как осуществить двухшаговую процедуру коррекции гетероскедастичности.
Вопросы для самопроверки Что такое гетеровскедастичность Из-за чего может возникнуть гетеровскедастичность в модели. Какие последствия наличия гетеровскедастичности в модели. Как выглядит матрица ковариаций ошибок в случае наличия гетеровскедастичности Какие вы знаете еще тесты для обнаружения гетеровскедастичности. Какова основная идея теста Уайта. Что делать, если тест Уайта обнаружил гетероскедастичность. Как обнаружить гетеровскедастичность графически. Как корректировать модель при наличии гетеровскедастичность. Что такое взвешенный метод наименьших квадратов. Как осуществить двухшаговую процедуру коррекции гетероскедастичности.
 Тема 13. Автокорреляция
Тема 13. Автокорреляция
 Темы лекции Природа проблемы автокорреляции остатков. Последствия автокорреляции. Обнаружения автокорреляции. Коррекция автокорреляции.
Темы лекции Природа проблемы автокорреляции остатков. Последствия автокорреляции. Обнаружения автокорреляции. Коррекция автокорреляции.
 Определение автокорреляции Автокорреляция (последовательная корреляция) – это корреляция между наблюдаемыми показателями во времени (временные ряды) или в пространстве (перекрестные данные). Автокорреляция остатков характеризуется тем, что не выполняется 5 условие Гаусса-Маркова:
Определение автокорреляции Автокорреляция (последовательная корреляция) – это корреляция между наблюдаемыми показателями во времени (временные ряды) или в пространстве (перекрестные данные). Автокорреляция остатков характеризуется тем, что не выполняется 5 условие Гаусса-Маркова:
 Виды автокорреляции
Виды автокорреляции
 Причины чистой автокорреляции 1. Инерция. Трансформация, изменение многих экономических показателей обладает инерционностью. 2. Эффект паутины. Многие экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом) 3. Сглаживание данных. Усреднение данных по некоторому продолжительному интервалу времени.
Причины чистой автокорреляции 1. Инерция. Трансформация, изменение многих экономических показателей обладает инерционностью. 2. Эффект паутины. Многие экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом) 3. Сглаживание данных. Усреднение данных по некоторому продолжительному интервалу времени.
 Автокорреляция первого порядка случайный член рассматриваемого уравнения регрессии, коэффициент автокорреляции первого порядка, случайный член, не подверженный автокорреляции
Автокорреляция первого порядка случайный член рассматриваемого уравнения регрессии, коэффициент автокорреляции первого порядка, случайный член, не подверженный автокорреляции
 Сезонная автокорреляция случайный член рассматриваемого уравнения регрессии, коэффициент сезонной автокорреляции, случайный член, не подверженный автокорреляции
Сезонная автокорреляция случайный член рассматриваемого уравнения регрессии, коэффициент сезонной автокорреляции, случайный член, не подверженный автокорреляции
 Автокорреляция второго порядка случайный член рассматриваемого уравнения регрессии, 1, 2 коэффициенты автокорреляции первого порядка, случайный член, не подверженный автокорреляции
Автокорреляция второго порядка случайный член рассматриваемого уравнения регрессии, 1, 2 коэффициенты автокорреляции первого порядка, случайный член, не подверженный автокорреляции
 Классический случайный член (автокорреляция отсутствует)
Классический случайный член (автокорреляция отсутствует)
 Положительная автокорреляция Положительная автокорреляция – наиболее важный для экономики случай
Положительная автокорреляция Положительная автокорреляция – наиболее важный для экономики случай
 Отрицательная автокорреляция
Отрицательная автокорреляция
 Пример влияния автокорреляции на случайную выборку Рассмотрим выборку из 50 независимых нормально распределенных с нулевым средним значений i. С целью ознакомления с влиянием автокорреляции будем вводить в нее положительную, а затем отрицательную автокорреляцию.
Пример влияния автокорреляции на случайную выборку Рассмотрим выборку из 50 независимых нормально распределенных с нулевым средним значений i. С целью ознакомления с влиянием автокорреляции будем вводить в нее положительную, а затем отрицательную автокорреляцию.
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Пример влияния автокорреляции на случайную выборку
Пример влияния автокорреляции на случайную выборку
 Ложная автокорреляция (автокорреляция, вызванная ошибочной спецификацией) X2 сама является автокоррелированной переменной, Значение мало по сравнению с величиной
Ложная автокорреляция (автокорреляция, вызванная ошибочной спецификацией) X2 сама является автокоррелированной переменной, Значение мало по сравнению с величиной
 Ложная автокорреляция как результат неправильного выбора функциональной формы
Ложная автокорреляция как результат неправильного выбора функциональной формы
 Последствия автокорреляции 1. Истинная автокорреляция не приводит к смещению оценок регрессии, но оценки перестают быть эффективными. 2. Автокорреляция (особенно положительная) часто приводит к уменьшению стандартных ошибок коэффициентов, что влечет за собой увеличение t-статистик. 3. Оценка дисперсии остатков Se2 является смещенной оценкой истинного значения e2 , во многих случаях занижая его. 4. В силу вышесказанного выводы по оценке качества коэффициентов и модели в целом, возможно, будут неверными. Это приводит к ухудшению прогнозных качеств модели.
Последствия автокорреляции 1. Истинная автокорреляция не приводит к смещению оценок регрессии, но оценки перестают быть эффективными. 2. Автокорреляция (особенно положительная) часто приводит к уменьшению стандартных ошибок коэффициентов, что влечет за собой увеличение t-статистик. 3. Оценка дисперсии остатков Se2 является смещенной оценкой истинного значения e2 , во многих случаях занижая его. 4. В силу вышесказанного выводы по оценке качества коэффициентов и модели в целом, возможно, будут неверными. Это приводит к ухудшению прогнозных качеств модели.
 Обнаружение автокорреляции 1. Графический метод. 2. Метод рядов. 3. Специальные тесты.
Обнаружение автокорреляции 1. Графический метод. 2. Метод рядов. 3. Специальные тесты.
 Обнаружение автокорреляции. Тест Дарбина-Уотсона Критерий Дарбина-Уотсона предназначен для обнаружения автокорреляции первого порядка. Он основан на анализе остатков уравнения регрессии.
Обнаружение автокорреляции. Тест Дарбина-Уотсона Критерий Дарбина-Уотсона предназначен для обнаружения автокорреляции первого порядка. Он основан на анализе остатков уравнения регрессии.
 Тест Дарбина-Уотсона. Ограничения Ограничения: 1. Тест не предназначен для обнаружения других видов автокорреляции (более чем первого) и не обнаруживает ее. 2. В модели должен присутствовать свободный член. 3. Данные должны иметь одинаковую периодичность (не должно быть пропусков в наблюдениях). 4. Тест не применим к авторегрессионным моделям, содержащих в качестве объясняющей переменной зависимую переменную с единичным лагом:
Тест Дарбина-Уотсона. Ограничения Ограничения: 1. Тест не предназначен для обнаружения других видов автокорреляции (более чем первого) и не обнаруживает ее. 2. В модели должен присутствовать свободный член. 3. Данные должны иметь одинаковую периодичность (не должно быть пропусков в наблюдениях). 4. Тест не применим к авторегрессионным моделям, содержащих в качестве объясняющей переменной зависимую переменную с единичным лагом:
 Статистика Дарбина-Уотсона Статистика Дарбина-Уотсона имеет вид: T число наблюдений (обычно временных периодов) et остатки уравнения регрессии
Статистика Дарбина-Уотсона Статистика Дарбина-Уотсона имеет вид: T число наблюдений (обычно временных периодов) et остатки уравнения регрессии
 Границы для статистики Дарбина-Уотсона Можно показать, что: Отсюда следует: При положительной корреляции: При отрицательной корреляции: При отсутствии корреляции:
Границы для статистики Дарбина-Уотсона Можно показать, что: Отсюда следует: При положительной корреляции: При отрицательной корреляции: При отсутствии корреляции:
 Критические точки распределения Дарбина-Уотсона Для более точного определения, какое значение DW свидетельствует об отсутствии автокорреляции, а какое – о ее наличии, построена таблица критических точек распределения Дарбина-Уотсона. По этой таблице для заданного уровня значимости , числа наблюдений n и количества объясняющих переменных m определяются два значения: dl – нижняя граница, du – верхняя граница
Критические точки распределения Дарбина-Уотсона Для более точного определения, какое значение DW свидетельствует об отсутствии автокорреляции, а какое – о ее наличии, построена таблица критических точек распределения Дарбина-Уотсона. По этой таблице для заданного уровня значимости , числа наблюдений n и количества объясняющих переменных m определяются два значения: dl – нижняя граница, du – верхняя граница
 Расположение критических точек распределения Дарбина-Уотсона При положительной корреляции: При отрицательной корреляции: При отсутствии корреляции:
Расположение критических точек распределения Дарбина-Уотсона При положительной корреляции: При отрицательной корреляции: При отсутствии корреляции:
 Практическое использование теста Дарбина-Уотсона
Практическое использование теста Дарбина-Уотсона
 Устранение автокорреляции первого порядка (на примере парной линейной регрессии) Пусть имеем: ( известно) Процедура устранения автокорреляции остатков: Отсюда: Проблема потери первого наблюдения преодолевается с помощью поправки Прайса-Винстена:
Устранение автокорреляции первого порядка (на примере парной линейной регрессии) Пусть имеем: ( известно) Процедура устранения автокорреляции остатков: Отсюда: Проблема потери первого наблюдения преодолевается с помощью поправки Прайса-Винстена:
 Устранение автокорреляции первого порядка. Обобщения Рассмотренное авторегрессионное преобразование может быть обобщено на: 1) Произвольное число объясняющих переменных 2) Преобразования более высоких порядков AR(2), AR(3) и т.д.: Однако на практике значения коэффициента автокорреляции обычно неизвестны и его необходимо оценить. Существует несколько методов оценивания.
Устранение автокорреляции первого порядка. Обобщения Рассмотренное авторегрессионное преобразование может быть обобщено на: 1) Произвольное число объясняющих переменных 2) Преобразования более высоких порядков AR(2), AR(3) и т.д.: Однако на практике значения коэффициента автокорреляции обычно неизвестны и его необходимо оценить. Существует несколько методов оценивания.
 Способы оценивания коэффициента автокорреляции 1. На основе статистики Дарбина-Уотсона. 2. Метод Кохрана-Оркатта. 3. Метод Хилдрета-Лу. 4. Метод первых разностей.
Способы оценивания коэффициента автокорреляции 1. На основе статистики Дарбина-Уотсона. 2. Метод Кохрана-Оркатта. 3. Метод Хилдрета-Лу. 4. Метод первых разностей.
 Определение коэффициента на основе статистики Дарбина-Уотсона Этот метод дает удовлетворительные результаты при большом числе наблюдений.
Определение коэффициента на основе статистики Дарбина-Уотсона Этот метод дает удовлетворительные результаты при большом числе наблюдений.
 Итеративная процедура Кохрана-Оркатта (на примере парной регрессии) 1. Определение уравнения регрессии и вектора остатков: 2. В качестве приближенного значения берется его МНК-оценка: 3. Для найденного * оцениваются коэффициенты 0 1: 4. Подставляем в (*) и вычисляем Возвращаемся к этапу 2. Критерий остановки: разность между текущей и предыдущей оценками * стала меньше заданной точности.
Итеративная процедура Кохрана-Оркатта (на примере парной регрессии) 1. Определение уравнения регрессии и вектора остатков: 2. В качестве приближенного значения берется его МНК-оценка: 3. Для найденного * оцениваются коэффициенты 0 1: 4. Подставляем в (*) и вычисляем Возвращаемся к этапу 2. Критерий остановки: разность между текущей и предыдущей оценками * стала меньше заданной точности.
 Итеративная процедура Хилдрета-Лу (на примере парной регрессии) 1. Определение уравнения регрессии и вектора остатков: 2. Оцениваем регрессию для каждого возможного значения [1,1] с некоторым достаточно малым шагом, например 0,001; 0,01 и т.д. 3. Величина *, обеспечивающая минимум стандартной ошибки регрессии принимается в качестве оценки автокорреляции остатков.
Итеративная процедура Хилдрета-Лу (на примере парной регрессии) 1. Определение уравнения регрессии и вектора остатков: 2. Оцениваем регрессию для каждого возможного значения [1,1] с некоторым достаточно малым шагом, например 0,001; 0,01 и т.д. 3. Величина *, обеспечивающая минимум стандартной ошибки регрессии принимается в качестве оценки автокорреляции остатков.
 Итеративные процедуры оценивания коэффициента . Выводы 1. Сходимость процедур достаточно хорошая. 2. Метод Кохрана-Оркатта может «попасть» в локальный (а не глобальный) минимум. 3. Время работы процедуры Хилдрета-Лу значительно сокращается при наличии априорной информации об области возможных значений .
Итеративные процедуры оценивания коэффициента . Выводы 1. Сходимость процедур достаточно хорошая. 2. Метод Кохрана-Оркатта может «попасть» в локальный (а не глобальный) минимум. 3. Время работы процедуры Хилдрета-Лу значительно сокращается при наличии априорной информации об области возможных значений .
 Обобщенный метод наименьших квадратов (на примере парной регрессии) Пусть имеет место автокорреляция остатков:
Обобщенный метод наименьших квадратов (на примере парной регрессии) Пусть имеет место автокорреляция остатков:
 Обобщенный метод наименьших квадратов (на примере парной регрессии) Обобщенный МНК представляет собой традиционный МНК с нелинейными ограничениями типа равенств: Способы решения: 1. Решать задачу нелинейного программирования. 2. Двухшаговый МНК Дарбина. 3. Итеративная процедура расчета.
Обобщенный метод наименьших квадратов (на примере парной регрессии) Обобщенный МНК представляет собой традиционный МНК с нелинейными ограничениями типа равенств: Способы решения: 1. Решать задачу нелинейного программирования. 2. Двухшаговый МНК Дарбина. 3. Итеративная процедура расчета.
 Итеративная процедура обобщенного метода наименьших квадратов 1. Считается регрессия и находятся остатки. 2. По остаткам находят оценку коэффициента автокорреляции остатков. 3. Оценка коэффициента автокорреляции используется для пересчета данных и цикл повторяется. Процесс останавливается, как только обеспечивается достаточная точность (результаты перестают существенно улучшаться).
Итеративная процедура обобщенного метода наименьших квадратов 1. Считается регрессия и находятся остатки. 2. По остаткам находят оценку коэффициента автокорреляции остатков. 3. Оценка коэффициента автокорреляции используется для пересчета данных и цикл повторяется. Процесс останавливается, как только обеспечивается достаточная точность (результаты перестают существенно улучшаться).
 Обобщенный метод наименьших квадратов. Замечания 1. Значимый коэффициент DW может указывать просто на ошибочную спецификацию. 2. Последствия автокорреляции остатков иногда бывают незначительными. 3. Качество оценок может снизиться из-за уменьшения числа степеней свободы (нужно оценивать дополнительный параметр). 4. Значительно возрастает трудоемкость расчетов. Не следует применять обобщенный МНК автоматически
Обобщенный метод наименьших квадратов. Замечания 1. Значимый коэффициент DW может указывать просто на ошибочную спецификацию. 2. Последствия автокорреляции остатков иногда бывают незначительными. 3. Качество оценок может снизиться из-за уменьшения числа степеней свободы (нужно оценивать дополнительный параметр). 4. Значительно возрастает трудоемкость расчетов. Не следует применять обобщенный МНК автоматически
 Вопросы для самопроверки Что такое автокорреляция ошибок. Приведите пример пространственной автокорреляции. Из-за чего может возникнуть автокорреляция в модели. Какие последствия наличия автокорреляции в модели. В каком случае МНК коэффициенты будут несостоятельны, если в модели присутствует автокорреляция. Как выглядит матрица ковариаций ошибок в случае наличия автокорреляции. При каких условиях можно использовать тест Дарбина-Уотсона для обнаружения автокорреляции. Какие вы знаете еще тесты для обнаружения автокорреляции. Как обнаружить автокорреляцию графически. Как корректировать модель при наличии автокорреляции. Для чего нужна поправка Прайса-Уинсена.
Вопросы для самопроверки Что такое автокорреляция ошибок. Приведите пример пространственной автокорреляции. Из-за чего может возникнуть автокорреляция в модели. Какие последствия наличия автокорреляции в модели. В каком случае МНК коэффициенты будут несостоятельны, если в модели присутствует автокорреляция. Как выглядит матрица ковариаций ошибок в случае наличия автокорреляции. При каких условиях можно использовать тест Дарбина-Уотсона для обнаружения автокорреляции. Какие вы знаете еще тесты для обнаружения автокорреляции. Как обнаружить автокорреляцию графически. Как корректировать модель при наличии автокорреляции. Для чего нужна поправка Прайса-Уинсена.
 Тема 14.Временные ряды Time series
Тема 14.Временные ряды Time series
 Темы лекции. Стационарные и нестационарные временные ряды Обнаружение нестационарности Модели стационарных временных рядов
Темы лекции. Стационарные и нестационарные временные ряды Обнаружение нестационарности Модели стационарных временных рядов
 Стационарность ряда Ряд называется строго стационарным, если совместное распределение вероятностей ,…, не зависит от сдвига по времени, т. е. совпадает с распределением вероятностей ,…, для любых L, t1,…,tm.
Стационарность ряда Ряд называется строго стационарным, если совместное распределение вероятностей ,…, не зависит от сдвига по времени, т. е. совпадает с распределением вероятностей ,…, для любых L, t1,…,tm.
 Слабая стационарность Ряд называется слабо стационарным или просто стационарным, если средние, дисперсии и ковариации не зависят от времени t. Таким образом, для стационарного ряда
Слабая стационарность Ряд называется слабо стационарным или просто стационарным, если средние, дисперсии и ковариации не зависят от времени t. Таким образом, для стационарного ряда
 Автокорреляционная функция ряда Выборочная автокорреляционная функция временного ряда называется коррелограммой и определяется следующим образом:
Автокорреляционная функция ряда Выборочная автокорреляционная функция временного ряда называется коррелограммой и определяется следующим образом:
 Частная автокорреляционная функция Кроме автокорреляционной функции рассматривают еще частную автокорреляционную функцию PACFY(L). Содержательно частная автокорреляционная функция представляет собой «чистую корреляцию» между Yt и Yt+L при исключении влияний промежуточных значений Yt+1,…,Yt+L1. Формула для ее записи достаточно сложна, поэтому здесь мы ее не приводим.
Частная автокорреляционная функция Кроме автокорреляционной функции рассматривают еще частную автокорреляционную функцию PACFY(L). Содержательно частная автокорреляционная функция представляет собой «чистую корреляцию» между Yt и Yt+L при исключении влияний промежуточных значений Yt+1,…,Yt+L1. Формула для ее записи достаточно сложна, поэтому здесь мы ее не приводим.
 Примеры временных рядов «белый шум» – все уровни временного ряда распределены одинаково. где MYt = 0, DYt =2 , .
Примеры временных рядов «белый шум» – все уровни временного ряда распределены одинаково. где MYt = 0, DYt =2 , .
 Белый шум
Белый шум
 Примеры временных рядов (продолжение)
Примеры временных рядов (продолжение)
 Примеры временных рядов (продолжение) авторегрессионный ряд первого порядка (AR(1)) . если ряд стационарен.
Примеры временных рядов (продолжение) авторегрессионный ряд первого порядка (AR(1)) . если ряд стационарен.
 AR(1)
AR(1)
 Примеры временных рядов (продолжение) «случайное блуждание» . Дисперсия ряда неограниченно возрастает со временем. Ряд не является стационарным.
Примеры временных рядов (продолжение) «случайное блуждание» . Дисперсия ряда неограниченно возрастает со временем. Ряд не является стационарным.
 Примеры временных рядов (продолжение) ряд с трендом, например, линейным. ряд не является стационарным.
Примеры временных рядов (продолжение) ряд с трендом, например, линейным. ряд не является стационарным.
 Примеры временных рядов (продолжение) ряд с сезонной компонентой не является стационарным.
Примеры временных рядов (продолжение) ряд с сезонной компонентой не является стационарным.
 Ряд с трендом и сезонностью
Ряд с трендом и сезонностью
 Трендовая нестационарность В случае 4) и 5) методы моделирования стационарных временных рядов применяются к остаткам регрессии или к сглаженным уровням временного ряда, т.е. к уровням, очищенным от тренда, циклической и сезонной составляющей.
Трендовая нестационарность В случае 4) и 5) методы моделирования стационарных временных рядов применяются к остаткам регрессии или к сглаженным уровням временного ряда, т.е. к уровням, очищенным от тренда, циклической и сезонной составляющей.
 Обнаружение нестационарности 1. Визуальный анализ временного ряда. Возможно, временной ряд содержит видный на глаз временной тренд и сезонность (периодичную компоненту). Возможно, что разброс значений возрастает или убывает со временем (признак «случайного блуждания»). Это может служить указанием на зависимость среднего и, соответственно, дисперсии от времени. Во всех трех случаях ряд, скорее всего, не будет стационарным.
Обнаружение нестационарности 1. Визуальный анализ временного ряда. Возможно, временной ряд содержит видный на глаз временной тренд и сезонность (периодичную компоненту). Возможно, что разброс значений возрастает или убывает со временем (признак «случайного блуждания»). Это может служить указанием на зависимость среднего и, соответственно, дисперсии от времени. Во всех трех случаях ряд, скорее всего, не будет стационарным.
 Обнаружение нестационарности (продолжение) 2. Построить график выборочной автокорреляционной функции или коррелограмму. Коррелограмма стационарного временного ряда быстро убывает со временем, быстро уходит почти в ноль после нескольких первых значений – «влияние предыдущих уровней затухает». Если график показывает, что ACF убывает медленно, с колебаниями, то ряд, скорее всего, будет нестационарным.
Обнаружение нестационарности (продолжение) 2. Построить график выборочной автокорреляционной функции или коррелограмму. Коррелограмма стационарного временного ряда быстро убывает со временем, быстро уходит почти в ноль после нескольких первых значений – «влияние предыдущих уровней затухает». Если график показывает, что ACF убывает медленно, с колебаниями, то ряд, скорее всего, будет нестационарным.
 Обнаружение нестационарности (продолжение) 3. Формальные тесты на стационарность (тест Дикки-Фуллера)
Обнаружение нестационарности (продолжение) 3. Формальные тесты на стационарность (тест Дикки-Фуллера)
 Избавление от нестационарности Выделить тренд и сезонность, т. е. неслучайную составляющую временного ряда. Если ряд представляет «случайное блуждание», то взятие последовательных разностей делает ряд стационарным. На практике порядок разностей, как правило, не больше двух.
Избавление от нестационарности Выделить тренд и сезонность, т. е. неслучайную составляющую временного ряда. Если ряд представляет «случайное блуждание», то взятие последовательных разностей делает ряд стационарным. На практике порядок разностей, как правило, не больше двух.
 Модели стационарных временных рядов Модели Бокса-Дженкинса. Модели авторегрессии и скользящего среднего ARMA(p,q)
Модели стационарных временных рядов Модели Бокса-Дженкинса. Модели авторегрессии и скользящего среднего ARMA(p,q)
 ARMA(p,q) процесс авторегрессии порядка p и скользящего среднего порядка q –ARMA(p,q) авторегрессионный член порядка p член скользящего среднего порядка q
ARMA(p,q) процесс авторегрессии порядка p и скользящего среднего порядка q –ARMA(p,q) авторегрессионный член порядка p член скользящего среднего порядка q
 Анализ стационарных временных рядов Спецификация ARMA-моделей. Оценивание модели. Проверка адекватности модели. Прогнозирование на основе построенной модели.
Анализ стационарных временных рядов Спецификация ARMA-моделей. Оценивание модели. Проверка адекватности модели. Прогнозирование на основе построенной модели.
 Спецификация ARMA-моделей. Определение p и q. Для этого можно построить графики автокорреляционной функции и частной автокорреляционной функции ряда для того, чтобы определить подходящие значения p и q. Автокорерляционные функции и частные автокорреляционные функции процессов AR(1), AR(2), MA(1), MA(2) и ARMA(1,1) легко опознать.
Спецификация ARMA-моделей. Определение p и q. Для этого можно построить графики автокорреляционной функции и частной автокорреляционной функции ряда для того, чтобы определить подходящие значения p и q. Автокорерляционные функции и частные автокорреляционные функции процессов AR(1), AR(2), MA(1), MA(2) и ARMA(1,1) легко опознать.
 Спецификация ARMA-моделей (продолжение) На этом этапе мы можем сформулировать несколько гипотез относительно возможных значениях порядков p и q. Для подходящих значений автокорреляционная функция остатков ARMA(p,q) – модели похожа на «белый шум».
Спецификация ARMA-моделей (продолжение) На этом этапе мы можем сформулировать несколько гипотез относительно возможных значениях порядков p и q. Для подходящих значений автокорреляционная функция остатков ARMA(p,q) – модели похожа на «белый шум».
 Оценивание модели В современные пакеты встроены различные методы оценивания ARIMA – моделей, такие как линейный или нелинейный МНК. полный или условный метод максимального правдоподобия.
Оценивание модели В современные пакеты встроены различные методы оценивания ARIMA – моделей, такие как линейный или нелинейный МНК. полный или условный метод максимального правдоподобия.
 Проверка адекватности модели Необходимо проверить правильность предположений относительно параметров модели. Для этого проверяем статистическую значимость коэффициентов модели должны достоверно отличатся от нуля проверяем отсутствие автокорреляции в остатках ARMA(p,q) – модели
Проверка адекватности модели Необходимо проверить правильность предположений относительно параметров модели. Для этого проверяем статистическую значимость коэффициентов модели должны достоверно отличатся от нуля проверяем отсутствие автокорреляции в остатках ARMA(p,q) – модели
 Вопросы для самопроверки Что такое временной ряд. Определение сильно стационарного ряда. Определение слабо стационарного ряда. Что такое автокорреляционная функция ряда. Что такое тренд. Приведите примеры стационарных и нестационарных временных рядов. Как проверить стационарность ряда. Какие вы знаете типы нестационарных рядов. Приведите примеры. Чем нам грозит регрессия одного стационарного ряда на другой. Что такое ARMA представление стационарного ряда. Как подобрать адекватную ARMA модель ряда.
Вопросы для самопроверки Что такое временной ряд. Определение сильно стационарного ряда. Определение слабо стационарного ряда. Что такое автокорреляционная функция ряда. Что такое тренд. Приведите примеры стационарных и нестационарных временных рядов. Как проверить стационарность ряда. Какие вы знаете типы нестационарных рядов. Приведите примеры. Чем нам грозит регрессия одного стационарного ряда на другой. Что такое ARMA представление стационарного ряда. Как подобрать адекватную ARMA модель ряда.
 Тема 15. Системы одновременных уравнений. СОУ
Тема 15. Системы одновременных уравнений. СОУ
 Темы лекции Системы одновременных уравнений Структурная и приведенная формы уравнений Проблема идентификации Методы оценивания СОУ Внешне не связанные уравнения
Темы лекции Системы одновременных уравнений Структурная и приведенная формы уравнений Проблема идентификации Методы оценивания СОУ Внешне не связанные уравнения
 СИСТЕМЫ РЕГРЕССИОННЫХ УРАВНЕНИЙ Интересующие зависимости описываются системой взаимосвязанных соотношений. системы одновременных уравнений (simultaneous equations); системы внешне не связанных уравнений (seemingly unrelated regression (SUR))
СИСТЕМЫ РЕГРЕССИОННЫХ УРАВНЕНИЙ Интересующие зависимости описываются системой взаимосвязанных соотношений. системы одновременных уравнений (simultaneous equations); системы внешне не связанных уравнений (seemingly unrelated regression (SUR))
 СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ Пример 1. уравнение предложения: уравнение спроса: условие равновесия на рынке: , P – цена на товар, Y – доход, Q – количество товара
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ Пример 1. уравнение предложения: уравнение спроса: условие равновесия на рынке: , P – цена на товар, Y – доход, Q – количество товара
 Основные вопросы, возникающие при рассмотрении СОУ: идентификация системы; методы оценивания (применимость методов оценивания автономных уравнений (МНК или ОМНК)). ОМНК НЕ ПРИМЕНИМ!!!!!!! Применение ОМНК для оценки каждого уравнения системы по отдельности приводит к смещенным и несостоятельным оценкам.
Основные вопросы, возникающие при рассмотрении СОУ: идентификация системы; методы оценивания (применимость методов оценивания автономных уравнений (МНК или ОМНК)). ОМНК НЕ ПРИМЕНИМ!!!!!!! Применение ОМНК для оценки каждого уравнения системы по отдельности приводит к смещенным и несостоятельным оценкам.
 Пример 2 C – потребительские расходы, Y – доход, Z – непотребительские расходы.
Пример 2 C – потребительские расходы, Y – доход, Z – непотребительские расходы.
 Пример 2 (продолжение) Из первого уравнения подставим Ct во второе:
Пример 2 (продолжение) Из первого уравнения подставим Ct во второе:
 Переменные в СОУ эндогенные; экзогенные; предопределенные (экзогенные переменные и лаговые значения эндогенных переменных).
Переменные в СОУ эндогенные; экзогенные; предопределенные (экзогенные переменные и лаговые значения эндогенных переменных).
 Уравнения системы Уравнения, составляющие исходную модель, называются структурными уравнениями модели. поведенческие уравнения; уравнения тождества. Уравнения, в левой части которых находится эндогенная переменная, а в правой – только предопределенные переменные и случайный член – уравнения в приведенной форме.
Уравнения системы Уравнения, составляющие исходную модель, называются структурными уравнениями модели. поведенческие уравнения; уравнения тождества. Уравнения, в левой части которых находится эндогенная переменная, а в правой – только предопределенные переменные и случайный член – уравнения в приведенной форме.
 КМНК Косвенный метод наименьших квадратов (КМНК) - ОМНК, примененный к уравнениям в приведенной форме. НО ВОЗНИКАЕТ ПРОБЛЕМА ИДЕНТИФИКАЦИИ
КМНК Косвенный метод наименьших квадратов (КМНК) - ОМНК, примененный к уравнениям в приведенной форме. НО ВОЗНИКАЕТ ПРОБЛЕМА ИДЕНТИФИКАЦИИ
 Пример 2 (продолжение) ’ и ’ ОМНК a’ и b’
Пример 2 (продолжение) ’ и ’ ОМНК a’ и b’
 Пример 2 (продолжение) Возвращаясь к исходному уравнению, получим оценки для параметров и : Получили два уравнения для двух неизвестных
Пример 2 (продолжение) Возвращаясь к исходному уравнению, получим оценки для параметров и : Получили два уравнения для двух неизвестных
 Возможные ситуации нельзя получить единственные значения коэффициентов структурного уравнения. В этом случае уравнение называют неопределенным – неидентифицируемым; нельзя получит никакого решения – в случае переопределенного (сверхидентифицируемого) уравнения
Возможные ситуации нельзя получить единственные значения коэффициентов структурного уравнения. В этом случае уравнение называют неопределенным – неидентифицируемым; нельзя получит никакого решения – в случае переопределенного (сверхидентифицируемого) уравнения
 Неидентифицируемость Модель 1 - уравнение спроса, - уравнение предложения P – цена товара, X – доход на душу населения
Неидентифицируемость Модель 1 - уравнение спроса, - уравнение предложения P – цена товара, X – доход на душу населения
 Уравнения в приведенной форме
Уравнения в приведенной форме
 Применяем КМНК
Применяем КМНК
 Некоторые результаты Получили четыре уравнения для пяти неизвестных оценка e из второго и четвертого соотношений первое и третье соотношение дают нам оценку d
Некоторые результаты Получили четыре уравнения для пяти неизвестных оценка e из второго и четвертого соотношений первое и третье соотношение дают нам оценку d
 Графическая иллюстрация Модели 1 КМНК: кривая спроса неидентифицируема
Графическая иллюстрация Модели 1 КМНК: кривая спроса неидентифицируема
 Неидентифицируемость Модель 2 - уравнение спроса, - уравнение предложения P – цена товара,
Неидентифицируемость Модель 2 - уравнение спроса, - уравнение предложения P – цена товара,
 Приведенная форма уравнений После оценивания КМНК получим два уравнения на четыре неизвестных
Приведенная форма уравнений После оценивания КМНК получим два уравнения на четыре неизвестных
 Графическая иллюстрация Модели 2 КМНК: оба уравнения неидентифицируемы.
Графическая иллюстрация Модели 2 КМНК: оба уравнения неидентифицируемы.
 Сверхидентифицируемость Модель 3 - уравнение спроса, - уравнение предложения W – любая переменная по смыслу
Сверхидентифицируемость Модель 3 - уравнение спроса, - уравнение предложения W – любая переменная по смыслу
 Приведенная форма уравнений Переобозначим
Приведенная форма уравнений Переобозначим
 Сверхидентифицируемость дают оценку . Они могут совпасть только случайным образом. Для - аналогичная ситуация. На оценку уравнения спроса осталось два соотношения на четыре переменные. Уравнение спроса неопределенно
Сверхидентифицируемость дают оценку . Они могут совпасть только случайным образом. Для - аналогичная ситуация. На оценку уравнения спроса осталось два соотношения на четыре переменные. Уравнение спроса неопределенно
 ХОТИМ ИМЕТЬ КРИТЕРИЙ ИДЕНТИФИЦИРУЕМОСТИ УРАВНЕНИЙ
ХОТИМ ИМЕТЬ КРИТЕРИЙ ИДЕНТИФИЦИРУЕМОСТИ УРАВНЕНИЙ
 Необходимое условие идентифицируемости Если уравнение в СОУ идентифицируемо, то число предопределенных переменных, не присутствующих в уравнении, должно быть не меньше (больше или равно) числу входящих в уравнение эндогенных переменных минус 1. В это число входят как левосторонние, так и правосторонние эндогенные переменные.
Необходимое условие идентифицируемости Если уравнение в СОУ идентифицируемо, то число предопределенных переменных, не присутствующих в уравнении, должно быть не меньше (больше или равно) числу входящих в уравнение эндогенных переменных минус 1. В это число входят как левосторонние, так и правосторонние эндогенные переменные.
 Системы внешне не связанных уравнений (SUR) Yi, Xij и i - вектора, состоящие из N компонент, Всего Nm наблюдений и k1+…+km+ m регрессоров.
Системы внешне не связанных уравнений (SUR) Yi, Xij и i - вектора, состоящие из N компонент, Всего Nm наблюдений и k1+…+km+ m регрессоров.
 Спецификация ошибок Ошибки: в каждом уравнении системы удовлетворяет условиям Гаусса-Маркова; разных уравнений коррелируют между собой следующим образом: ошибки, относящиеся к разным индивидуумам коррелируют в один и тот же момент времени и не коррелируют в разные моменты времени
Спецификация ошибок Ошибки: в каждом уравнении системы удовлетворяет условиям Гаусса-Маркова; разных уравнений коррелируют между собой следующим образом: ошибки, относящиеся к разным индивидуумам коррелируют в один и тот же момент времени и не коррелируют в разные моменты времени
 Методы оценивания МНК к каждому уравнению системы по отдельности. ОМНК к системе в целом, что улучшит эффективность оценивания; позволит осуществить проверку гипотез об ограничениях на коэффициенты в разных уравнениях.
Методы оценивания МНК к каждому уравнению системы по отдельности. ОМНК к системе в целом, что улучшит эффективность оценивания; позволит осуществить проверку гипотез об ограничениях на коэффициенты в разных уравнениях.
 Матрица ковариаций ошибок
Матрица ковариаций ошибок
 ОМНК
ОМНК
 ОМНК и МНК ОМНК и МНК оценки совпадают: уравнения действительно не связаны друг с другом, т. е. =0, i j; все уравнения имеют один и тот же набор объясняющих переменных. Эффективность ОМНК-оценки по сравнению с МНК-оценками тем выше, чем сильнее корреляция между ошибками.
ОМНК и МНК ОМНК и МНК оценки совпадают: уравнения действительно не связаны друг с другом, т. е. =0, i j; все уравнения имеют один и тот же набор объясняющих переменных. Эффективность ОМНК-оценки по сравнению с МНК-оценками тем выше, чем сильнее корреляция между ошибками.
 Оценка матрицы Применяем обычный МНК к каждому уравнению, получая векторы остатков е для каждого уравнения. В качестве оценки берем величину Эти оценки состоятельны
Оценка матрицы Применяем обычный МНК к каждому уравнению, получая векторы остатков е для каждого уравнения. В качестве оценки берем величину Эти оценки состоятельны
 Вопросы для самопроверки Приведите примеры систем одновременных уравнений. Классификация переменных в системах одновременных уравнений. Что такое структурная форма уравнений системы. Что такое приведенные уравнения. Для каких переменных выводят приведенные уравнения. Что такое проблема идентифицируемости. Приведите пример идентифицируемых уравнений. Приведите пример неентифицируемых уравнений Приведите пример сверхидентифицируемых уравнений. Какие вы знаете критерии идентифицируемости уравнений. Какие регрессионные модели являются системами внешне не связанных уравнений. Преимущества рассмотрения набора уравнений как системы Способы оценки SUR. В каком случае МНК и ДОМНК-оценки совпадают. Как состоятельно оценить матрицу ковариаций ошибок.
Вопросы для самопроверки Приведите примеры систем одновременных уравнений. Классификация переменных в системах одновременных уравнений. Что такое структурная форма уравнений системы. Что такое приведенные уравнения. Для каких переменных выводят приведенные уравнения. Что такое проблема идентифицируемости. Приведите пример идентифицируемых уравнений. Приведите пример неентифицируемых уравнений Приведите пример сверхидентифицируемых уравнений. Какие вы знаете критерии идентифицируемости уравнений. Какие регрессионные модели являются системами внешне не связанных уравнений. Преимущества рассмотрения набора уравнений как системы Способы оценки SUR. В каком случае МНК и ДОМНК-оценки совпадают. Как состоятельно оценить матрицу ковариаций ошибок.
 Тема 16. Методы оценивания СОУ
Тема 16. Методы оценивания СОУ
 Темы лекции Косвенный МНК Метод инструментальных переменных Двухшаговый МНК
Темы лекции Косвенный МНК Метод инструментальных переменных Двухшаговый МНК
 Косвенный метод наименьших квадратов КМНК – проблема идентифицируемости. Если интересует прогноз значений эндогенных переменных, то можно применять. Упражнение. Показать, что в случае идентифицируемого уравнения КМНК-оценки совпадут с оценками по методу инструментальных переменных. КМНК-оценки для идентифицируемых уравнений в общем случае смещены; состоятельны.
Косвенный метод наименьших квадратов КМНК – проблема идентифицируемости. Если интересует прогноз значений эндогенных переменных, то можно применять. Упражнение. Показать, что в случае идентифицируемого уравнения КМНК-оценки совпадут с оценками по методу инструментальных переменных. КМНК-оценки для идентифицируемых уравнений в общем случае смещены; состоятельны.
 Метод инструментальных переменных Метод оценивания уравнений со случайным членом, коррелирующим с регрессорами. Суть метода – частичная замена непригодной объясняющей переменной той переменной, которая некоррелированна со случайным членом. Парная линейная модель: где X и коррелированны
Метод инструментальных переменных Метод оценивания уравнений со случайным членом, коррелирующим с регрессорами. Суть метода – частичная замена непригодной объясняющей переменной той переменной, которая некоррелированна со случайным членом. Парная линейная модель: где X и коррелированны
 Проблема смещения оценка смещена и несостоятельна
Проблема смещения оценка смещена и несостоятельна
 Оценка по методу ИП Переменная Z коррелирует с Х и некоррелирует с
Оценка по методу ИП Переменная Z коррелирует с Х и некоррелирует с
 Состоятельность? Для того чтобы оценка была состоятельной, необходимо, чтобы , т. е. необходимо наличие «сильной» корреляции между переменными X и Z.
Состоятельность? Для того чтобы оценка была состоятельной, необходимо, чтобы , т. е. необходимо наличие «сильной» корреляции между переменными X и Z.
 Где взять ИП? Трудность - отыскание переменных, пригодных к роли инструментов для Х. Они должны быть сильно коррелированны с Х и совсем некоррелированны с . Для СОУ в качестве инструментальных переменных берутся предопределенные переменные. Они коррелируют с эндогенными переменными, поскольку являются частью модели; некоррелируют со случайным членом по определению
Где взять ИП? Трудность - отыскание переменных, пригодных к роли инструментов для Х. Они должны быть сильно коррелированны с Х и совсем некоррелированны с . Для СОУ в качестве инструментальных переменных берутся предопределенные переменные. Они коррелируют с эндогенными переменными, поскольку являются частью модели; некоррелируют со случайным членом по определению
 Модель 1 Единственная предопределенная переменная Х. Ее берем в качестве инструментальной для Р в уравнении предложения. Уравнение спроса по-прежнему неидентифицируемо
Модель 1 Единственная предопределенная переменная Х. Ее берем в качестве инструментальной для Р в уравнении предложения. Уравнение спроса по-прежнему неидентифицируемо
 Модель 4 Х – инструмент для Р в уравнении предложения, T – инструмент для Р в уравнении спроса. Получим состоятельные оценки коэффициентов обоих уравнений.
Модель 4 Х – инструмент для Р в уравнении предложения, T – инструмент для Р в уравнении спроса. Получим состоятельные оценки коэффициентов обоих уравнений.
 Модель 3 Две предопределенные переменные – X и Z, обе они фигурируют в уравнении спроса и обе подходят в качестве инструмента для Р в уравнении предложения. Уравнение спроса по-прежнему не определено
Модель 3 Две предопределенные переменные – X и Z, обе они фигурируют в уравнении спроса и обе подходят в качестве инструмента для Р в уравнении предложения. Уравнение спроса по-прежнему не определено
 Итак, Метод инструментальных переменных может помочь в случае идентифицируемых уравнений сверхидентифицируемых уравнений (проблема выбора инструмента)
Итак, Метод инструментальных переменных может помочь в случае идентифицируемых уравнений сверхидентифицируемых уравнений (проблема выбора инструмента)
 Двухшаговый метод наименьших квадратов (ДМНК). Модель 3 – проблема выбора инструмента для переменной Р в уравнении предложения из двух подходящих переменных. Идея ДМНК - вместо раздельного использования подходящих для инструмента переменных построить их линейную комбинацию таким образом, чтобы максимизировать значение коэффициента корреляции между этим новым инструментом и заменяемой переменной
Двухшаговый метод наименьших квадратов (ДМНК). Модель 3 – проблема выбора инструмента для переменной Р в уравнении предложения из двух подходящих переменных. Идея ДМНК - вместо раздельного использования подходящих для инструмента переменных построить их линейную комбинацию таким образом, чтобы максимизировать значение коэффициента корреляции между этим новым инструментом и заменяемой переменной
 Новый инструмент В качестве инструмента берем прогнозные значения Р в регрессии Р на X и W
Новый инструмент В качестве инструмента берем прогнозные значения Р в регрессии Р на X и W
 Алгоритм ДМНК 1. Построение инструмента для эндогенной переменной. Для этого нам надо осуществить регрессию по методу наименьших квадратов этой переменной на все предопределенные переменные в модели и вычислить прогнозные значения для этой переменной. По построению новый инструмент и случайные члены исходной модели не будут коррелировать (строго говоря, это справедливо лишь для достаточно больших выборок, так что здесь мы можем завести разговор о состоятельности ДМНК). Таким образом, на первом шаге мы построили новую переменную, которая линейно связана со всеми предопределенными переменными и очищена от корреляции с ошибками во всех уравнениях структурной модели.
Алгоритм ДМНК 1. Построение инструмента для эндогенной переменной. Для этого нам надо осуществить регрессию по методу наименьших квадратов этой переменной на все предопределенные переменные в модели и вычислить прогнозные значения для этой переменной. По построению новый инструмент и случайные члены исходной модели не будут коррелировать (строго говоря, это справедливо лишь для достаточно больших выборок, так что здесь мы можем завести разговор о состоятельности ДМНК). Таким образом, на первом шаге мы построили новую переменную, которая линейно связана со всеми предопределенными переменными и очищена от корреляции с ошибками во всех уравнениях структурной модели.
 Алгоритм ДМНК (продолжение) 2. Переменная, полученная на первом шаге, используется в качестве инструментальной для эндогенной переменной в структурной модели. Вычисляются оценки коэффициентов структурного уравнения по методу инструментальных переменных. Эти оценки состоятельны. ДМНК справляется проблемой сверхидентифицируемости. В случае же идентифицируемости оценки по ДМНК совпадают с оценками КМНК и МИП.
Алгоритм ДМНК (продолжение) 2. Переменная, полученная на первом шаге, используется в качестве инструментальной для эндогенной переменной в структурной модели. Вычисляются оценки коэффициентов структурного уравнения по методу инструментальных переменных. Эти оценки состоятельны. ДМНК справляется проблемой сверхидентифицируемости. В случае же идентифицируемости оценки по ДМНК совпадают с оценками КМНК и МИП.
 Оценивание СОУ с автокоррелированными ошибками Лаговые переменные не являются предопределенными. МНК и ДМНК несостоятельны.
Оценивание СОУ с автокоррелированными ошибками Лаговые переменные не являются предопределенными. МНК и ДМНК несостоятельны.
 Вопросы для самопроверки Что такое КМНК. Почему метод наименьших квадратов не применим при оценивании систем регрессионных уравнений. Какой метод применяется если регрессоры в уравнении коррелируют с ошибками. В какм случае оценки ИП и МНК совпадают. Что делать в случае неидентифицируемого уравнения. Основная идея ДМНК. Как сконструировать оптимальный инструмент. Какие переменные можно взять в качестве инструментальных в системах регрессионных уравнений. Что такое «хороший инструмент». Какие проблемы возникают в случае наличия автокорреляции в ошибках уравнений системы.
Вопросы для самопроверки Что такое КМНК. Почему метод наименьших квадратов не применим при оценивании систем регрессионных уравнений. Какой метод применяется если регрессоры в уравнении коррелируют с ошибками. В какм случае оценки ИП и МНК совпадают. Что делать в случае неидентифицируемого уравнения. Основная идея ДМНК. Как сконструировать оптимальный инструмент. Какие переменные можно взять в качестве инструментальных в системах регрессионных уравнений. Что такое «хороший инструмент». Какие проблемы возникают в случае наличия автокорреляции в ошибках уравнений системы.

