Structured Overlays — self-organization and scalability Acknowledgement based

Structured Overlays - self-organization and scalability Acknowledgement: based on slides by Anwitaman Datta–Nanyang and Ali Ghodsi 1

Self-organization • Self-organizing systems common in nature – Physics, biology, economics, sociology, cybernatics – Microscopic (local) interactions – Limited information, individual decisions • Distribution of control => decentralization – Symmetry in roles/peer-to-peer – Emergence of macroscopic (global) properties • Resilience – Fault tolerance as well as recovery – Adaptivity 2

A Distributed Systems Perspective (P 2 P) • Centralized solutions undesirable or unattainable • Exploit resources at the edge - no dedicated infrastructure/servers - peers act as both clients and servers (servent) • Autonomous participants - large scale - dynamic system and workload - source of unpredictability - e. g. , correlated failures • No global control or knowledge - rely on self-organization 3

One solution: structured overlays/ distributed hash tables 4

What’s a Distributed Hash Table? • An ordinary hash table , which is distributed Key Value Anwitaman Singapore Ali Berkeley Alberto Trento Kurt Kassel Ozalp Bologna Randy Berkeley • Every node provides a lookup operation –Given a key: return the associated value • Nodes keep routing pointers –If item not found locally, route to another node 5

Why’s that interesting? • Characteristic properties – Self-management in presence joins/leaves/failures • Routing information • Data items – Scalability • Number of nodes can be huge (to store a huge number of items) • However: search and maintenance costs scale sub-linearly (often logarithmically) with the number of nodes. 6

short interlude applications 7

Global File System • Similar to DFS (eg NFS, AFS) – But files/metadata stored in directory – E. g. Wuala, Wheel. FS… node A Key /home/. . . • What is new? Value 130. 237. 32. 51 /usr/… 193. 10. 64. 99 /boot/… 18. 7. 22. 83 /etc/… … 128. 178. 50. 12 … node B node D node C – Application logic self-managed • Add/remove servers on the fly • Automatic faliure handling • Automatic load-balancing – No manual configuration for these ops 8

P 2 P Web Servers • Distributed community Web Server – Pages stored in the directory node A Key www. s. . . 130. 237. 32. 51 www 2 • What is new? Value 193. 10. 64. 99 www 3 18. 7. 22. 83 cs. edu 128. 178. 50. 12 … … node B node D node C – Application logic self-managed • Automatically load-balances • Add/remove servers on the fly • Automatically handles failures • Example: – Coral. CDN 9

Name-based communication Pattern • Map node names to location – Can store all kinds of contact information • Mediator peers for NAT hole punching • Profile information Key anwita 193. 10. 64. 99 alberto 18. 7. 22. 83 ozalp • Used this way by: 130. 237. 32. 51 ali 128. 178. 50. 12 … … node A Value node B node D node C – Internet Indirection Infrastructure (i 3) – Host Identity Payload (HIP) – P 2 P Session Initiation Protocol (P 2 PSIP) 10

towards DHT construction consistent hashing 11

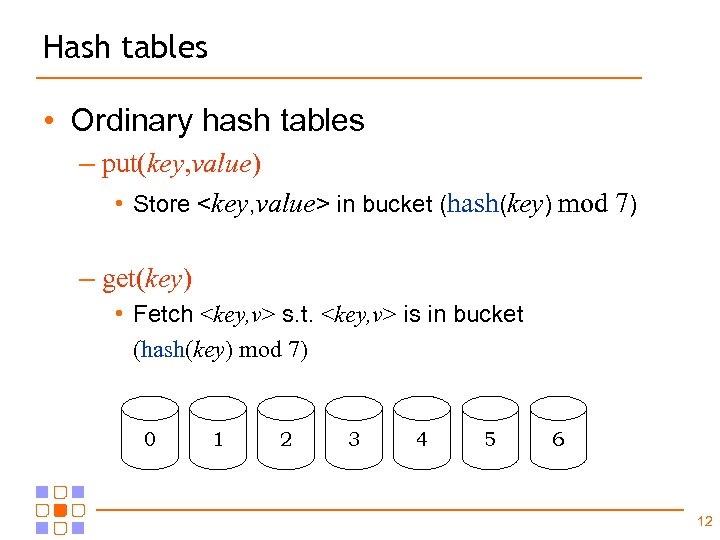
Hash tables • Ordinary hash tables – put(key, value) • Store <key, value> in bucket (hash(key) mod 7) – get(key) • Fetch <key, v> s. t. <key, v> is in bucket (hash(key) mod 7) 0 1 2 3 4 5 6 12

DHT by mimicking Hash Tables • Let each bucket be a server – n servers means n buckets • Problem – How do we remove or add buckets? – A single bucket change requires re-shuffling a large fraction of items 13

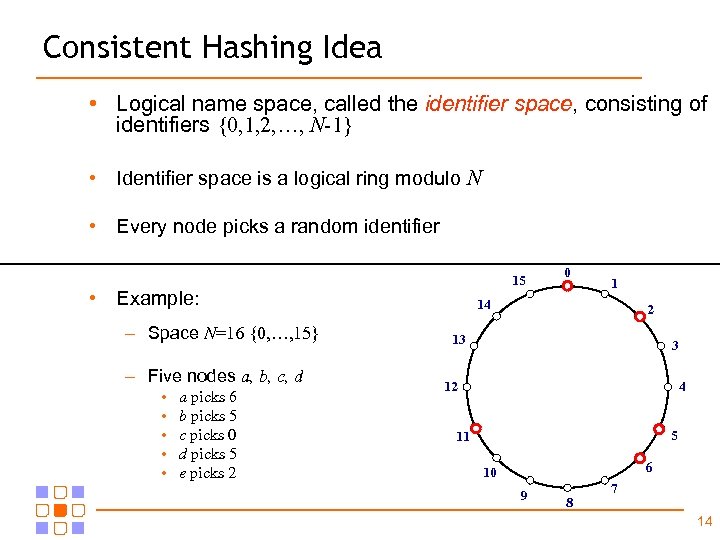
Consistent Hashing Idea • Logical name space, called the identifier space, consisting of identifiers {0, 1, 2, …, N-1} • Identifier space is a logical ring modulo N • Every node picks a random identifier 15 • Example: – Space N=16 {0, …, 15} – Five nodes a, b, c, d • • • a picks 6 b picks 5 c picks 0 d picks 5 e picks 2 0 1 14 2 13 3 12 4 5 11 6 10 9 8 7 14

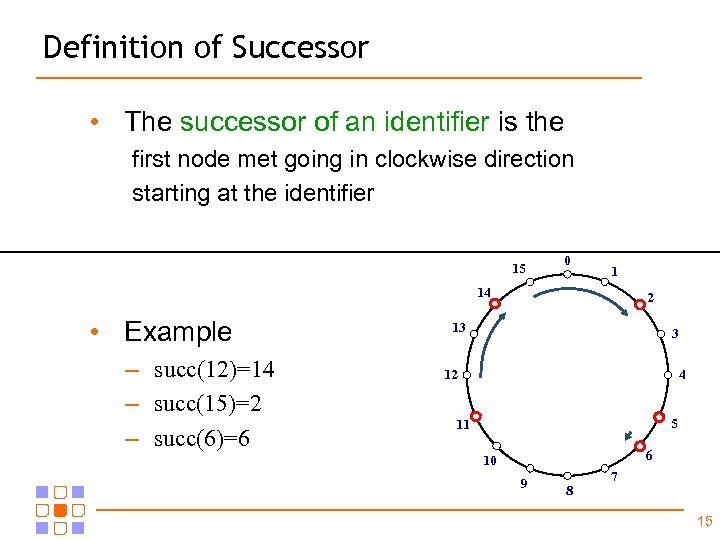
Definition of Successor • The successor of an identifier is the first node met going in clockwise direction starting at the identifier 15 0 1 14 • Example – succ(12)=14 – succ(15)=2 – succ(6)=6 2 13 3 12 4 5 11 6 10 9 8 7 15

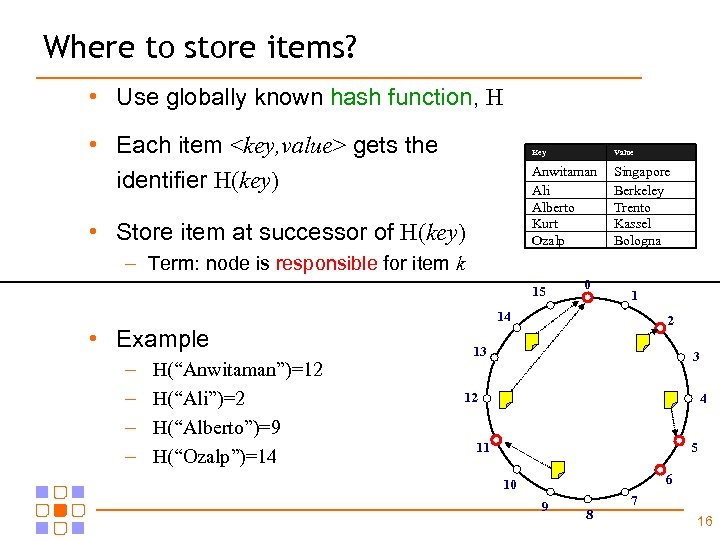
Where to store items? • Use globally known hash function, H • Each item <key, value> gets the identifier H(key) Key Anwitaman Ali Alberto Kurt Ozalp • Store item at successor of H(key) Value Singapore Berkeley Trento Kassel Bologna – Term: node is responsible for item k 15 0 1 14 • Example – – H(“Anwitaman”)=12 H(“Ali”)=2 H(“Alberto”)=9 H(“Ozalp”)=14 2 13 3 12 4 5 11 6 10 9 8 7 16

Consistent Hashing: Summary • + Scalable – Each node stores avg D/n items (for D total items, n nodes) – Reshuffle on avg D/n items for every join/leave/failure • - However: global knowledge - everybody knows everybody – Akamai works this way – Amazon Dynamo too 15 0 1 14 • + Load balancing – w. h. p. O(log n) imbalance – Can eliminate imbalance by having each server ”simulate” log(n) random buckets 2 13 3 12 4 5 11 6 10 9 8 7 17

towards dht construction giving up on global knowledge 18

Where to point (Chord)? • Each node points to its successor – The successor of a node p is succ(p+1) – Known as a node’s succ pointer • Each node points to its predecessor – First node met in anti-clockwise direction starting at n-1 – Known as a node’s pred pointer 15 • Example – – – 0’s successor is succ(1)=2 2’s successor is succ(3)=5 5’s successor is succ(6)=6 6’s successor is succ(7)=11 11’s successor is succ(12)=0 0 1 14 2 13 3 12 4 5 11 6 10 9 8 7 19

DHT Lookup • To lookup a key k Key Anwitaman • H(”Alberto”)=9 • Traverse nodes: 2, 5, 6, 11 (BINGO) • Return “Trento” to initiator Trento Kurt Kassel Ozalp Bologna 15 • Example – Lookup ”Alberto” at node 2 Berkeley Alberto – Follow succ pointers until item k is found Singapore Ali – Calculate H(k) Value 0 1 14 2 13 3 12 4 5 11 6 10 9 8 7 20

towards dht construction handling joins/leaves/failures 21

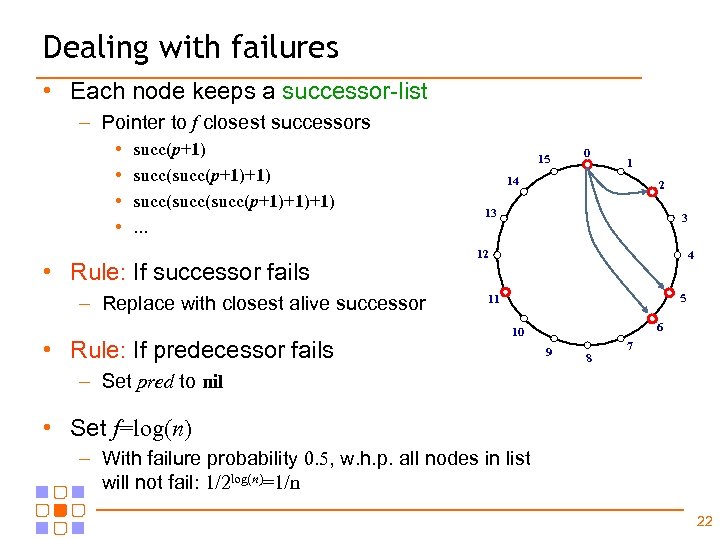
Dealing with failures • Each node keeps a successor-list – Pointer to f closest successors • • succ(p+1)+1) succ(succ(p+1)+1)+1). . . • Rule: If successor fails – Replace with closest alive successor • Rule: If predecessor fails 15 0 1 14 2 13 3 12 4 5 11 6 10 9 8 7 – Set pred to nil • Set f=log(n) – With failure probability 0. 5, w. h. p. all nodes in list will not fail: 1/2 log(n)=1/n 22

Handling Dynamism • Periodic stabilization used to make pointers eventually correct – Try pointing succ to closest alive successor – Try pointing pred to closest alive predecessor Periodically at node p: When receiving notify(q) at node p: 1. 2. 3. 4. 1. 2. set v: =succ. pred if v≠nil and v is in (p, succ] set succ: =v send a notify(p) to succ if pred=nil or q is in (pred, p] set pred: =q 23

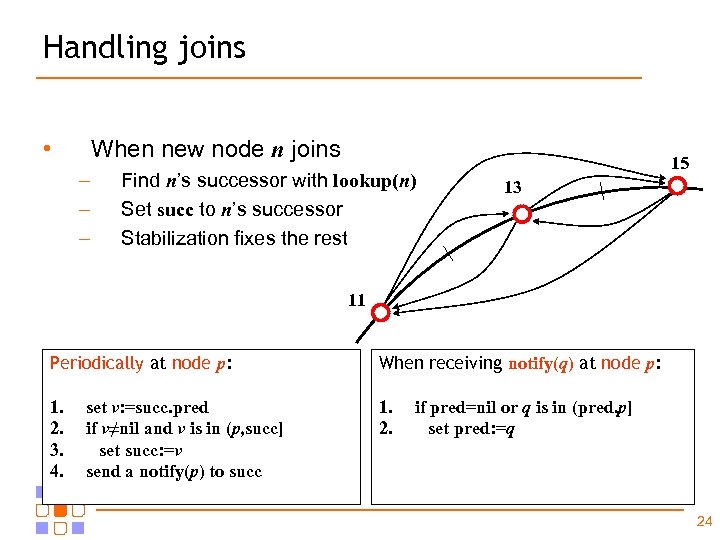
Handling joins • When new node n joins – – – Find n’s successor with lookup(n) Set succ to n’s successor Stabilization fixes the rest 15 13 11 Periodically at node p: When receiving notify(q) at node p: 1. 2. 3. 4. 1. 2. set v: =succ. pred if v≠nil and v is in (p, succ] set succ: =v send a notify(p) to succ if pred=nil or q is in (pred, p] set pred: =q 24

Handling leaves • When n leaves – • Just dissappear (like failure) 15 When pred detected failed – • 13 Set pred to nil When succ detected failed – Set succ to closest alive in successor list 11 Periodically at node p: When receiving notify(q) at node p: 1. 2. 3. 4. 1. 2. set v: =succ. pred if v≠nil and v is in (p, succ] set succ: =v send a notify(p) to succ if pred=nil or q is in (pred, p] set pred: =q 25

Speeding up lookups with fingers • If only pointer to succ(p+1) is used – • Improving lookup time (binary search) – – – • Worst case lookup time is n, for n nodes Point to succ(p+1) Point to succ(p+2) Point to succ(p+4) Point to succ(p+8) … Point to succ(p+2(log N)-1) 15 0 1 14 2 13 3 12 Distance always halved to the destination, log hops 4 5 11 6 10 9 8 7 26

Handling Dynamism of Fingers and SList • Node p periodically: – Update fingers • Lookup p+21, p+22, p+23, …, p+2(log N)-1 – Update successor-list • slist : = trunc(succ · succ. slist) 27

Chord: Summary • Lookup hops is logarithmic in n – Fast routing/lookup like in a dictionary • Routing table size is logarithmic in n – Few nodes to ping 28

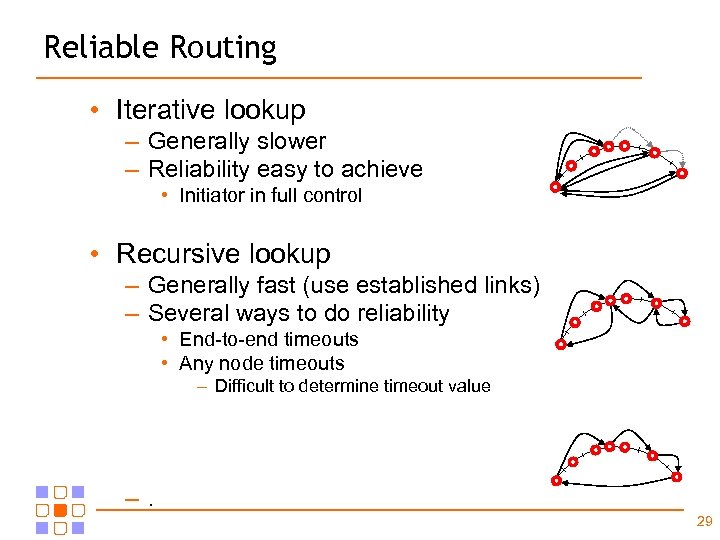
Reliable Routing • Iterative lookup – Generally slower – Reliability easy to achieve • Initiator in full control • Recursive lookup – Generally fast (use established links) – Several ways to do reliability • End-to-end timeouts • Any node timeouts – Difficult to determine timeout value –. 29

Replication of items • Successor-list replication (most systems) – Idea: replicate nodes • If node p responsible for set of items K • Replicate K on p’s immediate successors • Symmetric Replication – Idea: replicate identifiers • • Items with key 0, 16, 32, 48 equivalent Whoever is responsible for 0, also stores 16, 32, 48 Whoever is responsible for 16, also stores 0, 32, 48 … 30

towards proximity awareness plaxton-mesh (PRR) pastry/tapestry 31

Plaxton Mesh [PRR] • Identifiers represented with radix/base k – Often k=16, hexadecimal radix – Ring size N is a large power of k, e. g. 1640 32

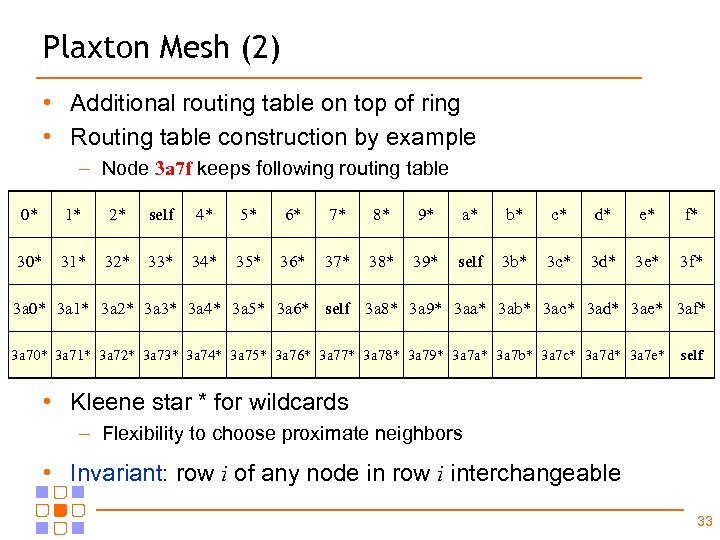
Plaxton Mesh (2) • Additional routing table on top of ring • Routing table construction by example – Node 3 a 7 f keeps following routing table 0* 1* 2* self 4* 5* 6* 7* 8* 9* a* b* c* d* e* f* 30* 31* 32* 33* 34* 35* 36* 37* 38* 39* self 3 b* 3 c* 3 d* 3 e* 3 f* 3 a 0* 3 a 1* 3 a 2* 3 a 3* 3 a 4* 3 a 5* 3 a 6* self 3 a 8* 3 a 9* 3 aa* 3 ab* 3 ac* 3 ad* 3 ae* 3 af* 3 a 70* 3 a 71* 3 a 72* 3 a 73* 3 a 74* 3 a 75* 3 a 76* 3 a 77* 3 a 78* 3 a 79* 3 a 7 a* 3 a 7 b* 3 a 7 c* 3 a 7 d* 3 a 7 e* self • Kleene star * for wildcards – Flexibility to choose proximate neighbors • Invariant: row i of any node in row i interchangeable 33

Plaxton Routing • To route from 1234 to abcd: 1. 2. 3. 4. • 1234 uses rt row 1: jump to a*, eg a 999 uses rt row 2: jump to ab*, eg ab 11 uses rt row 3: jump to abc*, eg abc 0 uses rt row 4: jump to abcd Routing terminates in log(N) hops – In practise log(n), where N is id size and n is number of nodes 34

Pastry – extension to Plaxton mesh • Leaf set – – • Successor-list in both directions Periodically gossiped to all leafs O(n 2) [Bamboo] Plaxton-mesh on top of ring – Failures in routing table • • Get replacement from any node on same row Routing 1) Route directly to responsible node in leaf set, otherwise 2) Route to closer (prefix) node, otherwise 3) Route on ring 35

architecture of structured overlays a formal view of DHTs 36

General Architecture for DHTs • Metric space S with distance function d – – – d(x, y)≥ 0 d(x, x)=0 d(x, y)=0 x=y d(x, y) + d(y, z) ≤ d(x, z) d(x, y)=d(y, x) (not always in reality) • Eg: – d(x, y) = y – x (mod N) – d(x, y) = x xor y – d(x, y) = sqrt( (x 1 -y 1)2 + … + (xd-yd)2 ) Chord Kademlia CAN 37

Graph Embedding • Embed a virtual graph for routing – – Powers of 2 (Chord) Plaxton mesh (Pastry/Tapestry) Hypercube Butterfly (Viceroy) • A node responsible for many virtual identifiers (keys) – Eg Chord nodes responsible for all virtual ids between node id and predecessor 38

XOR routing 39

numerous optimizations 40

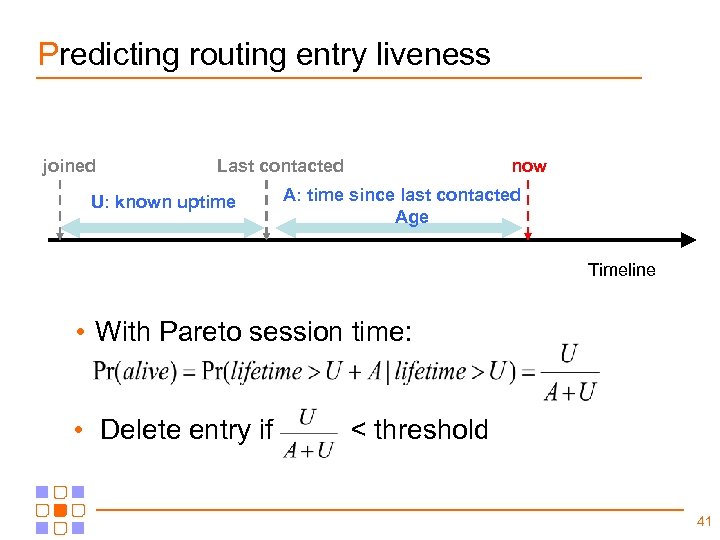
Predicting routing entry liveness joined Last contacted U: known uptime now A: time since last contacted Age Timeline • With Pareto session time: • Delete entry if < threshold 41

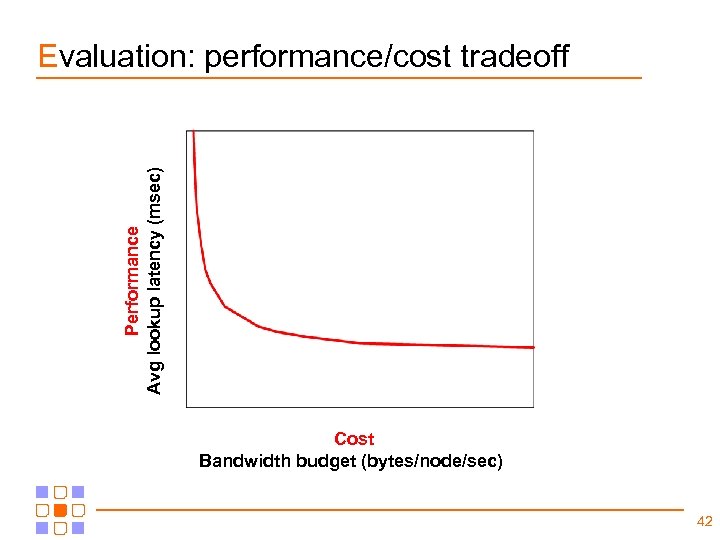
Performance Avg lookup latency (msec) Evaluation: performance/cost tradeoff Cost Bandwidth budget (bytes/node/sec) 42

Avg lookup latency (msec) Comparing with parameterized DHTs Avg bandwidth consumed (bytes/node/sec) 43

Avg Lookup latency (msec) Convex hull outlines best tradeoffs Avg bandwidth consumed (bytes/node/sec) 44

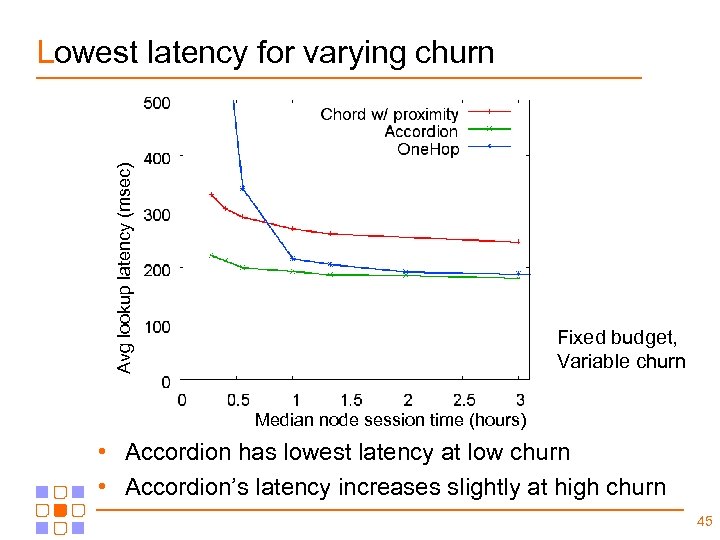
Avg lookup latency (msec) Lowest latency for varying churn Fixed budget, Variable churn Median node session time (hours) • Accordion has lowest latency at low churn • Accordion’s latency increases slightly at high churn 45

Avg bandwidth (bytes/node/sec) Accordion stays within budget Fixed budget, Variable churn Median node session time (hours) • Other protocols’ bandwidth increases with churn 46

DHTs • Characteristic property – Self-manage responsibilities in presence: • • • Node joins Node leaves Node failures Load-imbalance Replicas • Basic structure of DHTs – Metric space – Embed graph with efficient search algo – Let each node simulate many virtual nodes 47