STRUCTURE OF SOLIDS q Types of solids based

STRUCTURE OF SOLIDS q Types of solids based on structure q Types of solids based on bonding

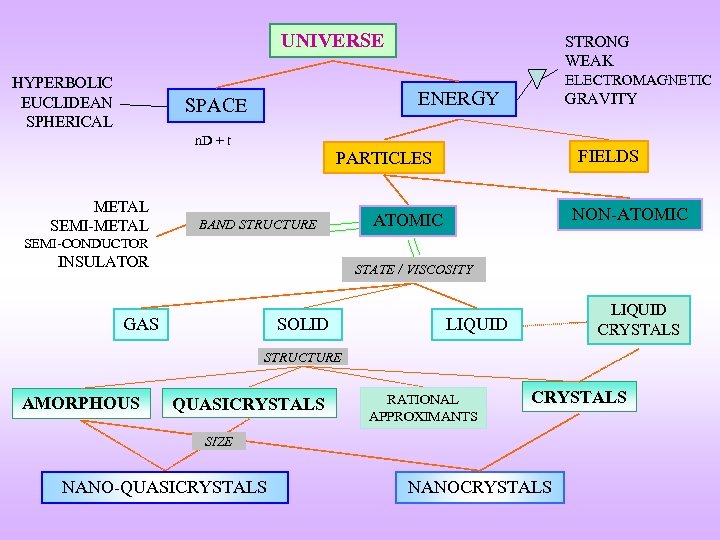
UNIVERSE HYPERBOLIC EUCLIDEAN SPHERICAL STRONG WEAK ELECTROMAGNETIC ENERGY SPACE GRAVITY n. D + t FIELDS PARTICLES METAL SEMI-METAL BAND STRUCTURE NON-ATOMIC SEMI-CONDUCTOR INSULATOR STATE / VISCOSITY GAS SOLID LIQUID CRYSTALS LIQUID STRUCTURE AMORPHOUS QUASICRYSTALS RATIONAL APPROXIMANTS CRYSTALS SIZE NANO-QUASICRYSTALS NANOCRYSTALS

CLASSIFICATION OF SOLIDS BASED ON ATOMIC ARRANGEMENT AMORPHOUS Ordered + Periodic QUASICRYSTALS Ordered + Periodic q There exists at least one crystalline state of lower energy (G) than the amorphous state (glass) q The crystal exhibits a sharp melting point q “Crystal has a higher density”!!

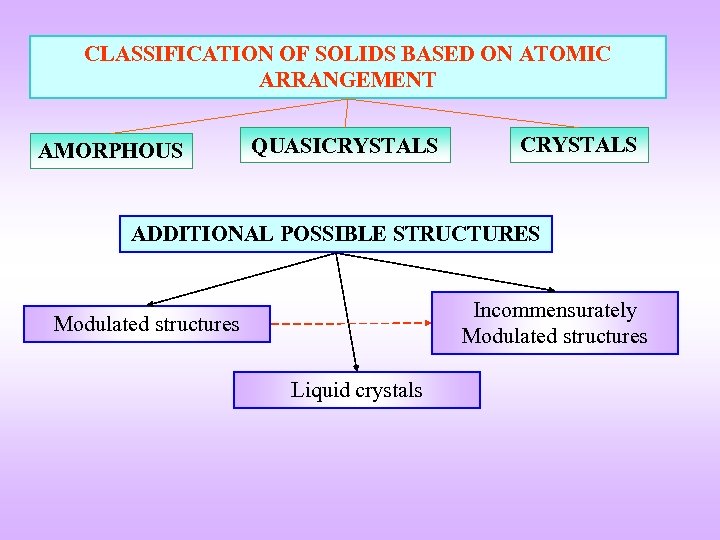
CLASSIFICATION OF SOLIDS BASED ON ATOMIC ARRANGEMENT AMORPHOUS QUASICRYSTALS ADDITIONAL POSSIBLE STRUCTURES Incommensurately Modulated structures Liquid crystals

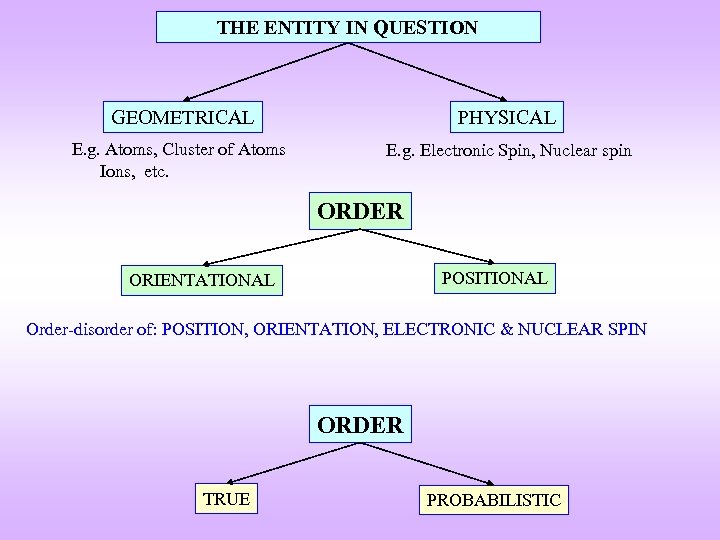
THE ENTITY IN QUESTION GEOMETRICAL PHYSICAL E. g. Atoms, Cluster of Atoms Ions, etc. E. g. Electronic Spin, Nuclear spin ORDER POSITIONAL ORIENTATIONAL Order-disorder of: POSITION, ORIENTATION, ELECTRONIC & NUCLEAR SPIN ORDER TRUE PROBABILISTIC

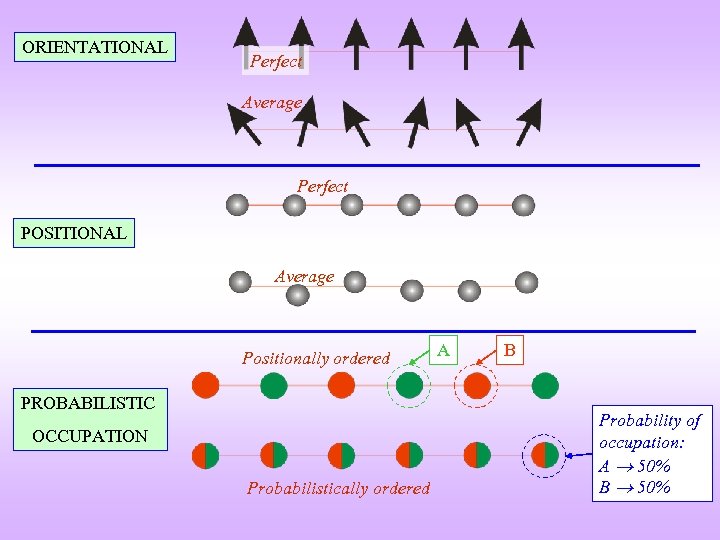
ORIENTATIONAL Perfect Average Perfect POSITIONAL Average Positionally ordered PROBABILISTIC OCCUPATION Probabilistically ordered A B Probability of occupation: A 50% B 50%

Order Spatial Temporal

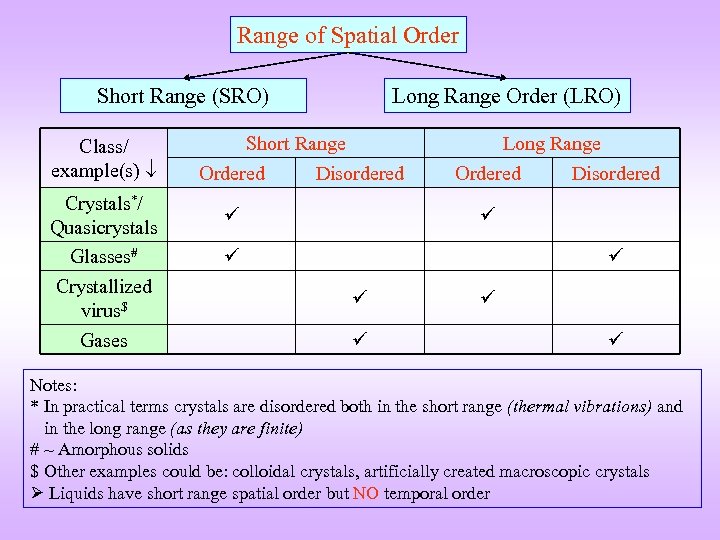
Range of Spatial Order Short Range (SRO) Class/ example(s) Crystals*/ Quasicrystals Glasses# Crystallized virus$ Gases Long Range Order (LRO) Short Range Ordered Disordered Long Range Ordered Disordered Notes: * In practical terms crystals are disordered both in the short range (thermal vibrations) and in the long range (as they are finite) # ~ Amorphous solids $ Other examples could be: colloidal crystals, artificially created macroscopic crystals Liquids have short range spatial order but NO temporal order

Crystal Physics, G. S. Zhdanov, Oliver & Boyd, Ediburgh, 1965

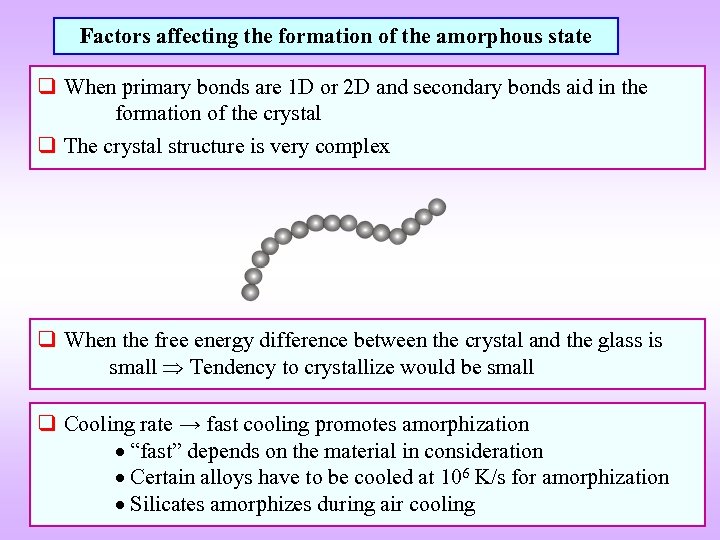
Factors affecting the formation of the amorphous state q When primary bonds are 1 D or 2 D and secondary bonds aid in the formation of the crystal q The crystal structure is very complex q When the free energy difference between the crystal and the glass is small Tendency to crystallize would be small q Cooling rate → fast cooling promotes amorphization “fast” depends on the material in consideration Certain alloys have to be cooled at 106 K/s for amorphization Silicates amorphizes during air cooling

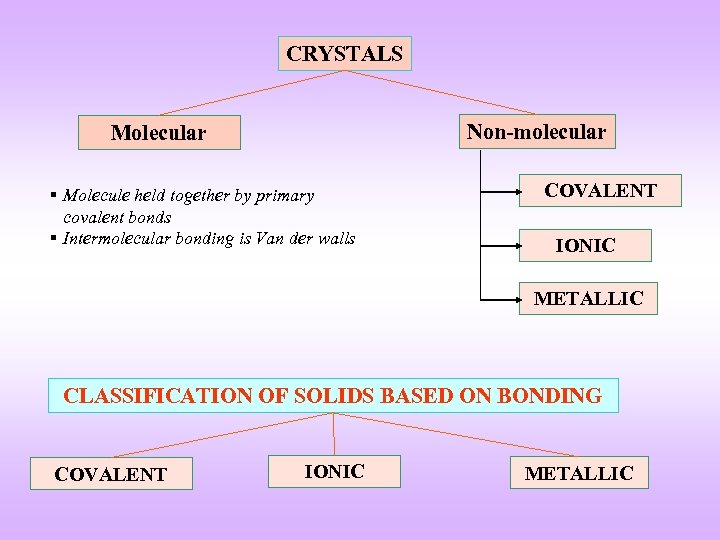
CRYSTALS Non-molecular Molecular § Molecule held together by primary covalent bonds § Intermolecular bonding is Van der walls COVALENT IONIC METALLIC CLASSIFICATION OF SOLIDS BASED ON BONDING COVALENT IONIC METALLIC

Approximate Strengths of Interactions between atoms Bond Type Covalent Bond k. J/mol 250 Electrostatic 5 van der Waals 5 Hydrogen bond 20

METALLIC q Positive ions in a free electron cloud q Metallic bonds are non-directional q Each atoms tends to surround itself with as many neighbours as possible! q Usually high temperature (wrt to MP) → BCC (Open structure) q The partial covalent character of transition metals is a possible reason for many of them having the BCC structure at low temperatures q FCC → Al, Fe (910 - 1410ºC), Cu, Ag, Au, Ni, Pd, Pt q BCC → Li, Na, K , Ti, Zr, Hf, Nb, Ta, Cr, Mo, W, Fe (below 910ºC), q HCP → Be, Mg, Ti, Zr, Hf, Zn, Cd q Others → La, Sm Po, α-Mn, Pu

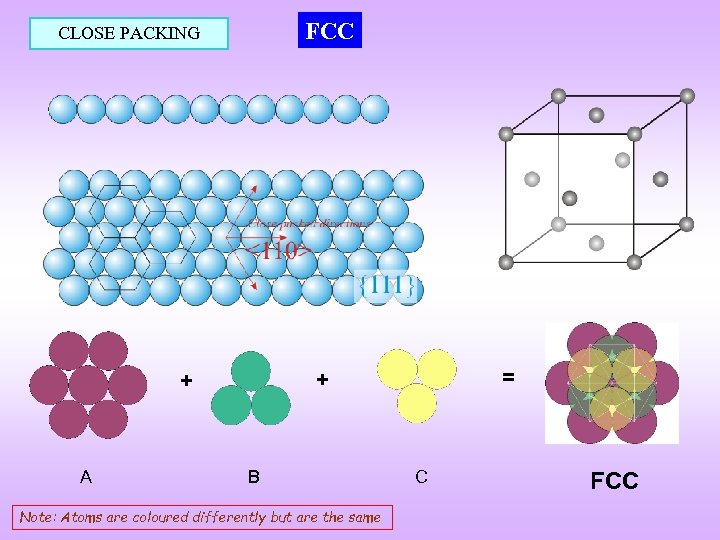
FCC CLOSE PACKING A = + + B Note: Atoms are coloured differently but are the same C FCC

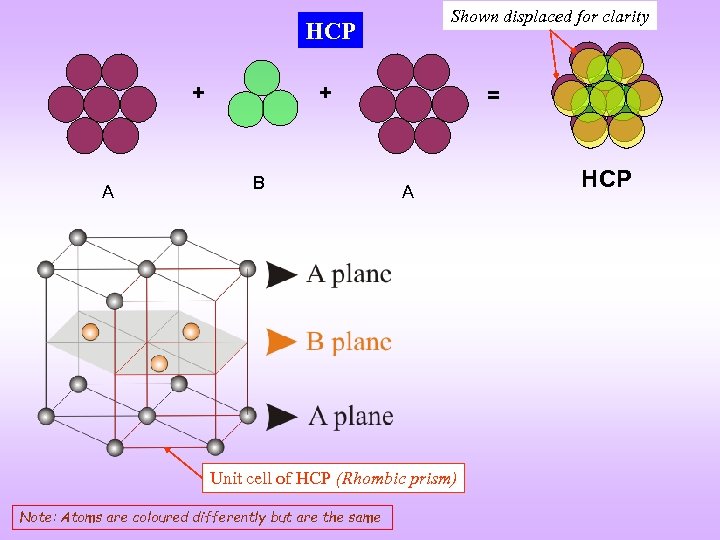
Shown displaced for clarity HCP + A + B = A Unit cell of HCP (Rhombic prism) Note: Atoms are coloured differently but are the same HCP

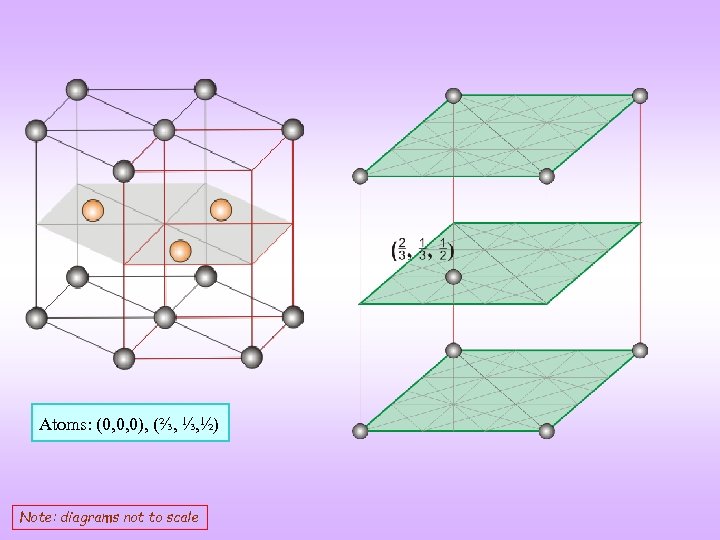
Atoms: (0, 0, 0), (⅔, ⅓, ½) Note: diagrams not to scale

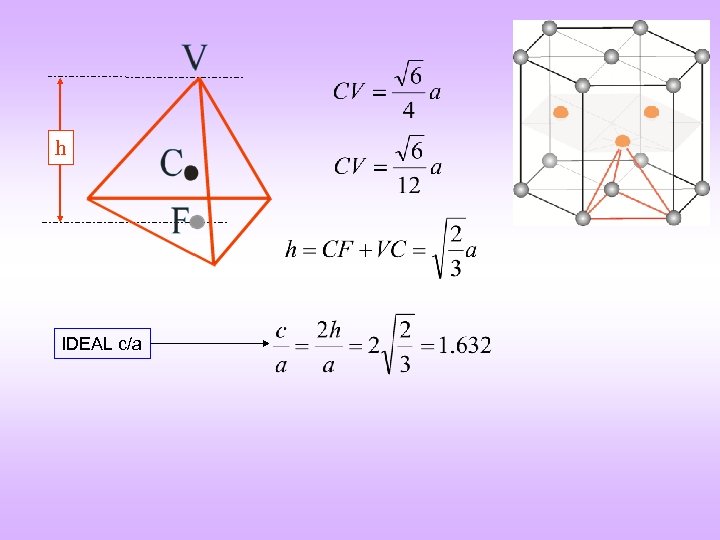
h IDEAL c/a

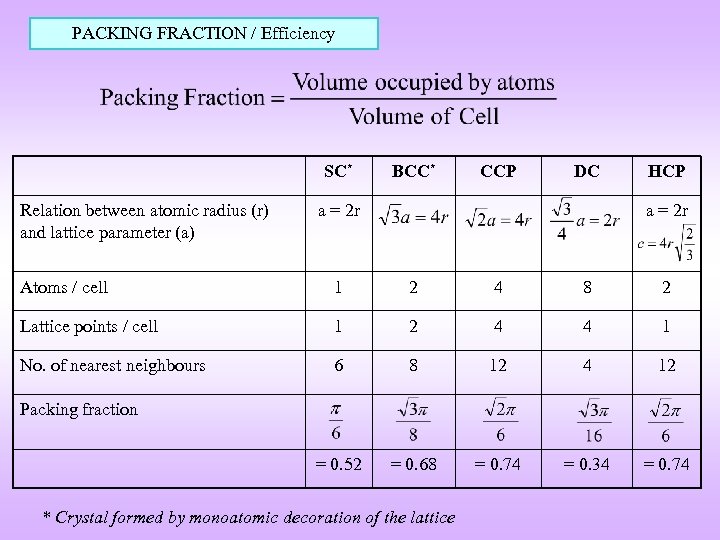
PACKING FRACTION / Efficiency SC* Relation between atomic radius (r) and lattice parameter (a) BCC* CCP DC a = 2 r HCP a = 2 r Atoms / cell 1 2 4 8 2 Lattice points / cell 1 2 4 4 1 No. of nearest neighbours 6 8 12 4 12 = 0. 52 = 0. 68 = 0. 74 = 0. 34 = 0. 74 Packing fraction * Crystal formed by monoatomic decoration of the lattice

ATOMIC DENSITY (atoms/unit area) SC (100) 1/a 2 = 1/a 2 FCC 2/a 2 (110) 1/(a 2 2) = 0. 707/a 2 2/a 2 BCC = 2/a 2 1/a 2 = 1. 414/a 2 2/a 2 = 1. 414/a 2 (111) 1/( 3 a 2) = 0. 577/a 2 4/( 3 a 2) = 2. 309/a 2 1/( 3 a 2) = 0. 577/a 2 Order (111) < (110) < (100) < (111) < (100) < (110)

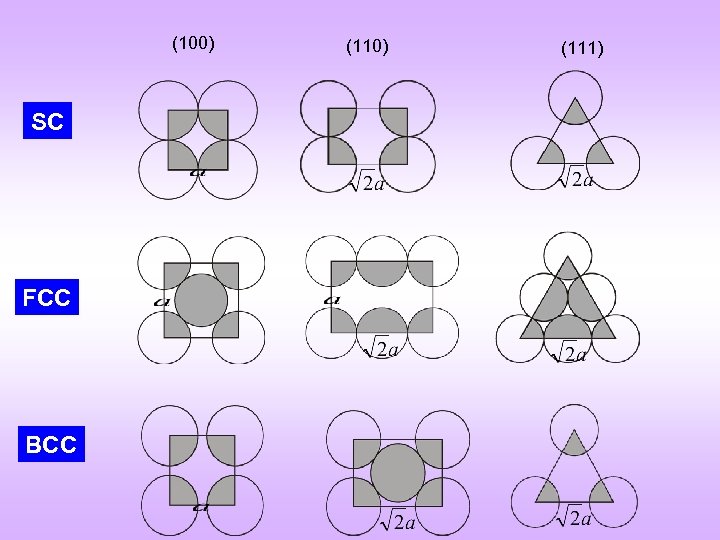
(100) SC FCC BCC (110) (111)

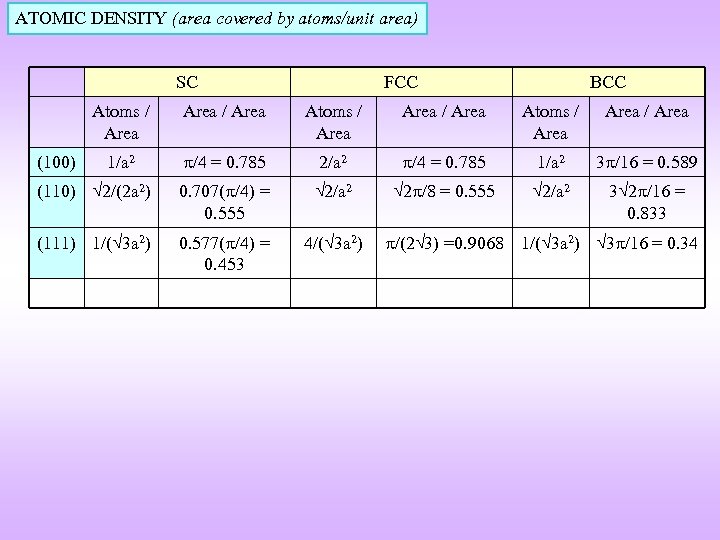
ATOMIC DENSITY (area covered by atoms/unit area) SC FCC BCC Atoms / Area / Area Atoms / Area 1/a 2 /4 = 0. 785 2/a 2 /4 = 0. 785 1/a 2 3 /16 = 0. 589 (110) 2/(2 a 2) 0. 707( /4) = 0. 555 2/a 2 2 /8 = 0. 555 2/a 2 3 2 /16 = 0. 833 (111) 1/( 3 a 2) 0. 577( /4) = 0. 453 4/( 3 a 2) (100) /(2 3) =0. 9068 1/( 3 a 2) 3 /16 = 0. 34

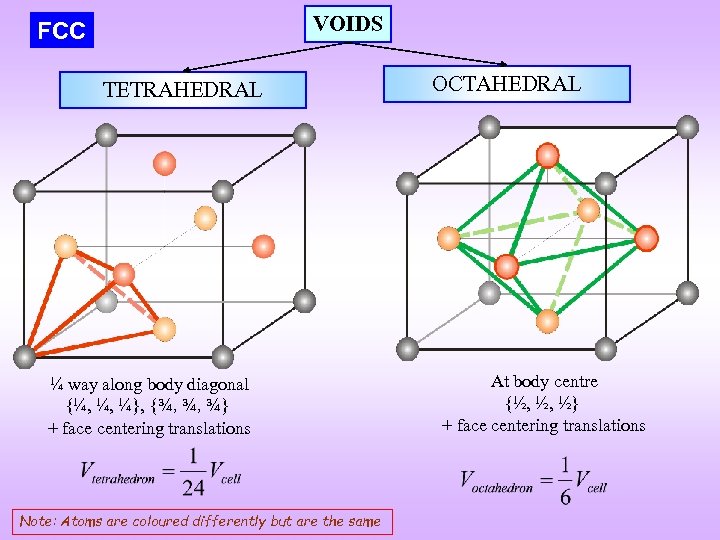
VOIDS FCC TETRAHEDRAL ¼ way along body diagonal {¼, ¼, ¼}, {¾, ¾, ¾} + face centering translations Note: Atoms are coloured differently but are the same OCTAHEDRAL At body centre {½, ½, ½} + face centering translations

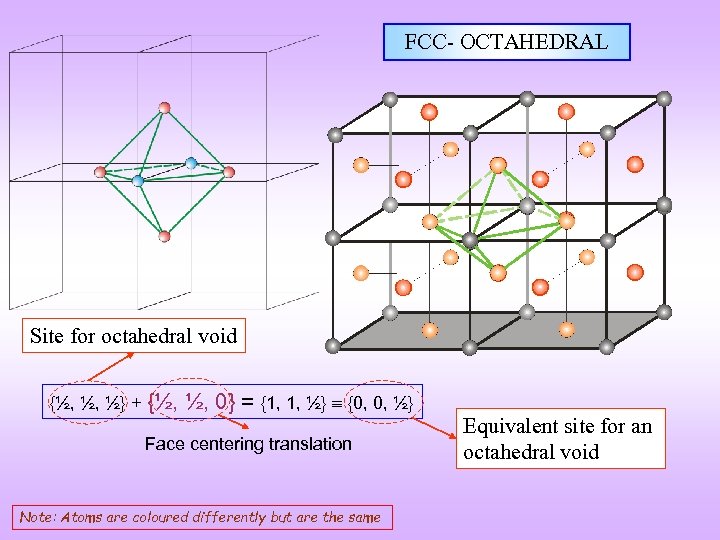
FCC- OCTAHEDRAL Site for octahedral void {½, ½, ½} + {½, ½, 0} = {1, 1, ½} {0, 0, ½} Face centering translation Note: Atoms are coloured differently but are the same Equivalent site for an octahedral void

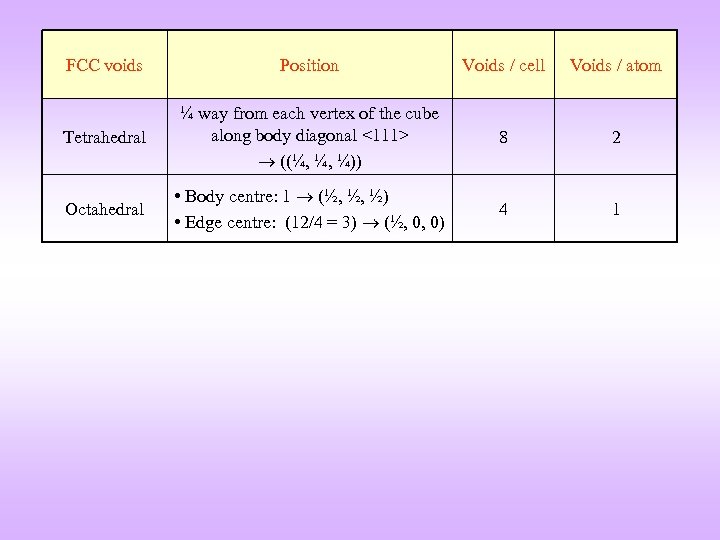
FCC voids Position Voids / cell Voids / atom Tetrahedral ¼ way from each vertex of the cube along body diagonal <111> ((¼, ¼, ¼)) 8 2 Octahedral • Body centre: 1 (½, ½, ½) • Edge centre: (12/4 = 3) (½, 0, 0) 4 1

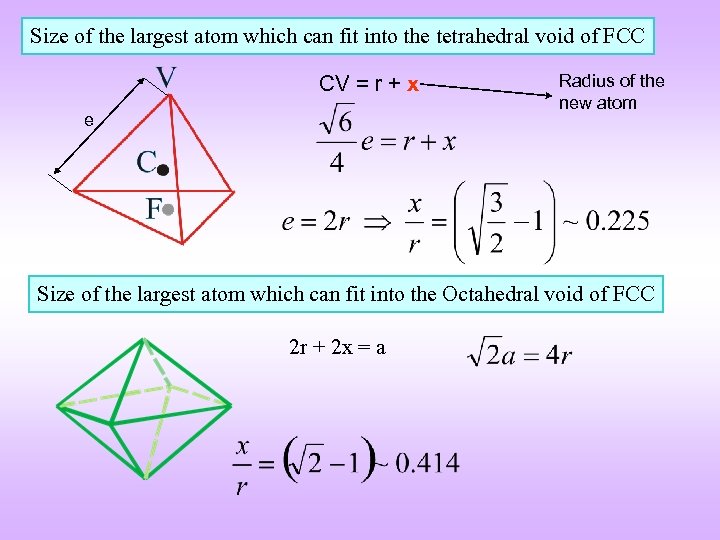
Size of the largest atom which can fit into the tetrahedral void of FCC CV = r + x e Radius of the new atom Size of the largest atom which can fit into the Octahedral void of FCC 2 r + 2 x = a

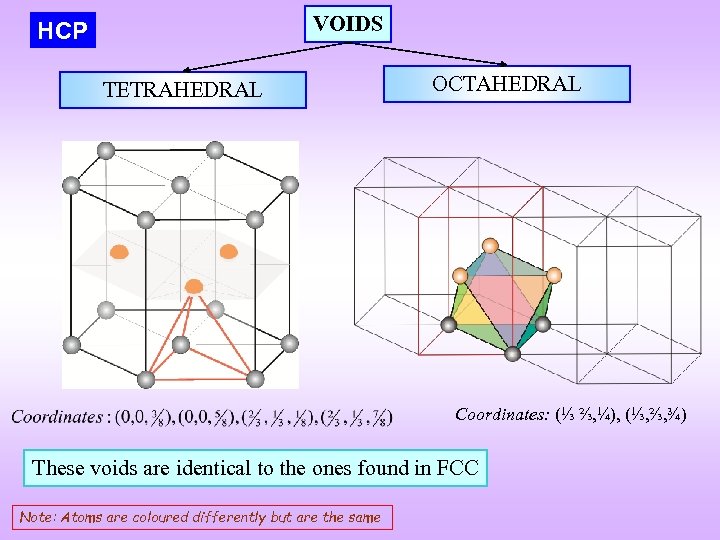
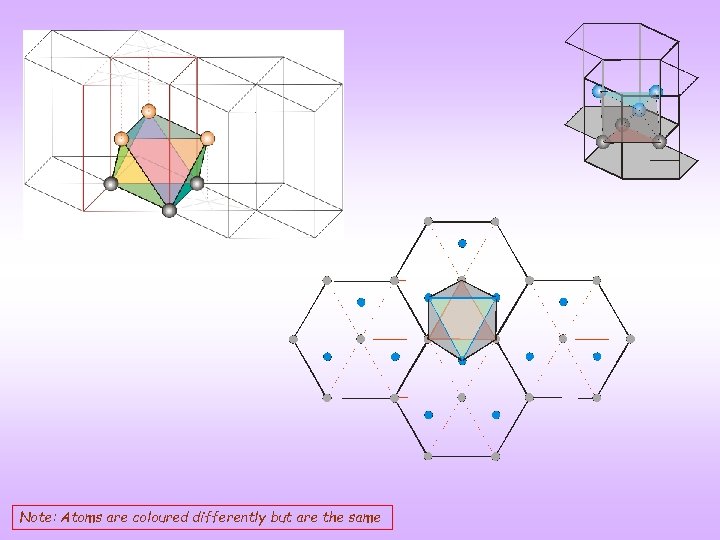
VOIDS HCP TETRAHEDRAL OCTAHEDRAL Coordinates: (⅓ ⅔, ¼), (⅓, ⅔, ¾) These voids are identical to the ones found in FCC Note: Atoms are coloured differently but are the same

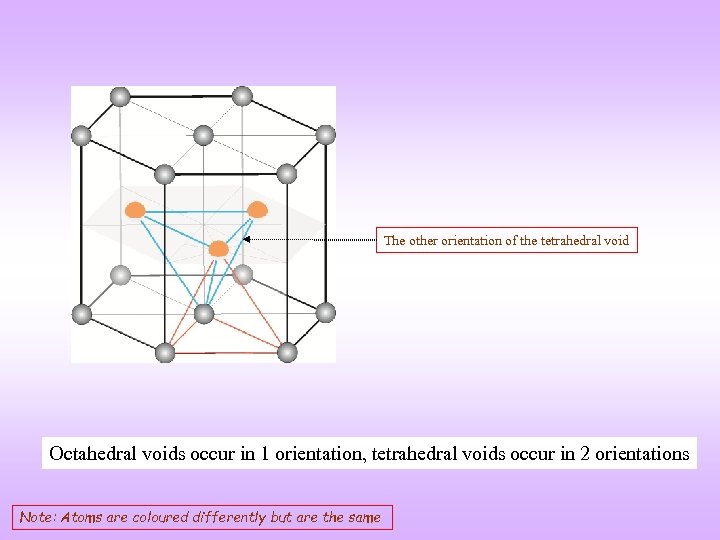
The other orientation of the tetrahedral void Octahedral voids occur in 1 orientation, tetrahedral voids occur in 2 orientations Note: Atoms are coloured differently but are the same

Note: Atoms are coloured differently but are the same

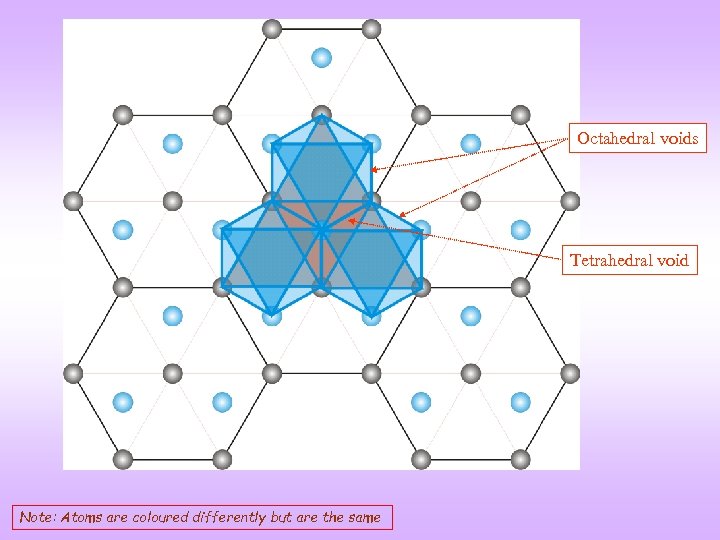
Octahedral voids Tetrahedral void Note: Atoms are coloured differently but are the same

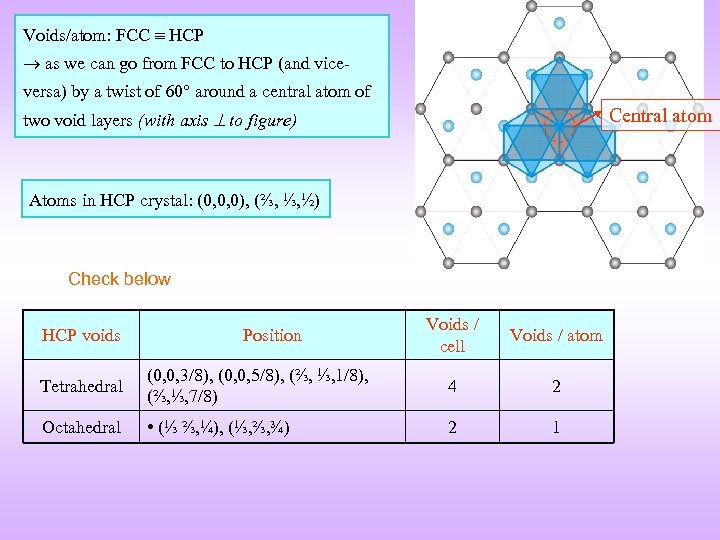
Voids/atom: FCC HCP as we can go from FCC to HCP (and viceversa) by a twist of 60 around a central atom of Central atom two void layers (with axis to figure) Atoms in HCP crystal: (0, 0, 0), (⅔, ⅓, ½) Check below HCP voids Position Voids / cell Voids / atom Tetrahedral (0, 0, 3/8), (0, 0, 5/8), (⅔, ⅓, 1/8), (⅔, ⅓, 7/8) 4 2 Octahedral • (⅓ ⅔, ¼), (⅓, ⅔, ¾) 2 1

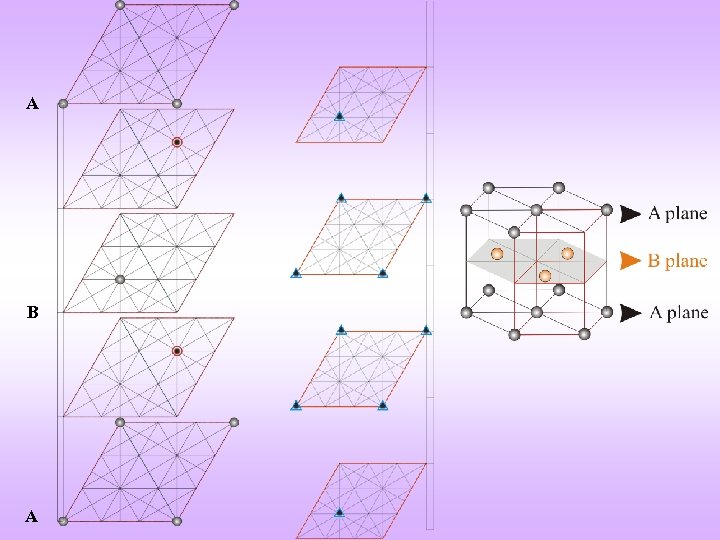
A B A

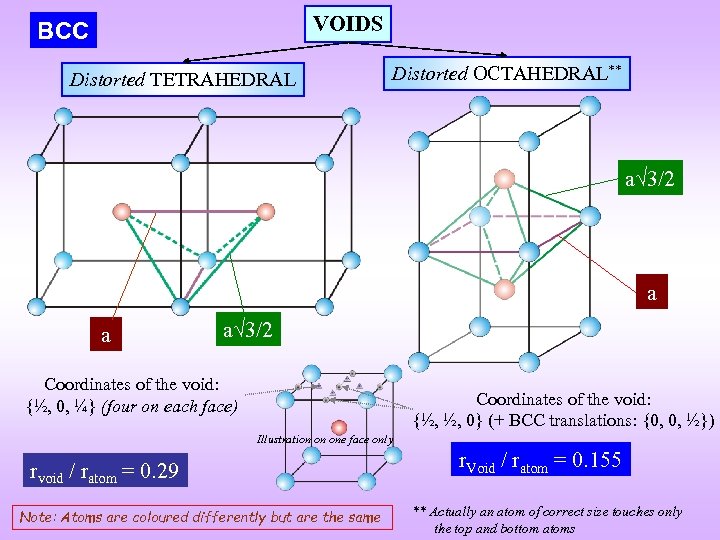
VOIDS BCC Distorted TETRAHEDRAL Distorted OCTAHEDRAL** a 3/2 a a a 3/2 Coordinates of the void: {½, 0, ¼} (four on each face) Coordinates of the void: {½, ½, 0} (+ BCC translations: {0, 0, ½}) Illustration on one face only rvoid / ratom = 0. 29 Note: Atoms are coloured differently but are the same r. Void / ratom = 0. 155 ** Actually an atom of correct size touches only the top and bottom atoms

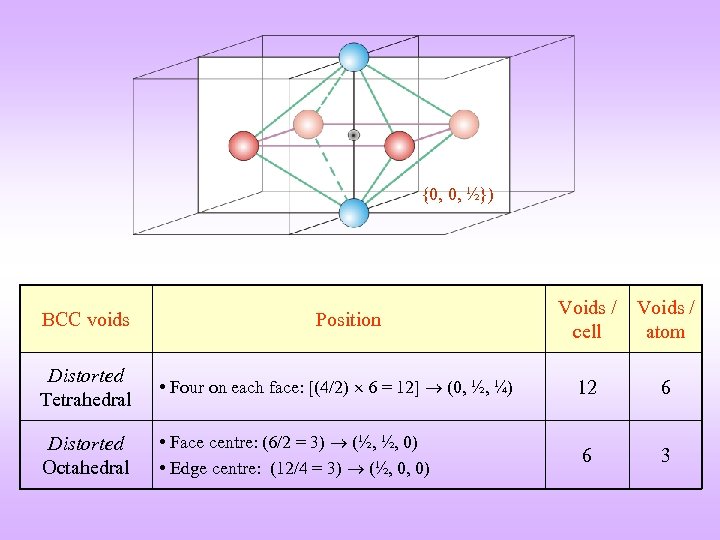
{0, 0, ½}) BCC voids Position Voids / cell Voids / atom Distorted Tetrahedral • Four on each face: [(4/2) 6 = 12] (0, ½, ¼) 12 6 Distorted Octahedral • Face centre: (6/2 = 3) (½, ½, 0) • Edge centre: (12/4 = 3) (½, 0, 0) 6 3

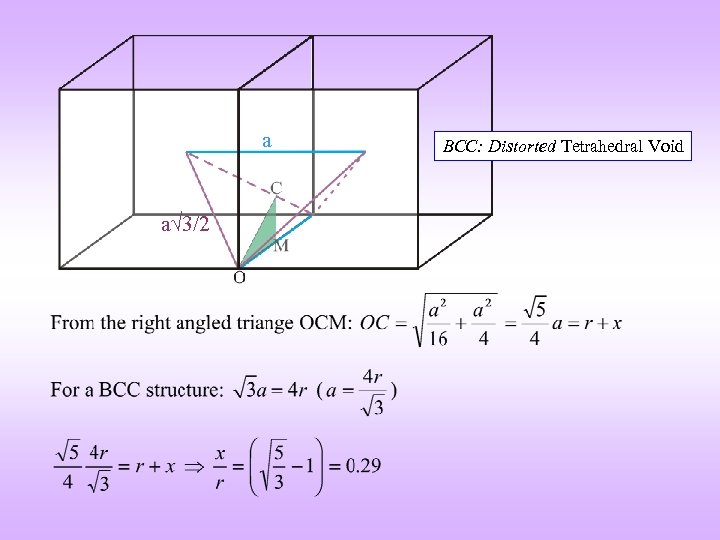
a a 3/2 BCC: Distorted Tetrahedral Void

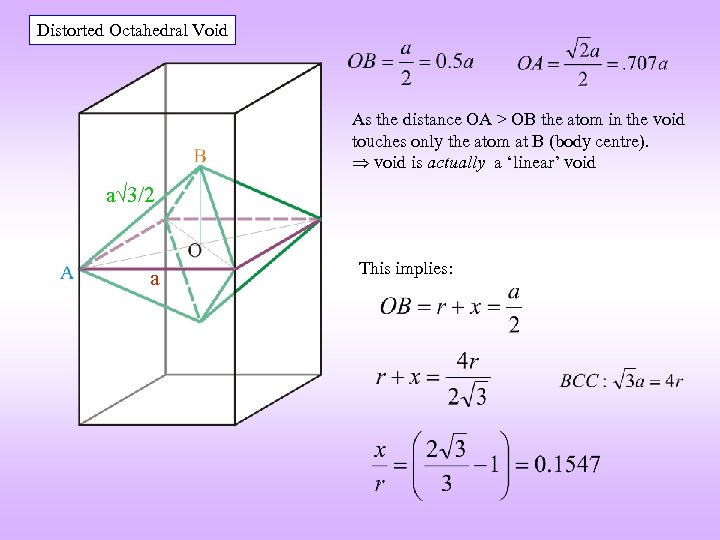
Distorted Octahedral Void As the distance OA > OB the atom in the void touches only the atom at B (body centre). void is actually a ‘linear’ void a 3/2 a This implies:

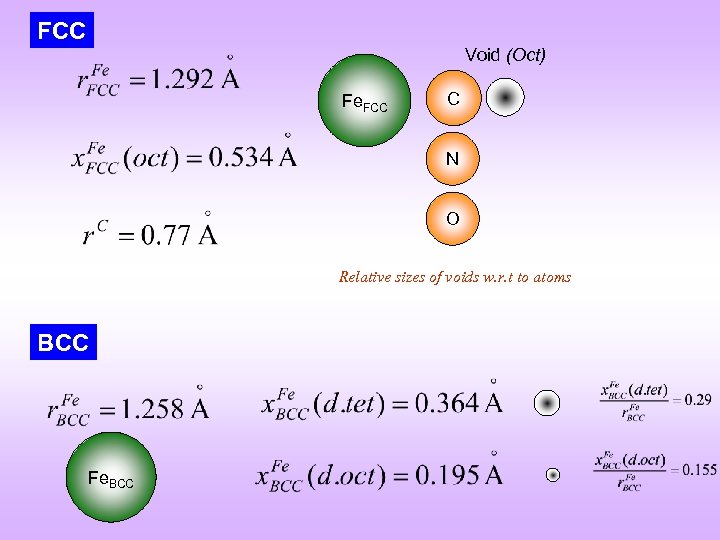
FCC Void (Oct) Fe. FCC C N O Relative sizes of voids w. r. t to atoms BCC Fe. BCC

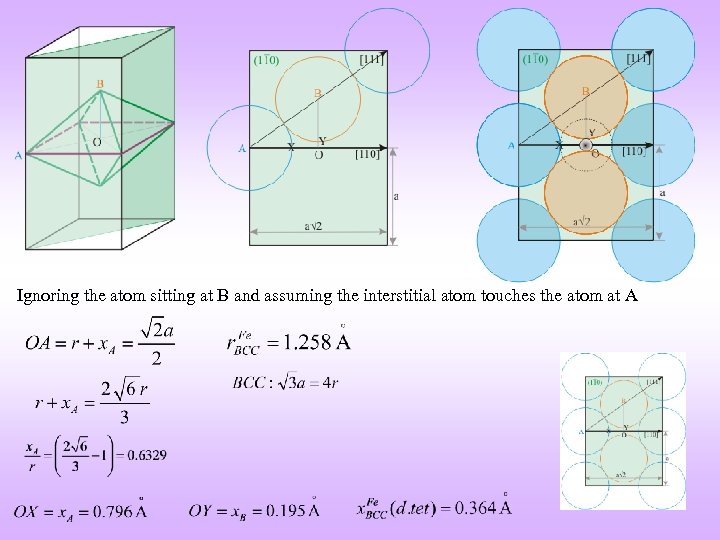
Ignoring the atom sitting at B and assuming the interstitial atom touches the atom at A

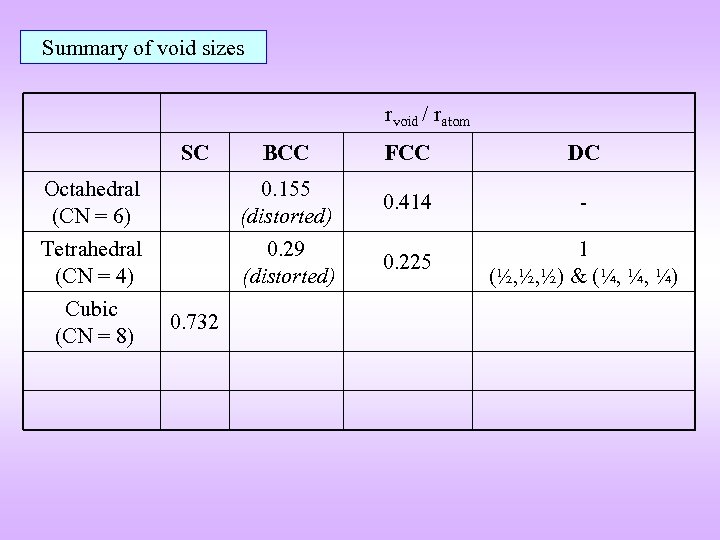
Summary of void sizes rvoid / ratom SC BCC FCC DC Octahedral (CN = 6) 0. 155 (distorted) 0. 414 - Tetrahedral (CN = 4) 0. 29 (distorted) 0. 225 1 (½, ½, ½) & (¼, ¼, ¼) Cubic (CN = 8) 0. 732

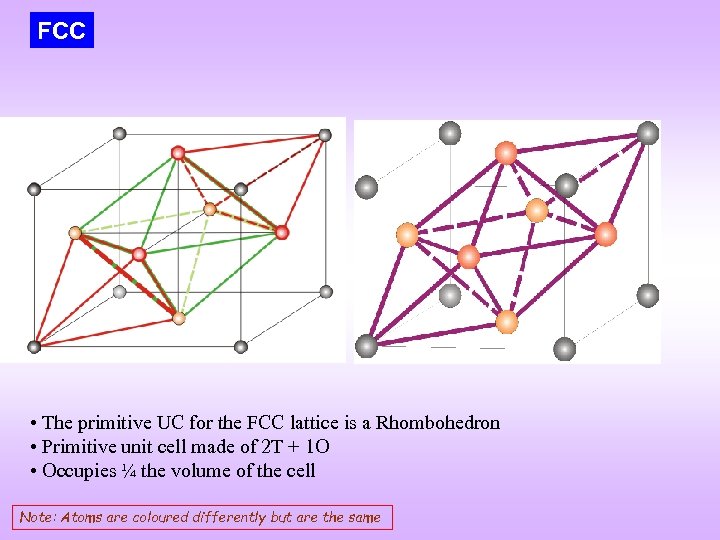
FCC • The primitive UC for the FCC lattice is a Rhombohedron • Primitive unit cell made of 2 T + 1 O • Occupies ¼ the volume of the cell Note: Atoms are coloured differently but are the same

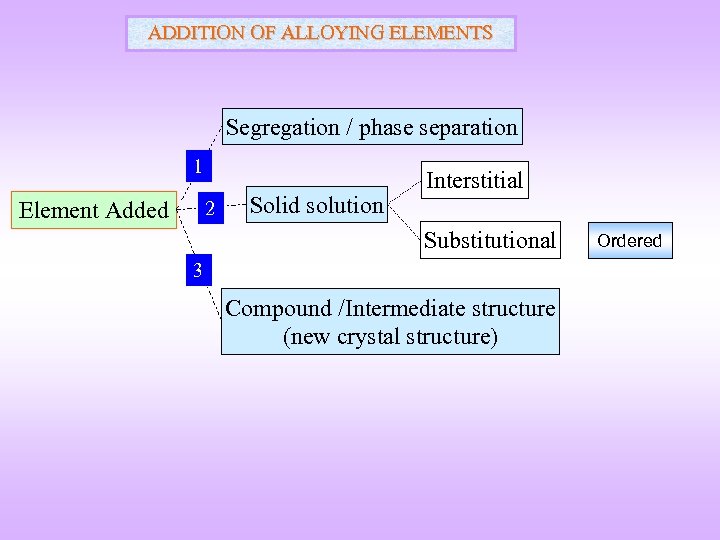
ADDITION OF ALLOYING ELEMENTS Segregation / phase separation 1 Element Added 2 Solid solution Interstitial Substitutional 3 Compound /Intermediate structure (new crystal structure) Ordered

1 Segregation / phase separation q The added element does not dissolve in the parent/matrix phase → in a polycrystal may go to the grain boundary

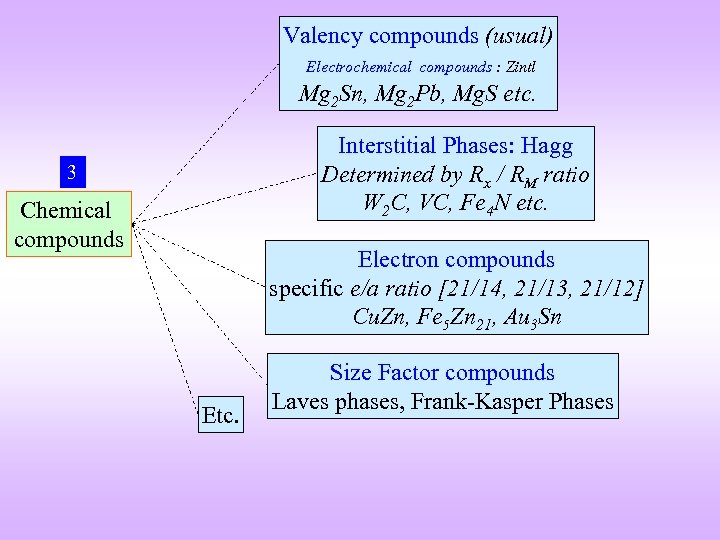
Valency compounds (usual) Electrochemical compounds : Zintl Mg 2 Sn, Mg 2 Pb, Mg. S etc. Interstitial Phases: Hagg Determined by Rx / RM ratio W 2 C, VC, Fe 4 N etc. 3 Chemical compounds Electron compounds specific e/a ratio [21/14, 21/13, 21/12] Cu. Zn, Fe 5 Zn 21, Au 3 Sn Etc. Size Factor compounds Laves phases, Frank-Kasper Phases

Zintl Phases: Chemical compounds Electrochemical compounds q Different crystal lattice as compared to the components q Each component has a specific location in the lattice q An. Bm q Different properties than components q Constant melting point and dissociation temperature q Accompanied by substantial thermal effect

2 Solid solution Substitutional Interstitial q The mixing is at the atomic scale and is analogous to a liquid solution NOTE q Pure components → A, B, C … q Solid solutions → , , … q Ordered Solid solutions → ’, ’ …

Substitutional Solid Solution HUME ROTHERY RULES Empirical rules for the formation of substitutional solid solution q The solute and solvent atoms do not differ by more than 15% in diameter q The electronegativity difference between the elements is small q The valency and crystal structure of the elements is same Additional rule q Element with higher valency is dissolved more in an element of lower valency rather than vice-versa

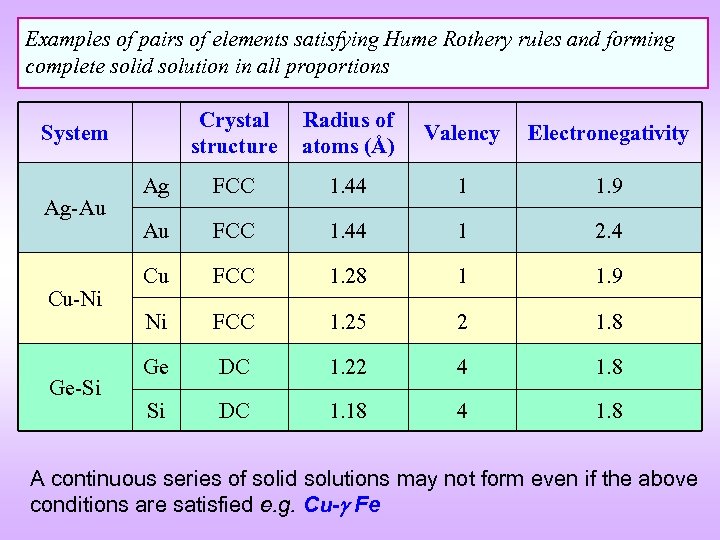
Examples of pairs of elements satisfying Hume Rothery rules and forming complete solid solution in all proportions Crystal structure Radius of atoms (Å) Valency Electronegativity Ag FCC 1. 44 1 1. 9 Au FCC 1. 44 1 2. 4 Cu FCC 1. 28 1 1. 9 Ni FCC 1. 25 2 1. 8 Ge DC 1. 22 4 1. 8 Si DC 1. 18 4 1. 8 System Ag-Au Cu-Ni Ge-Si A continuous series of solid solutions may not form even if the above conditions are satisfied e. g. Cu- Fe

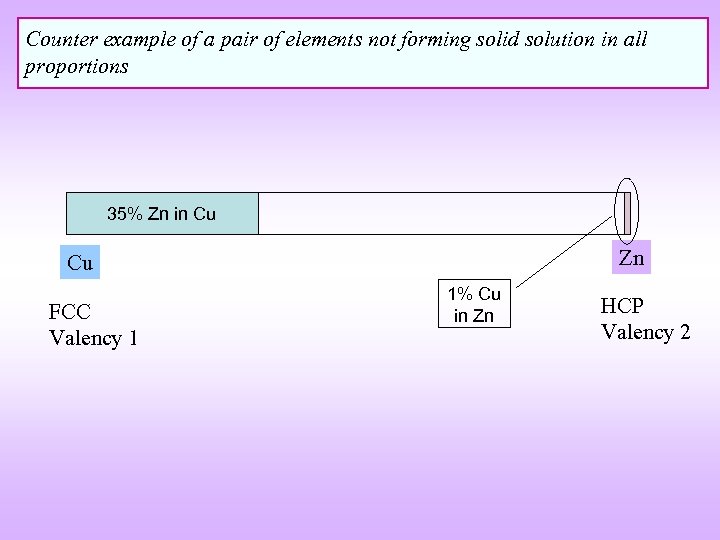
Counter example of a pair of elements not forming solid solution in all proportions 35% Zn in Cu Zn Cu FCC Valency 1 1% Cu in Zn HCP Valency 2

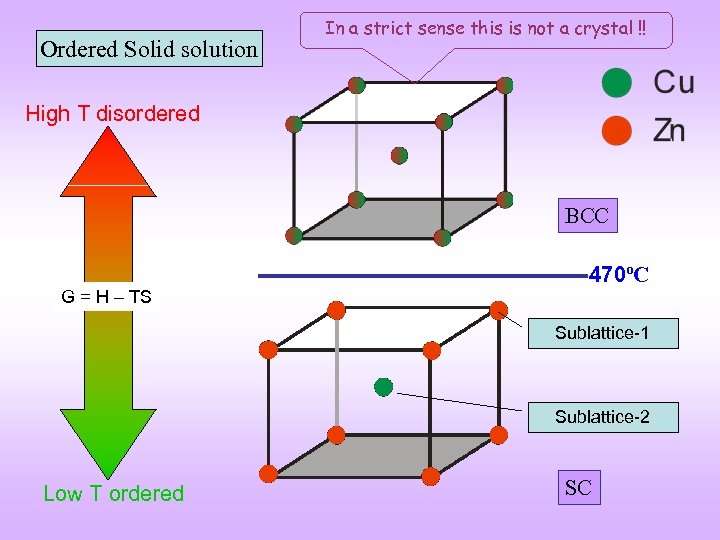
Ordered Solid solution In a strict sense this is not a crystal !! High T disordered BCC G = H TS 470ºC Sublattice-1 Sublattice-2 Low T ordered SC

ORDERING q A-B bonds are preferred to AA or BB bonds e. g. Cu-Zn bonds are preferred compared to Cu-Cu or Zn-Zn bonds q The ordered alloy in the Cu-Zn alloys is an example of an INTERMEDIATE STRUCTURE that forms in the system with limited solid solubility q The structure of the ordered alloy is different from that of both the component elements (Cu-FCC, Zn-HCP) q The formation of the ordered structure is accompanied by change in properties. E. g. in Permalloy ordering leads to → reduction in magnetic permeability, increase in hardness etc. [~Compound] q Complete solid solutions are formed when the ratios of the components of the alloy (atomic) are whole no. s → 1: 1, 1: 2, 1: 3 etc. [Cu. Au, Cu 3 Au. . ] q Ordered solid solutions are in-between solid solutions and chemical compounds q Degree of order decreases on heating and vanishes on reaching disordering temperature [ compound]

Interstitial Solid Solution q The second species added goes into the voids of the parent lattice q Octahedral and tetrahedral voids q E. g. C (r = 0. 77 Å), N (r = 0. 71 Å), H (r = 0. 46 Å)