382e342ee7447df8b9cc067bbc54c27c.ppt
- Количество слайдов: 25
 Strongly Interacting Low Viscosity Matter Created in Heavy Ion Collisions Joe Kapusta* University of Minnesota Quark Matter 2006, Shanghai, China * Original work done in collaboration with Laszlo Csernai and Larry Mc. Lerran.
Strongly Interacting Low Viscosity Matter Created in Heavy Ion Collisions Joe Kapusta* University of Minnesota Quark Matter 2006, Shanghai, China * Original work done in collaboration with Laszlo Csernai and Larry Mc. Lerran.
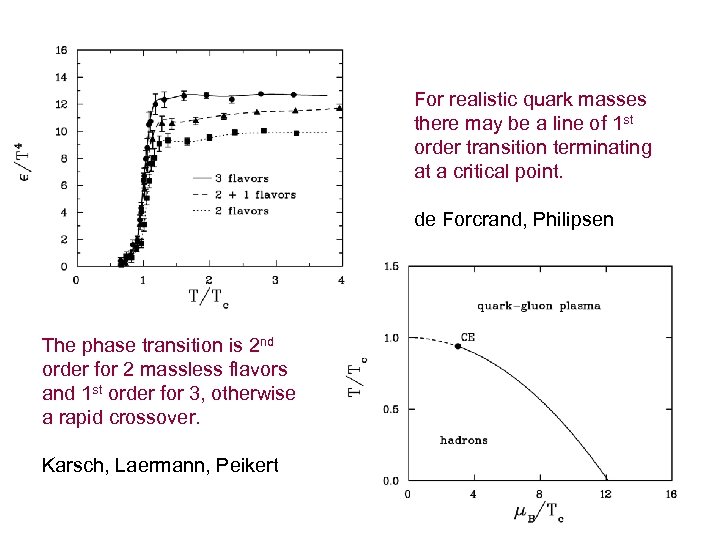 For realistic quark masses there may be a line of 1 st order transition terminating at a critical point. de Forcrand, Philipsen The phase transition is 2 nd order for 2 massless flavors and 1 st order for 3, otherwise a rapid crossover. Karsch, Laermann, Peikert
For realistic quark masses there may be a line of 1 st order transition terminating at a critical point. de Forcrand, Philipsen The phase transition is 2 nd order for 2 massless flavors and 1 st order for 3, otherwise a rapid crossover. Karsch, Laermann, Peikert
 What has RHIC told us about the equation of state?
What has RHIC told us about the equation of state?
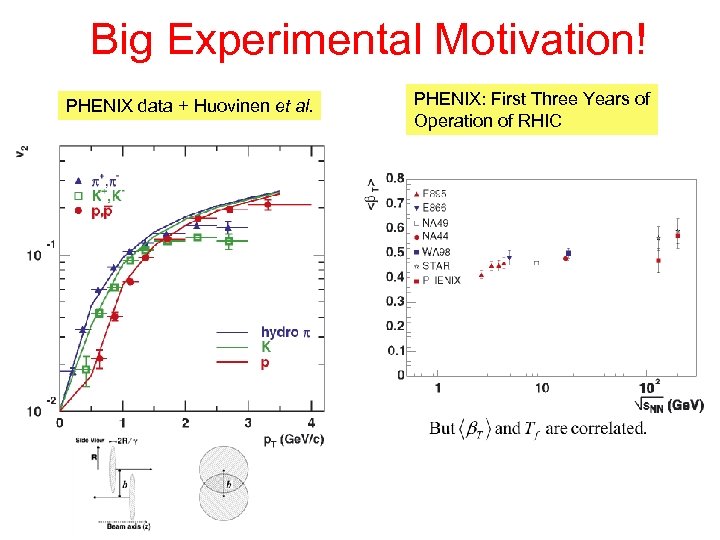 Big Experimental Motivation! PHENIX data + Huovinen et al. PHENIX: First Three Years of Operation of RHIC
Big Experimental Motivation! PHENIX data + Huovinen et al. PHENIX: First Three Years of Operation of RHIC
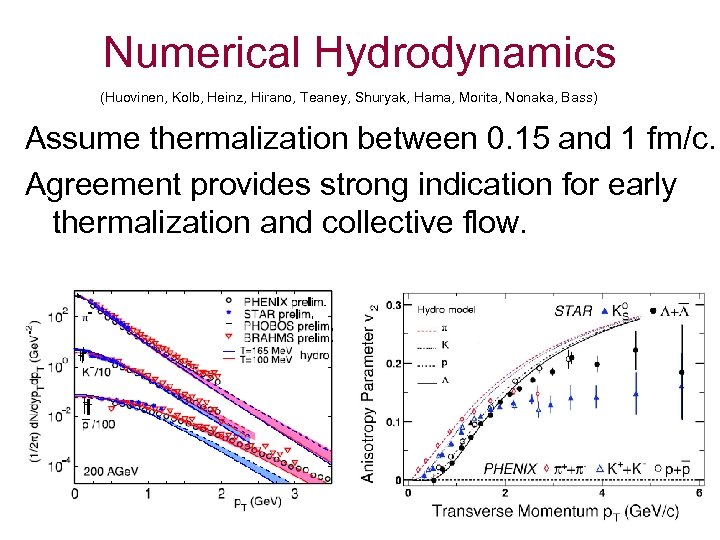 Numerical Hydrodynamics (Huovinen, Kolb, Heinz, Hirano, Teaney, Shuryak, Hama, Morita, Nonaka, Bass) Assume thermalization between 0. 15 and 1 fm/c. Agreement provides strong indication for early thermalization and collective flow.
Numerical Hydrodynamics (Huovinen, Kolb, Heinz, Hirano, Teaney, Shuryak, Hama, Morita, Nonaka, Bass) Assume thermalization between 0. 15 and 1 fm/c. Agreement provides strong indication for early thermalization and collective flow.
 Big Theoretical Motivation! Viscosity in Strongly Interacting Quantum Field Theories from Black Hole Physics Kovtun, Son, Starinets PRL 94, 111601 (2005) Using the Kubo formula the low energy absorption cross section for gravitons on black holes, and the black hole entropy formula they found that and conjectured that this is a universal lower bound.
Big Theoretical Motivation! Viscosity in Strongly Interacting Quantum Field Theories from Black Hole Physics Kovtun, Son, Starinets PRL 94, 111601 (2005) Using the Kubo formula the low energy absorption cross section for gravitons on black holes, and the black hole entropy formula they found that and conjectured that this is a universal lower bound.
 Is the RHIC data, in the form of elliptic and radial flow, telling us that the matter has very small viscosity, a perfect fluid ?
Is the RHIC data, in the form of elliptic and radial flow, telling us that the matter has very small viscosity, a perfect fluid ?
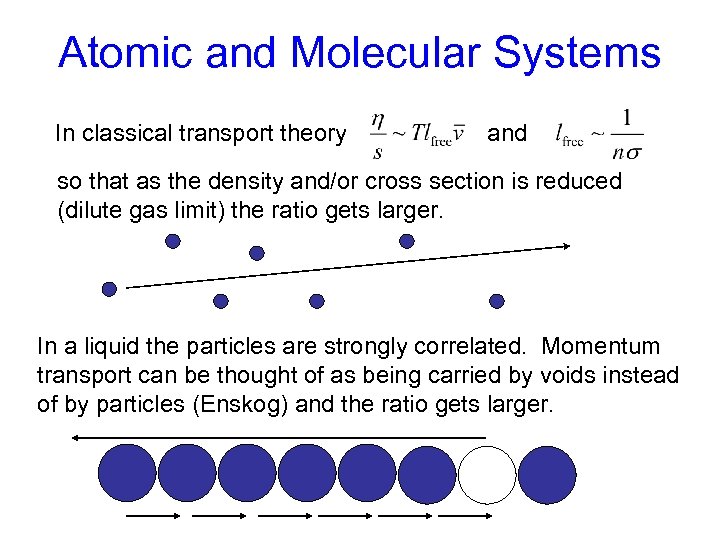 Atomic and Molecular Systems In classical transport theory and so that as the density and/or cross section is reduced (dilute gas limit) the ratio gets larger. In a liquid the particles are strongly correlated. Momentum transport can be thought of as being carried by voids instead of by particles (Enskog) and the ratio gets larger.
Atomic and Molecular Systems In classical transport theory and so that as the density and/or cross section is reduced (dilute gas limit) the ratio gets larger. In a liquid the particles are strongly correlated. Momentum transport can be thought of as being carried by voids instead of by particles (Enskog) and the ratio gets larger.
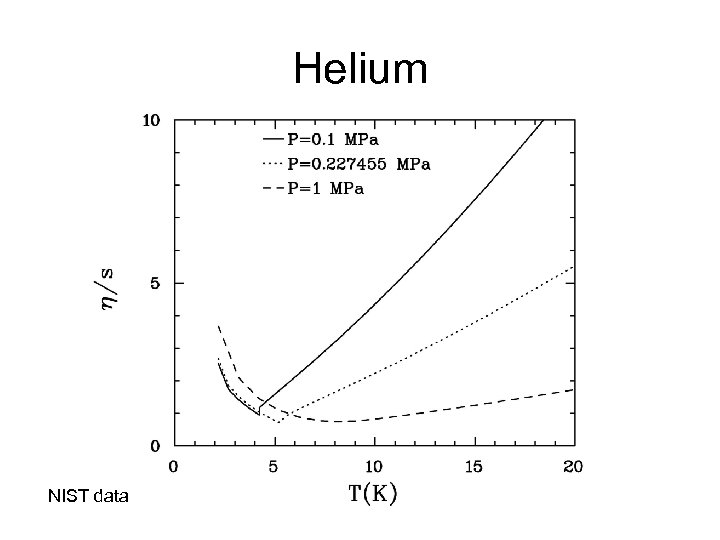 Helium NIST data
Helium NIST data
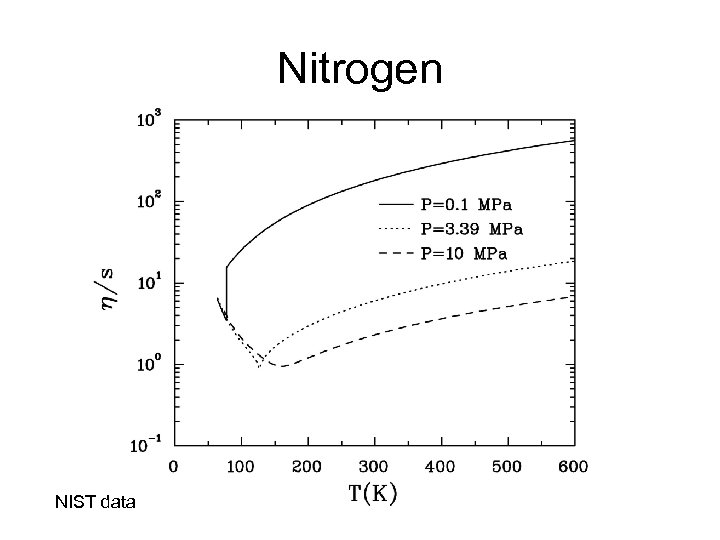 Nitrogen NIST data
Nitrogen NIST data
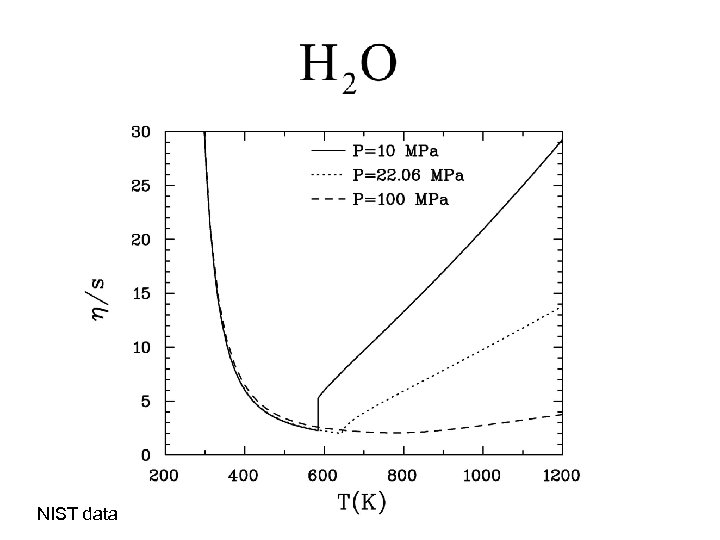 NIST data
NIST data
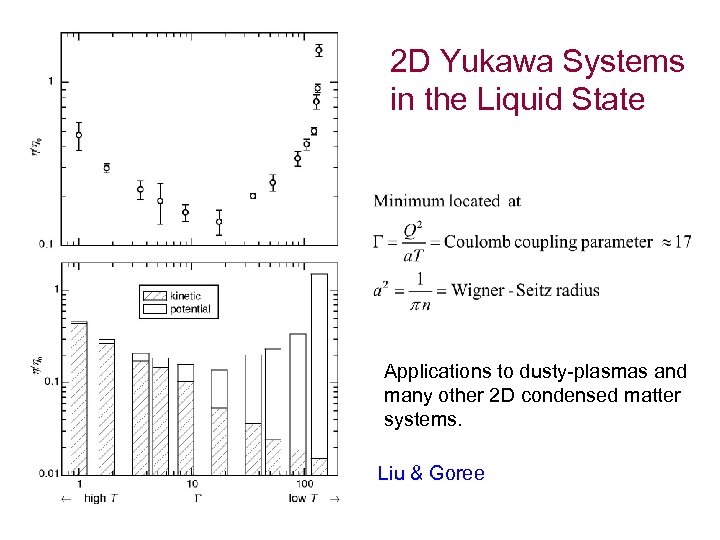 2 D Yukawa Systems in the Liquid State Applications to dusty-plasmas and many other 2 D condensed matter systems. Liu & Goree
2 D Yukawa Systems in the Liquid State Applications to dusty-plasmas and many other 2 D condensed matter systems. Liu & Goree
 QCD • Chiral perturbation theory at low T (Prakash et al. ): grows with decreasing T. • Quark-gluon plasma at high T (Arnold, Moore, Yaffe): grows with increasing T.
QCD • Chiral perturbation theory at low T (Prakash et al. ): grows with decreasing T. • Quark-gluon plasma at high T (Arnold, Moore, Yaffe): grows with increasing T.
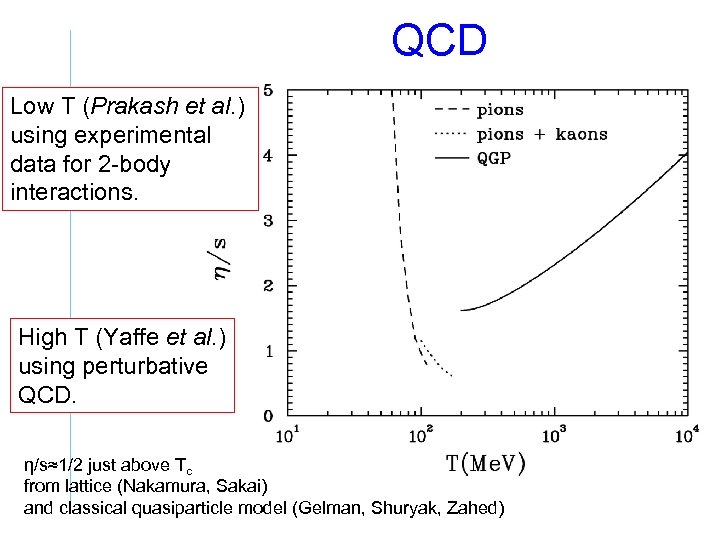 QCD Low T (Prakash et al. ) using experimental data for 2 -body interactions. High T (Yaffe et al. ) using perturbative QCD. η/s≈1/2 just above Tc from lattice (Nakamura, Sakai) and classical quasiparticle model (Gelman, Shuryak, Zahed)
QCD Low T (Prakash et al. ) using experimental data for 2 -body interactions. High T (Yaffe et al. ) using perturbative QCD. η/s≈1/2 just above Tc from lattice (Nakamura, Sakai) and classical quasiparticle model (Gelman, Shuryak, Zahed)
 Large Nc Limit at Low T • Baryon masses are proportional to Nc and can be neglected, meson masses are essentially independent of Nc. Hagedorn temperature and critical temperature should not change by much. Meson-meson cross sections scale as 1/ Nc 2, therefore η/s should scale as Nc 2 in the hadronic phase. • From Yaffe et al. η/s = A/[(g 2 Nc)2 ln(Bg 2 Nc)] with A and B known constants, therefore η/s has a finite limit as Nc becomes large in the plasma phase. • Implication: There is a jump in η/s of order Nc 2 in going from the low to the high temperature phases.
Large Nc Limit at Low T • Baryon masses are proportional to Nc and can be neglected, meson masses are essentially independent of Nc. Hagedorn temperature and critical temperature should not change by much. Meson-meson cross sections scale as 1/ Nc 2, therefore η/s should scale as Nc 2 in the hadronic phase. • From Yaffe et al. η/s = A/[(g 2 Nc)2 ln(Bg 2 Nc)] with A and B known constants, therefore η/s has a finite limit as Nc becomes large in the plasma phase. • Implication: There is a jump in η/s of order Nc 2 in going from the low to the high temperature phases.
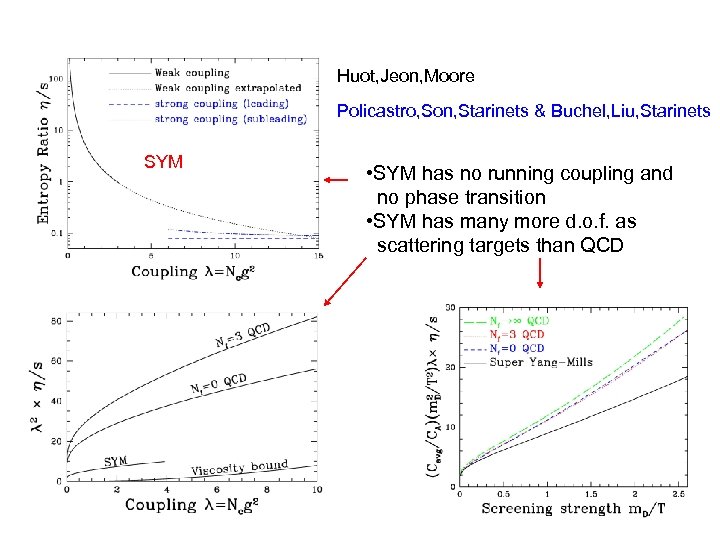 Huot, Jeon, Moore Policastro, Son, Starinets & Buchel, Liu, Starinets SYM • SYM has no running coupling and no phase transition • SYM has many more d. o. f. as scattering targets than QCD
Huot, Jeon, Moore Policastro, Son, Starinets & Buchel, Liu, Starinets SYM • SYM has no running coupling and no phase transition • SYM has many more d. o. f. as scattering targets than QCD
 Relativistic Dissipative Fluid Dynamics In the Eckart approach u is the velocity of baryon number flow.
Relativistic Dissipative Fluid Dynamics In the Eckart approach u is the velocity of baryon number flow.
 Relativistic Dissipative Fluid Dynamics In the Landau-Lifshitz approach u is the velocity of energy transport.
Relativistic Dissipative Fluid Dynamics In the Landau-Lifshitz approach u is the velocity of energy transport.
 How is this relevant for RHIC? For baryon-free matter: transverse waves sound waves Momentum diffusion constants: Bulk viscosity is generally small unless internal degrees of freedom (rotation, vibration) can easily be excited in collisions.
How is this relevant for RHIC? For baryon-free matter: transverse waves sound waves Momentum diffusion constants: Bulk viscosity is generally small unless internal degrees of freedom (rotation, vibration) can easily be excited in collisions.
 How is this relevant for RHIC? • Solve relativistic viscous fluid equations, with appropriate initial conditions and with a hadron cascade afterburner, over a range of beam energies and nuclei and extract η(T)/s(T) from comparison with data. • An analogous program was successful in obtaining information on the compressibility of nuclear matter and on the momentumdependence of the nuclear mean-field at low beam energies.
How is this relevant for RHIC? • Solve relativistic viscous fluid equations, with appropriate initial conditions and with a hadron cascade afterburner, over a range of beam energies and nuclei and extract η(T)/s(T) from comparison with data. • An analogous program was successful in obtaining information on the compressibility of nuclear matter and on the momentumdependence of the nuclear mean-field at low beam energies.
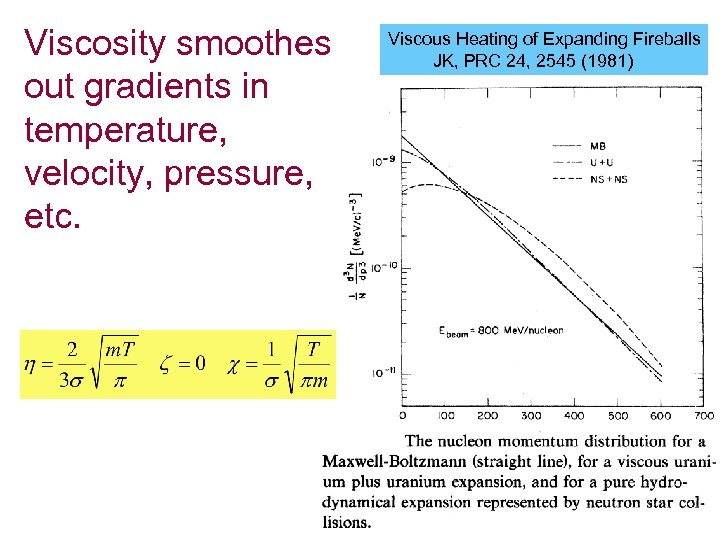 Viscosity smoothes out gradients in temperature, velocity, pressure, etc. Viscous Heating of Expanding Fireballs JK, PRC 24, 2545 (1981)
Viscosity smoothes out gradients in temperature, velocity, pressure, etc. Viscous Heating of Expanding Fireballs JK, PRC 24, 2545 (1981)
 Extracting η/s from RHIC data • • Elliptic flow (Teaney, …) HBT (Teaney, …) Momentum spectra (Teaney, Baier & Romatschke, …) Momentum fluctuations (Gavin & Abdel-Aziz, …) Fluctuations in v 2 (Csernai, …) Photon & dilepton spectra Jet quenching
Extracting η/s from RHIC data • • Elliptic flow (Teaney, …) HBT (Teaney, …) Momentum spectra (Teaney, Baier & Romatschke, …) Momentum fluctuations (Gavin & Abdel-Aziz, …) Fluctuations in v 2 (Csernai, …) Photon & dilepton spectra Jet quenching
 Work in progress…and complications • Numerical relativistic viscous fluid dynamics (Baier & Romatschke; Heinz & Song, Chaudhuri; Muronga & Rischke) Large gradients (Baier & Romatschke) may require second-order Israel-Stewart equations (Muronga). • Initial conditions (Lappi & Venugopalan CGC, …) • Hadron afterburner (Hirano, Heinz, Kharzeev, Lacey, Nora; Bass & Nonaka) • Turbulent plasmas (Asakawa, Bass, Muller) Charged particles scatter coherently from dynamically generated color fields leading to “anomalous” viscosity.
Work in progress…and complications • Numerical relativistic viscous fluid dynamics (Baier & Romatschke; Heinz & Song, Chaudhuri; Muronga & Rischke) Large gradients (Baier & Romatschke) may require second-order Israel-Stewart equations (Muronga). • Initial conditions (Lappi & Venugopalan CGC, …) • Hadron afterburner (Hirano, Heinz, Kharzeev, Lacey, Nora; Bass & Nonaka) • Turbulent plasmas (Asakawa, Bass, Muller) Charged particles scatter coherently from dynamically generated color fields leading to “anomalous” viscosity.
 Conclusion • Hadron/quark-gluon matter should have a minimum at or near the critical or crossover point in the phase diagram analogous to atomic and molecular systems. • Sufficiently detailed calculations and experiments ought to allow us to infer the viscosity/entropy ratio. This is an interesting dimensionless measure of dissipation relative to disorder.
Conclusion • Hadron/quark-gluon matter should have a minimum at or near the critical or crossover point in the phase diagram analogous to atomic and molecular systems. • Sufficiently detailed calculations and experiments ought to allow us to infer the viscosity/entropy ratio. This is an interesting dimensionless measure of dissipation relative to disorder.
 Conclusion • RHIC is a thermometer (hadron ratios, photon and lepton pair production) • RHIC is a barometer (elliptic flow, transverse flow) • RHIC may be a viscometer (deviations from ideal fluid flow) • There is plenty of work for theorists (and experimentalists)!
Conclusion • RHIC is a thermometer (hadron ratios, photon and lepton pair production) • RHIC is a barometer (elliptic flow, transverse flow) • RHIC may be a viscometer (deviations from ideal fluid flow) • There is plenty of work for theorists (and experimentalists)!


