Скачать презентацию Strong driving in Circuit QED IQC 2011 -10
24df8864357e4f727966d6fd58b41721.ppt
- Количество слайдов: 56
Strong driving in Circuit QED IQC 2011 -10 -17 Lev S Bishop Joint Quantum Institute and Condensed Matter Theory Center, University of Maryland Collaborators: Experiment: Theory: Jerry Chow (IBM) Eran Ginossar (Surrey) Andrew Houck (Princeton) Erkki Thuneberg (Oulu) Matt Reed (Yale) Jens Koch (Northwestern) Leo Di. Carlo (Delft) Steve Girvin (Yale) Dave Schuster (Chicago) Rob Schoelkopf (Yale) Funding: …
Outline • Background – Circuit QED, approximations, Jaynes-Cummings • Resonant strong coupling regime (quantum oscillator) – Photon Blockade, multiphoton transitions, supersplitting • Strong-dispersive regime (semiclassical oscillator) – Special kind of bifurcation with 2 critical points – readout • Intermediate regime – Quantum control and readout • Conclusions and future directions
Jaynes-Cummings Physics Qubit=atom=transmon Cavity=resonator coupling (two-level approx. : Rabi) (RWA: Jaynes-Cummings) Open-system (drive & dissipation) is where it gets interesting
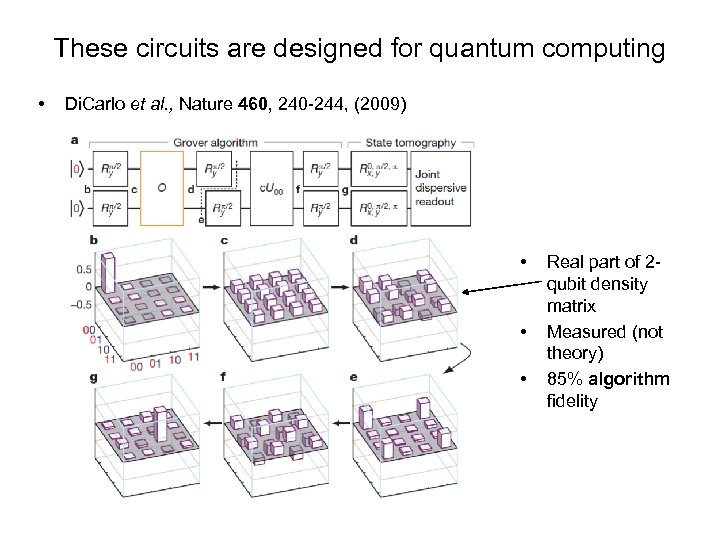These circuits are designed for quantum computing • Di. Carlo et al. , Nature 460, 240 -244, (2009) • • • Real part of 2 qubit density matrix Measured (not theory) 85% algorithm fidelity
From cavity QED to circuit QED • Strong coupling, strongly dispersive regimes: easy with circuit QED • Atom spatially fixed, no field inhomogeneity effects, etc • Drive strength easily tunable over a wide power range • Atom frequency can be tuned quickly
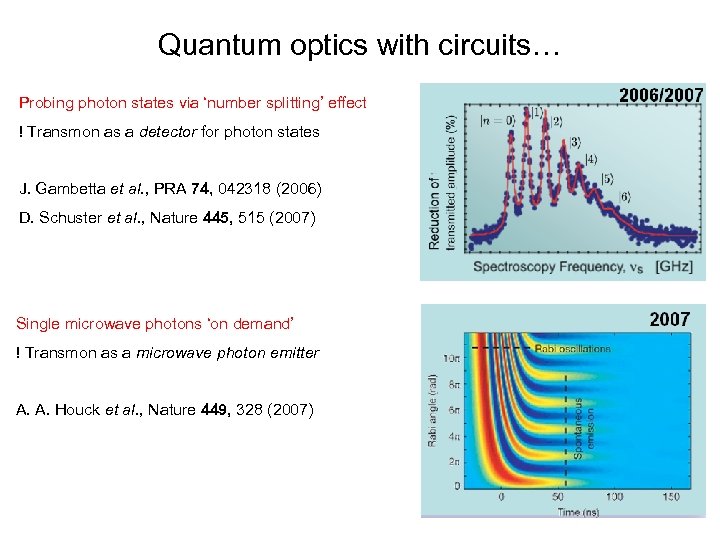Quantum optics with circuits… Probing photon states via ‘number splitting’ effect ! Transmon as a detector for photon states J. Gambetta et al. , PRA 74, 042318 (2006) D. Schuster et al. , Nature 445, 515 (2007) Single microwave photons ‘on demand’ ! Transmon as a microwave photon emitter A. A. Houck et al. , Nature 449, 328 (2007)
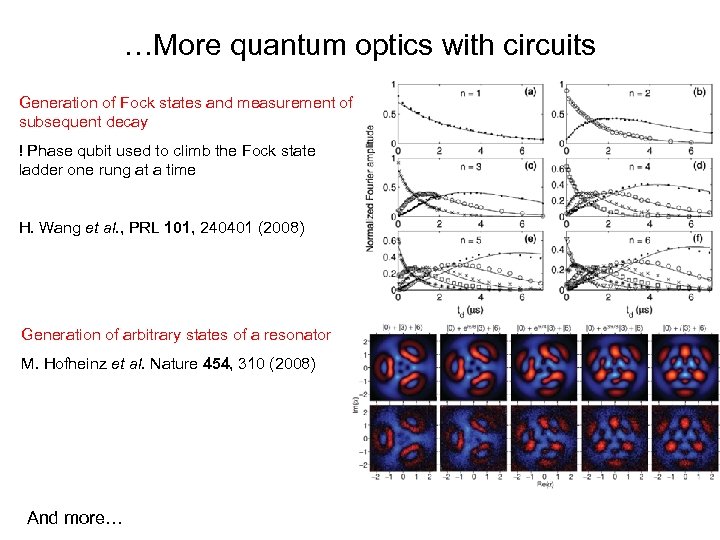…More quantum optics with circuits Generation of Fock states and measurement of subsequent decay ! Phase qubit used to climb the Fock state ladder one rung at a time H. Wang et al. , PRL 101, 240401 (2008) Generation of arbitrary states of a resonator M. Hofheinz et al. Nature 454, 310 (2008) And more…
Outline • Background – Circuit QED, approximations, Jaynes-Cummings • Resonant strong coupling regime (quantum oscillator) – Photon Blockade, multiphoton transitions, supersplitting • Strong-dispersive regime (semiclassical oscillator) – Special kind of bifurcation with 2 critical points – readout • Intermediate regime – Quantum control and readout • Conclusions and future directions
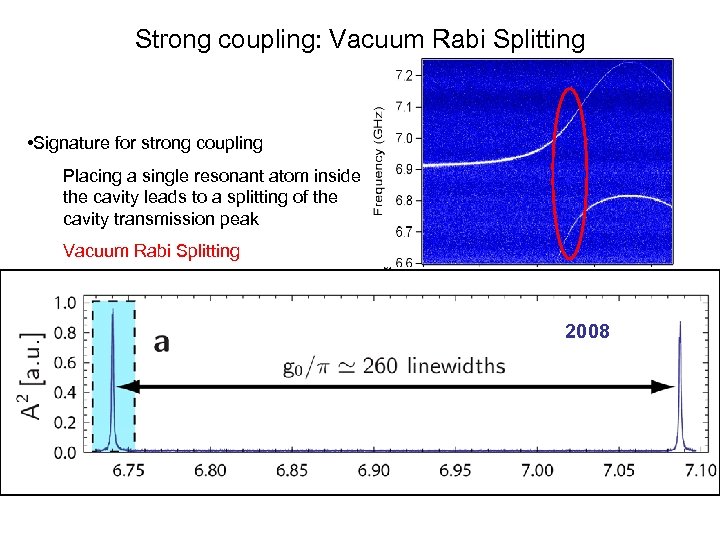Strong coupling: Vacuum Rabi Splitting • Signature for strong coupling Placing a single resonant atom inside the cavity leads to a splitting of the cavity transmission peak Vacuum Rabi Splitting Observed in: Cavity QED: R. J. Thompson et al, Phys. Rev. Lett 68, 1132 (1992) 2008 Circuit QED: A. Wallraff et al. , Nature 431, 162 (2004) Quantum dot systems: J. P. Reithmaier et al. , Nature 432, 197 (2004) T. Yoshie et al. , Nature 432, 200 (2004) A. Wallraff et al. , Nature 431, 162 (2004)
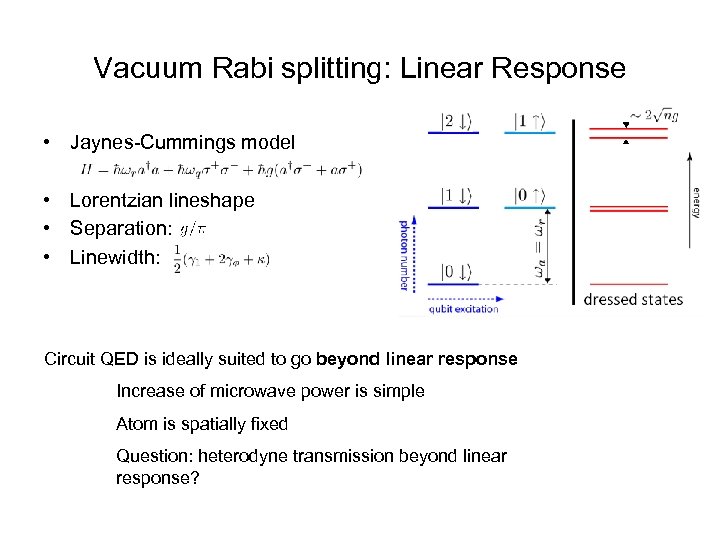Vacuum Rabi splitting: Linear Response • Jaynes-Cummings model • Lorentzian lineshape • Separation: • Linewidth: Circuit QED is ideally suited to go beyond linear response Increase of microwave power is simple Atom is spatially fixed Question: heterodyne transmission beyond linear response?
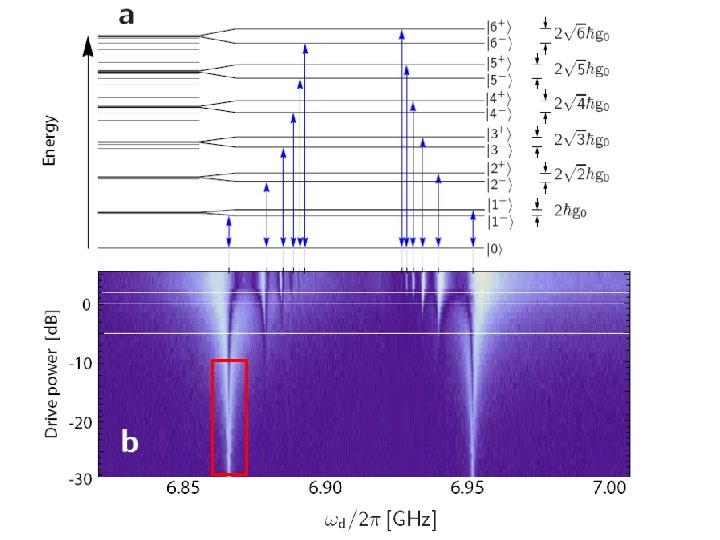
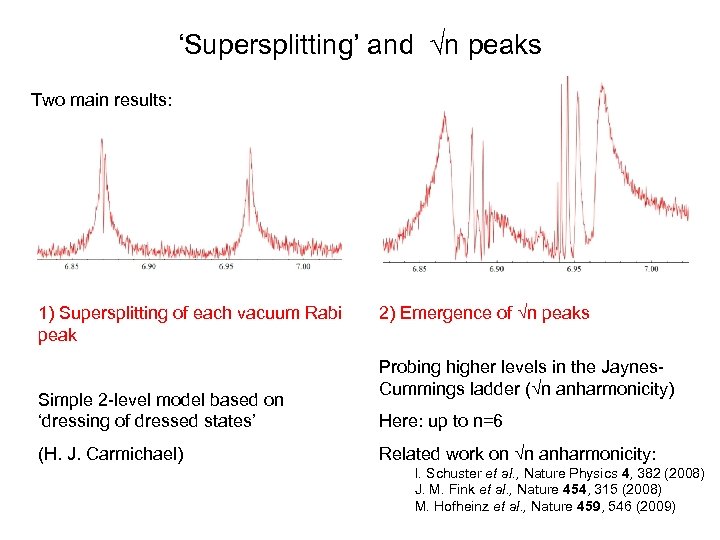‘Supersplitting’ and n peaks Two main results: 1) Supersplitting of each vacuum Rabi peak Simple 2 -level model based on ‘dressing of dressed states’ (H. J. Carmichael) 2) Emergence of n peaks Probing higher levels in the Jaynes. Cummings ladder ( n anharmonicity) Here: up to n=6 Related work on n anharmonicity: I. Schuster et al. , Nature Physics 4, 382 (2008) J. M. Fink et al. , Nature 454, 315 (2008) M. Hofheinz et al. , Nature 459, 546 (2009)
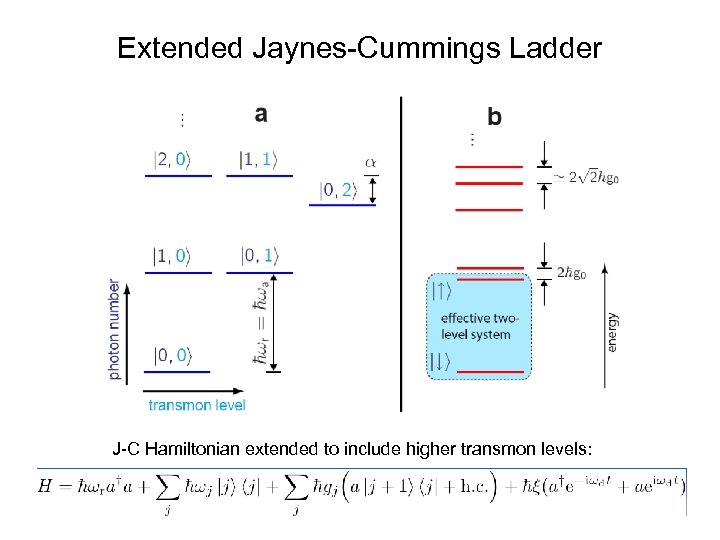Extended Jaynes-Cummings Ladder J-C Hamiltonian extended to include higher transmon levels:
Supersplitting: 2 -level model Restriction to 2 -level subspace: ‘Dressing of dressed states’ Measure heterodyne amplitude: (Not aya as in photon counting) Steady state solution of Bloch equations: (T 1, T 2 get renormalized)
Full model • Extended Jaynes-Cummings Hamiltonian with drive: • Include dissipation via Master equation • Measure heterodyne transmission amplitude, not
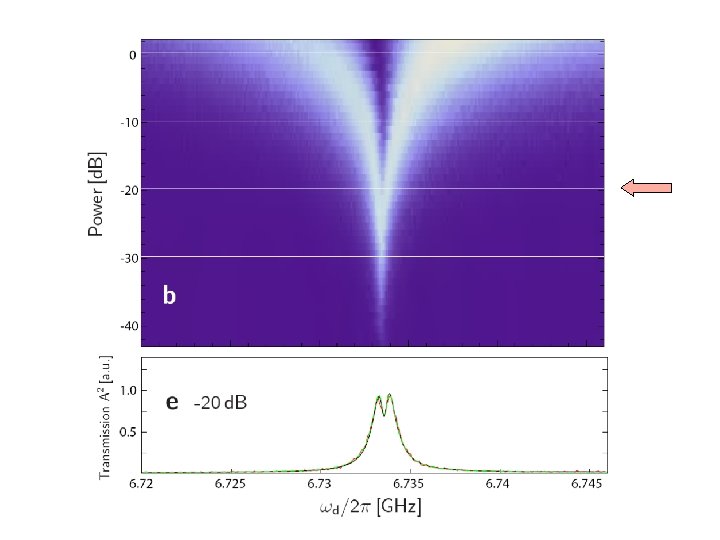
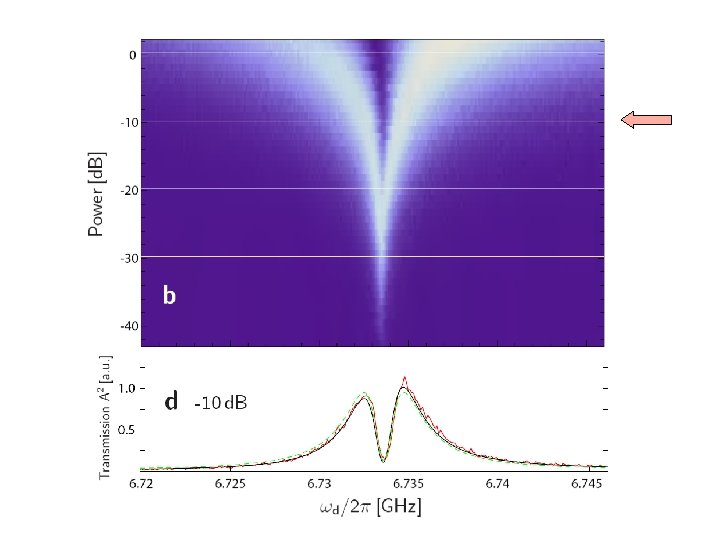
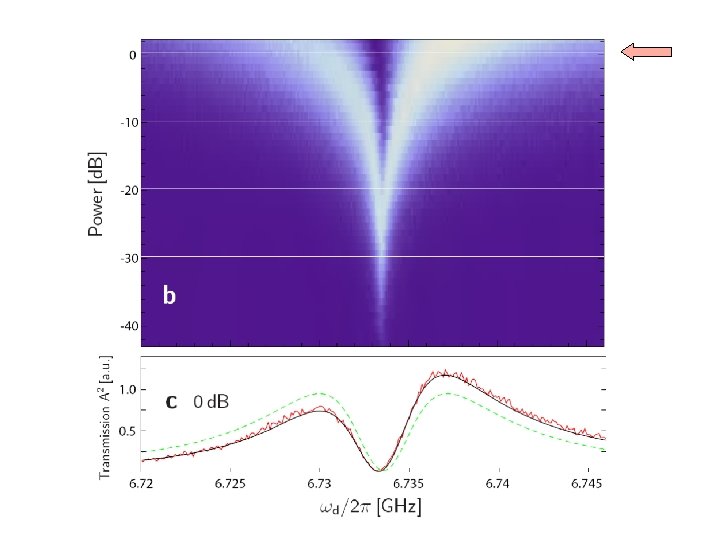
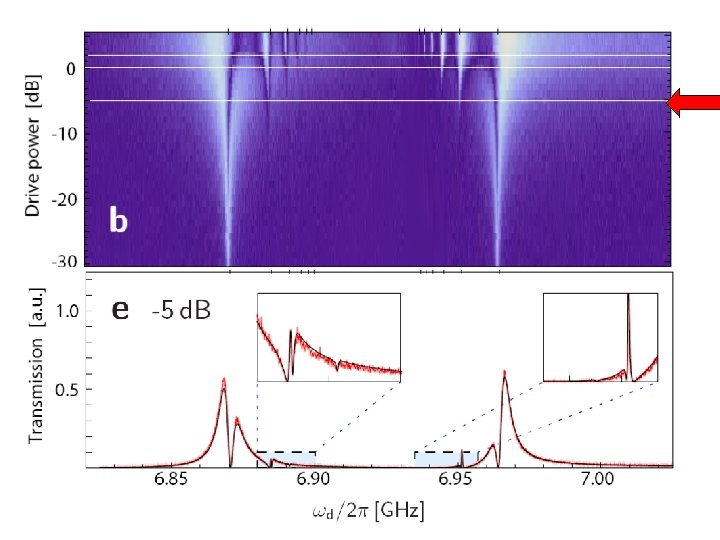
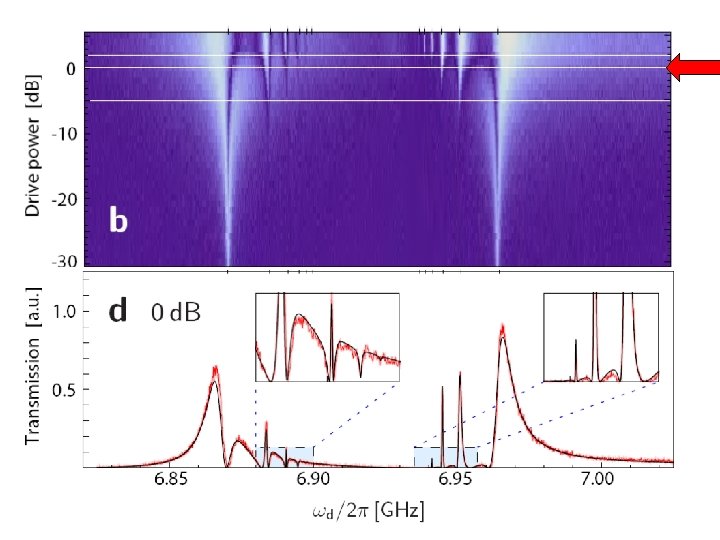
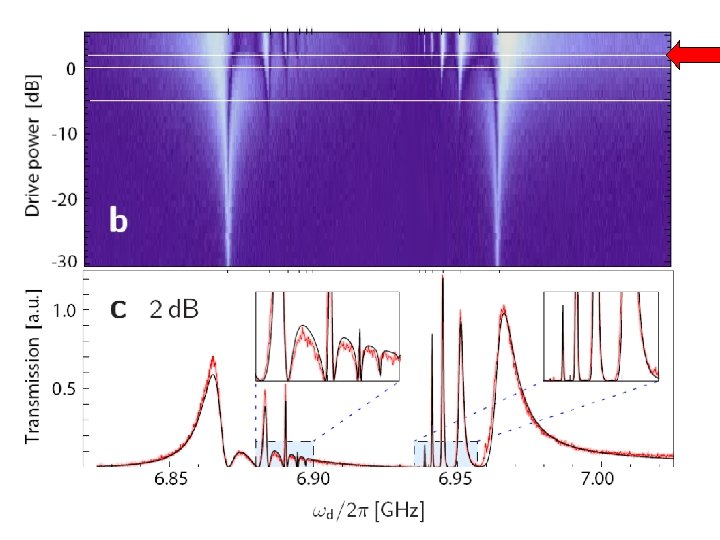
Outline • Background – Circuit QED, approximations, Jaynes-Cummings • Resonant strong coupling regime (quantum oscillator) – Photon Blockade, multiphoton transitions, supersplitting • Strong-dispersive regime (semiclassical oscillator) – Special kind of bifurcation with 2 critical points – readout • Intermediate regime – Quantum control and readout • Conclusions and future directions LSB, Ginossar, Girvin PRL 105, 100505 (2010) Boissonneault, Gambetta, Blais PRL 105, 100504 (2010) Reed et al PRL 105, 173601 (2010)
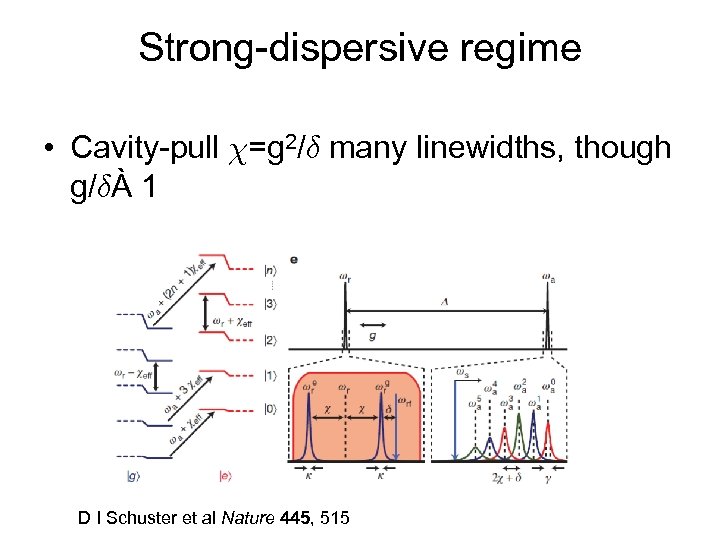Strong-dispersive regime • Cavity-pull =g 2/± many linewidths, though g/±À 1 D I Schuster et al Nature 445, 515
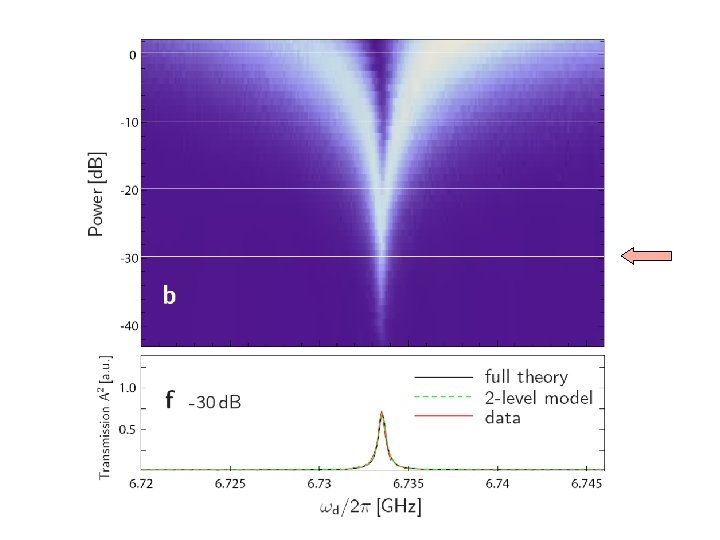
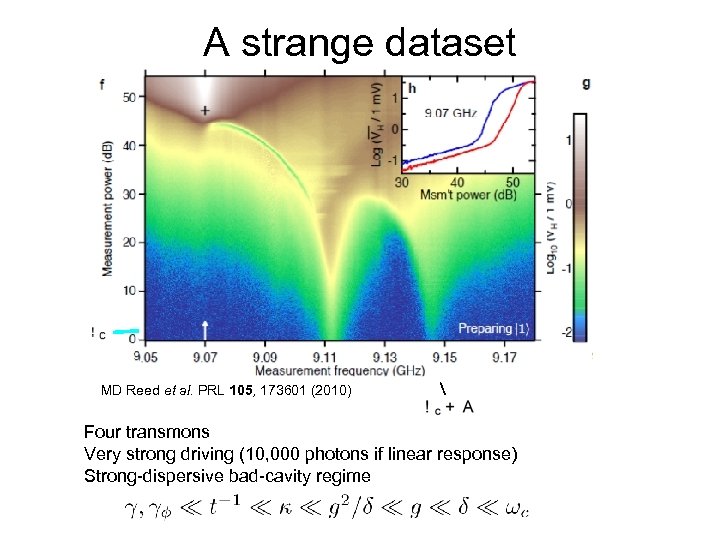A strange dataset MD Reed et al. PRL 105, 173601 (2010) Four transmons Very strong driving (10, 000 photons if linear response) Strong-dispersive bad-cavity regime
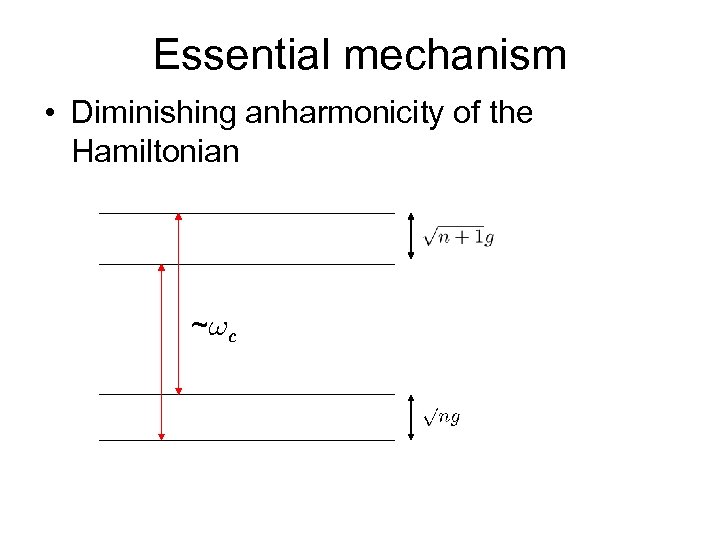Essential mechanism • Diminishing anharmonicity of the Hamiltonian ~!c
Undriven Hamiltonian JC Hamiltonian HUGE simplification: seems unlikely to be useful but let’s try anyway Exact Diagonalization detuning total excitations critical photon number
Perturbative expansion Expand in Dispersive approximation Plus Kerr term… Can continue the expansion, but only converges for For typical c. QED parameters, the dispersive approximation breaks down 3 before N=Ncrit: anharmonicity ®=2 g 4/± is approx. linewidth g=200 MHz, ±=1 GHz, ®=3. 2 MHz
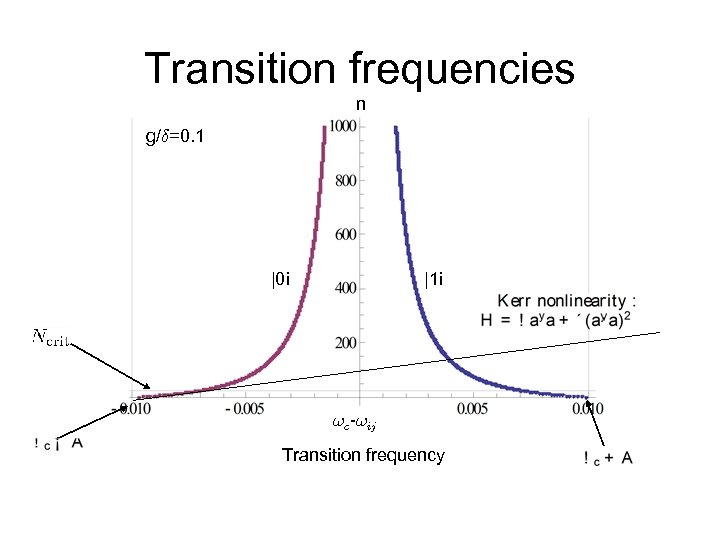Transition frequencies n g/±=0. 1 |0 i |1 i !c-!ij Transition frequency
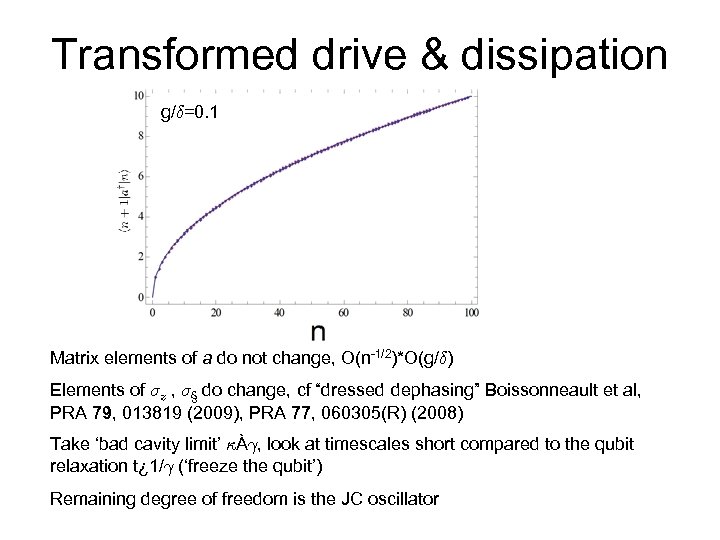Transformed drive & dissipation g/±=0. 1 Matrix elements of a do not change, O(n-1/2)*O(g/±) Elements of ¾z , ¾§ do change, cf “dressed dephasing” Boissonneault et al, PRA 79, 013819 (2009), PRA 77, 060305(R) (2008) Take ‘bad cavity limit’ ·À°, look at timescales short compared to the qubit relaxation t¿ 1/° (‘freeze the qubit’) Remaining degree of freedom is the JC oscillator
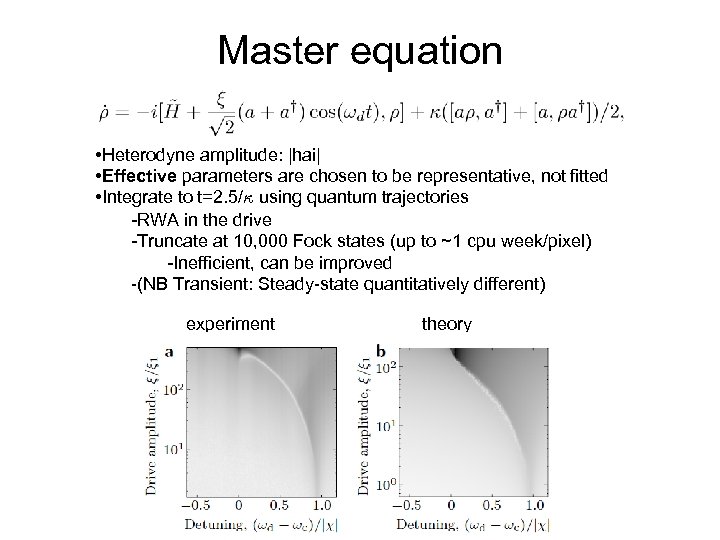Master equation • Heterodyne amplitude: |hai| • Effective parameters are chosen to be representative, not fitted • Integrate to t=2. 5/· using quantum trajectories -RWA in the drive -Truncate at 10, 000 Fock states (up to ~1 cpu week/pixel) -Inefficient, can be improved -(NB Transient: Steady-state quantitatively different) experiment theory
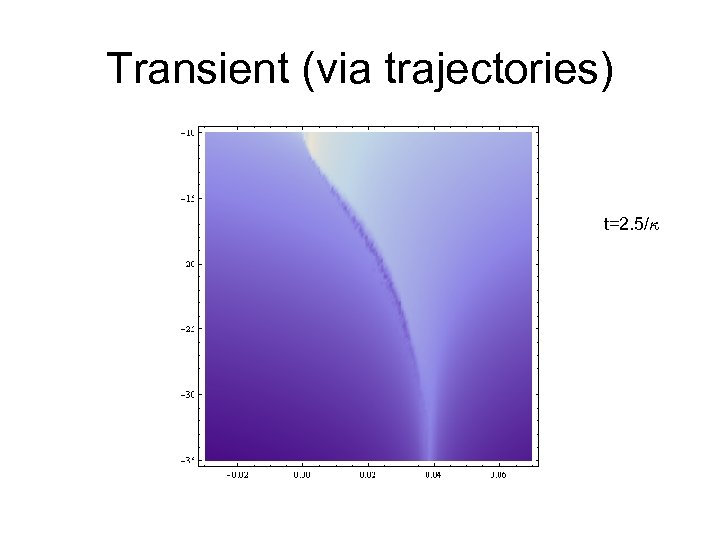Transient (via trajectories) t=2. 5/·
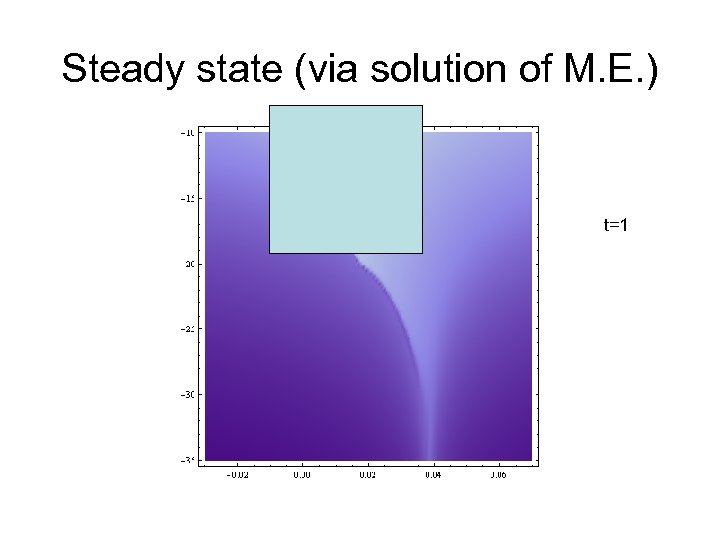Steady state (via solution of M. E. ) t=1
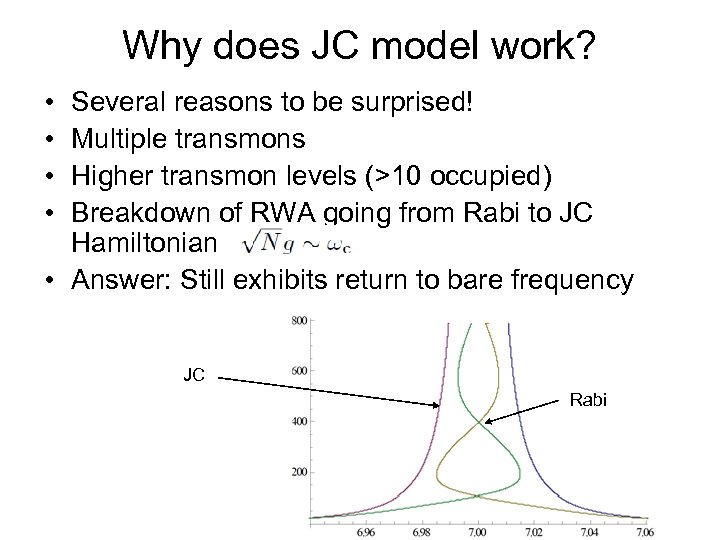Why does JC model work? • • Several reasons to be surprised! Multiple transmons Higher transmon levels (>10 occupied) Breakdown of RWA going from Rabi to JC Hamiltonian • Answer: Still exhibits return to bare frequency JC Rabi
Semiclassical JC Oscillator • Quantum model works nicely, but want to simplify further • In limit of anharmonicity ¿ linewidth. – final part of my talk is about opposite limit • Rewrite Hamiltonian in terms of canonical variables gives cf Peano & Thorwart, EPL 89, 17008 (2010)
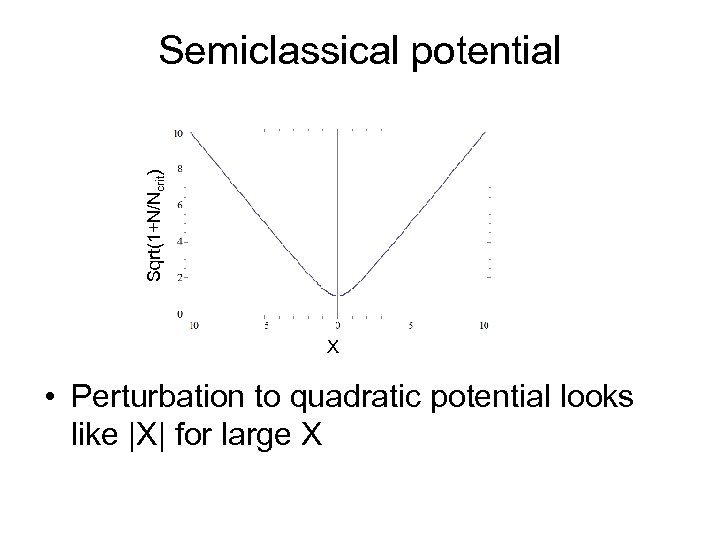Sqrt(1+N/Ncrit) Semiclassical potential X • Perturbation to quadratic potential looks like |X| for large X
Semiclassical equation • Self-consistent equations for the amplitude A 2=X 2+P 2 • Treat A as constant (ignore harmonic generation, chaos)
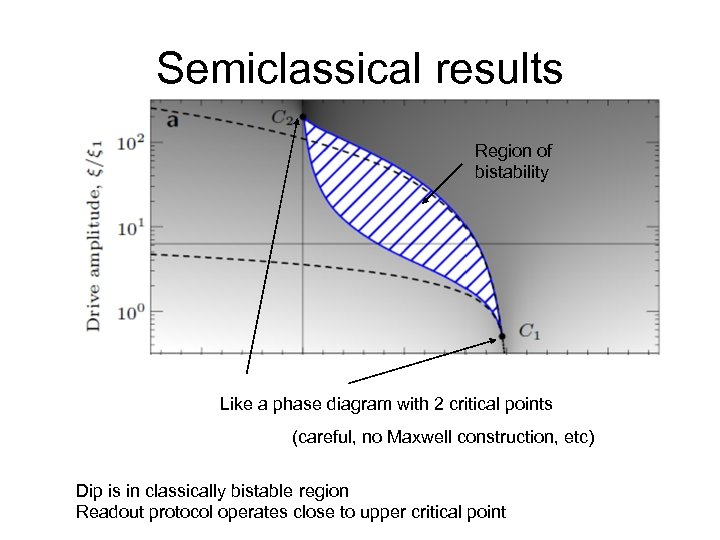Semiclassical results Region of bistability Like a phase diagram with 2 critical points (careful, no Maxwell construction, etc) Dip is in classically bistable region Readout protocol operates close to upper critical point
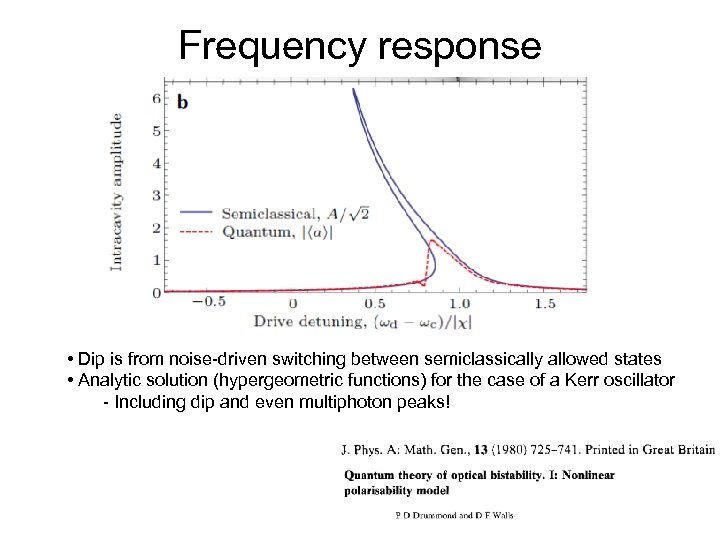Frequency response • Dip is from noise-driven switching between semiclassically allowed states • Analytic solution (hypergeometric functions) for the case of a Kerr oscillator - Including dip and even multiphoton peaks!
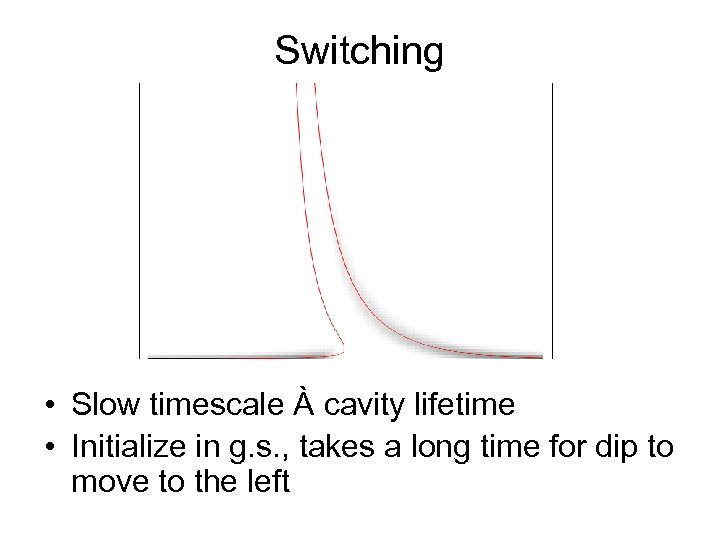Switching • Slow timescale À cavity lifetime • Initialize in g. s. , takes a long time for dip to move to the left
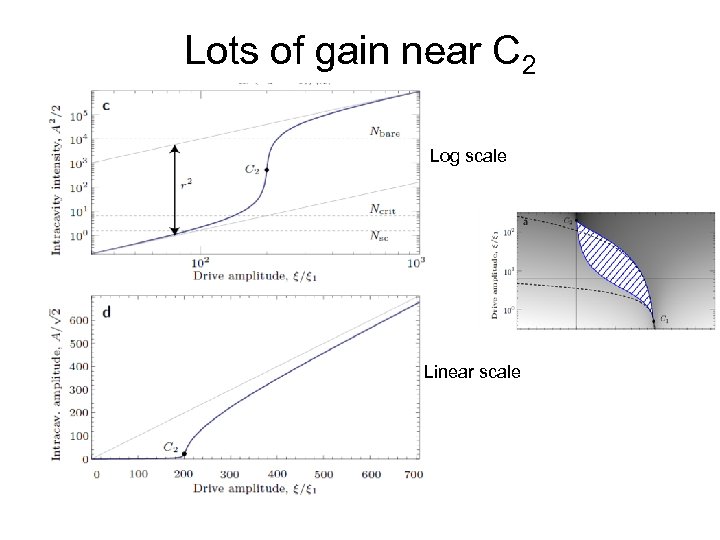Lots of gain near C 2 Log scale Linear scale
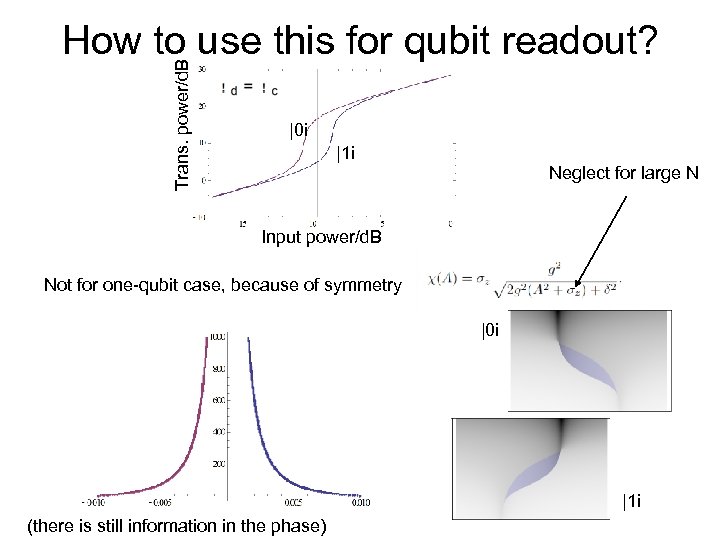Trans. power/d. B How to use this for qubit readout? |0 i |1 i Neglect for large N Input power/d. B Not for one-qubit case, because of symmetry |0 i |1 i (there is still information in the phase)
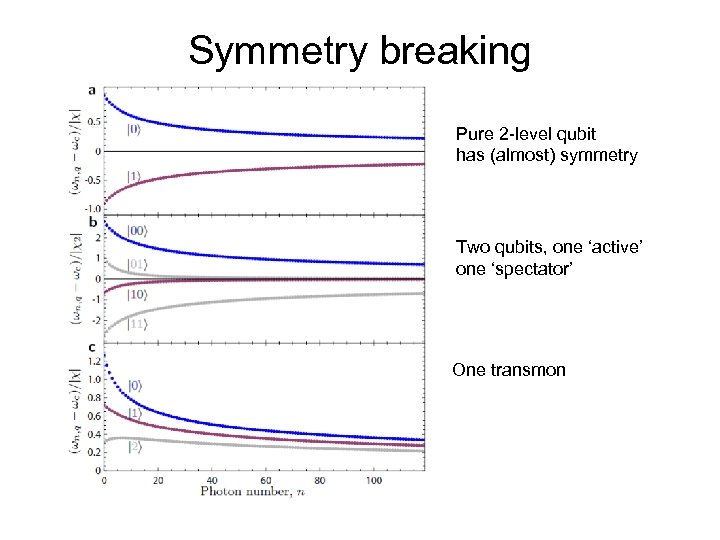Symmetry breaking Pure 2 -level qubit has (almost) symmetry Two qubits, one ‘active’ one ‘spectator’ One transmon
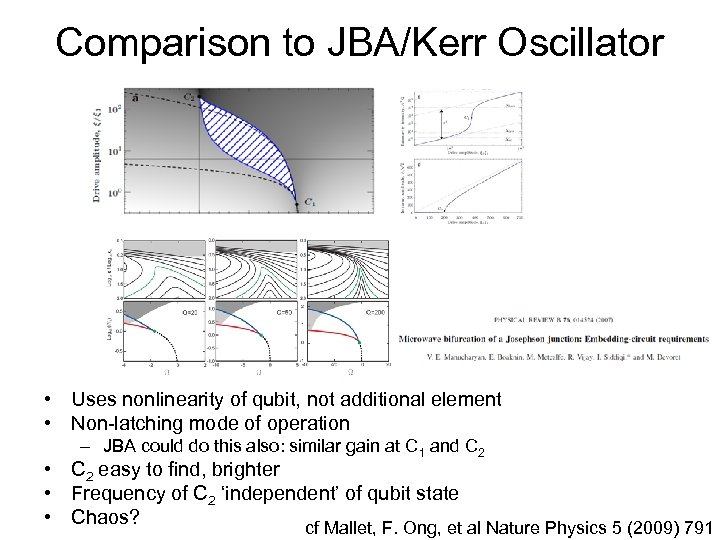Comparison to JBA/Kerr Oscillator • Uses nonlinearity of qubit, not additional element • Non-latching mode of operation – JBA could do this also: similar gain at C 1 and C 2 • C 2 easy to find, brighter • Frequency of C 2 ‘independent’ of qubit state • Chaos? cf Mallet, F. Ong, et al Nature Physics 5 (2009) 791
Other single-atom bistabilities • Absorptive bistability – V. different regime: weak coupling, good cavity – Maxwell-Bloch (keeps qubit dynamics) • Spontaneous dressed-state polarization/single-atom phase stability – Strong coupling, bad cavity – But: qubit & cavity on resonance – Drive above ‘» 2’
Conclusions • JC oscillator is appropriate qualitative model for the readout – Surprising: return to bare frequency is the important thing • • • Beyond dispersive approximation Beyond Kerr nonlinearity Beyond perturbation expansion A new kind of nonlinear oscillator(? ) Lots of gain at C 2 Special kind of symmetry breaking (» 2 depends on transmon state(s), but not 2) – Is very helpful for readout
Outline • Background – Circuit QED, approximations, Jaynes-Cummings • Resonant strong coupling regime (quantum oscillator) – Photon Blockade, multiphoton transitions, supersplitting • Strong-dispersive regime (semiclassical oscillator) – Special kind of bifurcation with 2 critical points – readout • Intermediate regime – Quantum control and readout • Conclusions and future directions Ginossar, LSB, Schuster, Girvin. Phys. Rev. A 82, 022335 (2010)
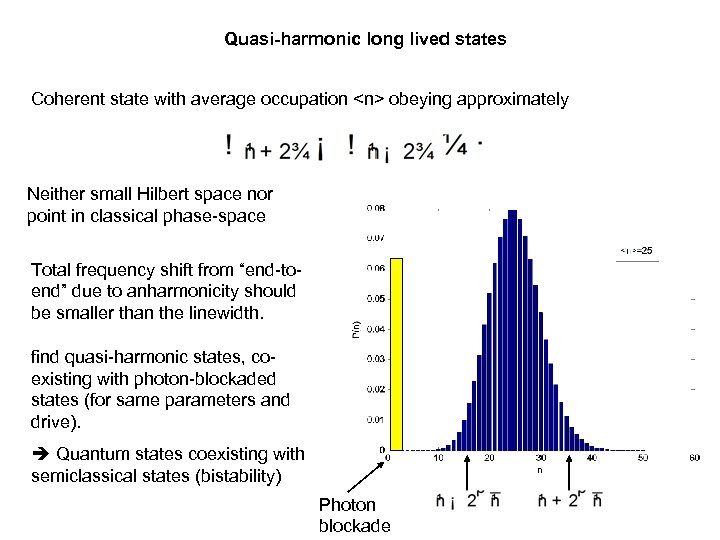Quasi-harmonic long lived states Coherent state with average occupation
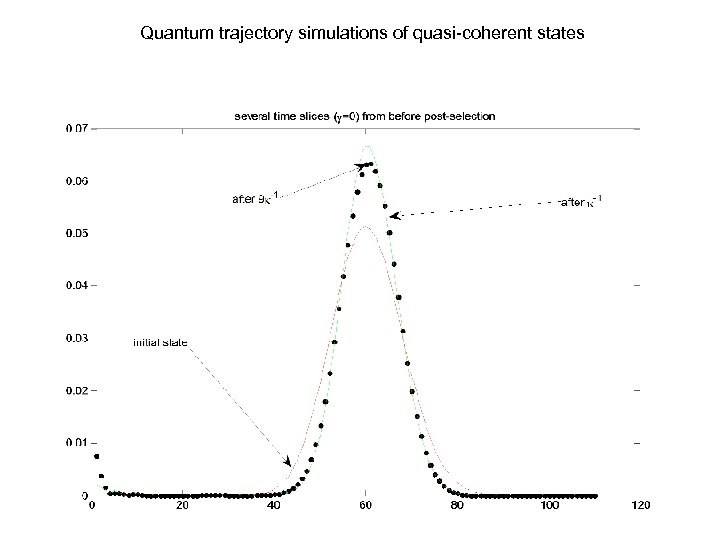Quantum trajectory simulations of quasi-coherent states
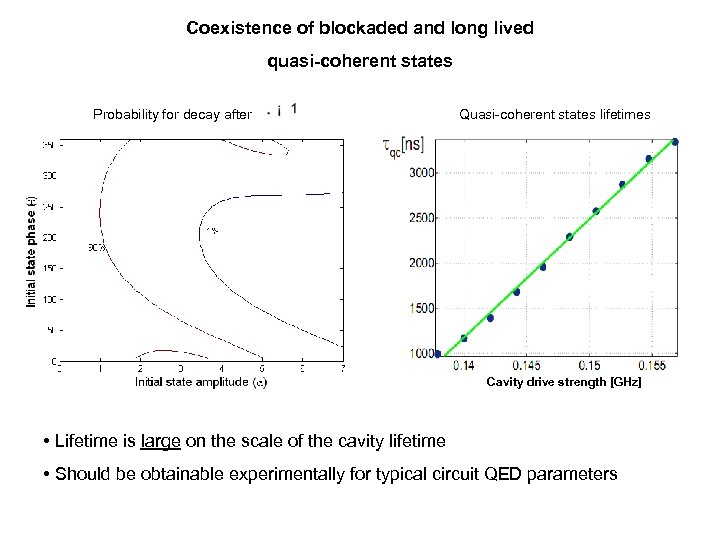Coexistence of blockaded and long lived quasi-coherent states Probability for decay after Quasi-coherent states lifetimes Cavity drive strength [GHz] • Lifetime is large on the scale of the cavity lifetime • Should be obtainable experimentally for typical circuit QED parameters
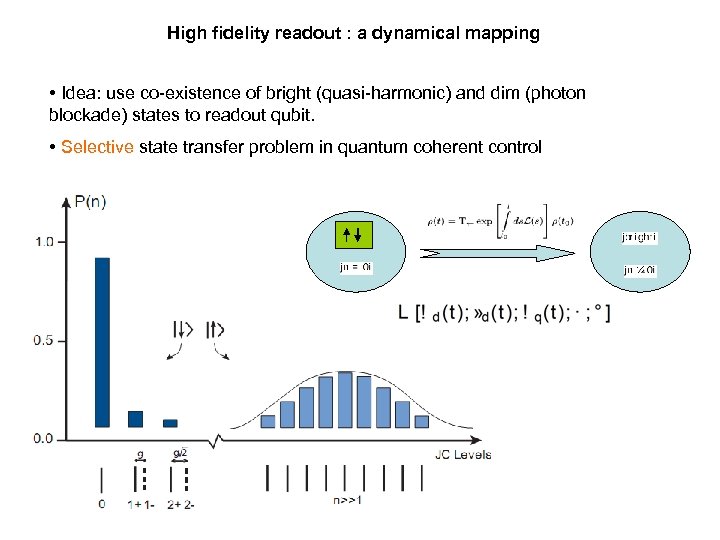High fidelity readout : a dynamical mapping • Idea: use co-existence of bright (quasi-harmonic) and dim (photon blockade) states to readout qubit. • Selective state transfer problem in quantum coherent control
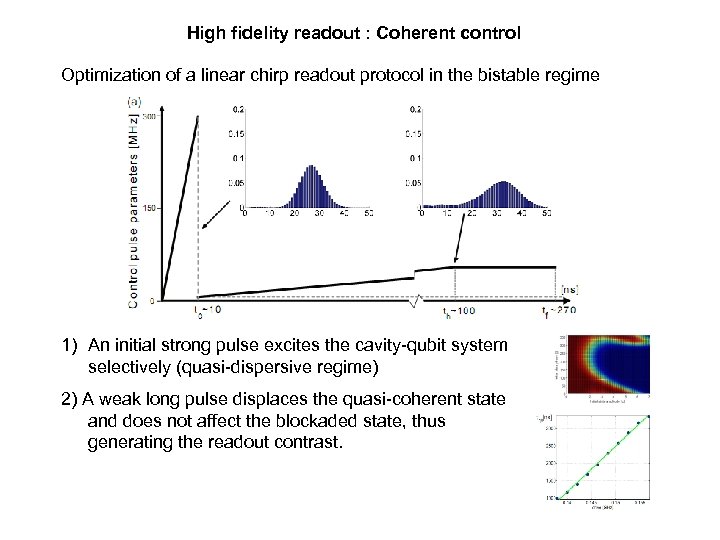High fidelity readout : Coherent control Optimization of a linear chirp readout protocol in the bistable regime 1) An initial strong pulse excites the cavity-qubit system selectively (quasi-dispersive regime) 2) A weak long pulse displaces the quasi-coherent state and does not affect the blockaded state, thus generating the readout contrast.
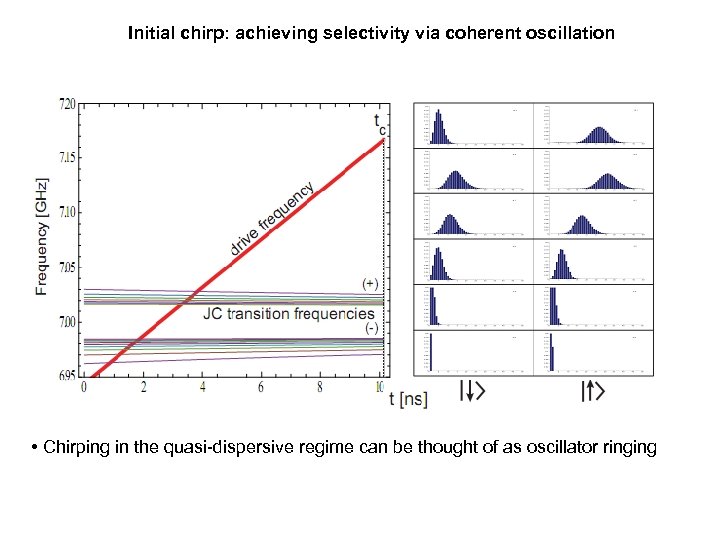Initial chirp: achieving selectivity via coherent oscillation • Chirping in the quasi-dispersive regime can be thought of as oscillator ringing
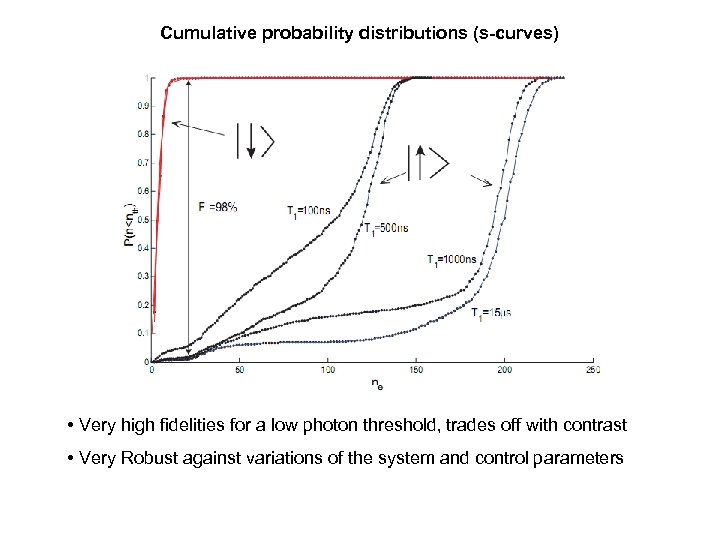Cumulative probability distributions (s-curves) • Very high fidelities for a low photon threshold, trades off with contrast • Very Robust against variations of the system and control parameters
Summary and outlook • New type of bistability in the JC ladder between photon blockaded states and quasi-coherent metastable states. • See also Di. Vincenzo and Smolin ar. Xiv: 1109. 2490 (2011). • We demonstrated an efficient coherent control protocol for high fidelity (98%) readout, with full quantum mechanical simulation including the decay processes. • A simple architecture: apply a different readout protocol -No additional parts necessary on the circuit except the qubit and cavity. Open questions: • Theory for the timescales for switching between the bistable states? • Apply optimal control • Consider multi-qubit readout? • Effect of additional levels of realistic (e. g. Transmon) systems.
Overall conclusions • Extreme parameters of circuit QED (compared to other cavity QED implementations) allow observation of interesting quantum optics effects in different regimes • These can be useful for qubit readout • Some other strong driving effects (many others): – Autler-Townes, Mollow triplet (Baur et al Phys. Rev. Lett. 102, 243602 (2009)), (Li et al Phys. Rev. B 84, 104527 (2011)) – Photon blockade (Hoffman et al Phys. Rev. Lett. 107, 053602 (2011)) • Quantum control – For gates, eg DRAG and GRAPE (Motzoi et al Phys. Rev. Lett. 103, 110501 (2009)) – For readout, eg chirped driving/autoresonance (Naaman et al PRL 101, 117005 (2008) • Better qubits, fancier architectures (multiple cavities), additional nonlinear elements, etc • Some inspiration from other cavity QED implementations, some unique to circuits. See forthcoming “Fluctuating nonlinear oscillators” M. Dykman (ed), OUP (2011). Thank you!