СТРОИТЕЛЬНАЯ МЕХАНИКА Лекция 1 Кинематический Кинематически структурный

СТРОИТЕЛЬНАЯ МЕХАНИКА Лекция № 1. Кинематический Кинематически структурный анализ расчетн схем

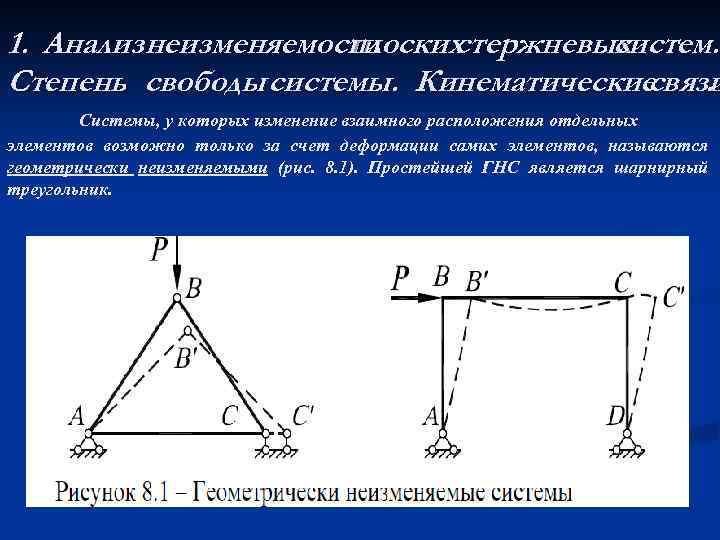1. Анализ неизменяемости плоских стержневых систем. Степень свободы системы. Кинематические. связи Системы, у которых изменение взаимного расположения отдельных элементов возможно только за счет деформации самих элементов, называются геометрически неизменяемыми (рис. 8. 1). Простейшей ГНС является шарнирный треугольник.

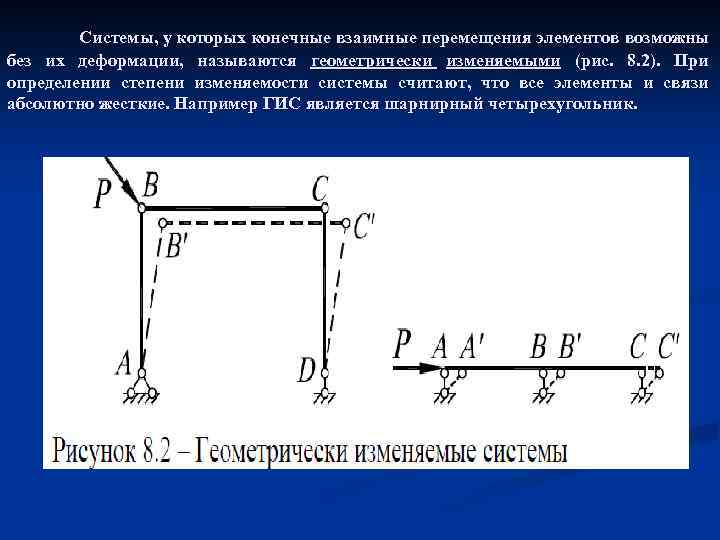Системы, у которых конечные взаимные перемещения элементов возможны без их деформации, называются геометрически изменяемыми (рис. 8. 2). При определении степени изменяемости системы считают, что все элементы и связи абсолютно жесткие. Например ГИС является шарнирный четырехугольник.

Элементами системы могут быть отдельные стержни, пластинки и массивы. Эти элементы и их группы можно считать абсолютно жёсткими телами. В плоских системах такие тела называют жёсткими дисками (диск принято изображать плоской фигурой произвольного очертания). Диски соединяются между собой шарнирами и стержнями и прикрепляются к земле (основанию) с помощью опорных стержней (связей). В число дисков может входить основание (неподвижное тело, на которое опирается система). Стержень, оба конца которого шарнирно соединены с дисками, называют соединительным. Соединительный стержень препятствует поступательному перемещению одного диска относительно другого по направлению связующего стержня. При действии внешних сил на диски в связи возникает реакция, направленная вдоль оси стержня.

Шарнир, соединяющий между собой два диска, называют простым шарниром. Шарнир эквивалентен двум связям. Если шарнир соединяет n дисков (n > 2) , его называют кратным. Кратный шарнир (рис. 8. 3 -а, б) эквивалентен (n − 1) простым шарнирам. n n Жесткая связь (сварка, пайка), соединяющая два диска, препятствует поступательным движениям по горизонтальному, вертикальному направлениям и повороту их относительно друга. Простая жесткая связь эквивалентна трем стержням.

Анализ сооружения начинается с определения степени свободы системы. Степенью свободы системы называется кинематическая характеристика, определяющая наименьшее число независимых параметров, с помощью которых можно определить положение всех точек системы в любой момент времени. Каждый жесткий диск в плоскости имеет три степени свободы, то есть его положение в плоскости определяется тремя независимыми координатами: двумя поступательными перемещениями по направлению координатных осей x и y и поворотом в плоскости xy (рис. 8. 4). Ограничить число возможных перемещений системы можно путем наложения на нее связей.

Кинематический метод проверки геометрической неизменяемости по формуле Чебышева n Пусть схема содержит D – жестких дисков, Ш – простых шарниров, С 0 – опорных стержней. Тогда легко подсчитать число степеней свободы – W рассматриваемой системы: W = 3 D − 2 Ш −С 0. (8. 1) n n n При кинематическом анализе расчетной схемы сооружения могут встретиться три случая: W > 0 – система является геометрически изменяемой и по определению не может служить в качестве расчётной схемы сооружения; W < 0 – система имеет избыточное число связей. В этом случае можно утверждать, что при правильной расстановке связей система является статически неопределимой, но ничего определенного сказать нельзя относительно кинематической неизменяемости системы; W = 0 – система формально содержит достаточное количество связей, чтобы считать ее геометрически неизменяемой и статически определимой. Таким образом, необходимым условием геометрической неизменяемости системы является условие 3 D − 2 Ш −С 0 ≤ 0. (8. 2) n При кинематическом анализе свободных систем, то есть не связанных с землей или основанием, из условия геометрической неизменяемости удаляется слагаемое, учитывающие число опорных связей (C 0 = 0), а степень свободы всей системы уменьшается на три. С учетом выше изложенного степень свободы свободных систем определяется по формуле W = 3 D − 2 Ш − 3, (8. 3) n а условие геометрической неизменяемости имеет вид 3 D − 2 Ш − 3 ≤ 0. (8. 4)

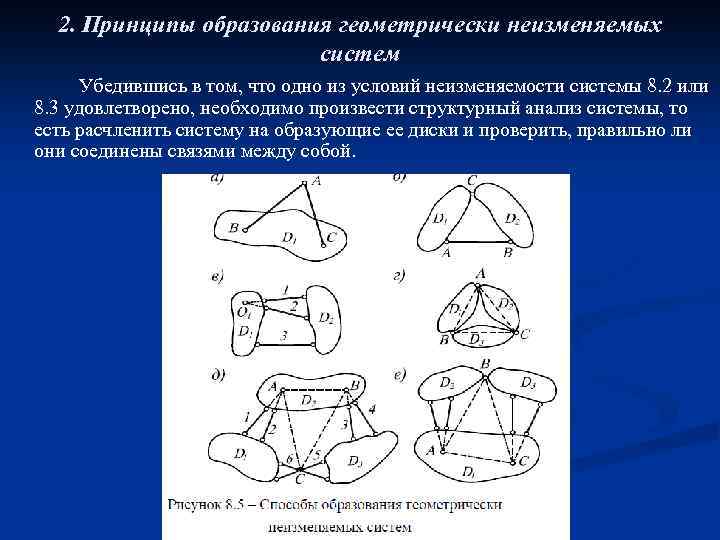2. Принципы образования геометрически неизменяемых систем Убедившись в том, что одно из условий неизменяемости системы 8. 2 или 8. 3 удовлетворено, необходимо произвести структурный анализ системы, то есть расчленить систему на образующие ее диски и проверить, правильно ли они соединены связями между собой.

3. Мгновенно изменяемые системы Мгновенно изменяемая система это система, которая допускает без деформации составляющих ее элементов бесконечно малые перемещения этих элементов лишь на мгновение, после чего она снова становится неизменяемой. В мгновенно изменяемых системах могут возникнуть большие усилия и перемещения, недопустимые при эксплуатации.

Исследуем на мгновенную изменяемость систему

Исследуем на мгновенную изменяемость систему

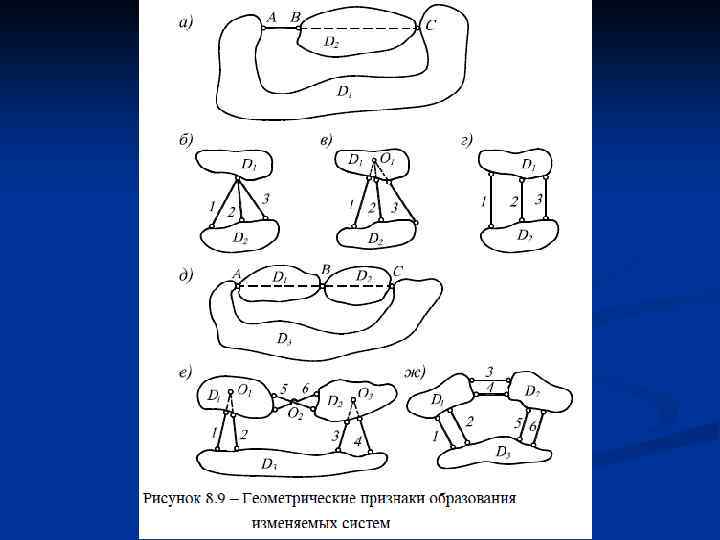
Статические признаки мгновенно изменяемых систем: − возникновение в отдельных элементах системы, которая имеет достаточное количество связей, бесконечно больших сил; − возникновение в отдельных элементах системы, которая имеет достаточное количество связей, неопределенных сил. Геометрические признаки мгновенно изменяемых систем: − два диска D 1 и D 2 соединены шарниром С и стержнем AB лежащими на одной прямой (рис. 8. 9 -а); − два диска D 1 и D 2 соединены стержнями 1, 2 и 3, оси которых и их продолжения пересекаются в одной точке, или параллельны (рис. 8. 9 -б, в, г); − три диска D 1 , D 2 и D 3 соединены шарнирами A , B и C лежащими на одной прямой (рис. 8. 9 -д); − три диска D 1 , D 2 и D 3 соединены шестью связями точки пересечения каждой из пар 1 и 2, 3 и 4, 5 и 6 лежат на одной прямой или параллельны (рис. 8. 9 -е, ж).

5. Кинематический анализ ферм Ферма, как и всякое сооружение, должна быть неподвижной относительно земли и геометрически неизменяемой. Геометрическая неизменяемость фермы достигается правильным соединением стержней или отдельных дисков, входящих в состав ферм. Для подсчета числа степеней свободы ферм можно элементами считать ее узлы, а стержни, соединяющие узлы – связями. При этом каждый узел считается обладающим двумя степенями свободы в плоскости. Условие геометрической неизменяемости ферм: где У – число узлов фермы; С – число стержней фермы; С 0 – число опорных стержней фермы.

Условие геометрической неизменяемости для ферм является необходимым, но не достаточным. Его следует дополнить проверкой правильности структуры фермы, которая следует из способов образования плоских ферм. При анализе геометрической структуры ферм следует учитывать, что простейшей геометрически неизменяемой шарнирной системой является шарнирный треугольник. Присоединяя к нему узлы с помощью двух стержней, оси которых не лежат на одной прямой – диады можно образовать новую более сложную геометрически неизменяемую систему (рис. 1. 11).

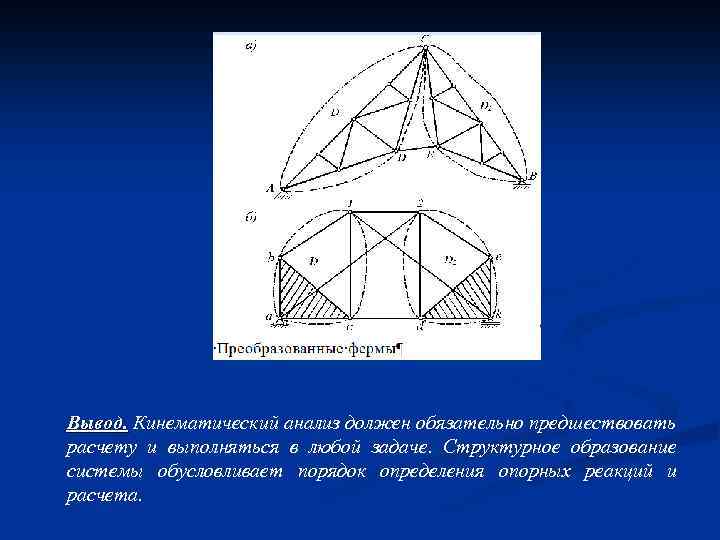Вывод. Кинематический анализ должен обязательно предшествовать расчету и выполняться в любой задаче. Структурное образование системы обусловливает порядок определения опорных реакций и расчета.