Streamline Verification Process with Formal Property Verification to

Streamline Verification Process with Formal Property Verification to Meet Highly Compressed Design Cycle Prosenjit Chatterjee, n. VIDIA Corporation

Goals n Reach conventional verification goals faster n Reach more verification goals n Fewer verification resources n Prove specific properties of most complex blocks

SFV n Minimal verification environment expertise n Ability to use conventional verification techniques n Non FV-able properties still usable n Use conventional verification techniques at Full Chip and Super Unit level n However, now fewer bugs to uncover as sub-units are already SFV-ed n Full time Dedicated Verification Engineer not required n Designer’s kit

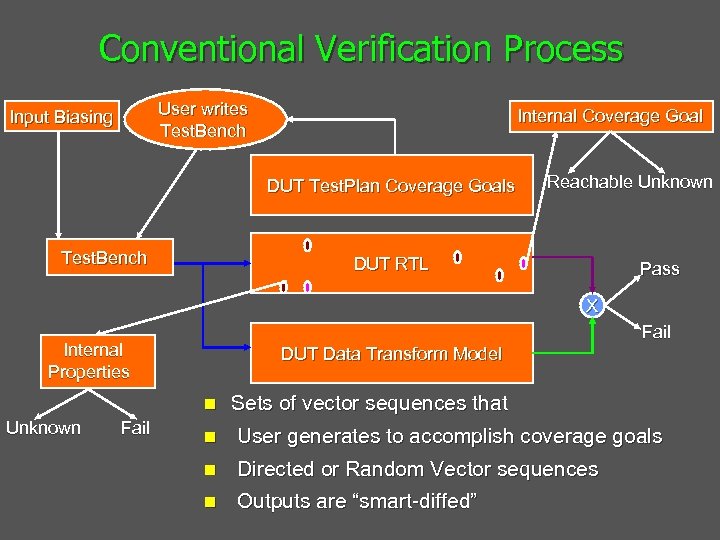Conventional Verification Process User writes Test. Bench Input Biasing Internal Coverage Goal DUT Test. Plan Coverage Goals Test. Bench Reachable Unknown DUT RTL Pass X Fail Internal Properties DUT Data Transform Model n Unknown Fail Sets of vector sequences that n User generates to accomplish coverage goals n Directed or Random Vector sequences n Outputs are “smart-diffed”

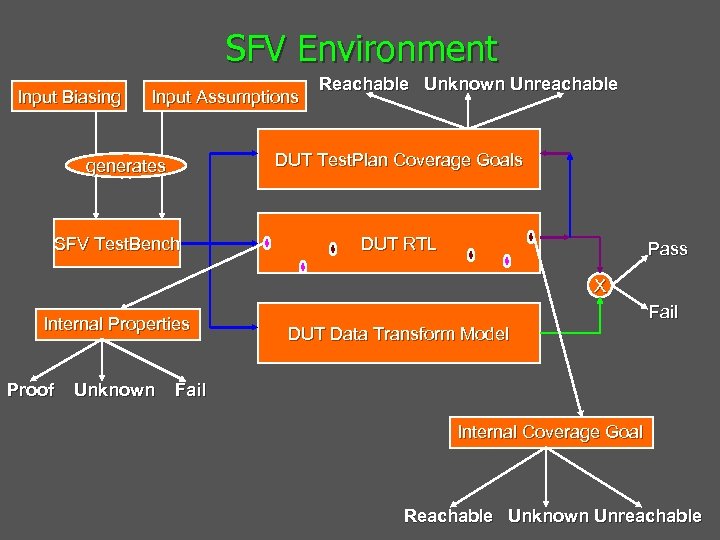SFV Environment Input Biasing Input Assumptions Reachable Unknown Unreachable DUT Test. Plan Coverage Goals generates SFV Test. Bench DUT RTL Pass X Internal Properties Proof Unknown Fail DUT Data Transform Model Fail Internal Coverage Goal Reachable Unknown Unreachable

SFV Environment- Test Bench n Input Assumptions provide legal stimulus n Input Biasing provide higher proportion of important events n Different Random Seeds are applied automatically n Random Simulation obeys Input Assumptions and Biasing n FV obeys Input Assumptions. Biasing is irrelevant n Auto self adjusts user’s biasing to reach coverage goals n Coverage goals missed by SFV are reached by directed testing

Coverage Goals Automated: n Line Coverage n Condition Coverage User Specified: n Implementation Specific n Executable Test Plan

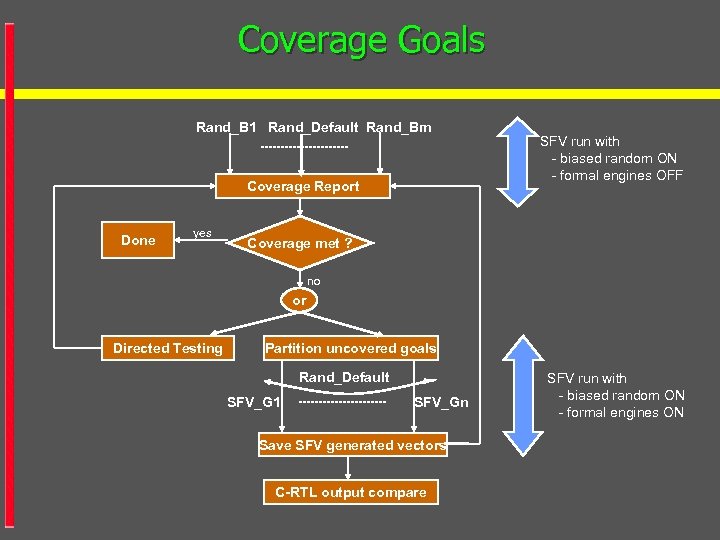Coverage Goals Rand_B 1 Rand_Default Rand_Bm Coverage Report Done yes SFV run with - biased random ON - formal engines OFF Coverage met ? no or Directed Testing Partition uncovered goals Rand_Default SFV_G 1 SFV_Gn Save SFV generated vectors C-RTL output compare SFV run with - biased random ON - formal engines ON

Unit Verification Goals Reached n Coverage goals reached or proved expectedly unreachable n n Line, Condition, User Specified Implementation Specific, User Specified Test Plan n SFV traces that reached above goals = Data Transform Model Output n White Box Properties proved or bounded proved n End to End Data Transport Property proved

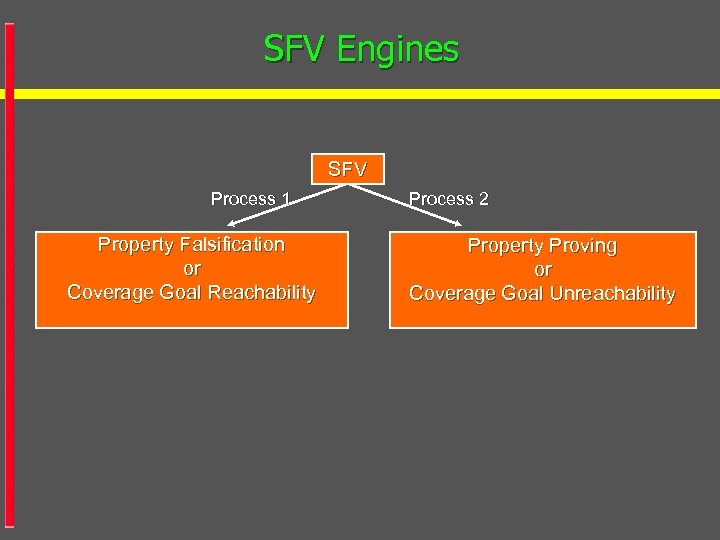SFV Engines SFV Process 1 Property Falsification or Coverage Goal Reachability Process 2 Property Proving or Coverage Goal Unreachability

Using BMC from interesting start states n Default start state is reset state n SFV tool uses heuristics to find interesting start states n User identifies subset of coverage goals as interesting start states n Requires efficient management of the start states population

Helping SFV tool reach interesting states faster n Limiting conditions in DUT may be very “deep” n Tolerable Random Logic Addition to fan-in of internal signals in DUT fifo_full = original_RTL_design_logic || random_hi_or_low; Tout_cntr <= random_decision ? timeout_value : original_RTL_design_logic; n Primarily for finding bugs using SAT n Coverage Goals reached via such techniques are ignored

Enhanced Unit Verification Goals Reached n Coverage goals reached or proved expectedly unreachable n n Line, Condition, User Specified Implementation Specific, User Specified Test Plan n SFV traces that reached above goals = Data Transform Model Output n White Box Properties proved or bounded proved n End to End Data Transport Property proved

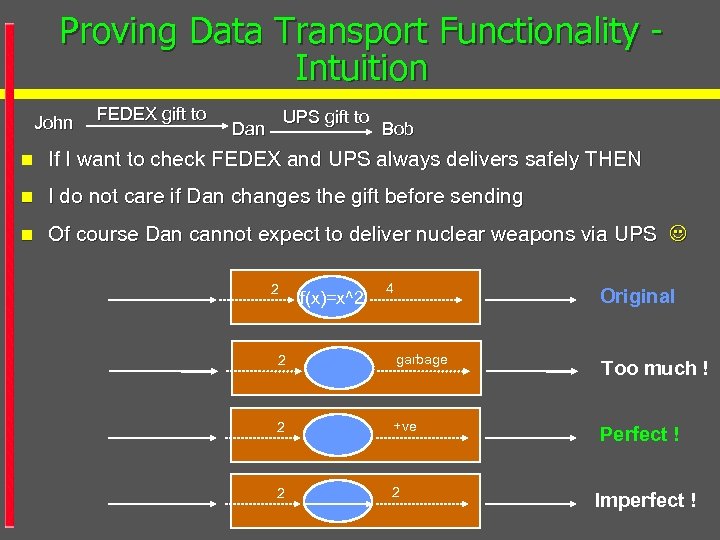Proving Data Transport Functionality Intuition John FEDEX gift to UPS gift to Dan Bob n If I want to check FEDEX and UPS always delivers safely THEN n I do not care if Dan changes the gift before sending n Of course Dan cannot expect to deliver nuclear weapons via UPS 2 f(x)=x^2 4 Original 2 garbage Too much ! 2 +ve Perfect ! 2 2 Imperfect !

Data Transport Properties A packet entering the system may not be visible exiting the system if DUT is viewed as a black box P 1 P 2. . . Pn DUT Q 1 Q 2. . . Qm n >= 1, m >= 0 This happens due to - One or more data transform functions inside DUT or - Legal dropping of a Packet - Single Packet may split to multiple destinations - Multiple Packets may merge to single destination

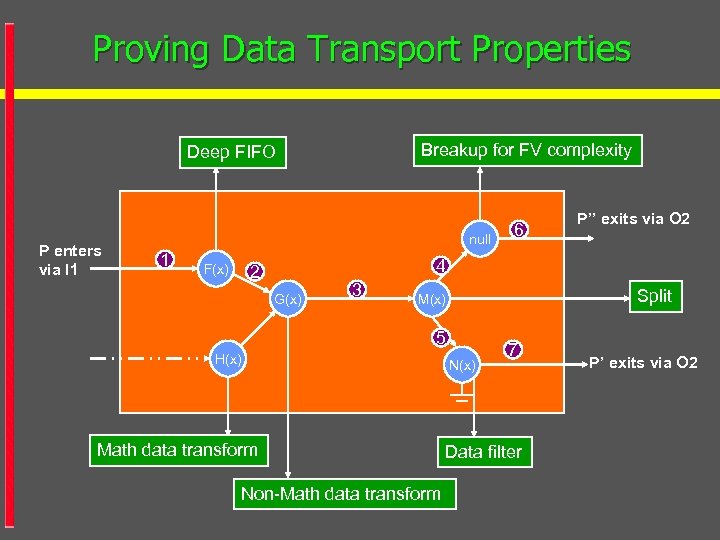Proving Data Transport Properties Breakup for FV complexity Deep FIFO P enters via I 1 null 1 F(x) 6 P’’ exits via O 2 4 2 G(x) 3 Split M(x) 5 H(x) Math data transform Non-Math data transform N(x) 7 Data filter P’ exits via O 2

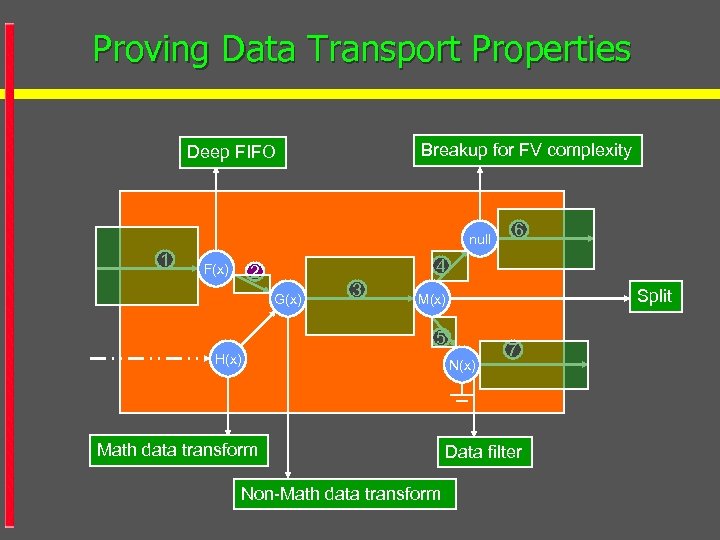Proving Data Transport Properties Breakup for FV complexity Deep FIFO null 1 F(x) 6 4 2 G(x) 3 Split M(x) 5 H(x) Math data transform Non-Math data transform N(x) 7 Data filter

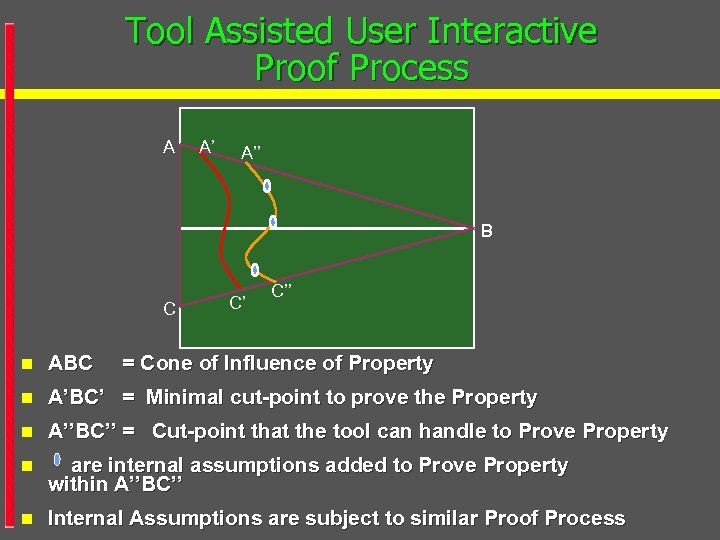Tool Assisted User Interactive Proof Process A A’ A’’ B C C’ C’’ n ABC = Cone of Influence of Property n A’BC’ = Minimal cut-point to prove the Property n A’’BC’’ = Cut-point that the tool can handle to Prove Property n are internal assumptions added to Prove Property within A’’BC’’ n Internal Assumptions are subject to similar Proof Process

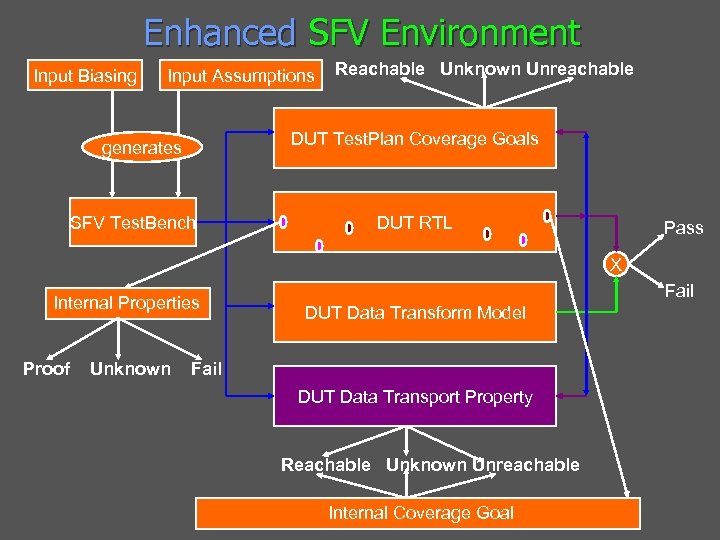Enhanced SFV Environment Input Biasing Input Assumptions Reachable Unknown Unreachable DUT Test. Plan Coverage Goals generates SFV Test. Bench DUT RTL Pass X Internal Properties Proof Unknown Fail DUT Data Transform Model Fail DUT Data Transport Property Reachable Unknown Unreachable Internal Coverage Goal

Enhanced Unit Verification Goals Reached n Coverage goals reached or proved expectedly unreachable n n Line, Condition, User Specified Implementation Specific, User Specified Test Plan n SFV traces that reached above goals = Data Transform Model Output n White Box Properties proved or bounded proved n End to End Data Transport Property proved n Important Properties of Complex Control Logic Blocks proved

Future Improvements n Formal engines parallelized to reach goals faster n Efficient Management of interesting start states population n Automating “logic addition” to DUT to reach bugs faster n Automate Assume Guarantee Verification for proofs