Стратегическое управление портфелем проектов и программой Ч 3

Стратегическое управление портфелем проектов и программой Ч. 3. д. э. н. , проф. В. М. Аньшин Данная презентация не заменяет лекций и является схематичным представлением некоторых вопросов курса

Тема № 2. Основы теории финансового портфеля 1. 2. 3. 4. 5. Основы портфельного анализа Оптимизация портфеля , состоящего из двух активов Допустимое и эффективное множества портфелей Оптимизация портфеля по Марковицу Иммунизация портфеля облигаций

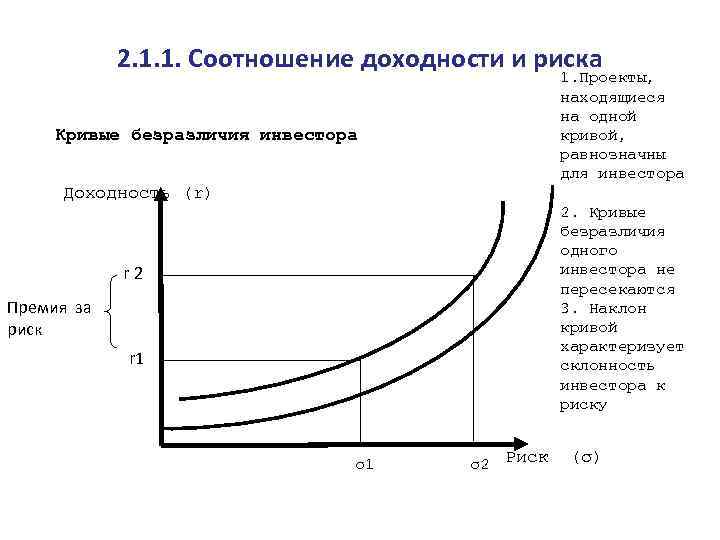2. 1. 1. Соотношение доходности и риска 1. Проекты, находящиеся на одной кривой, равнозначны для инвестора Кривые безразличия инвестора Доходность (r) 2. Кривые безразличия одного инвестора не пересекаются 3. Наклон кривой характеризует склонность инвестора к риску r 2 Премия за риск r 1 σ1 σ2 Риск (σ)

2. 1. 2. Фактическая доходность актива

2. 1. 3. Ожидаемая доходность актива Тогда ожидаемая доходность определится: Если известны доходности по каждому исходу в будущем, то:

2. 1. 4. Дисперсия доходности актива (риск) Расчет дисперсии по прогнозному распределению вероятностей: Расчет дисперсии на основе фактических данных:

2. 1. 5. Доходность портфеля и ковариация активов Фактическая доходность от владения активами за период: или

2. 1. 6. Ковариация и корреляция доходностей активов Ковариация Коэфициент корреляции Сравнив формулы, можно увидеть, что:

2. 1. 7. Дисперсия портфеля i≠j

2. 1. 8. Дисперсия портфеля Адаптируем формулу дисперсии для двух активов: Случай трех активов: необходимо учесть, что σii = 2 σ i

2. 1. 9. Ковариационная матрица Пример. Имеем следующую ковариационную матрицу (величины σij): j i 1 1 2 3 146 187 145 2 187 854 104 3 145 104 289 Допустим, x 1= 0, 2325 x 2= 0, 4070 x 3= 0, 3605

2. 1. 10. Расчет дисперсии портфеля, состоящего из трех активов Найдем дисперсию портфеля:

2. 2. 1. Оптимизация портфеля, состоящего из двух активов rp = r 1 x 1 + r 2 x 2

2. 2. 2. Оптимизация портфеля, состоящего из двух активов На основе данной формулы определяются доли активов в портфеле, обеспечивающие минимальный риск. В зависимости от величины коэффициента корреляции получаем: 1) ρ12 = -1 Подставим данные значения в формулу для вычисления σρ

2. 2. 3. Оптимизация портфеля, состоящего из двух активов 2) ρ12 = 0 В этом случае связь между доходностями активов полностью отсутствует:

2. 2. 4. Оптимизация портфеля, состоящего из двух активов 3) ρ12 = 1 В данном случае имеет место абсолютная положительная взаимосвязь:

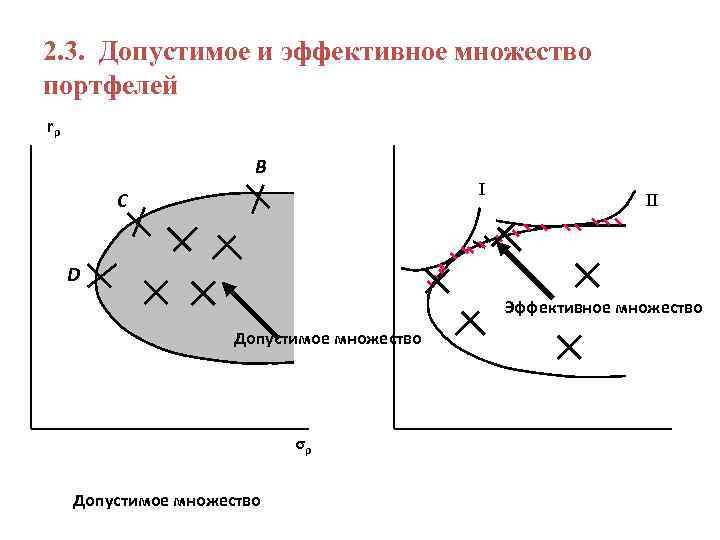2. 3. Допустимое и эффективное множество портфелей rρ B I C II D Эффективное множество Допустимое множество σρ Допустимое множество

2. 4. 1. Оптимизация инвестиционного портфеля по Марковицу

2. 4. 2. Оптимизация инвестиционного портфеля по Марковицу сформируем функцию Лагранжа: где λ – множитель Лагранжа

2. 4. 3. Оптимизация инвестиционного портфеля по Марковицу

2. 4. 4. Оптимизация инвестиционного портфеля по Марковицу Представим систему в матричном виде

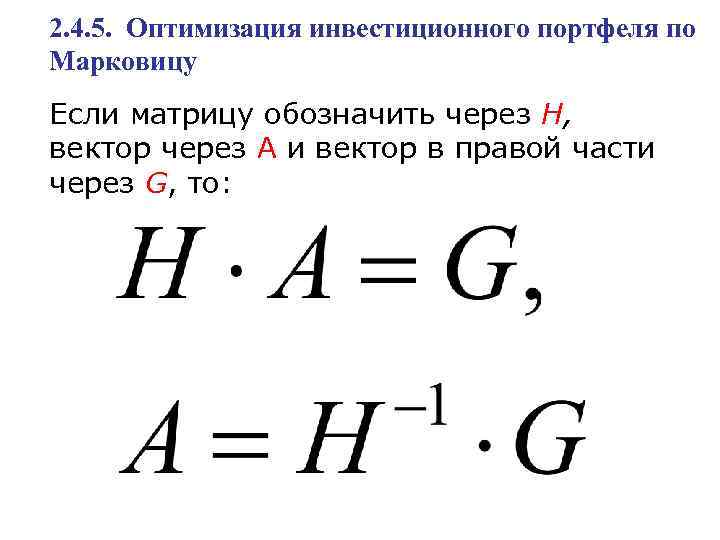2. 4. 5. Оптимизация инвестиционного портфеля по Марковицу Если матрицу обозначить через H, вектор через А и вектор в правой части через G, то:

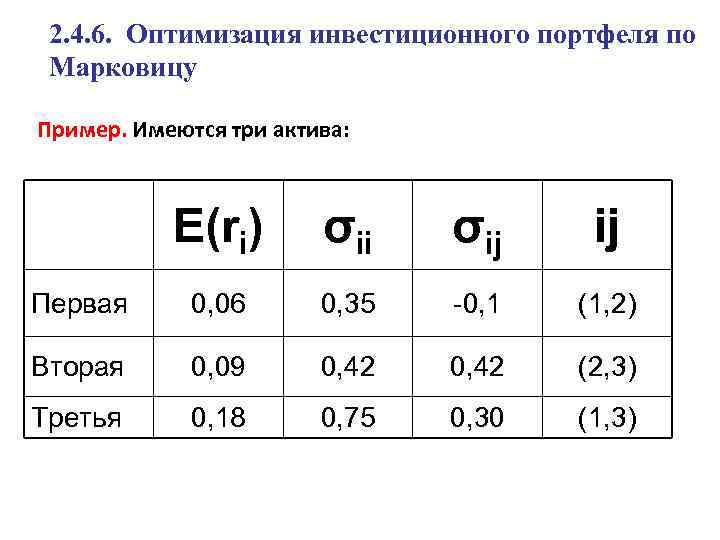2. 4. 6. Оптимизация инвестиционного портфеля по Марковицу Пример. Имеются три актива: E(ri) σii σij ij Первая 0, 06 0, 35 -0, 1 (1, 2) Вторая 0, 09 0, 42 (2, 3) Третья 0, 18 0, 75 0, 30 (1, 3)

2. 4. 7. Оптимизация инвестиционного портфеля по Марковицу

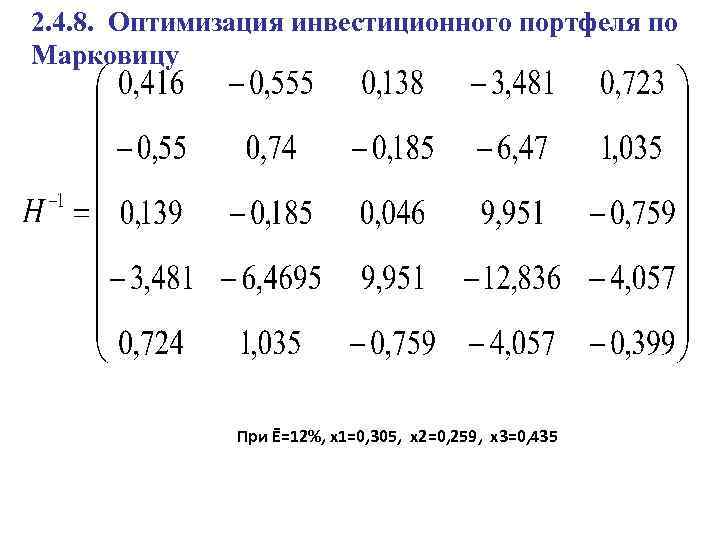2. 4. 8. Оптимизация инвестиционного портфеля по Марковицу При Ē=12%, х1=0, 305, х2=0, 259, х3=0, 435

2. 5. 1. Формирование портфеля облигаций Денежный поток по купонной облигации: -P C 0 год 1 C 2 C 3 C+M n год Денежный поток по бескупонной облигации: M -P 0 n год

2. 5. 2. Показатели доходности облигаций Доходность к погашению:

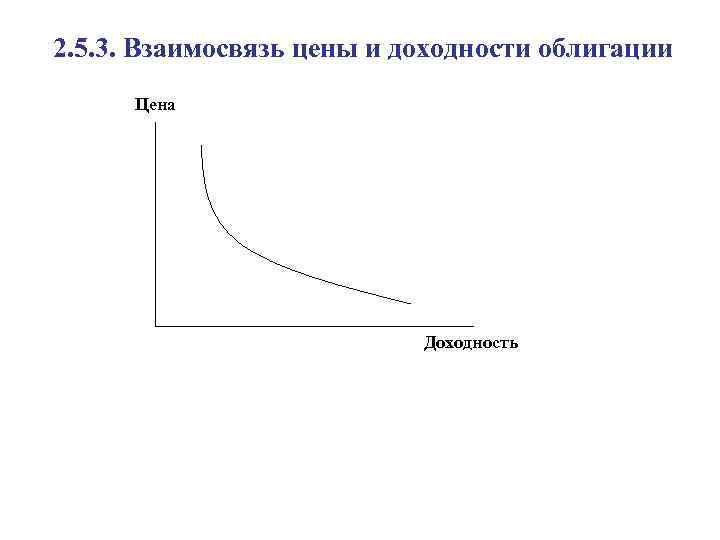2. 5. 3. Взаимосвязь цены и доходности облигации Цена Доходность

2. 5. 4. Дюрация облигации t – срок платежа или элемента ден. потока по облигации CFt – величина элемента ден. потока по облигации в году t r – доходность к погашению

2. 5. 5. Риски облигаций • 1. Кредитный риск –неисполнение эмитентом своих обязательств • 2. Риск реинвестирования – когда период инвестирования больше срока до погашения, возникает вероятность снижения процентной ставки и недополучение запланированного дохода при реинвестировании средств, полученных от погашения облигации • 3. Риск процентной ставки – когда период инвестирования меньше срока до погашения, возникает необходимость продажи облигации на рынке. При увеличении процентной ставки цена может упасть.

2. 5. 6. Иммунизация портфеля облигаций • Портфель облигаций является иммунизированным, если он не восприимчив к изменению процентной ставки (структура портфеля такова, что его стоимость не меняется при изменении процентной ставки). • Портфель облигаций является иммунизированным, если его дюрация равна дюрации(длительности периода) долга (или длительности периода инвестирования)

2. 5. 7. Дюрация и иммунизация портфеля облигаций

Тема № 3. Процессы управления портфелем проектов • 3. 1. Группы процессов управления портфелем проектов • 3. 2. Группа процессов стратегической настройки (выравнивания) • 3. 3. Группа процессов мониторинга и контроля • 3. 4. Управление рисками портфеля проектов