Straight line drawings of planar graphs part

Straight line drawings of planar graphs – part I Roeland Luitwieler

Outline • Introduction • The shift method – The canonical ordering – The shift algorithm • Next time: the realizer method

Introduction • This presentation is about: – Straight line grid drawings of planar graphs – Minimized area • De Fraysseix, Pach & Pollack, 1988: – The shift method: 2 n– 4 x n– 2 grid • Schnyder, 1990: – The realizer method: n– 2 x n– 2 grid • Both are quite different, but can be implemented as linear time algorithms

Introduction • Assumptions (can be taken care of in linear time) – n ≥ 3 (trivial otherwise) – Graph is maximal planar (=triangulated) – Graph has a topological embedding • Terminology – Given an ordering on the vertices of graph G: • Gk is the induced subgraph of vertices v 1, …, vk – Co(G) is the outer cycle of a 2 -connected graph G – Given a cycle C with u and v on it, but (u, v) not on it: • The edge (u, v) is a chord of C

The canonical ordering • An ordering of vertices v 1, …, vn is canonical if for each index k, 3 ≤ k ≤ n: 1. 2. 3. Gk is 2 -connected and internally triangulated (v 1, v 2) is on Co(Gk) If k+1≤n, vk+1 is in the exterior face of Gk and its neighbours in Gk appear on Co(Gk) consecutively

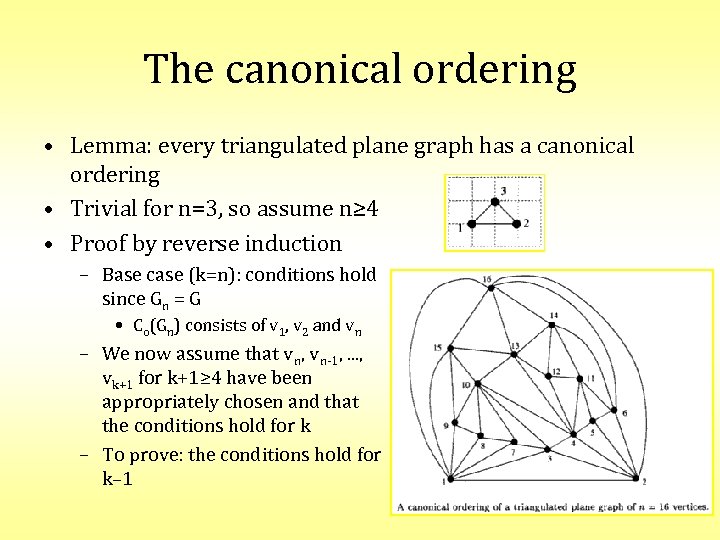The canonical ordering • Lemma: every triangulated plane graph has a canonical ordering • Trivial for n=3, so assume n≥ 4 • Proof by reverse induction – Base case (k=n): conditions hold since Gn = G • Co(Gn) consists of v 1, v 2 and vn – We now assume that vn, vn-1, . . . , vk+1 for k+1≥ 4 have been appropriately chosen and that the conditions hold for k – To prove: the conditions hold for k– 1

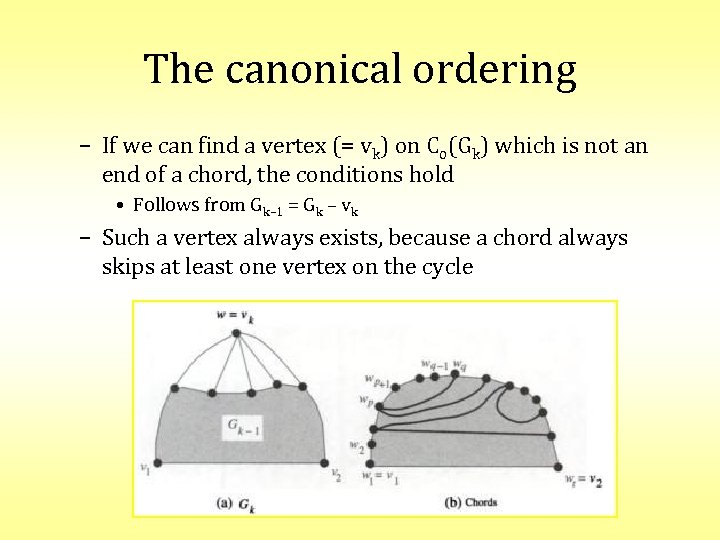The canonical ordering – If we can find a vertex (= vk) on Co(Gk) which is not an end of a chord, the conditions hold • Follows from Gk– 1 = Gk – vk – Such a vertex always exists, because a chord always skips at least one vertex on the cycle

The canonical ordering • A canonical ordering of a triangulated plane graph can be found in linear time – Use labels for vertices • Label -1 means not yet visited • Label 0 means visited once • Label i means visited more than once and there are i intervals of visited neighbours in the circular order around the vertex – Algorithm: • Let v 1 and v 2 be two consecutive vertices on Co(G) in counter clockwise order • Label all other vertices -1 • Process v 2 • for k = 3 to n do – Chose a vertex v with label 1 – vk = v – Process vk

The canonical ordering – (Sub-algorithm) Process v: • For all neighbours w of v not yet processed do – If label -1 then label(w) = 0 – If label 0 then (w has one processed neighbour u) » If w next to u in circular order of neighbours of v then label(w) =1 » Otherwise label(w) = 2 – Otherwise (label i) » If vertices next to w in circular order of neighbours of v both have been processed then label(w) = i– 1 » If neither has been processed yet then label(w) = i+1 – Correctness • All processed vertices form Gk and the chosen vertex is vk+1 – Verify the conditions hold now • Successful termination guaranteed by previous proof

The shift algorithm • General idea: – Insert vertices in canonical order in drawing – Invariants when inserting vk: 1. x(v 1) = 0, y(v 1) = 0, x(v 2) = 2 k– 6, y(v 2) = 0 2. x(w 1) < … < x(wt) where Co(Gk– 1) = w 1, …, wt with w 1 = v 1, wt = v 2 3. Each edge on Co(Gk– 1) except (v 1, v 2) is drawn by a straight line having slope +1 or – 1

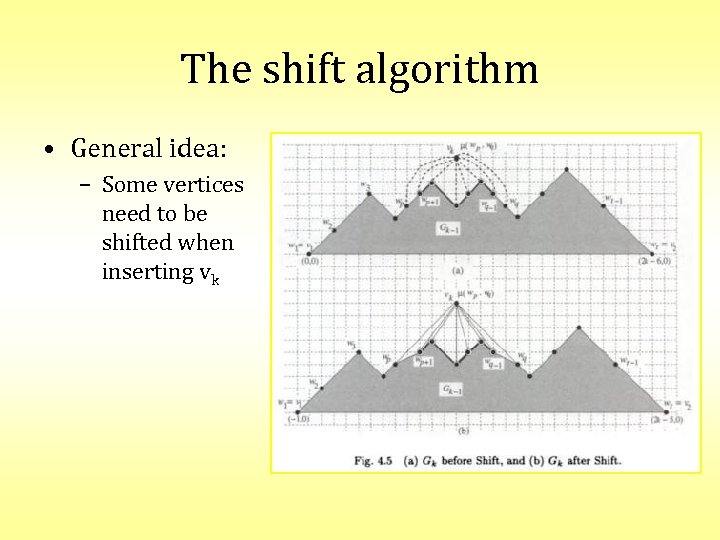The shift algorithm • General idea: – Some vertices need to be shifted when inserting vk

The shift algorithm • To obtain a linear time algorithm, x-offsets are used in stead of x-coordinates • We use a binary tree to represent shift dependencies – Each node shifts whenever its parent shifts – Store x-offset and y-coordinate in each node • Using the tree, the x-offsets can be accumulated in linear time

The shift algorithm • Compute x-offsets and y-coordinates: – Compute values and create the tree for G 3 – For k = 4 to n do • • • Let w 1, …, wt = Co(Gk– 1) with w 1 = v 1, wt = v 2 Let wp, wp+1, …, wq be the neighbours of vk on Co(Gk– 1) Increase Δx(wp+1) and Δx(wq) by one Compute Δx(vk) and y(vk) Update the tree accordingly

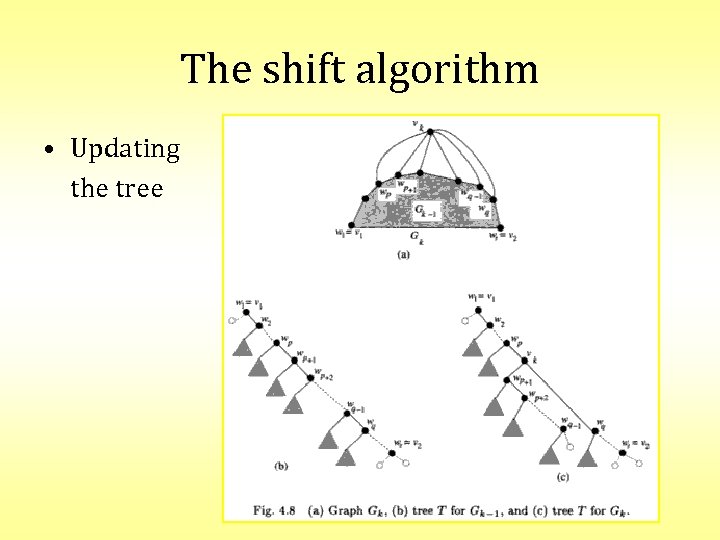The shift algorithm • Updating the tree

The shift algorithm • Computing Δx(vk) and y(vk) – Δx(wp, wq) = Δx(wp+1) +. . . + Δx(wq) – Δx(vk) = ½ {Δx(wp, wq) + y(wq) – y(wp)} – y(vk) = ½ {Δx(wp, wq) + y(wp)} – Other necessary updates: • Δx(wq) = Δx(wp, wq) – Δx(vk) • If p+1 <> q then Δx(wp+1) = Δx(wp+1) – Δx(vk)

Conclusions • The shift method uses – The canonical ordering – A 2 n– 4 x n– 2 grid, obviously – Linear time • Next time: the realizer method • Questions?

References • H. de Fraysseix, J. Pach and R. Pollack, How to draw a planar graph on a grid, Combinatorica 10 (1), 1990, pp. 41– 51. • D. Harel and M. Sardas, An Algorithm for Straight-Line Drawing of Planar Graphs, Algorithmica 20, 1998, pp. 119– 135. • T. Nishizeki and Md. S. Rahman, Planar Graph Drawing, World Scientific, Singapore, 2004, pp. 45– 88. • W. Schnyder, Embedding planar graphs on the grid, in: Proceedings of the First ACM-SIAM Symposium on Discrete Algorithms, 1990, pp. 138– 148.