Лекция 6 - Стохастические сети.ppt
- Количество слайдов: 33

Стохастические сети массового обслуживания и их параметры Лекция 6

Определение сети массового обслуживания (Ст. МО) Ст. МО или стохастическая сеть – это совокупность взаимосвязанных СМО. Примеры реальных обьектов, описываемых Ст. МО: (заявка при обслуживании проходит несколько СМО последовательно, прежде чем покинуть этот объект ) • покупатель в универмаге, • документ в министерстве, • деталь при последовательной обработке, • программа в компьютере … Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 2
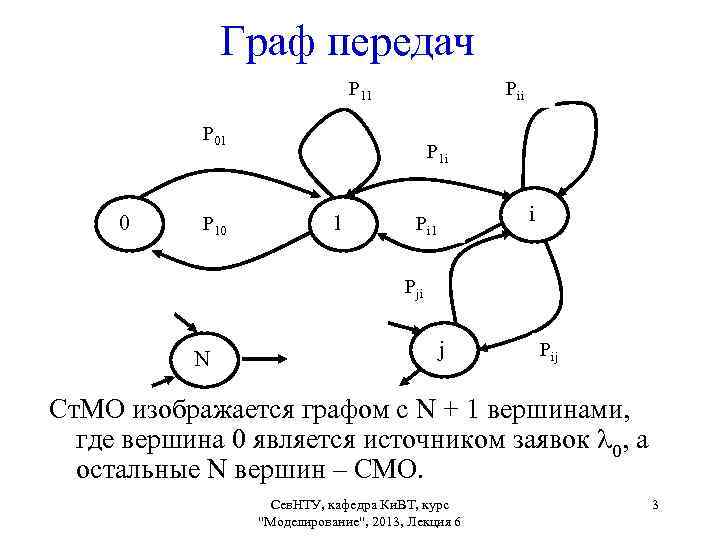
Граф передач Р 11 Рii Р 01 0 Р 1 i 1 Рi 1 i Рji N j Рij Ст. МО изображается графом с N + 1 вершинами, где вершина 0 является источником заявок 0, а остальные N вершин – СМО. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 3

Характеристики СМО в составе Ст. МО Каждая СМО j характеризуется: 1) числом Кj каналов обслуживания 2) временем j обслуживания в канале Заявка из источника с вероятностью Р 0 j может поступить в СМО j. Выходя из i-й СМО, заявка с вероятностью Рij может поступить в j-ю СМО, j = 0, 1, …, N. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 4

Матрица вероятностей передач Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 5
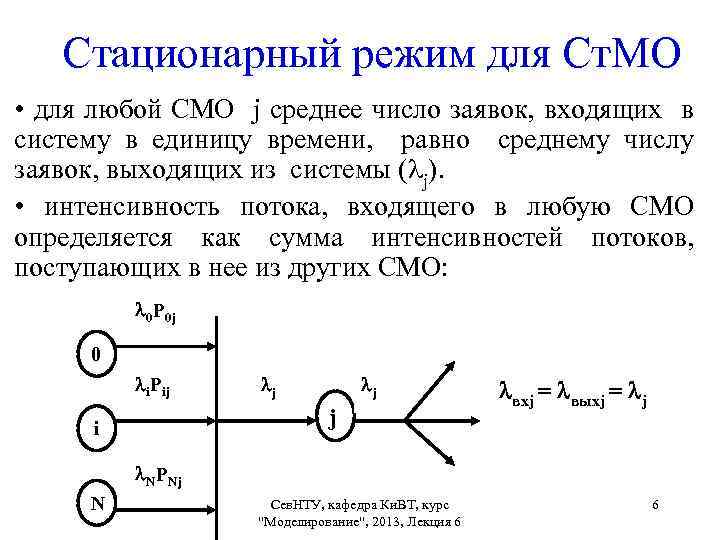
Стационарный режим для Ст. МО • для любой СМО j среднее число заявок, входящих в систему в единицу времени, равно среднему числу заявок, выходящих из системы ( j). • интенсивность потока, входящего в любую СМО определяется как сумма интенсивностей потоков, поступающих в нее из других СМО: 0 P 0 j 0 i. Pij j j j i вхj = выхj = j NPNj N Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 6

Уравнения для определения интенсивностей потоков заявок Решая эту систему, получим выражения вида j - коэффициент передачи – он характеризует долю заявок, поступающих в j-й узел от источника заявок, либо - среднее число прохождений какой-либо заявки через СМО j в процессе обслуживания. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 7
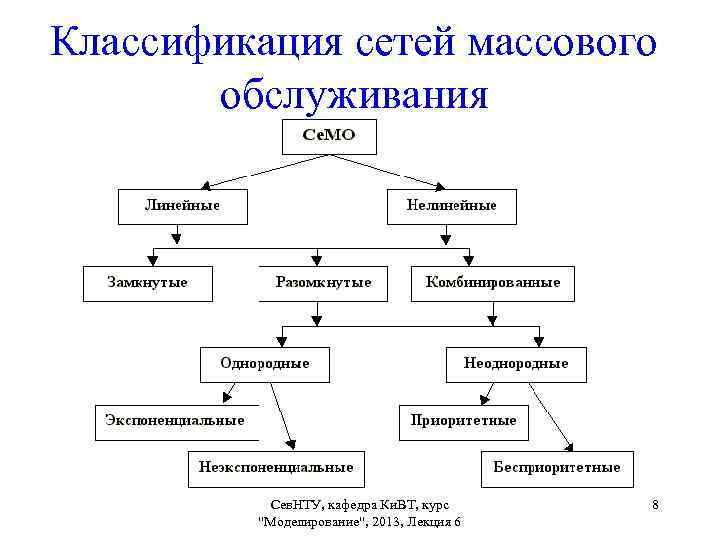
Классификация сетей массового обслуживания Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 8

Разомкнутые Ст. МО называется открытой или разомкнутой, если интенсивность источника не зависит от числа заявок, находящихся в сети. Разомкнутые Ст. МО применяются в качестве моделей систем, в которых находится переменное число заявок – вычислительных систем с разделением времени. Заявки – запросы со стороны пользователя на выполнение отдельных работ. Для разомкнутых Ст. МО известна интенсивность источника заявок 0 – система (1) имеет единственное решение вида (2). Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 9
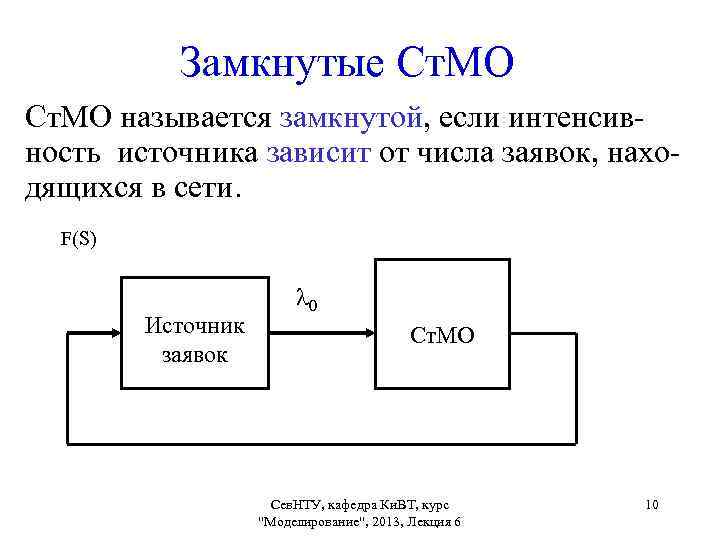
Замкнутые Ст. МО называется замкнутой, если интенсивность источника зависит от числа заявок, находящихся в сети. F(S) Источник заявок 0 Ст. МО Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 10

Замкнутые Ст. МО В пределе в замкнутой Ст. МО может циркулировать постоянное число М заявок. В этом случае источник, в который поступает заявка, немедленно генерирует новую, так что в сети постоянно находится одно и то же число заявок. Для замкнутых Ст. МО ни одна из интенсивностей заранее не известна - система (1) имеет бесконечное множество решений. Возможно определить коэффициенты передач путем решения системы (1), в которую подставляется значение 0 = 1. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 11

Применение замкнутых Ст. МО Описание работы таких систем, в которых ведется обработка фиксированного числа заявок: 1) система оперативной обработки, функционирующая в диалоговом режиме - имеется фиксированное число пользователей, каждый из которых не инициирует новый запрос к системе до тех пор, пока не будет получен ответ на предшествующий запрос. 2) система с пакетной обработкой - количество заявок, циркулирующих в сети, определяется количеством задач, выполняющихся в мультипрограммном режиме ( коэффициентом мультипрограммирования). Когда выполнение работ заканчивается, инициируется новая работа, выбираемая из входного пакета. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 12
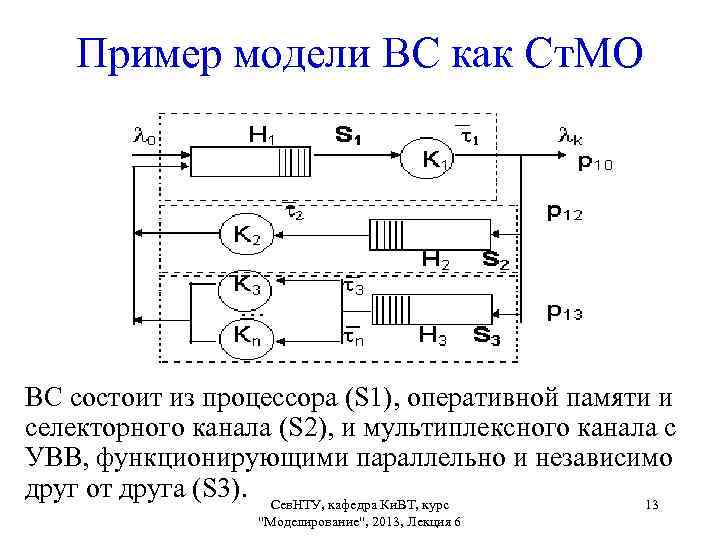
Пример модели ВС как Ст. МО ВС состоит из процессора (S 1), оперативной памяти и селекторного канала (S 2), и мультиплексного канала с УВВ, функционирующими параллельно и независимо друг от друга (S 3). Сев. НТУ, кафедра Ки. ВТ, курс 13 "Моделирование", 2013, Лекция 6

Пример модели ВС как Ст. МО S 1, S 2, S 3 - СМО, отображающие этапы обработки задач в подсистеме процессор - оперативная память - селекторный канал - мультиплексный канал. Момент начала решения задачи отмечается поступлением заявок. Заявки воспринимаются процессором (S 1) и начинают выполнение определенных операций в соответствии с программой. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 14

Пример модели ВС как Ст. МО Процесс выполнения программы можно рассматривать как процесс выполнения различных этапов: Þ счет, Þ обращение к ВЗУ, Þ ввод - вывод информации через УВВ. После выполнения некоторой последовательности таких этапов, число которых зависит от трудоемкости самой программы, заявки могут покидать систему. Процесс решения задачи носит многоэтапный характер и складывается из периодической работы процессора, селекторного канала, мультиплексного канала. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 15

Пример модели ВС как Ст. МО В сетевых моделях этот процесс отмечается как циркуляция заявок в сети : S 1 S 2, S 1 S 3, Переход заявок в систему S 2 или S 3 может осуществляться только лишь из устройства S 1, так как заявки на ввод/вывод формируются программами, обрабатываемыми процессором. Заявки после обработки в процессоре S 1 могут попадать с вероятностью р12 и р13 соответственно в системы S 2 и S 3, после нескольких циклов обслуживания с вероятностью р10 заявки покидают систему. Интенсивность выходящего потока равна k, так как вычислительная система работает без потерь заявок, то k= 0. Сев. НТУ, кафедра Ки. ВТ, курс 16 "Моделирование", 2013, Лекция 6
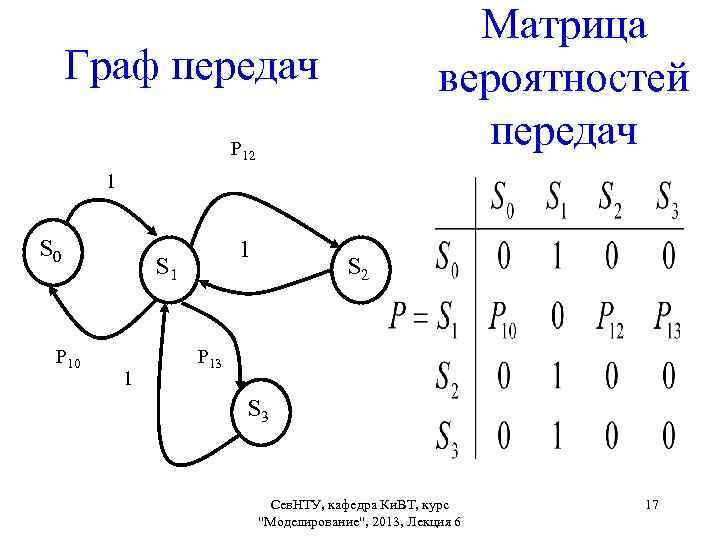
Матрица вероятностей передач Граф передач Р 12 1 S 0 Р 10 1 S 1 1 S 2 Р 13 S 3 Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 17

Определение интенсивностей и коэффициентов передач Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 18

Разомкнутые стохастические сети и их характеристики

Параметры разомкнутой сети 1) N – число СМО, образующих сеть; 2) 0 – интенсивность потока заявок на выходе источника S 0; 3) матрица вероятностей передач где Рij - вероятность того, что заявка из системы Si направляется в Sj. 4) Каждая СМО i характеризуется Кi - числом каналов обслуживания i - средним временем обслуживания в канале. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 20

Характеристики в стационарном режиме Узловые характеристики: Li, mi, wi и ui – для всех систем (узлов) Si, i=1, …, n. Сетевые характеристики: 1) L - средняя суммарная длина очередей, 2) m - среднее число заявок, пребывающих в сети, 3) w - среднее время ожидания заявки в очередях, 4) u – среднее время пребывания заявки в Ст. МО. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 21

Условие существования стационарного режима Требование одновременности выполнения условий стационарности для всех узлов сети: Ri < Ki , i = 1, . . . , n, или, учитывая, что Ri = i 0 i Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 22

Экспоненциальная стохастическая сеть Стохастическая Ст. МО называется экспоненциальной, если • поток заявок от источника – простейший • времена обслуживания во всех узлах сети распределены по экспоненциальному закону. В этом случае Ст. МО ведет себя как совокупность n независимых СМО типа М/М/Кi/ Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 23

Узловые характеристики экспоненциальной разомкнутой сети 1) Средняя длина очереди 2) Вероятность простоя Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 24

Узловые характеристики экспоненциальной разомкнутой сети 3) Средняя загрузка одного канала 4) Полная загрузка узла (СМО) В стационарном режиме Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 25

Узловые характеристики экспоненциальной разомкнутой сети 5) Среднее число заявок в узле 6) Среднее время ожидания заявки в очереди 7) Среднее время пребывания заявки в узле Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 26

Узловые характеристики экспоненциальной разомкнутой сети Для случая Ki =1, i = 1, . . . , n (Все СМО одноканальные) Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 27

Пример модели ВС как Ст. МО Найти значение критерия эффективности вида: где еож - штраф за единицу времени ожидания заявки в очередях; е. Нi - штраф за недоиспользование каналов в системе Si, i = 1, . . . , n. еож = 10 у. е. /канал; е. Н 1 = 20 у. е. /канал; е. Н 2 = 10 у. е. /канал; е. Н 3 = 2 у. е. /канал. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 28

Пример модели ВС как Ст. МО Параметры Ст. МО следующие: 1) число СМО n = 3; 2) число каналов обслуживания К 1 = 1; К 2 = 1; К 3 = 2; 3) средние времена обслуживания 1 = 0, 5 с; 2 = 1, 25 с; 3 = 10 с. 4)интенсивность источника 0 = 0, 02 c-1 5 ) Коэффициенты передачи 1 = 10; 2 = 4; 3 = 5. Сев. НТУ, кафедра Ки. ВТ, курс 29 "Моделирование", 2013, Лекция 6

Пример модели ВС как Ст. МО Условие существования стационарного режима: 0 = 0. 02 < 0. 04 - стационарный режим существует Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 30

Характеристики Ст. МО 1) Интенсивности входящих потоков 1 = 1 0 = 10 * 0, 02 = 0, 2 с-1 2 = 2 0 = 4 * 0, 02 = 0, 08 с-1 3 = 3 0 = 5 * 0, 02 = 0, 1 с-1 2) Среднее число занятых каналов R 1 = 1 1 = 0, 2 * 0, 5 = 0, 1 R 2 = 2 2 = 0, 08 * 1, 25 = 0, 1 R 3 = 3 3 = 0, 1 * 10 = 1 3) Средняя загрузка одного канала 1 = R 1 / K 1 = 0, 1 2 = R 2 / K 2 = 0, 1 3 = R 3 / K 3 = 0, 5 Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 31

Средние времена пребывания в очереди Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 Р 03 = 0. 33 L 3 = 3. 33 w 3 = 33. 3 32

Среднее время ожидания заявки в очередях: Значение критерия эффективности Е = 10 * 167. 62 + 20 (1 – 0. 1) + 10 (1 – 0. 1) + + 2 (2 - 1) = 1705. 2 у. е. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 6 33
Лекция 6 - Стохастические сети.ppt