Стохастические модели Виды стохастических моделей Стохастические модели

Стохастические модели

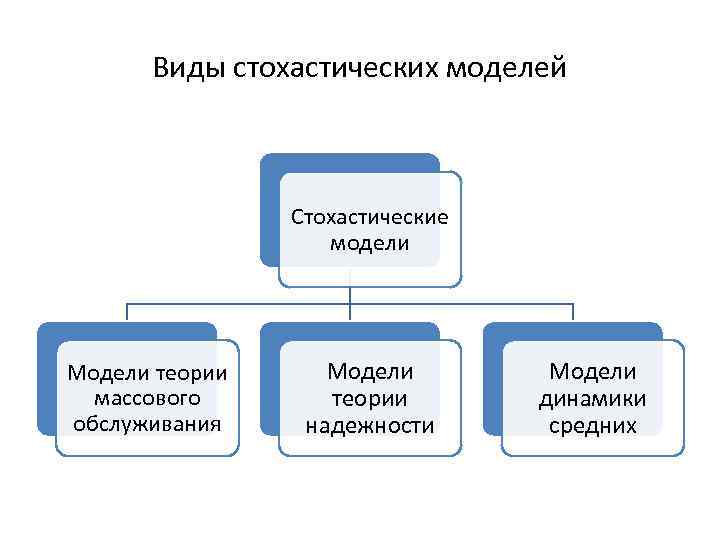Виды стохастических моделей Стохастические модели Модели теории массового обслуживания Модели теории надежности Модели динамики средних

Стохастические и имитационные модели Стохастические модели • Модели теории массового обслуживания • Модели теории надежности • Модели динамики средних Имитационные модели • Дискретнособытийные модели • Агентные модели • Модели системной динамики

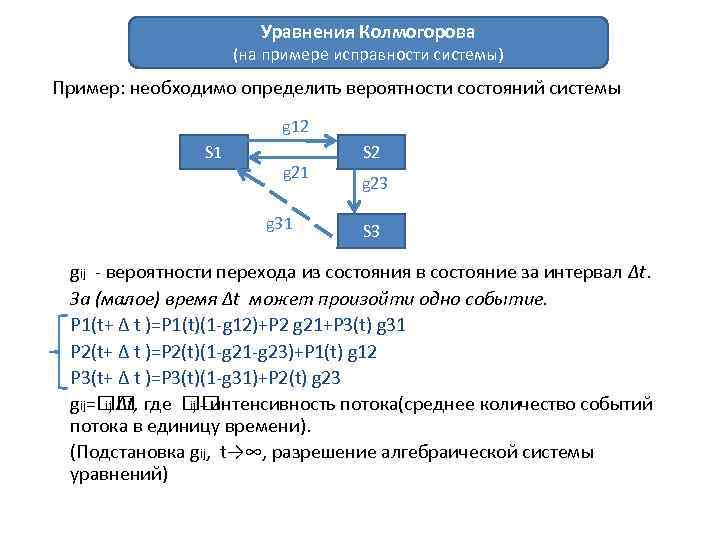Уравнения Колмогорова (на примере исправности системы) Пример: необходимо определить вероятности состояний системы g 12 S 1 g 21 g 31 S 2 g 23 S 3 gij - вероятности перехода из состояния в состояние за интервал Δt. За (малое) время ∆t может произойти одно событие. P 1(t+ ∆ t )=P 1(t)(1 -g 12)+P 2 g 21+P 3(t) g 31 P 2(t+ ∆ t )=P 2(t)(1 -g 23)+P 1(t) g 12 P 3(t+ ∆ t )=P 3(t)(1 -g 31)+P 2(t) g 23 gij= где ij ∆t, ij – интенсивность потока(среднее количество событий потока в единицу времени). (Подстановка gij, t→∞, разрешение алгебраической системы уравнений)

Основные определения и понятия ТМО Поток событий – процесс, в котором повторяются однородные события (случайным является время между событиями). Особую роль среди всех потоков играет Пуассоновский простейший поток. Ординарный поток – это поток, для которого вероятность появления более одного события за интервал времени ∆ t есть o(Р(1)) при ∆t 0. (Пример: фотофиниш. Т. о. фактически нет событий происходящих одновременно). Стационарный поток – это поток, для которого появление k событий за интервал ∆ t зависит только от длины этого интервала и не зависит от момента начала этого интервала. Поток без последействия – это поток, для которого вероятность появления k событий за интервал ∆ t не зависит от количества событий потоков за время, предшествующее данному интервалу.

Основные определения и понятия ТМО Простейший поток – это поток ординарный, стационарный и баз последействия (Марковский процесс). Пуассоновский поток – вероятность возникновения события за интервал ∆ t подчиняется распределению Пуассона: Интервал времени между событиями потока имеет плотность: Пуассоновского потока (как и нормального распределения) в чистом виде в природе и на практике не существует. Является предельным потоком, который возникает как результирующий поток, порождаемый большим количеством причин.

Системы массового обслуживания СМО – это любая система, в которой поток требований, сталкивается с ограниченными ресурсами для их выполнения (например, конвейер, дорога, завод и т. п. ). Все методы ТМО направлены на выбор оптимальных параметров СМО (при учёте случайных факторов). Происходит исследование: как параметры СМО влияют на показатели её работы. В основе лежит поток случайных событий!

Описание СМО А/В/N/M/K, где А - распределение времени входного потока заявок; В - распределение времени обслуживания заявок; N - количество обслуживающих приборов; М - количество мест в очереди; К - количество источников заявок. Типовые обозначения (стоят в формуле вместо А и В): • М – Пуассоновское распределение (показательное распределение времени между событиями потока; • Er – распределение Эрланга порядка r; • Hr – гипергеометрическое распределение порядка r; • D - детерминированное распределение; • G - распределение произвольного вида.

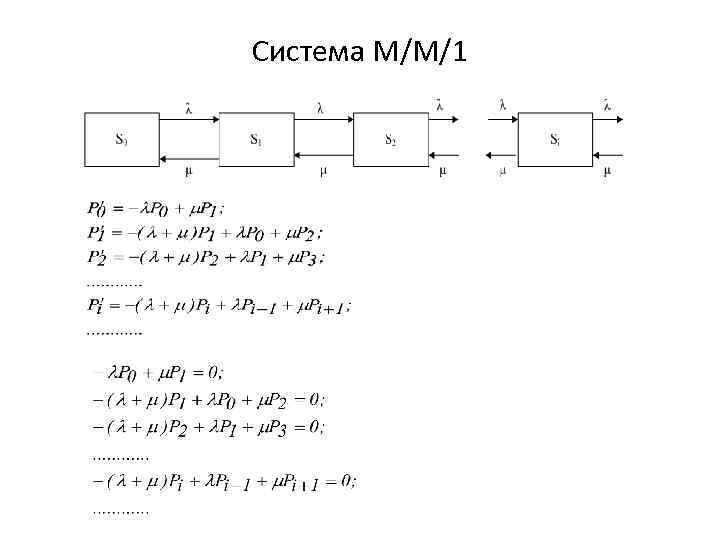Система М/М/1

Система М/М/1 (продолжение)

Основные характеристики СМО • Абсолютная пропускная способность системы, т. е. количество заявок, обслуживаемых системой в единицу времени; • Относительная пропускная способность или средняя доля обслуживаемых заявок (отношение количества заявок, обслуженных за интервал времени, к количеству заявок, поступивших в СМО за тот же интервал времени); • Среднее число занятых обслуживающих приборов; • Среднее относительное время простоя системы в целом и отдельного прибора; • Среднее число заявок в очереди; • Среднее число заявок в системе (на обслуживании и в очереди); • Среднее время пребывания заявки в системе (в очереди и на обслуживании); • Среднее время ожидание заявкой обслуживания.

Основные функциональные характеристики СМО • Абсолютная пропускная способность системы, т. е. количество заявок, обслуживаемых системой в единицу времени; • Относительная пропускная способность или средняя доля обслуживаемых заявок (отношение количества заявок, обслуженных за интервал времени, к количеству заявок, поступивших в СМО за тот же интервал времени); • Среднее число занятых обслуживающих приборов; • Среднее относительное время простоя системы в целом и отдельного прибора; • Среднее число заявок в очереди; • Среднее число заявок в системе (на обслуживании и в очереди); • Среднее время пребывания заявки в системе (в очереди и на обслуживании); • Среднее время ожидание заявкой обслуживания

Некоторые соотношения для основных функциональных характеристик Формула Литтла Система М/М/1 • Абсолютная пропускная способность системы А=λq=λ • Относительная пропускная способность q=1 • Среднее число занятых обслуживающих приборов ρ • Среднее относительное время простоя системы 1 - ρ • Среднее число заявок в очереди • Среднее число заявок в системе • Среднее время пребывания заявки в системе • Среднее время ожидание заявкой обслуживания

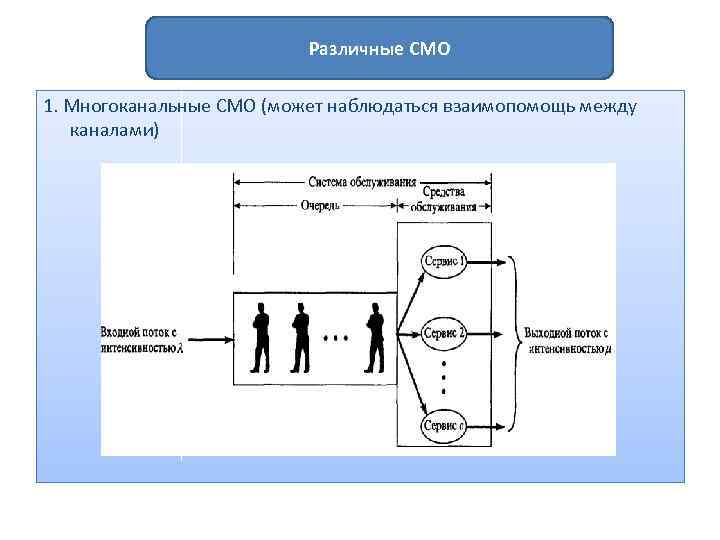Различные СМО 1. Многоканальные СМО (может наблюдаться взаимопомощь между каналами)

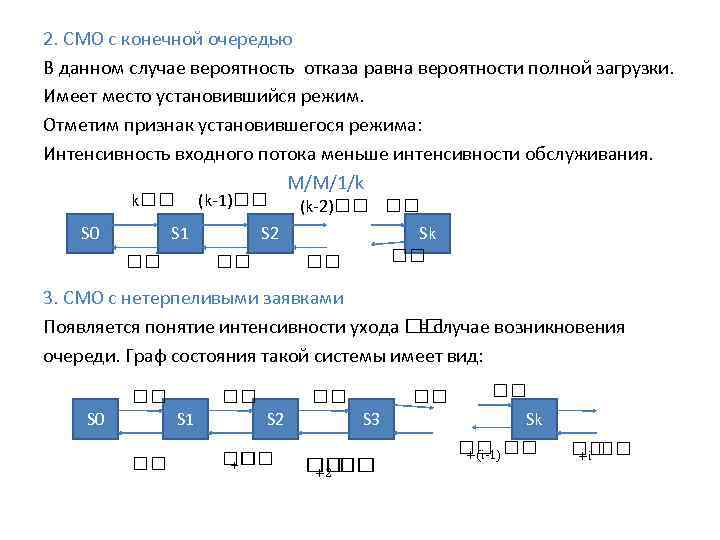2. СМО с конечной очередью В данном случае вероятность отказа равна вероятности полной загрузки. Имеет место установившийся режим. Отметим признак установившегося режима: Интенсивность входного потока меньше интенсивности обслуживания. M/M/1/k k S 0 (k-1) S 1 (k-2) S 2 Sk 3. СМО с нетерпеливыми заявками Появляется понятие интенсивности ухода в случае возникновения очереди. Граф состояния такой системы имеет вид: S 0 S 1 S 2 + S 3 +2 Sk +(i-1) +i

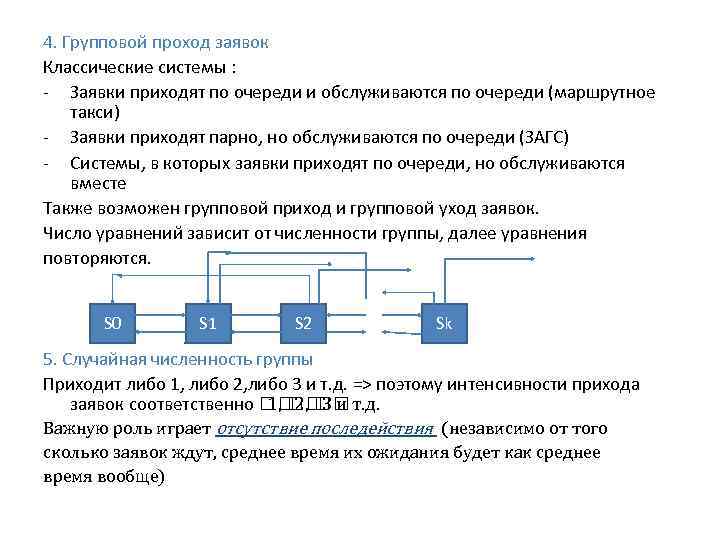4. Групповой проход заявок Классические системы : - Заявки приходят по очереди и обслуживаются по очереди (маршрутное такси) - Заявки приходят парно, но обслуживаются по очереди (ЗАГС) - Системы, в которых заявки приходят по очереди, но обслуживаются вместе Также возможен групповой приход и групповой уход заявок. Число уравнений зависит от численности группы, далее уравнения повторяются. S 0 S 1 S 2 Sk 5. Случайная численность группы Приходит либо 1, либо 2, либо 3 и т. д. => поэтому интенсивности прихода заявок соответственно 2, т. д. 1, 3 и Важную роль играет отсутствие последействия (независимо от того сколько заявок ждут, среднее время их ожидания будет как среднее время вообще)

Анализ неклассических СМО (непуассоновских) Метод Этапов 2 2 Состояния системы – это количество всех этапов обслуживания, которые необходимо пройти всем заявкам, находящимся в системе Распределение событий (распределение Эрланга), является более регулярным, чем распределение Пуассона. Гипергеометрическое распределение является менее регулярным. Преобразование этапов приводит к преобразованию вида : P(S)/Q(S) Метод вложенных цепей Маркова Из исходных случайных событий процесса выбираются такие, в которых состояния процесса образуют Марковскую цепь. Затем применяются обычные методы теории Марковских цепей для тех характерных моментов времени(случайных моментов) , в которых процессы являются Марковскими. Марковский процесс имеет место в том случае, если состояние системы в будущем определяется лишь текущим состоянием и не зависит от предыдущего состояния. Для немарковских случайных процессов ищется последовательность моментов, в которых процесс является Марковским, затем находим распределение вероятностей состояний цепи и по нему восстанавливаем распределение для исходного немарковского процесса Метод диффузионных приближений Используется уравнение Фоккера-Планка-Колмогорова (уравнение в частных производных) Решением будет функция , а не число Одна переменная берётся дискретной, например количество заявок, а другая непрерывной, например время Метод Монте-Карло (статистические испытания) Моделирование процессов, где случайные факторы заменяются на их реализации. Необходимо знать функцию распределения вероятности F(x)=P(X

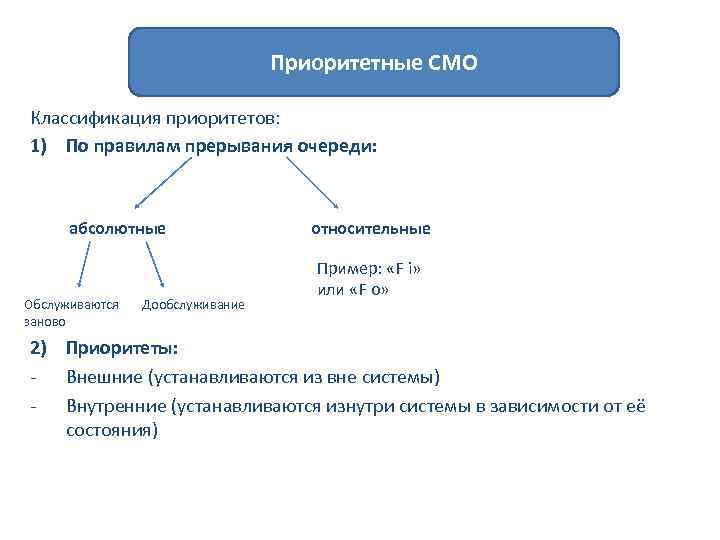Приоритетные СМО Классификация приоритетов: 1) По правилам прерывания очереди: абсолютные Обслуживаются заново Дообслуживание относительные Пример: «F i» или «F o» 2) Приоритеты: - Внешние (устанавливаются из вне системы) - Внутренние (устанавливаются изнутри системы в зависимости от её состояния)

Сети массового обслуживания

Сети массового обслуживания Признак классификации По виду входящих в сеть СМО Классы моделей Марковские Немарковские Смешанные, приоритетные, т. д. По способу обмена заявками с внешней Замкнутые средой Разомкнутые Смешанные Интенсивности, зависящие от количества и/или распределения заявок в сети По времени и способу перемещения заявок между системами сети Мгновенное Конечное (детерминированное, случайное) Циклические и ациклические сети По гибкости структуры сети Сети с постоянной структурой Сети с управляемой структурой (производительностью СМО)