Столица Татарстана — г. Казань, приветствует ВАС!

Столица Татарстана - г. Казань, приветствует ВАС! Исанмесез! Дата рождения города относится к далекому ХI веку. Тогда это была небольшая пограничная крепость мощного государства Волжская Булгария. Город возник на стрелке высокого холма, который с трех сторон был окружен водой. Башня Сююмбеки Мечеть Кул-Шериф

Министерство образования и науки РФ Казанский государственный архитектурно-строительный университет Кафедра начертательной геометрии и графики

учебная дисциплина «ИНЖЕНЕРНАЯ ГРАФИКА»

Артюхин Георгий Алексеевич (Казанский государственный архитектурно-строительный университет) в стиле презентации предлагает курс лекций по дисциплине: «Инженерная графика»

Цель - повышение качества образования

- Научить правилам чтения и составления чертежа - Привить навыки работы с чертежными инструментами - Научить создавать геометрические модели пространственных объектов и их проекций на компьютере

Как при такой рабочей программе подготовить будущего инженера? Распределение времени по учебному плану: Всего на дисциплину: …………………. 110 часов первый семестр: ……………………. 48 часов второй семестр: ……………………… 62 часа Ответ: Аудиторные занятия (всего): ……………… 32 часа посредством 1 семестр: 32 часа (лекции: 16 часов, практические занятия: 16 часов) дополнения 2 семестр: 32 часа (лабораторные занятия: 16 часов, классической практические занятия: 16 часов) формы Самостоятельная работа: …………………. . 58 часов литературы первый семестр: ………………………. 30 часов «электронными второй семестр: ………………………. . 28 часов версиями» Вид промежуточной аттестации: первый семестр экзамен второй семестр зачёт

Введение. Графическая информация является средством общения во всех сферах деятельности человека. Учебная дисциплина «Инженерная графика» призвана привить студентам инженерных вузов навыки работы с графической информацией любой сложности, начиная от традиционного чертежа и текстового документа, кончая созданием рекламных роликов и Web-страниц с применением современных компьютерных технологий.

v Лекция № 1. Введение. - Предмет инженерной графики, её задачи и место в подготовке инженеров - ЕДИНАЯ СИСТЕМА КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ (ЕСКД) - Основные требования ГОсударственных СТандартов (ГОСТов) к графическому оформлению чертежей: • форматы чертежей • масштабы изображений • типы и толщина линий на чертежах • нанесение надписей на чертежах • основные правила нанесения размеров на чертежах

Учебный курс «Инженерная графика (ИГ)» - первая общетехническая дисциплина, в которой даются знания, необходимые студенту для изучения последующих общеинженерных и технических дисциплин. Её классической теоретической основой служат начертательная геометрия и стандарты технического черчения, а областью практического применения - инженерное дело. Цель курса ИГ - дать студентам знания, приобрести умения и навыки, которые понадобятся будущему инженеру для изложения технических замыслов и идей для последующего их воплощения на практике. Предметом ИГ является составление и чтение чертежей и геометрических моделей трёхмерных фигур, образующих техническое изделие.

Задачи «Инженерной графики» : 1) ознакомление с теоретическими основами построения изображений точек, прямых, плоскостей и классических видов линий и поверхностей; 2) ознакомление с решениями задач на взаимную принадлежность и взаимное пересечение геометрических фигур; 3) определение натуральных величин отрезков и углов, построение развёрток и сечений простейших поверхностей трёхмерных тел; 4) изучение способов построения изображения простых предметов в ортогональных и аксонометрических проекциях по стандартам норм и правил ЕСКД; 5) умение определять геометрические формы простых технических деталей по чертежу; 6) ознакомление с изображением соединения деталей (сборочный чертёж).

Оформление чертежей В СССР в середине 60 -х годов ХХ века большим авторским коллективом был разработан основной комплекс стандартов - - Единая система конструкторской документации (ЕСКД). Этот комплекс, включающий в себя более ста ГОСТов, вводит единые правила оформления конструкторской документации и устанавливает единую терминологию, используемую при проектировании как в машиностроении, так и в строительстве. В ЕСКД чётко определяются такие понятия, как деталь, сборочная единица, изделие, комплект и т. д. В ЕСКД все стандарты имеют определённую структуру обозначений и названий. Например, ГОСТ 2. 304 -81 «Шрифты чертёжные» означает, что стандарт входит в комплекс ЕСКД (первая цифра - 2), номер стандарта - 304, год регистрации -1981, название - «Шрифты чертёжные» . Рассмотрим требования, предъявляемые к оформлению чертежей, основополагающих ГОСТов, каковыми являются: «Форматы» , «Масштабы» , «Линии» , «Шрифты» , «Нанесение размеров»

ГОСТ 2. 301 -68 «Форматы» Чертеж должен выполняться на листе бумаги стандартного формата. Стандартом установлены пять основных форматов чертежей, которые обозначаются: А 0, А 1, А 2, А 3, и А 4. За основной формат, обозначаемый А 0, принимают лист прямоугольной формы, площадь которого равна одному квадратному метру. Последующие основные форматы образуются посредством деления длинной стороны прямоугольного формата пополам. Габариты листов: А 0 1189 х841 А 3 297 х420 А 1 594 х841 А 4 297 х210 А 2 594 х420 А 5 148 х210 Рис. 1. 1 Образование основных стандартных форматов чертежа

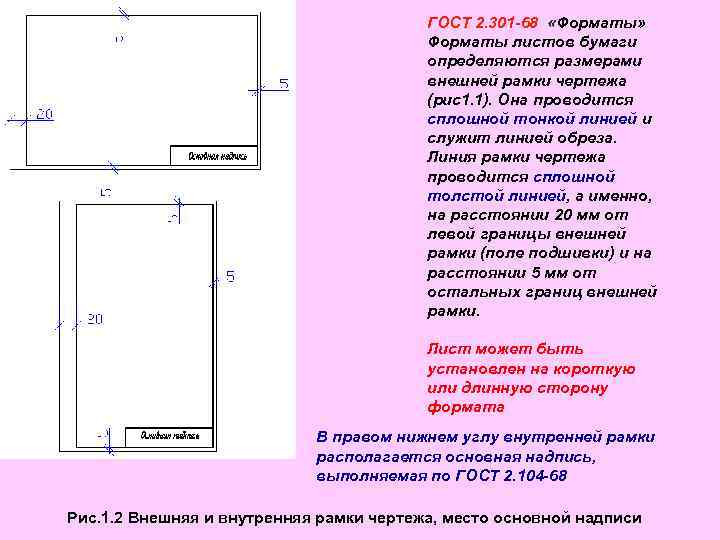ГОСТ 2. 301 -68 «Форматы» Форматы листов бумаги определяются размерами внешней рамки чертежа (рис1. 1). Она проводится сплошной тонкой линией и служит линией обреза. Линия рамки чертежа проводится сплошной толстой линией, а именно, на расстоянии 20 мм от левой границы внешней рамки (поле подшивки) и на расстоянии 5 мм от остальных границ внешней рамки. Лист может быть установлен на короткую или длинную сторону формата В правом нижнем углу внутренней рамки располагается основная надпись, выполняемая по ГОСТ 2. 104 -68 Рис. 1. 2 Внешняя и внутренняя рамки чертежа, место основной надписи

ГОСТ 2. 302 -68 «Масштабы» Изображение предмета на чертеже может быть выполнено в натуральную величину, уменьшенным и увеличенным. Масштаб - это отношение линейных размеров изображённого на чертеже предмета к его истинным размерам. ГОСТ 2. 302 -68 устанавливает следующие масштабы: Масштабы уменьшения - 1: 2; 1: 2. 5; 1: 4; 1: 5; 1: 10; 1: 15; 1: 20; 1: 25; 1: 40; 1: 75; 1: 100; 1: 200; Масштабы увеличения - 2: 1; 2. 5: 1; 4: 1; 5: 1; 10: 1; 40: 1; 50: 1; 100: 1; Натуральная величина - 1: 1 Изображение предмета на чертеже в масштабе вызвано только необходимостью правильного зрительного восприятия формы изображаемого предмета. Поэтому, независимо от масштаба, размеры предмета на чертеже проставляются истинные.

ГОСТ 2. 303 -68 «Линии» устанавливает тип и толщину линий, применяемых на чертеже. Типы линий: сплошная основная, сплошная тонкая, сплошная волнистая, штриховая, штрихпунктирная тонкая, штрихпунктирная утолщённая, разомкнутая и сплошная тонкая с изломами. Толщины всех типов линий зависят от принятой на чертеже толщины линии видимого контура, обозначаемой латинской буквой S (от 0. 6 мм до 1. 5 мм). Выбранные толщины линий должны быть одинаковыми для всех изображений на данном чертеже, выполненных в одном масштабе. В штриховых линиях штрихи должны быть равной длины (2… 8 мм), а промежутки между ними одинаковыми (1… 2 мм). В штрихпунктирных линиях штрихи должны быть равной длины (5… 30 мм), а промежутки (между которыми ставится точка или штрих длиной 1 мм) одинаковыми (3… 5 мм). Штрихпунктирные линии должны пересекаться и заканчиваться штрихами. Центровые линии должны выходить за очертания окружности на 3 - 5 мм. Для окружностей, диаметр которых 12 мм и менее, центровые линии вычерчивают сплошными тонкими.

ГОСТ 2. 304 -81 «Шрифты чертежные» устанавливает следующие размеры шрифта: 1. 8; 2. 5; 3. 5; 5; 7; 10; 14; 20; 28; 40. Размер шрифта H определяет высоту прописных (заглавных) букв и цифр в миллиметрах. Стандарт устанавливает два типа шрифта в зависимости от толщины d линий шрифта: тип А (d=H/14, Н=14 d) без наклона и с наклоном 75° к горизонтальной строке; тип Б (d=H/10, Н=10 d) без наклона и с наклоном 75° к горизонтальной строке. Эти шрифты включают русский, латинский и греческий алфавиты, а также арабские и римские цифры. Все надписи и размерные числа на чертежах должны быть чёткими и ясными. Поэтому разработан стандарт и простая конструкция начертания литер. Построение шрифтов выполнено на сетке ( «миллиметровке» ). Это удобно и позволяет изучить форму и конструкцию букв и цифр, соотношение отдельных элементов. Здесь: Н=№ шрифта - высота цифр и заглавных букв, h - высота строчных букв (ширина средней дорожки).

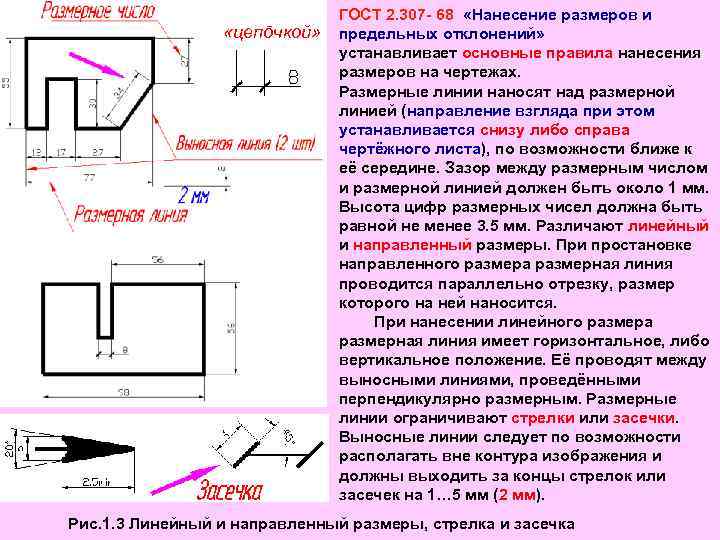ГОСТ 2. 307 - 68 «Нанесение размеров и «цепōчкой» предельных отклонений» устанавливает основные правила нанесения размеров на чертежах. Размерные линии наносят над размерной линией (направление взгляда при этом устанавливается снизу либо справа чертёжного листа), по возможности ближе к её середине. Зазор между размерным числом и размерной линией должен быть около 1 мм. Высота цифр размерных чисел должна быть равной не менее 3. 5 мм. Различают линейный и направленный размеры. При простановке направленного размера размерная линия проводится параллельно отрезку, размер которого на ней наносится. При нанесении линейного размера размерная линия имеет горизонтальное, либо вертикальное положение. Её проводят между выносными линиями, проведёнными перпендикулярно размерным. Размерные линии ограничивают стрелки или засечки. Выносные линии следует по возможности располагать вне контура изображения и должны выходить за концы стрелок или засечек на 1… 5 мм (2 мм). Рис. 1. 3 Линейный и направленный размеры, стрелка и засечка

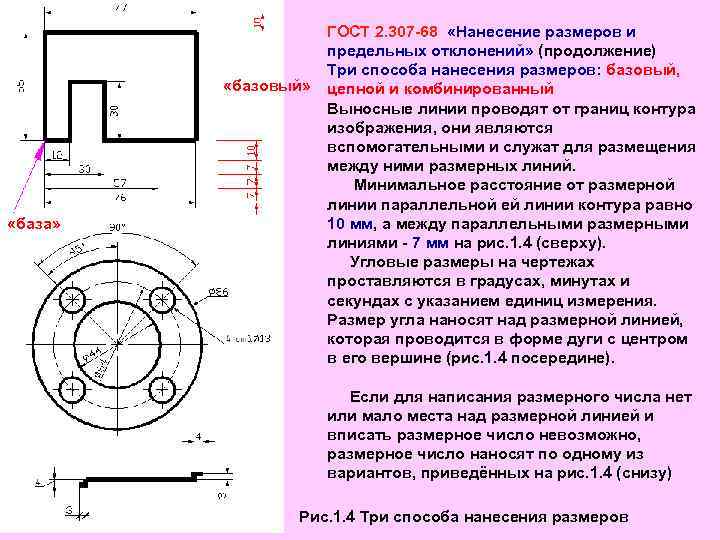ГОСТ 2. 307 -68 «Нанесение размеров и предельных отклонений» (продолжение) Три способа нанесения размеров: базовый, «базовый» цепной и комбинированный Выносные линии проводят от границ контура изображения, они являются вспомогательными и служат для размещения между ними размерных линий. Минимальное расстояние от размерной линии параллельной ей линии контура равно «база» 10 мм, а между параллельными размерными линиями - 7 мм на рис. 1. 4 (сверху). Угловые размеры на чертежах проставляются в градусах, минутах и секундах с указанием единиц измерения. Размер угла наносят над размерной линией, которая проводится в форме дуги с центром в его вершине (рис. 1. 4 посередине). Если для написания размерного числа нет или мало места над размерной линией и вписать размерное число невозможно, размерное число наносят по одному из вариантов, приведённых на рис. 1. 4 (снизу) Рис. 1. 5 Рис. 1. 4 Три способа нанесения размеров

ГОСТ 2. 307 -68 «Нанесение размеров и предельных отклонений» (продолжение) предусматривает применение условных обозначений в виде букв латинского алфавита и графических знаков, которые ставятся перед размерными числами. Знак « » - наносится перед размерным числом диаметра. Перед размерным числом радиуса дуги окружности всегда ставится знак в виде заглавной латинской буквы R. Радиусами рекомендуется обозначать дуги до 180°; дуги, превышающие угол 180°, обозначаются диаметром. Для простановки размеров квадрата применяют знак « » , высота которого равна 7/10 высоты размерного числа. Следует отметить, что знак «квадрата» наносят только на том изображении, на котором он проецируется в линию. Знак уклона «<» прямой указывают на полке линии-выноски. Уклон i представляет собой тангенс угла между данной прямой (гипотенузой) и её катетом. Знак уклона располагается так, чтобы острый угол его был направлен в сторону уклона прямой. Уклон на Рис. 1. 5 Условные обозначения чертеже задают простой дробью, в процентах стандарта ГОСТ 2. 307 -68 или в промилях (от лат. «промилле» - тысячная часть числа).

ГОСТ 2. 307 -68 «Нанесение размеров и предельных отклонений» (продолжение) предусматривает применение условных обозначений в виде букв латинского алфавита и графических знаков, которые ставятся перед размерными числами. Конусность указывают в виде простого дробного числа (рис. 1. 6 сверху). Величину конусности определяют отношением разности диаметров двух поперечных сечений конуса к расстоянию между этими сечениями. А именно: K = (D - d)/H; Простые плоские детали изображаются в виде одной проекции. Толщину детали обозначают строчной буквой S и за ней указывается значение толщины в мм. Длину предмета указывают буквой L. Фаски на чертежах наносят: двумя линейными размерами или одним линейным и одним угловым. Если угол фаски равен 45°, применяют Рис. 1. 6 Конусность, фаска, упрощенное обозначение фаски, когда размерная толщина, длина, ГОСТ 2. 307 -68 линия проводится параллельно оси конуса, а надпись выполняется по типу: « 2 х45°» (рис. 1. 6 снизу). Фаска - результат скашивания(обрезания) кромки детали плоскостью или поверхностью усечённого конуса

1. В центре листа выполняется центрированная надпись названия работы шрифтом № 10. Под названием тем же шрифтом - код чертежа: ЧГ - аббревиатура слов «черчение геометрическое» ; 01 - номер графической работы; 13 - номер варианта (следует писать свой номер - порядковый номер студента в журнале успеваемости); 13 -3 - шифр кафедры, ведущей обучение студента) 2. Сверху и снизу на расстоянии 5 мм от внутренней рамки выполняются надписи названий министерства (предприятия) и города, в котором расположено ВУЗ шрифтом № 7 3. В центре поля, расположенного между кодом чертежа «ЧГ. __. 13 -3» и городом- годом выполняется надпись Фамилия И. О. , выравниваемая по правому краю, шрифтом № 5 4. Надписи «Выполнил: ст. гр. 3 ЭН-101» и «Проверил: Артюхин Г. А. » выполняются шрифтом № 5 5. Надпись наименования обучающей кафедры, выравниваемая по правому краю, шрифтом № 3. 5 6. Центрированная надпись наименования ВУЗа выполняется шрифтом № 5 Рис. 1. 7 Образец оформления титульного листа графической работы № 1

Данные для оформления листов № 2, № 3 и № 4 графической Надпись(код чертежа) для хранения в архиве «Черчение работы геометрическое» . Состав работы: 4 листа А 4: лист № 1: «Титульный» ; лист № 2: «Деталь техническая» ; лист № 3: «Эллипс» : 2 способа построения ; лист № 4: «Многоугольник» : построение описанного и вписанного многоугольников. Срок выполнения: 4 недели Рис. 1. 8 Образец оформления основной надписи по ГОСТу 2. 104 -68

Рис. 1. 8 Заполнение основной надписи по ГОСТу 2. 104 -68 В ВУЗах заполняют только графы, обозначенными числами в скобках: 1 – Обозначение (код) чертежа. 2 – Наименование изделия. 3 – Масштаб. 4 - Фамилия ИО студента. 5 – Подпись студента. 6 - Дата. 7 – Фамилия преподавателя. 8 – Подпись педагога. 9 – Дата. 10 – Обозначение материала детали. 11 – Номер листа. 12 – Общее количество листов. 13 – ВУЗ. Факультет. № учебной группы. 14 – Стадия разработки чертежа (У – учебный процесс, «Р» - рабочий чертёж).

Последовательность работы над листом № 2: 1. Построить внутреннюю рамку чертежа и основную надпись по форме № 2 ГОСТ 2. 104 -68 (рис. 1. 8) ВНИМАНИЕ! 10 тонких линий, остальные основной толщины. 2. По первой букве своей фамилии выбрать вариант задания и в нём вычислить значение линейного размера, связанного с латинской буквой N. Например, студент Усманов И. И. выбирает в задании «У» расстояние N +80=82, т. к. его порядковый номер в списке успеваемости равен N = 2. 3. Построить две проекции детали, нанести размеры, уделить внимание на толщину и типы линий 4. Рабочие линии, выполняемые «паутинкой» для построения сопряжений, не стирать. Рис. 1. 9 Образец оформления листа № 2 «Деталь техническая»

Контрольные вопросы: 1. Сколько листов А 4 включает в 1. 16 листов себя формат А 0? 2. Что обозначено в верхней 2. Уклон: 1: 8; 8 строке? процентов; 80 промилле 3. Чему равна толщина детали S 2? 3. Толщина S=2 мм 4. Чему равна длина детали L 125? 4. Длина L=125 мм Лекция закончена !!! УРА!!!

v Лекция № 2. Некоторые геометрические построения - Деление отрезка прямой - Построение параллельной прямой - построение перпендикуляра к прямой - Деление окружности на равные части - Сопряжение двух окружностей дугой третьей окружности - Сопряжение окружности и прямой - Скругление углов (сопряжение двух прямых) - Циркульные кривые (овалы): • построение эллипса - Лекальные кривые: • построение эллипса

СМЕШАННОЕ (±) ВНУТРЕНЕЕ Алгоритм: (-) 1) Вычисление радиусов дуг центра сопряжения Ос и построение его: R 1*=Rc ± R 1; R 2*=Rc ± R 2; Из центров О 1 и О 2 проводим дуги окружностей, радиусы которых равны R 1* и R 2* соответственно. Точка пересечение дуг - центр сопряжения Ос. ВНЕШНЕЕ 2) Определение точек (+) касания - точки пересечения лучей Ос-О 1 и Ос-О 2 с окружностями О 1 и О 2 3) Построение дуги сопряжения Рис. 2. 1 Типы сопряжений: внутреннее, внешнее и смешанное

Дано: две окружности с центрами О 1 и О 2 и радиусами R 1 и R 2 соответственно. ***************** Построить внутреннее сопряжение радиуса RC

Алгоритм: 1) Вычисляем радиусы дуг центра сопряжения и строим этот центр Ос, а именно: R 1*=Rc - R 1 =70 - 30 = 40; R 2*=Rc - R 2 =70 - 20 = 50; Из центров О 1 и О 2 проводим дуги, радиусы которых равны R 1*=40 и R 2*=50 соответственно. Точка пересечение дуг и есть центр сопряжения Ос.

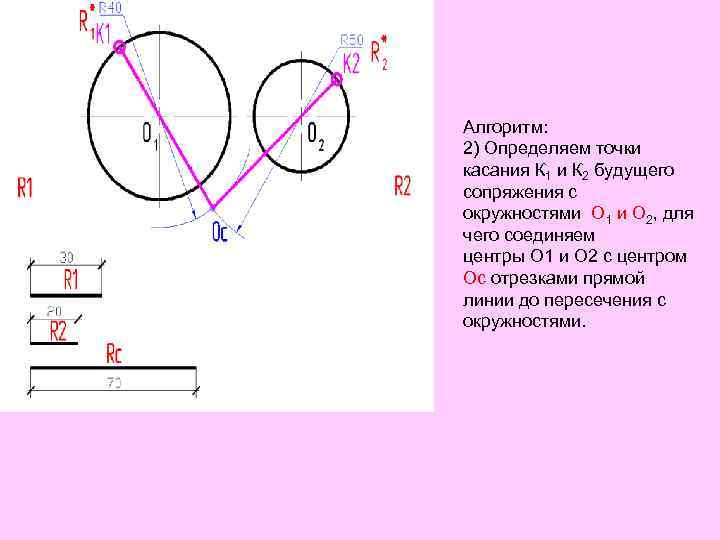Алгоритм: 2) Определяем точки касания К 1 и К 2 будущего сопряжения с окружностями О 1 и О 2, для чего соединяем центры О 1 и О 2 с центром Ос отрезками прямой линии до пересечения с окружностями.

Алгоритм: 3) Соединяем точки касания К 1 и К 2 дугой окружности радиуса Rc из центра Ос. Внутреннее сопряжение построено !

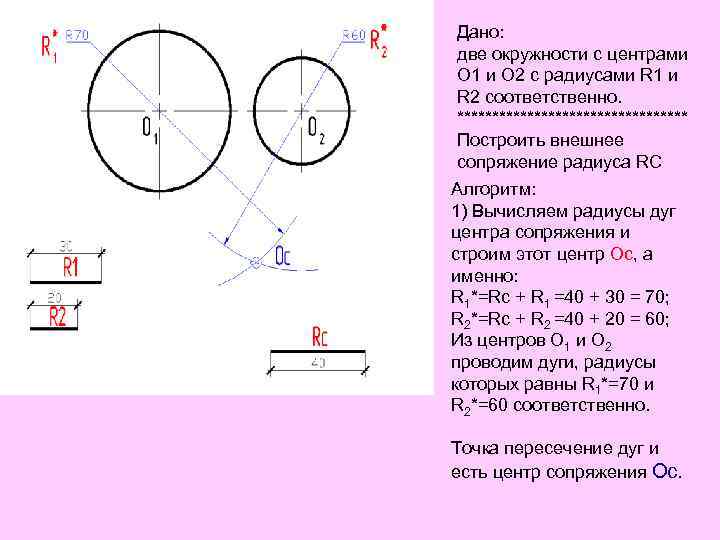Дано: две окружности с центрами О 1 и О 2 с радиусами R 1 и R 2 соответственно. ***************** Построить внешнее сопряжение радиуса RC Алгоритм: 1) Вычисляем радиусы дуг центра сопряжения и строим этот центр Ос, а именно: R 1*=Rc + R 1 =40 + 30 = 70; R 2*=Rc + R 2 =40 + 20 = 60; Из центров О 1 и О 2 проводим дуги, радиусы которых равны R 1*=70 и R 2*=60 соответственно. Точка пересечение дуг и есть центр сопряжения Ос.

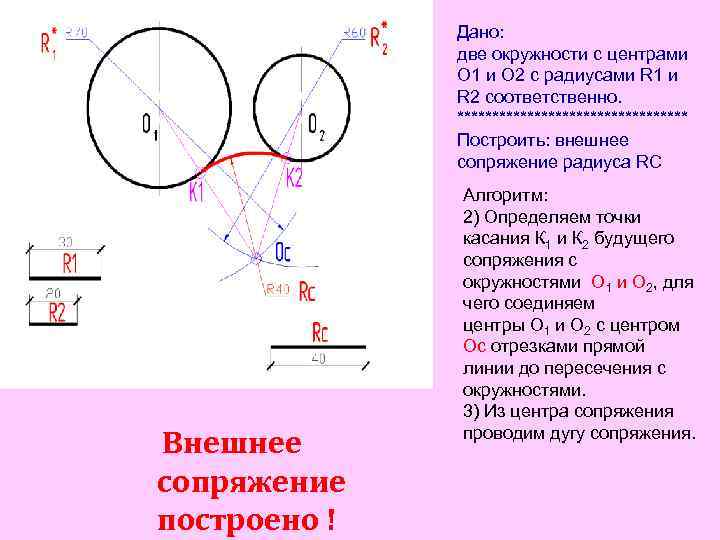Дано: две окружности с центрами О 1 и О 2 с радиусами R 1 и R 2 соответственно. ***************** Построить: внешнее сопряжение радиуса RC Алгоритм: 2) Определяем точки касания К 1 и К 2 будущего сопряжения с окружностями О 1 и О 2, для чего соединяем центры О 1 и О 2 с центром Ос отрезками прямой линии до пересечения с окружностями. 3) Из центра сопряжения проводим дугу сопряжения. Внешнее сопряжение построено !

Сопряжение окружности и прямой

1) Вычисление радиуса дуги центра сопряжения Ос и построение его: R*=Rc ± R; Построение эквидистантной прямой Из центра О проводим дугу окружности, радиус которой равен R* Точка пересечение дуги и эквидистанты - центр сопряжения Ос. 2) Определение точек касания К 1 и К 2 с окружностью О 1 и прямой 3) Построение дуги сопряжения Rс

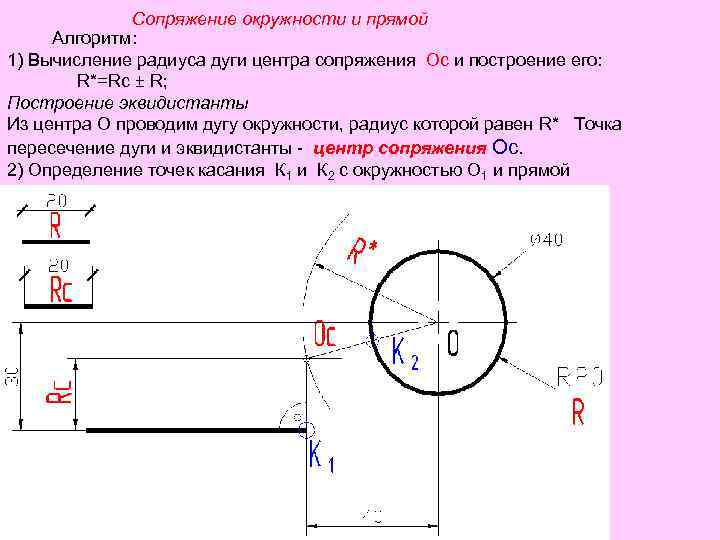Сопряжение окружности и прямой Алгоритм: 1) Вычисление радиуса дуги центра сопряжения Ос и построение его: R*=Rc ± R; Построение эквидистанты Из центра О проводим дугу окружности, радиус которой равен R* Точка пересечение дуги и эквидистанты - центр сопряжения Ос. 2) Определение точек касания К 1 и К 2 с окружностью О 1 и прямой

Алгоритм: 1) Вычисление радиуса дуги центра сопряжения Ос и построение его: R*=Rc ± R; Построение эквидистантной прямой Из центра О проводим дугу окружности, радиус которой равен R* Точка пересечение дуги и эквидистанты - центр сопряжения Ос. 2) Определение точек касания К 1 и К 2 с окружностью О 1 и прямой 3) Построение дуги сопряжения Rс

Скругление угла Алгоритм: 1) Построение эквидистантных прямых, пересечение которых - центр сопряжения Ос. 2) Определение точек касания - точки пересечения лучей К 1 и К 2 с окружностью О 1 и прямой 3) Построение дуги сопряжения Rс

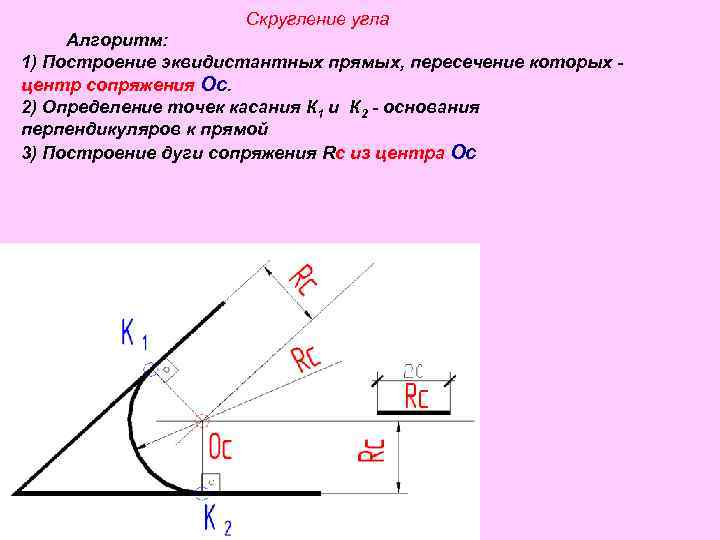Скругление угла Алгоритм: 1) Построение эквидистантных прямых, пересечение которых - центр сопряжения Ос. 2) Определение точек касания К 1 и К 2 - основания перпендикуляров к прямой 3) Построение дуги сопряжения Rс из центра Ос

Построить: эллипс размером 80 х50 как циркульную кривую (овал) Определяем и обозначаем квадранты эллипса : две точки на малой оси и две на большой

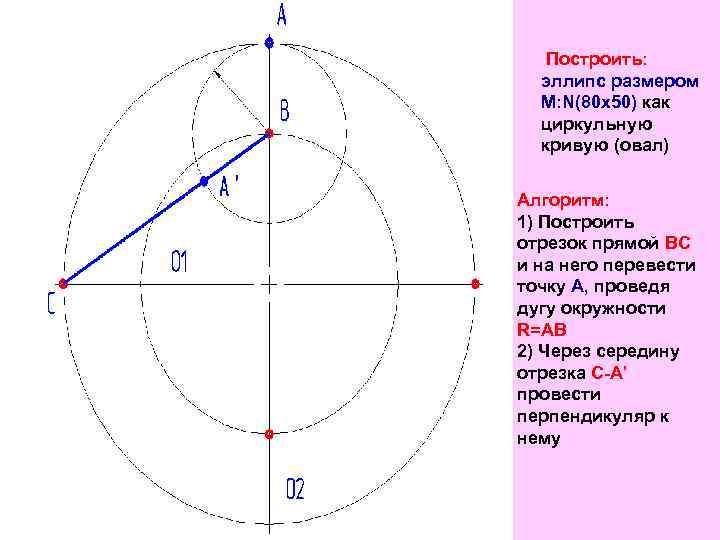Построить: эллипс размером M: N(80 х50) как циркульную кривую (овал) Алгоритм: 1) Построить отрезок прямой ВС и на него перевести точку А, проведя дугу окружности R=AB 2) Через середину отрезка С-А’ провести перпендикуляр к нему

Построить: эллипс размером M: N(80 х50) как циркульную кривую (овал) Алгоритм: 1) Построить отрезок прямой ВС и на него перевести точку А, построив дугу окружности радиусом R=AB 2) Через середину отрезка С-А’ провести перпендикуляр к нему, пересечение которого с большой и малой осями эллипса, приведёт к образованию двух центров сопряжения О 1 и О 2

Алгоритм: … …. 2) Через середину отрезка С-А’ провести перпендикуляр к нему, пересечение которого с большой и малой осями эллипса, приведёт к образованию двух центров сопряжения О 1 и О 2 3) Из центра О 2 проводим дугу окружности R=O 2 -В 4) Из О 1 дугу R=O 1 -С

Алгоритм: 4) Из О 1 дугу R=O 1 -С 5) Отразив зеркально центры сопряжений, строим овал полностью Задача решена !

Построить: эллипс размером 120 х60 как лекальную кривую Алгоритм: 1) Из центра окружностей провести несколько лучей до пересечения с большой и малой окружностями

Построить: эллипс размером 80 х50 как лекальную кривую Алгоритм: 1) Из центра окружностей провести несколько лучей до пересечения с большой и малой окружностями 2) Из точек пересечения луча с окружностями провести горизонтальную и вертикальную прямые, пересечение которых - искомая точка эллипса

Алгоритм: 3) Соединение Задача решена ! построенных в пункте № 2 точек эллипса выполняется посредством построения сплайна Для вычерчивания лекальной кривой лекало подбирают так, чтобы его кромка совпадала не менее чем с четырьмя точками кривой. При этом соединяют линией только две из них и далее лекало передвигают к последующим точкам

Дано: окружность произвольного радиуса *************** Построить: вписанный правильный пятиугоугольник Алгоритм: 1) Определим середину горизонтального радиуса окружности - точку S

Дано: окружность произвольного радиуса *************** Построить: вписанный правильный многоугольник Алгоритм: 1) Определим середину горизонтального радиуса окружности - точку S 2) Построим две окружности: одну из центра S радиусом, равным половине радиуса исходной окружности, другую - из точки С радиусом R=BC

Алгоритм: 1) Определим середину горизонтального радиуса окружности - точку S 2) Построим две окружности: одну из центра S радиусом, равным половине радиуса исходной окружности, другую - из точки С радиусом R=BC 3) Отрезок 1 -2 есть искомая сторона пятиугольника

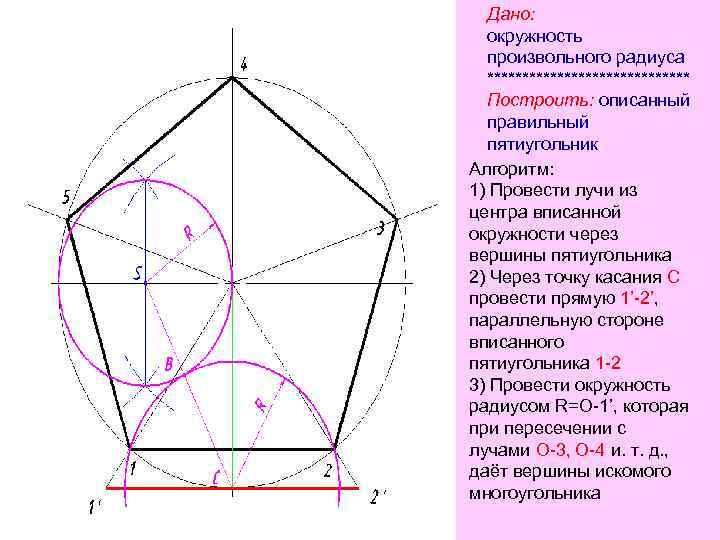Дано: окружность произвольного радиуса *************** Построить: описанный правильный пятиугольник Алгоритм: 1) Провести лучи из центра вписанной окружности через вершины пятиугольника 2) Через точку касания С провести прямую 1’-2’, параллельную стороне вписанного пятиугольника 1 -2 3) Провести окружность радиусом R=O-1’, которая при пересечении с лучами О-3, О-4 и. т. д. , даёт вершины искомого многоугольника

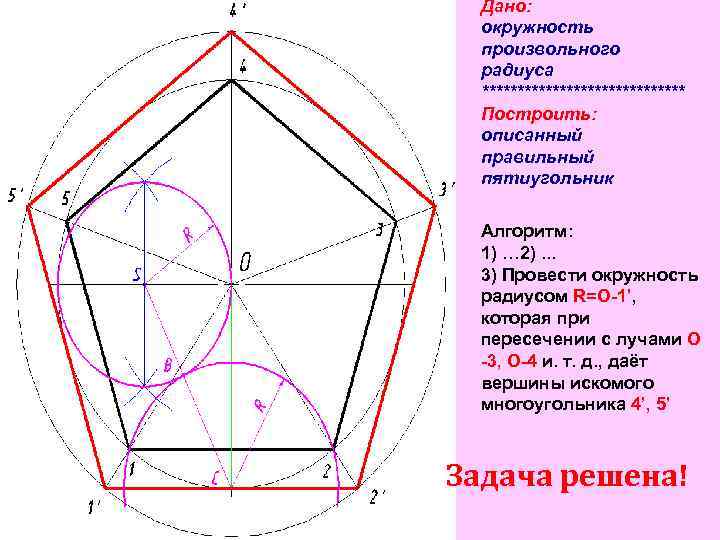Дано: окружность произвольного радиуса *************** Построить: описанный правильный пятиугольник Алгоритм: 1) … 2). . . 3) Провести окружность радиусом R=O-1’, которая при пересечении с лучами О -3, О-4 и. т. д. , даёт вершины искомого многоугольника 4’, 5’ Задача решена!

v Лекция № 3. Основы начертательной геометрии - История становления - Виды проецирования - Метод Гаспара Монжа (1746 -1818 гг). - Чертёж, изображение точки на нём.

Начертательная геометрия Аналитическая геометрия

Эпю р (с французского epure - чертёж) — чертёж, на котором пространственная фигура изображена методом нескольких (по ГОСТ трёх, но не всегда) плоскостей. Обычно оно даёт 3 вида: фронтальную, горизонтальную и профильную проекции (в строительных терминах, - фасад, план, профиль). Чертёж проецируется на взаимно перпендикулярные, а затем развернутые в одну, плоскости. Вертолёт МИ-8 в трёх проекциях, изображённый с помощью эпюра Монжа

Создание «Начертательной геометрии» , трактат которой вышел в свет только в 1799 г. под заглавием «Géométrie descriptive» , послужило началом и основой работ, позволивших новой Европе овладеть геометрическими знаниями Древней Греции; работы же по теории поверхностей, помимо своего непосредственного значения, привели к выяснению понятия непрерывности и к раскрытию смысла неопределенности, которая возникает при интегрировании уравнений с частными производными, с произвольными постоянными и тем более с появлением произвольных функций.

С изучения теоретических основ НГ как базы инженерной графики мы начинаем её освоение. π2 π3 1 π1 Рис. 3. 1 Декартовая (картезианская) система координат и плоскости проекций, применяемые в инженерной графике: пространственная 3 М (3 D) модель точки А (слева); плоская 2 М (2 D) модель (чертёж - эпюр Монжа) точки А (справа); А 1, А 2, А 3 - ортогональные проекции точки А

В инженерной деятельности реальный объект при его создании и совершенствовании заменяется моделью, - его аналогом, в котором оставлены лишь основные, с точки зрения исследователя, геометрические свойства: форма, размеры и топологические связи (графы). Такой моделью в инженерной графике является чертёж, а именно изображение проекций пространственного предмета на плоскости. Проекцией точки на плоскость называется точка пересечения проецирующего луча, проходящего через заданную в пространстве точку с плоскостью проекций. Для построения проекций используется параллельное ортогональное (прямоугольное) проецирование. В качестве плоскостей проекций служат три взаимно перпендикулярных 1 плоскости (рис. 3. 1): π1 - горизонтальная плоскость проекций; π2 - фронтальная плоскость проекций; π3 - профильная плоскость проекций. Эти плоскости взаимно пересекаются по прямым линиям - осям: X, Y, Z. Оси пересекаются в одной точке О, называемой «начало координат» . Идея Г. Монжа: Переход от 3 М модели к 2 М чертежу осуществляется посредством вращения горизонтальной и профильной плоскостей вокруг осей X и Z соответственно до совмещения их с фронтальной плоскостью проекций (рис. 3. 1).

КП -картинная плоскость Ο Ο Рис 3. 2 Параллельное Рис 3. 3 Центральное проецирование

Свойства центрального проецирования: 1. Проекция точки - точка; 2. Проекция прямой - прямая; 3. Точка, принадлежащая прямой, принадлежит проекции этой прямой. При параллельном проецировании свойства центрального сохраняются, поскольку это его частный случай, и добавляются ещё три: 4. Проекции параллельных прямых параллельны между собой; 5. Отношение отрезков двух параллельных прямых равно отношению проекций этих прямых; 6. Отношение отрезков прямой равно отношению проекций этих отрезков (теорема Фалěса). При ортогональном проецировании (лучи перпендикулярны картинной плоскости КП) как частном случае параллельного проецирования добавляется седьмое свойство: 7. Прямой угол прямоугольного треугольника проецируется на плоскость проекций без искажения , т. е. равен 900 , в случае, если один из катетов параллелен этой плоскости проекций, а второй ей не перпендикулярен (теорема о проецировании прямого угла без его искажения).

Итак, что такое чертёж, рисунок, эскиз? Рисунок (эскиз)- изображение предмета, выполненное «на глаз» с относительно выдержанными размерами и положением отдельных его элементов. Чертеж (эпюр)- изображение предмета, выполненное по особым правилам (ГОСТам) с применением чертежных инструментов в точной зависимости от размеров и положения отдельных его элементов в пространстве. К проекционным изображениям в НГ предъявляются следующие требования: 1. Обратимость - возможность восстановления оригинала по его проекционным изображениям (чертежу) и определения формы и размеров объекта, его положение и связь с окружающей средой; 2. Наглядность - чертёж должен создавать пространственное представление о форме предмета; 3. Точность; 4. Простота - изображение должно быть простым по построению.

Метод Монжа - метод ортогонального проецирования Суть метода состоит в том, что в качестве основных плоскостей проекций выбираются две взаимно перпендикулярные плоскости, и чертёж представляет собой две картины П 1(нижняя, вид сверху) и П 2(верхняя, вид спереди). Однозначность представления объекта обеспечивается моделью Рене Декарта: три взаимно перпендикулярных оси, ОZ направлена вверх, OX - влево от наблюдателя и OY направлена в наблюдателя. Любая точка, например А, задаётся тройкой чисел - абсциссой XA (левее- правее), ординатой y. A (ближе-дальше) и аппликатой ZA (выше- ниже). Термины: плоскость π1 - горизонтальная плоскость проекций (вид сверху); плоскость π2 - фронтальная плоскость проекций (вид спереди); плоскость π3 - профильная плоскость проекций (вид слева); проекция получает имя от оригинала и нижний индекс от названия плоскости проекций

Задача. Построить чертёж точки А(25, 18, 30) Алгоритм решения: 1. Измеряем расстояния от оригинала А, т. е. до его проекций: А-А 1 - высота , А-А 2 - глубина А-А 3 - ширина

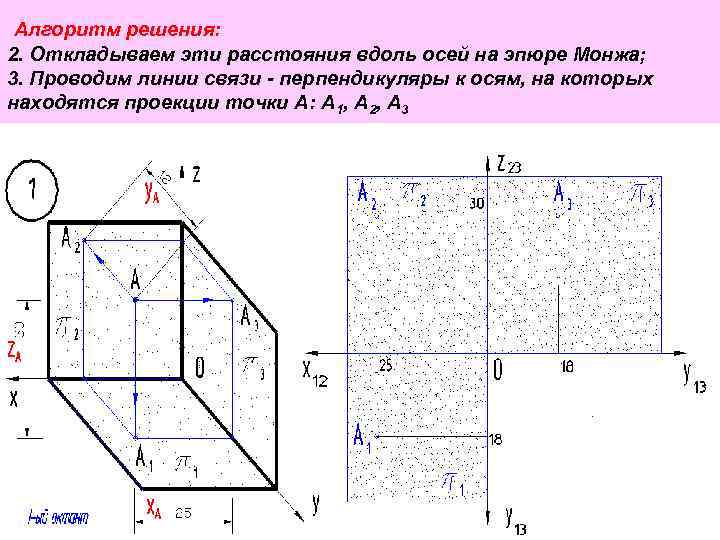Алгоритм решения: 2. Откладываем эти расстояния вдоль осей на эпюре Монжа; 3. Проводим линии связи - перпендикуляры к осям, на которых находятся проекции точки А: А 1, А 2, А 3

VIII IV V VII

А : СФЕРА(Шар) Б : Конус, Контрольные вопросы: направленный ЧТО изображено на чертежах? вершиной на зрителя В : вертикальный отрезок Лекция закончена

v Лекция № 4. - Графическое задание прямой линии (прямой). - Положение прямой относительно плоскостей проекций. - Следы прямой. Взаимное расположение точки и прямой. - Деление отрезка в данной пропорции. Длина отрезка прямой. - Взаимное положение двух прямых. Прямая в линейной алгебре, - линия 1 -го порядка, заданная общим уравнением: Ax+By+C=0; В геометрии, прямая линия - это линия, вдоль которой расстояние между двумя точками является кратчайшим. Различают 4 способа графического изображения прямой, которые связаны с исходными данными её задания. А именно, если заданы: 1. Координаты двух её точек; 2. Две проекции прямой; 3. Две пересекающиеся между собой плоскости; 4. Координаты точки и значения углов наклона прямой к плоскостям проекций.

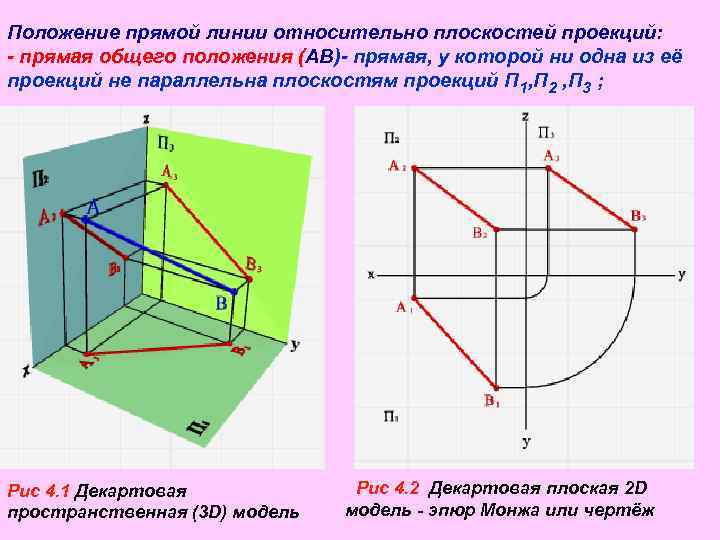Положение прямой линии относительно плоскостей проекций: - прямая общего положения (АВ)- прямая, у которой ни одна из её проекций не параллельна плоскостям проекций П 1, П 2 , П 3 ; Рис 4. 1 Декартовая Рис 4. 2 Декартовая плоская 2 D пространственная (3 D) модель - эпюр Монжа или чертёж

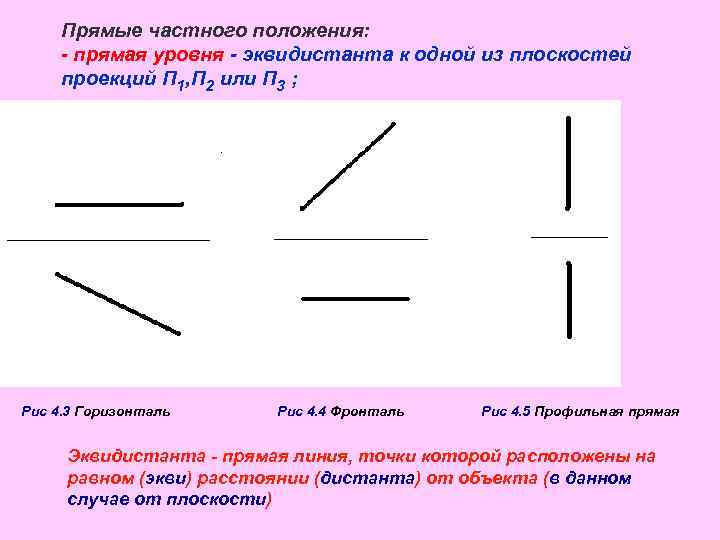Прямые частного положения: - прямая уровня - эквидистанта к одной из плоскостей проекций П 1, П 2 или П 3 ; Рис 4. 3 Горизонталь Рис 4. 4 Фронталь Рис 4. 5 Профильная прямая Эквидистанта - прямая линия, точки которой расположены на равном (экви) расстоянии (дистанта) от объекта (в данном случае от плоскости)

проецирующие прямые - прямые линии, перпендикулярные к одной из плоскостей проекций П 1, П 2 или П 3 ; Рис 4. 6 Рис 4. 7 Рис 4. 8 Горизонтально Фронтально Профильно проецирующая прямая Термин «проецирующая прямая» - то же самое, что и термины «нормаль» и «перпендикуляр»

Следы прямой линии След прямой линии - точка пересечения этой прямой с плоскостью проекций. Из-за принадлежности следа одной плоскости проекций, одна из его координат должна быть равной нулю. В зависимости от наименования плоскости, в которой расположен след, различают горизонтальный, фронтальный и профильный следы. Алгоритм: Для построения горизонтального следа М прямой необходимо: 1. продолжить её фронтальную проекцию до пересечения с осью Ох (фронтальная проекция следа М 2 построена); 2. Продолжить горизонтальную проекцию прямой до пересечения с линией связи, проходящей через М 2. Для построения фронтального следа М прямой необходимо: 1. продолжить её горизонтальную проекцию до пересечения с осью Ох (горизонтальная проекция следа М 1 построена); 2. Продолжить фронтальную проекцию прямой до пересечения с линией связи, проходящей через М 1. Линия связи - перпендикуляр к оси системы координат, на котором расположены проекции одноимённой точки.

Дано: прямая АВ *********** Построить следы прямой (бланк № 2, задача № 4)

Шаг 1. Продолжаем А 2 В 2 до Х 12 и из M 2 проводим линию связи до пересечения с продолжением проекции А 1 В 1 , - в итоге: построен горизонтальный след M 1 ***********

Шаг 2. Продолжаем горизонтальный след А 1 В 1 до Х 12 и из N 1 проводим линию связи до пересечения с А 2 В 2 , - в итоге: N 2 *********** Задача решена !

Определение длины отрезка прямой способом катетов (теорема Пифагора) Итак, требуется определить длину АВ. На рис. 4. 9 горизонтальная проекция А 1 В 1=sqrt( (x. A-x. B) 2 + +(y. A-y. B) 2 ). Искомая длина отрезка равна: АВ= sqrt( (x. A-x. B) 2 + (y. A-y. B) 2 + (z. A-z. B) 2 ); Графически длина отрезка представляет собой гипотенузу А 1 В 1* , построенную в прямоугольном треугольнике А 1 В 1 В 1* , катетами которого являются одна из проекций отрезка, например А 1 В 1 , а длина другого равна |z. A-z. B| или |y. A-y. B| , на рис. 4. 10, например, это Δz=|z. A-z. B| α -угол наклона АВ к π1 Рис. 4. 9 Рис. 4. 10

Деление отрезка прямой линии в данном соотношении (теорема Фалеса) «Если одну из сторон угла поделить на равные отрезки и через их концы провести параллельные противоположной стороне угла прямые, пересекающие другую сторону угла, то на ней образуются также равные между собой отрезки» . На рис. 4. 11 точка делит отрезок в пропорции 2: 3 Рис. 4. 11

Взаимное положение двух прямых: - параллельные прямые - прямые, лежащие в одной плоскости и не имеющие между собой общих точек; - пересекающиеся прямые - прямые, лежащие в одной плоскости и имеющие между собой одну общую точку; - скрещивающиеся прямые - прямые, которые не лежат в одной плоскости и не имеющие между собой общих точек;

параллельные прямые Задача. Через точку D провести прямую, параллельную прямой АВ. **************** Решение: 1. На основании 4 -го свойства проецирования «проекции параллельных прямых параллельны между собой» через D 1 и D 2, параллельно А 1 -В 1 и А 2 -В 2 соответственно проводим искомые проекции C 1 -D 1 и C 2 -D 2

параллельные прямые Задача решена!

Взаимное положение двух прямых: - пересекающиеся прямые Задача. Построить прямую CD, пересекающую прямую АВ в произвольной точке Т

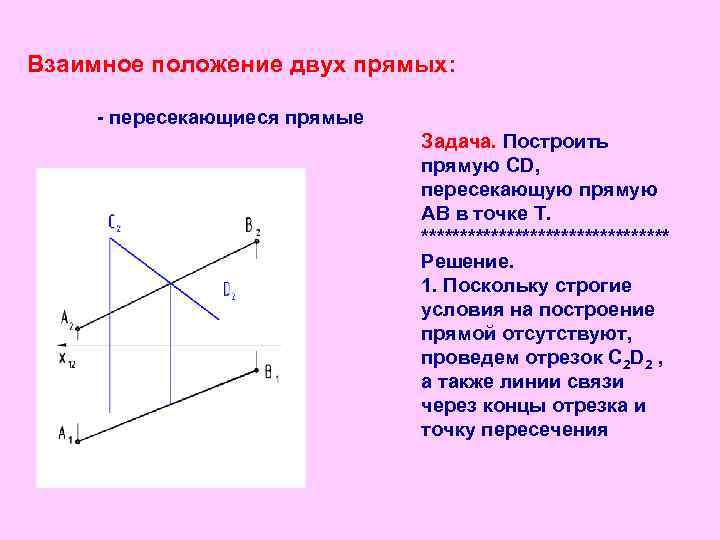Взаимное положение двух прямых: - пересекающиеся прямые Задача. Построить прямую CD, пересекающую прямую АВ в точке Т. **************** Решение. 1. Поскольку строгие условия на построение прямой отсутствуют, проведем отрезок C 2 D 2 , а также линии связи через концы отрезка и точку пересечения

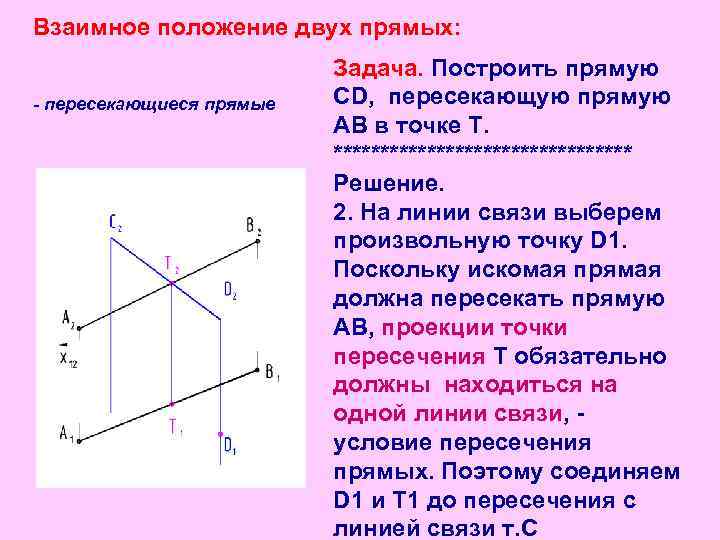Взаимное положение двух прямых: Задача. Построить прямую - пересекающиеся прямые CD, пересекающую прямую АВ в точке Т. **************** Решение. 2. На линии связи выберем произвольную точку D 1. Поскольку искомая прямая должна пересекать прямую АВ, проекции точки пересечения Т обязательно должны находиться на одной линии связи, - условие пересечения прямых. Поэтому соединяем D 1 и Т 1 до пересечения с линией связи т. С

Взаимное положение двух прямых:

Взаимное положение двух прямых: - скрещивающиеся прямые Задача. Построить скрещивающиеся прямые CD и АВ. ****************

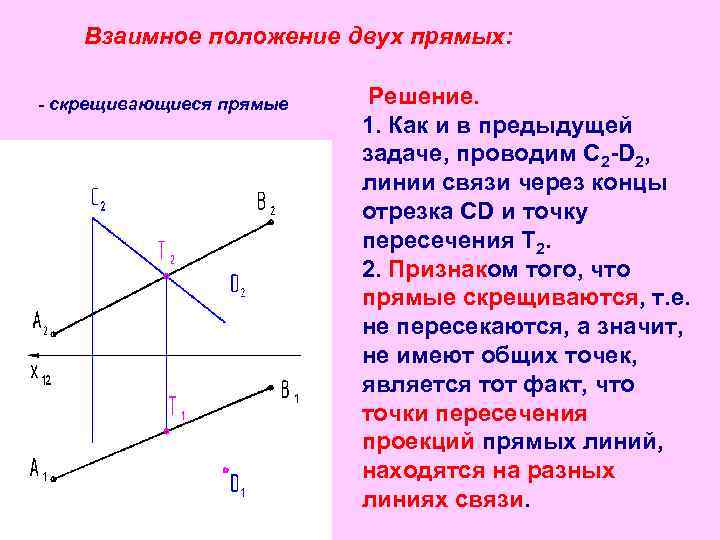Взаимное положение двух прямых: - скрещивающиеся прямые Решение. 1. Как и в предыдущей задаче, проводим С 2 -D 2, линии связи через концы отрезка CD и точку пересечения Т 2. 2. Признаком того, что прямые скрещиваются, т. е. не пересекаются, а значит, не имеют общих точек, является тот факт, что точки пересечения проекций прямых линий, находятся на разных линиях связи.

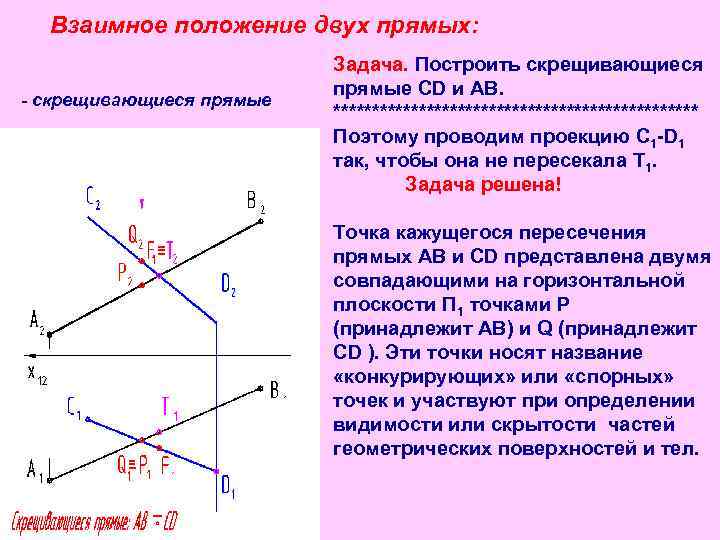Взаимное положение двух прямых: Задача. Построить скрещивающиеся прямые CD и АВ. - скрещивающиеся прямые ************************ Поэтому проводим проекцию C 1 -D 1 так, чтобы она не пересекала Т 1. Задача решена! Точка кажущегося пересечения прямых АВ и CD представлена двумя совпадающими на горизонтальной плоскости П 1 точками Р (принадлежит АВ) и Q (принадлежит CD ). Эти точки носят название «конкурирующих» или «спорных» точек и участвуют при определении видимости или скрытости частей геометрических поверхностей и тел.

На основании 7 -го свойства проецирования, а именно теоремы о проецировании прямого угла, из точки С 2 проводим перпендикуляр к А 2 В 2

Из точки О 2 проводим линию связи и на пересечении её с А 1 В 1 получаем недостающую проекцию О 1

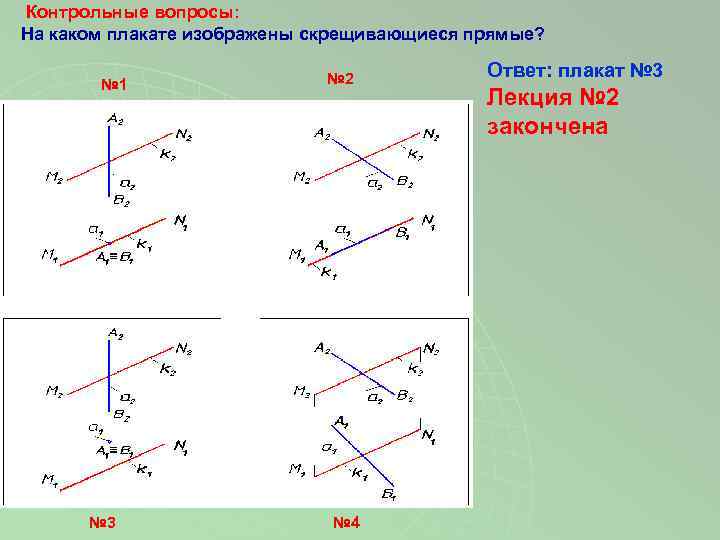Контрольные вопросы: На каком плакате изображены скрещивающиеся прямые? № 2 Ответ: плакат № 3 № 1 Лекция № 2 закончена № 3 № 4

Лекция № 5. Плоскость - Графическое задание плоскости - Положение плоскости относительно плоскостей проекций - Следы плоскости - Признаки принадлежности точки и прямой плоскости - Взаимное положение двух плоскостей Плоскость в линейной алгебре, - поверхность 1 -го порядка, задаваемая общим уравнением: Ax+By+Cz+D=0; где A, B, C, D - постоянные, не равные нулю одновременно. Различают следующие способы графического изображения плоскости (5 способов): 1. по трём точкам, не лежащим на одной прямой Σ(А, В, С); 2. двумя пересекающимися прямыми Σ(a^b); 3. двумя параллельными прямыми Ω(a//b); 4. по прямой и точке, не лежащей на этой прямой Ω(a, А); 5. следами плоскости Σ(Σ 1, Σ 2) (рис. 5. 1).

2 признака принадлежности прямой плоскости: Аксиома № 1: «Прямая принадлежит плоскости, если любые её две точки принадлежат этой плоскости» Аксиома № 2: «Прямая принадлежит плоскости, если она имеет одну общую с ней точку и параллельна какой либо прямой, расположенной в этой плоскости»

Задача. Построить недостающую проекцию ΔАВС, принадлежащего плоскости Σ, заданную пересекающимися прямыми m и n

Шаг 1. На основании аксиомы № 1, продолжим А 2 В 2 до пересечения с m 2. Получим фронтальные проекции точек 1 и 2.

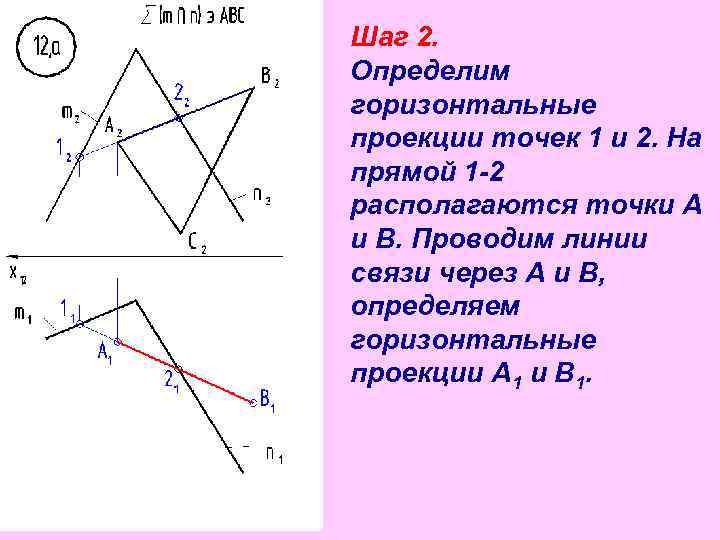Шаг 2. Определим горизонтальные проекции точек 1 и 2. На прямой 1 -2 располагаются точки А и В. Проводим линии связи через А и В, определяем горизонтальные проекции А 1 и В 1.

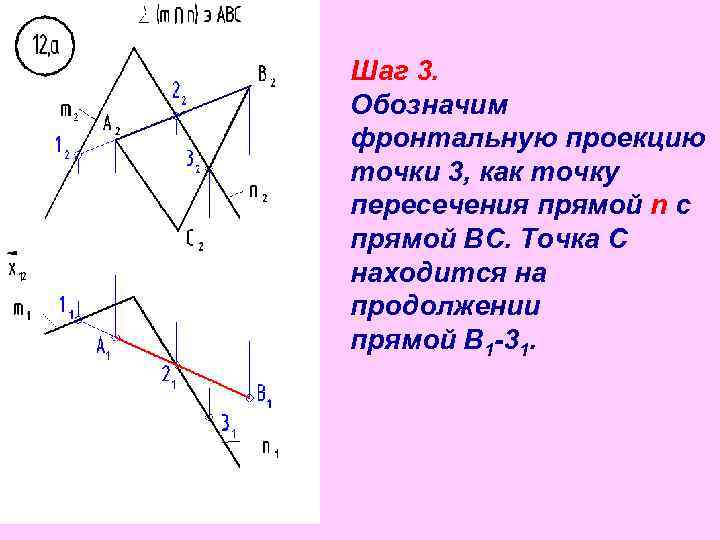Шаг 3. Обозначим фронтальную проекцию точки 3, как точку пересечения прямой n с прямой BС. Точка С находится на продолжении прямой В 1 -31.

Задача решена!

Задание плоскости тремя точками Задача. Построить главные линии плоскости - горизонталь и фронталь, пересекающиеся в точке К, принадлежащей плоскости Σ, заданной тремя точками А, В и С.

Шаг 1. Параллельно Х 12 провести горизонталь h 2, обозначить точки пересечения с АВ и ВС.