Stochastic models of aging and mortality And one

Stochastic models of aging and mortality And one man in his time plays many parts, For his shrunk shank; and his big manly voice, Turning again toward childish treble, pipes His acts being seven ages… And whistles in his sound. Last scene of all, …The sixth age shifts That ends this strange eventful history, Into the lean and slipper'd pantaloon, Is second childishness and mere oblivion, With spectacles on nose and pouch on side, His youthful hose, well saved, a world too wide Sans teeth, sans eyes, sans taste, san everything. A nonstochastic model of aging and mortality by W. Shakespeare and Titian

What is aging? • J. M. Smith (1962): Aging processes are “those which render individuals more susceptible as they grow older to the various factors, intrinsic or extrinsic, which may cause death. ” • P. T. Costa and R. R. Mc. Crae (1995): “What happens to an organism over time. ”

• “Force of mortality” (hazard rate) increases with age

Increasing mortality as a proxy for aging • We can’t measure aging processes directly, particularly since we can’t define them. • Mortality rates are easy to measure. In most metazoans, mortality rates increase with age.

Increasing mortality as a proxy for aging • We can’t measure aging processes directly, particularly since we can’t define them. • Mortality rates are easy to measure. In most metazoans, mortality rates increase with age. • This includes us.

This is not a trivial observation! • Implicit in Roman annuity rates. • 17 th C. annuity and life-insurance rates were generally age-independent. • Annuity as gamble: Who is the best bet? • Very old (for whom the increased hazard would be most clear) rare, uncertain age. • Extreme haphazardness of plagues, wars.

Some questions about aging: 1. Why do creatures age?

Some questions about aging: 1. Why do creatures age? Old (and recurrent) idea: Improper nutrition. • “Unto the woman he said, I will greatly multiply thy sorrow and thy conception; in sorrow thou shalt bring forth children; and thy desire shall be to thy husband… In the sweat of thy face shalt thou eat bread, till thou return unto the ground; for out of it wast thou taken: for dust thou art, and unto dust shalt thou return. ”

Some questions about aging: 1. Why do creatures age? THINGS FALL APART

Some questions about aging: 1. Why do creatures age? Problems with this naïve answer • Repair. • Not universal.

Aging not universal. • Negligible senescence: prokaryotes, bristlecone pine, tortoises, lobster • Gradual senescence: mammals, birds, fish, yeast • Rapid senescence: flies, bees (workers), nematodes

Some questions about aging: 1. Why do creatures age? 2. Why does aging have the particular agepatterns that it does?

Some questions about aging: 1. Why do creatures age? 2. Why does aging have the particular agepatterns that it does? 3. Why do different species have characteristic patterns of aging?

Some questions about aging: 1. Why do creatures age? 2. Why does aging have the particular agepatterns that it does? 3. Why do different species have characteristic patterns of aging? 4. Why is aging so variable?

Some questions about aging: 1. Why do creatures age? 2. Why does aging have the particular agepatterns that it does? 3. Why do different species have characteristic patterns of aging? 4. Why is aging so variable? 5. Why is aging so constant?

The Gompertz-Makeham mortality law • Gompertz (1825): “we observe that in those tables the numbers of living in each yearly increase of age are from 25 to 45 nearly, in geometrical progression. ” • Makeham (1867): “Theory of partial forces of mortality”. Diseases of lungs, heart, kidneys, stomach, liver, brain associated with “diminution of the vital power”.

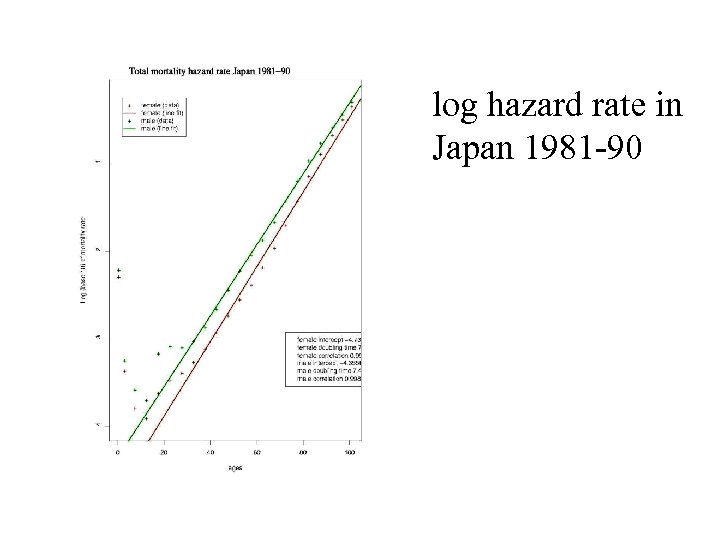log hazard rate in Japan 1981 -90

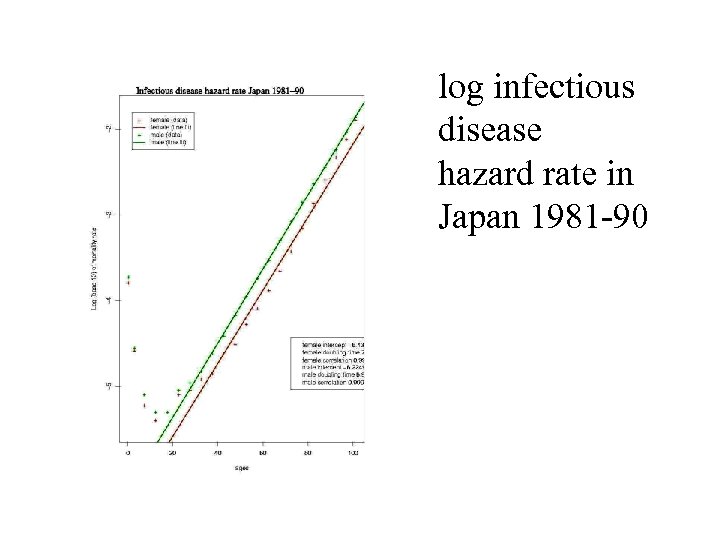log infectious disease hazard rate in Japan 1981 -90

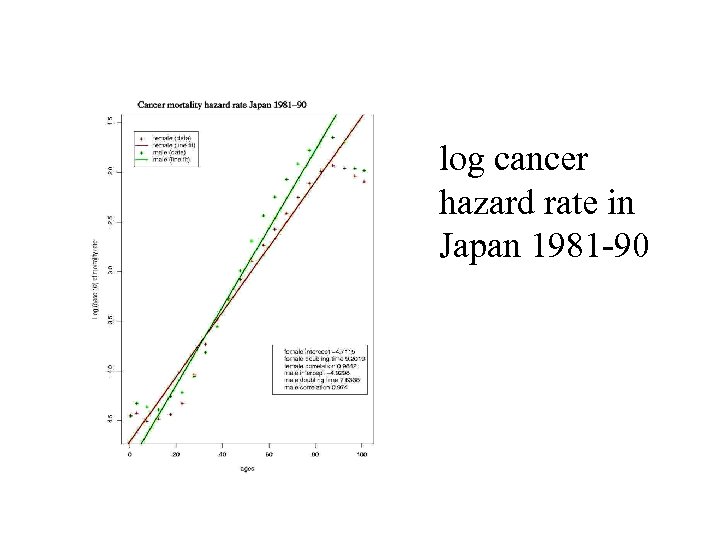log cancer hazard rate in Japan 1981 -90

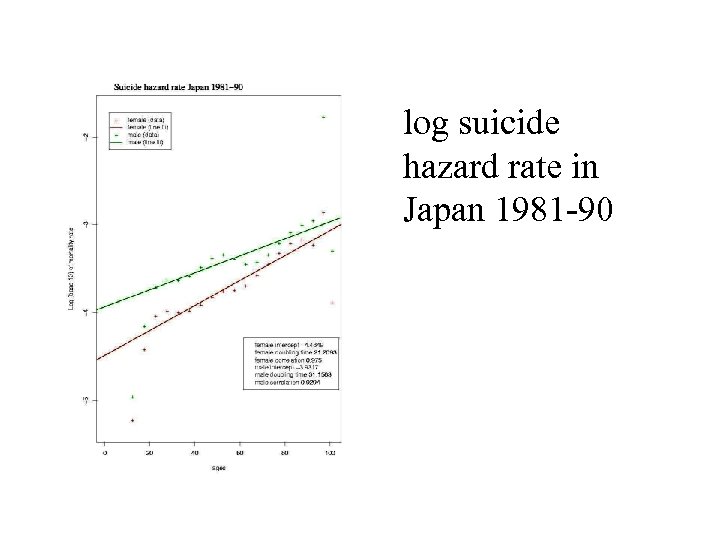log suicide hazard rate in Japan 1981 -90

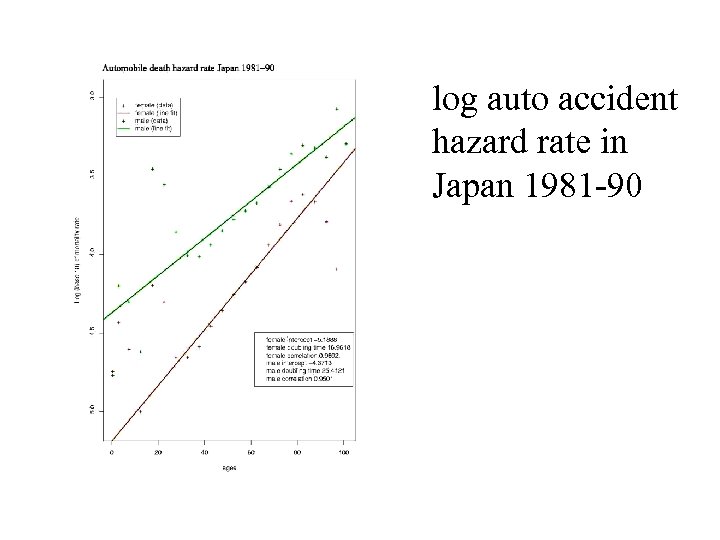log auto accident hazard rate in Japan 1981 -90

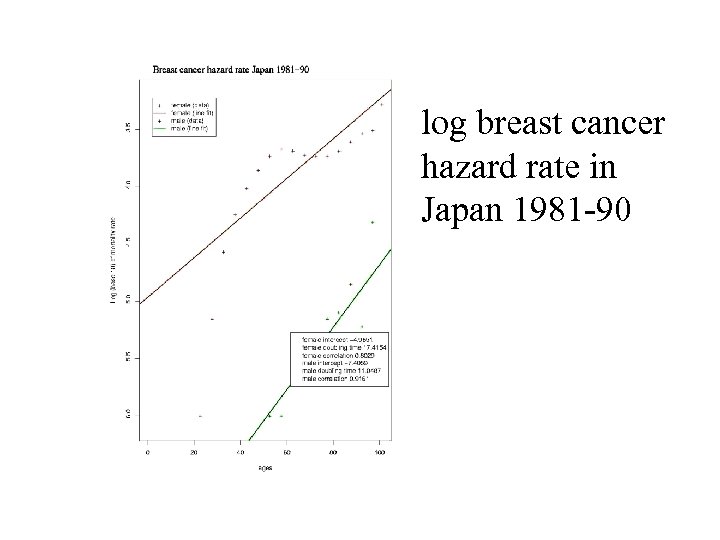log breast cancer hazard rate in Japan 1981 -90

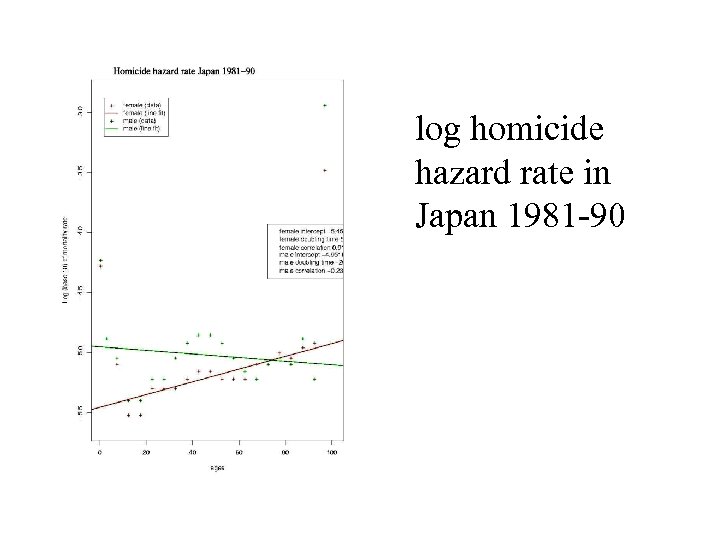log homicide hazard rate in Japan 1981 -90

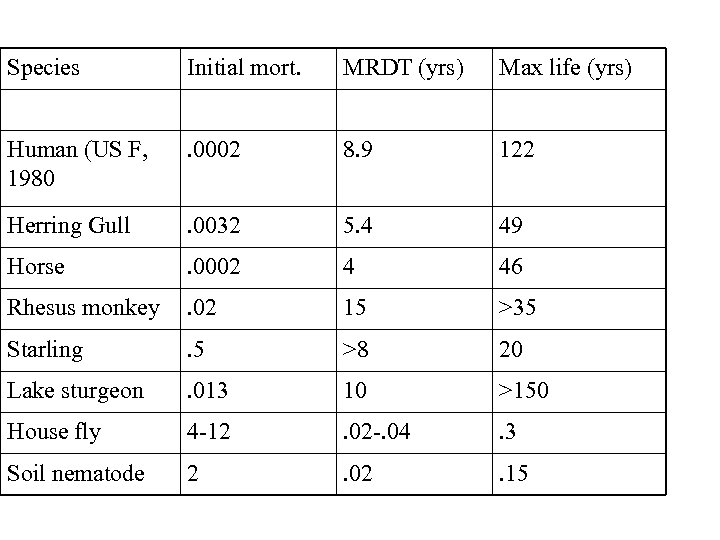Species Initial mort. MRDT (yrs) Max life (yrs) Human (US F, 1980 . 0002 8. 9 122 Herring Gull . 0032 5. 4 49 Horse . 0002 4 46 Rhesus monkey . 02 15 >35 Starling . 5 >8 20 Lake sturgeon . 013 10 >150 House fly 4 -12 . 02 -. 04 . 3 Soil nematode 2 . 02 . 15

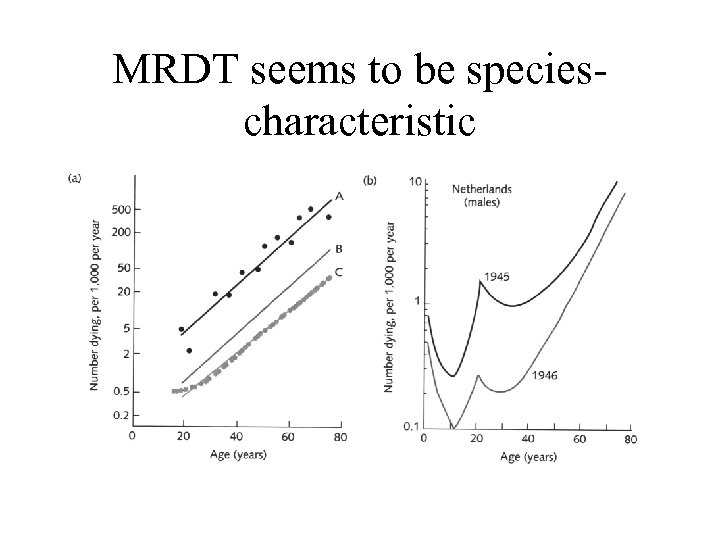MRDT seems to be speciescharacteristic

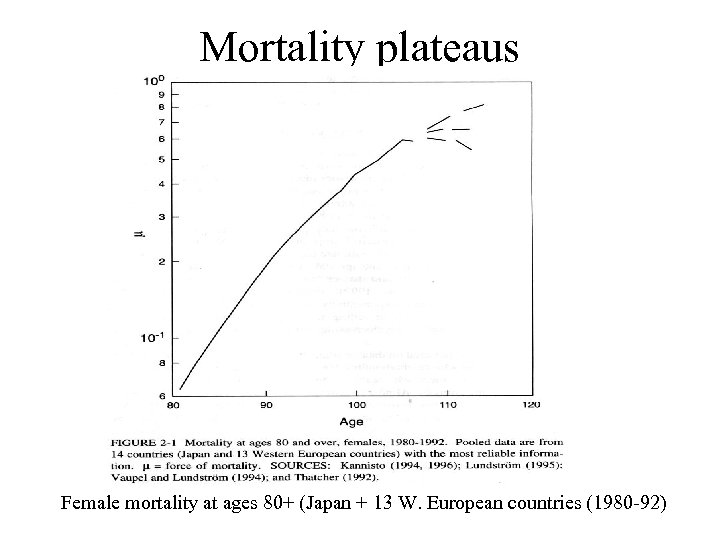Mortality plateaus Female mortality at ages 80+ (Japan + 13 W. European countries (1980 -92)

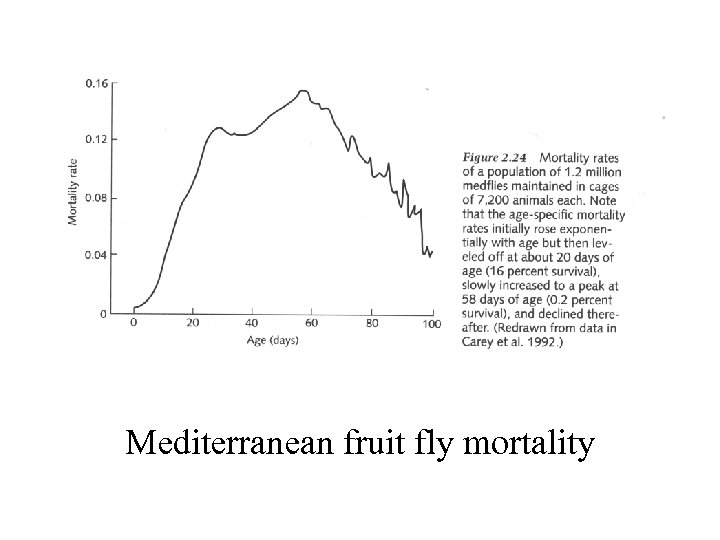Mediterranean fruit fly mortality

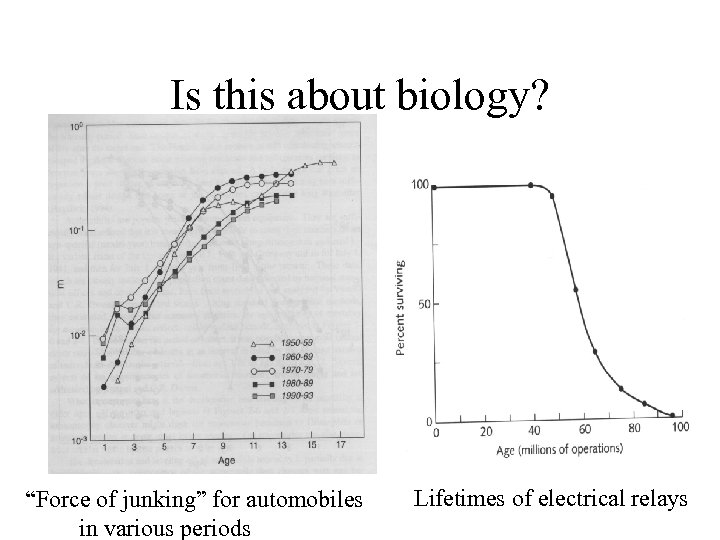Is this about biology? “Force of junking” for automobiles in various periods Lifetimes of electrical relays

What is a Markov process? A stochastic process Xt (where t is time, usually taken to be the positive reals) such that if you know the process up to a given time t, the behavior after time t depends only on the state at time t. The process may be killed, either randomly (at a rate depending on the current position) or instantaneously when it hits a certain part of the state space.

Lessons for young scientists from reviewing the Markov mortality model literature • It’s easy to get your work published if your model reproduces known phenomena…

Lessons for young scientists from reviewing the Markov mortality model literature • It’s easy to get your work published if your model reproduces known phenomena… • … even if you put them in (decently concealed) with your assumptions…

Lessons for young scientists from reviewing the Markov mortality model literature • It’s easy to get your work published if your model reproduces known phenomena… • … even if you put them in (decently concealed) with your assumptions… • … and even if the mathematics is wrong.

“Challenge to homeostasis” (B. Strehler, A. Mildvan 1960) • “The rate of decrease of most physiologic functions of human beings is between 0. 5 and 1. 3 percent per year after age 30, and is fit as well by a straight line as by any other simple mathematical function”. • “Challenges” come at constant rate. • Death occurs when a challenge exceeds the organism’s “vital capacity”. • “Challenges” follow the Maxwell-Boltzmann distribution: Exponentially distributed.

“Challenge to homeostasis” (B. Strehler, A. Mildvan 1960) • “Predicts” the Gompertz curve. • “Predicts” the “nonintuitive” fact that initial mortality and rate of aging are inversely related. • Problem: The exponential rate was built into the assumptions, for which there is no external basis.

Extreme-value theory • J. D. Abernethy (J. Theor. Biol. 1979): Model organisms by independent “systems”, which all fais at the same random rate. “Death” is the time of the first failure. • Proves that such an organism could have exponentially increasing death rates. • Claims (in the nonmathematical introduction and conclusion) that this is the generic situation, which will arise whenever the hazard rates of the components are nondecreasing, which is untrue. (In fact, the individual components would also have to have exponential hazard rates. ) • Still gets cited.

Reliability theory • M. Witten (1985): large number (m) of critical components; death comes when all fail. • Components are independent. Fail with constant rate. • Derives hazard rate approximately m·exp( t).

Reliability theory • M. Witten (1985): large number (m) of critical components; death comes when all fail. • Components are independent. Fail with constant rate. • Derives hazard rate approximately m·exp( t). • Unmentioned: is negative, so the hazard rate decreases exponentially

More reliability theory: Gavrilov & Gavrilova (1990) • • m critical organs, each with n redundant components. Organ fails when all components fail. Death comes when any organ fails. Components fail independently with constant exponential rate. Derive Weibull hazard rates (power law). Want Gompertz hazard rates. Declare that biological systems have most of their components nonfunctioning from the beginning: Number of functioning components in each organ is Poisson. • The exponential of the Poisson then provides the exponential hazard rates.

Biological problems with G&G • • Arbitrary. Where are the missing components? What are the missing components? Theory seems to predict that nearly all organisms should be born dead, with Gompertz mortality only conditioned on the rare survivors.

Small mathematical problem with G&G model:

Big mathematical problem with G&G model: The computation is wrong.

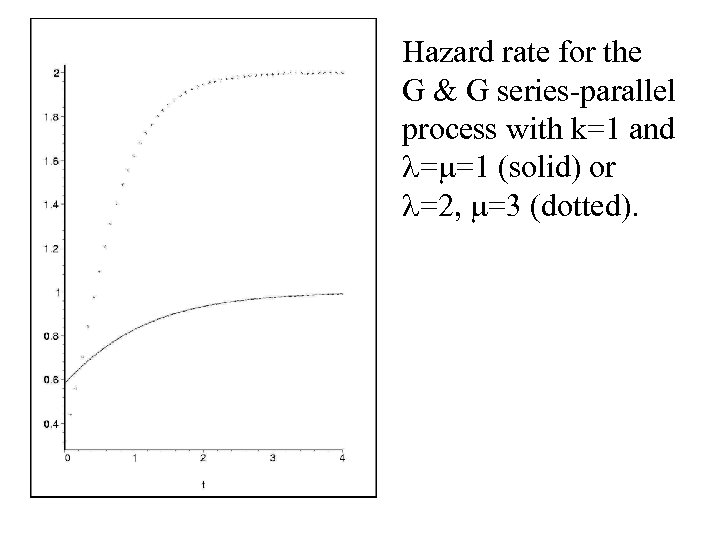Hazard rate for the G & G series-parallel process with k=1 and = =1 (solid) or =2, =3 (dotted).

H. Le Bras’s “cascading failures” model • • Start at senescence state Xt=1. Rate of jumps to next higher state is Xt. Rate of dying is Xt. Le Bras (1976) pointed out that when >> , the mortality rate is about e t for small t. • True… but a little cheap. When >> , the system behaves like a deterministic system d Xt/dt= Xt. State is Xt e t.

H. Le Bras’s “cascading failures” model • In fact, as Gavrilov & Gavrilova pointed out (1990) the result is even better when you don’t assume >>. By this time, mortality plateaus had been recognized. The general hazard rate is ( + )t( + e( + )t)-1, ( + ) e which is a nice logistic Gompertz curve, with plateau at +.

H. Le Bras’s “cascading failures” model • But… the exponential is still in the assumptions. • Also, the assumptions are quite specific and arbitrary.

Attempts to explain the Gompertz curve with Markov models have been successful only when: • The exponential increase was built into the assumptions in a fairly transparent way or • The computations were wrong.

What about mortality plateaus? Suggested explanations: 1. Heterogeneity in the population: selection. (Analyzed in DS: “Estimating mortality rate doubling times”. Available as preprint. ) 2. Individuals actually deteriorate more slowly at advanced ages.

What about mortality plateaus? • J. Weitz and H. Fraser (PNAS 2001) did explicit computation for Brownian motion with constant downward drift, killed at 0. It shows “senescence” and “plateaus” -hazard rates increase rapidly (though not exponentially) at first, but eventually converge to a finite nonzero constant.

Criticisms of Weitz-Fraser • The assumptions (constant diffusion rate, constant downward drift, killing only at 0) are very specific. • The assumptions have little empirical justification. • The methods cannot be generalized to any other case.

Criticisms of Weitz-Fraser • The assumptions (constant diffusion rate, constant downward drift, killing only at 0) are very specific. • The assumptions have little empirical justification. • The methods cannot be generalized to any other case. • For understanding anything other than the plateaus, the model is too general: By choosing the starting distribution, the hazard rate can become almost anything, as long as it eventually converges to a rate ≤ b 2/2. (Here b is the rate of negative drift. )

In fact, the result is very general. • Killed markov processes (which also may be thought of as submarkov processes) converge under fairly general conditions to quasistationary distributions. That is, The hazard rate will also converge to the rate of killing in this distribution.

Some Theorems • Let Xt be a diffusion on a one-dimensional interval with drift b and variance 2, so satisfying the SDE d. Xt= (Xt)d. Wt + b(Xt)dt, and killed at the rate k(Xt). Let be the smallest such that there is a positive solution to ( )"—(b )'—k =— .

Some Theorems • If both boundaries are regular then the distribution of Xt, conditioned on survival converges to density , and the mortality rate converges to . • If ∞ is a natural or entrance boundary and r 1 regular, then this convergence still holds if (*) • In the above, condition (*) may be replaced by lim k(z)> . z ∞

Interpretation • Mortality rates level off, not because the process is changing, or because of selection on populations with heterogeneous frailties. The individuals who happen to survive a long time simply tend to have a distribution of vitality states which are somewhat spread out, not arbitrarily piled up near points of killing.

Why are there mortality-rate plateaus? Suggested explanations: 1. Heterogeneity in the population: selection. 2. Individuals actually deteriorate more slowly at advanced ages. 3. Those alive at advanced ages are, purely by chance, inclined to be more fit than the bare minimum required to stay alive.

For more information, see “Markov mortality models: implications of quasistationarity and varying initial distributions” by DS and Steven Evans. (Available as a preprint. )

Evolutionary theories • Is mortality a trait shaped by natural selection? • No “overdesigned parts”. • Medawar, Hamilton: Mutation-selection equilibrium. • Antagonistic pleiotropy. • Kirkwood: Disposable soma.

Can evolutionary theory explain Gompertz curve? Mortality plateaus? • Charlesworth says yes to Gompertz. • Mueller and Rose say yes to mortality plateaus.

Charlesworth: Mutation-selection equilibrium • Not an evolutionary optimum. • B. Charlesworth: for rare deleterious genes, equilibrium frequency should be inversely proportional to evolutionary cost. • In state of nature, most mortality is exogenous, so should come with constant rate . Evolutionary cost of a mutation that kills at age x should be like e- x.

Problems with Charlesworth’s model • Requires most aging to depend on genes with age-specific effects. • What happens when you iterate? (So far, only simulations. ) • Doesn’t allow for gene interactions. • What is exogenous mortality really?

Mueller and Rose on mortality plateaus. • State space of age-specific mortality rates for 100 days. • Random “mutations” act over 2 randomly chosen ranges of days. ( =1 or 40) • In beneficial range • In harmful range • Mutant either vanishes or become fixed. Probability depends on change in fitness.

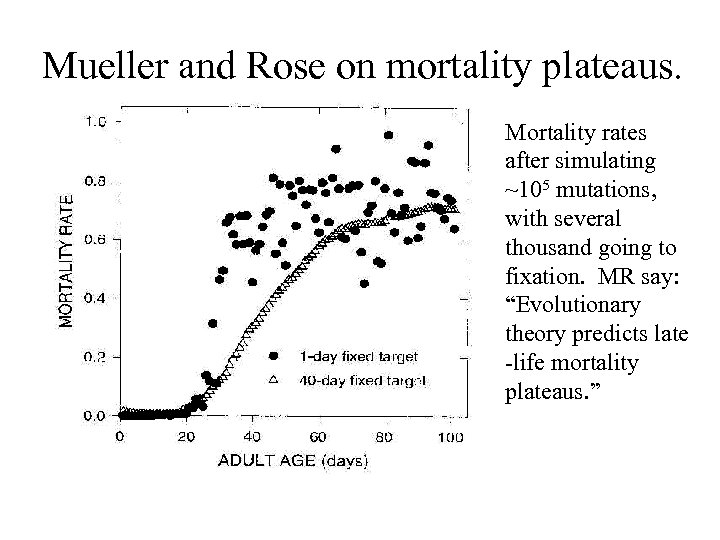Mueller and Rose on mortality plateaus. Mortality rates after simulating ~105 mutations, with several thousand going to fixation. MR say: “Evolutionary theory predicts late -life mortality plateaus. ”

Ken Wachter pointed out that the graphs on MR’s paper show transient states of the population. They didn’t run the simulations long enough to reach equilibrium. Selection reduces mortality first at low ages, and only later starts to transfer mortality from intermediate to higher ages. If you stop early, it looks like a plateau. Lesson: Simulate, but verify.

http: //www. demog. berkeley. edu/ ~dstein/agingpage. html