Stochastic Geometry as a tool for the modeling

Stochastic Geometry as a tool for the modeling of telecommunication networks Prof. Daniel Kofman, ENST - Telecom Paris Dr. Anthony Busson IEF – University of Orsay-Paris 11 TAU – 25/11/2004 1

S. G. and Network Modeling n When modeling a network, two main types of characteristics need to be captured: ¡ the dynamics imposed by the traffic evolution at different time scales n ¡ time properties the spatial distribution and movement of network elements (terminals, antennas, routers, etc. ) n geometric properties 2

Examples of Geometric Properties n Modeling of ¡ UMTS/Wi. Fi antennas location n ¡ Sensor networks n ¡ ¡ ¡ ¡ optimal cost under coverage constraints optimal cost under coverage, connectivity and lifetime constraints Ad-Hoc Networks CDN servers location for optimal content distribution Multicast capable routers of a CBT architecture Reliable Multicast Servers for optimal retransmission of missed information Networks Interconnection points Optimal placement of fix access networks concentrators Others 3

Why Stochastic Geometry n The efficiency of a protocol/mechanism/ dimensioning rule, etc. depends on its adaptability to different network topologies and users distribution ¡ The performance metrics of interest have usually to be obtained as an average over n n A large set of possible network topologies A large set of possible users location distribution ¡ ¡ n Members of the various multicast groups Clients of the different available content A large set of users behaviors ¡ ¡ Mobility Content popularity 4

Content n Introduction ¡ ¡ n A Simple example to illustrate what S. G. is ¡ n n n Application domains in the telecommunication world Why Stochastic Geometry (S. G. )? Network infrastructure optimization Theoretical framework, part 1 – Tessellation processes Other application examples (CDNs, Multicast routing) Theoretical framework, part 2 – Coverage processes More application examples (CDMA, Ad-hoc and sensor networks) Summary: Main mathematical objects, Main known results Conclusions and Perspectives 5

Content n Introduction ¡ ¡ n A Simple example to illustrate what S. G. is ¡ n n n Application domains in the telecommunication world Why Stochastic Geometry (S. G. )? Network infrastructure optimization Theoretical framework, part 1 – Tessellation processes Other application examples (CDNs, Multicast routing) Theoretical framework, part 2 – Coverage processes More application examples (CDMA, Ad-hoc and sensor networks) Summary: Main mathematical objects, Main known results Conclusions and Perspectives 6

A simple example: Network infrastructure optimization n Network topology to be modeled: ¡ ¡ Users are connected to the closest Service Provider Point of Presence (Po. P) Po. P are hierarchically connected to the closest concentrator Higher layer concentrators are connected to the closest core equipment Core equipment are “meshed” 7

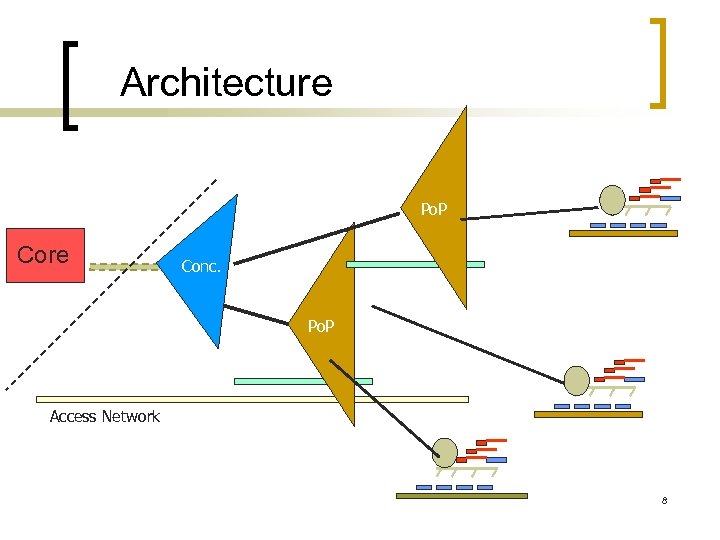Architecture Po. P Core Conc. Po. P Access Network 8

Clients are represented by a Point Process on the plane 9

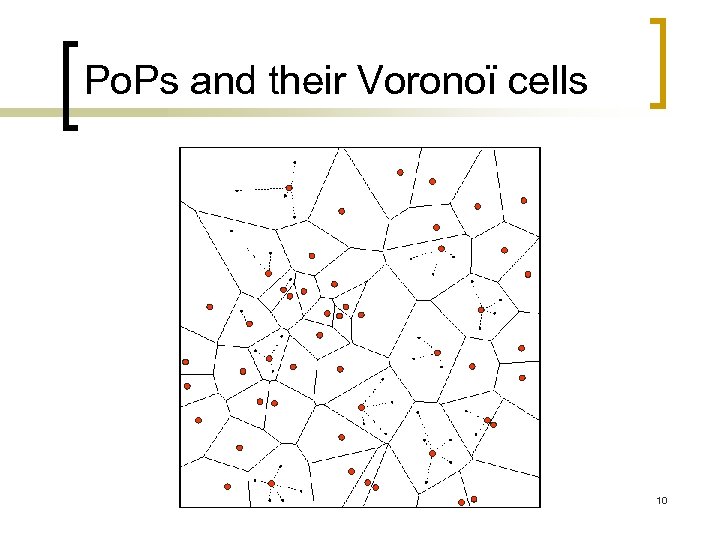Po. Ps and their Voronoï cells 10

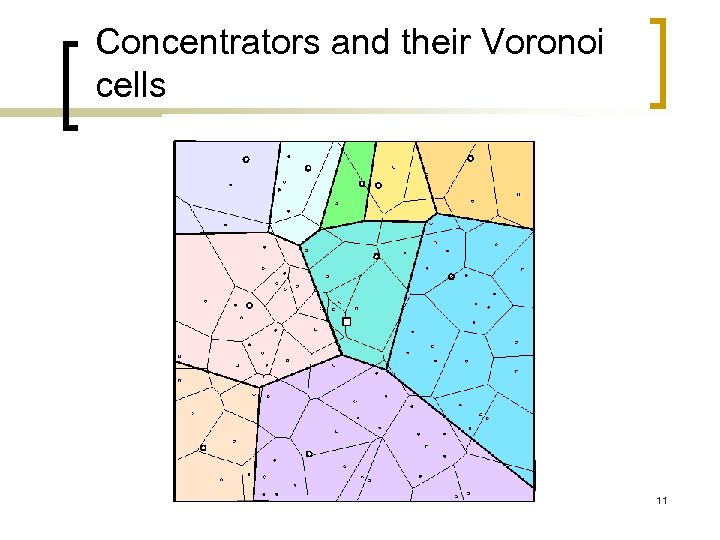Concentrators and their Voronoi cells 11

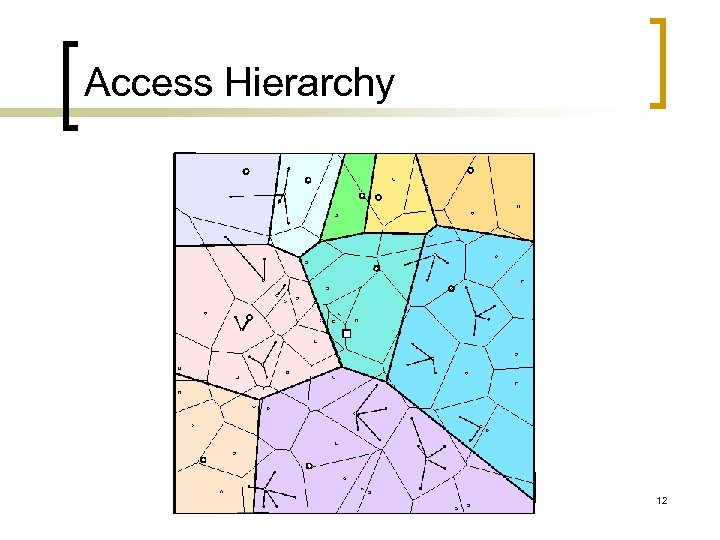Access Hierarchy 12

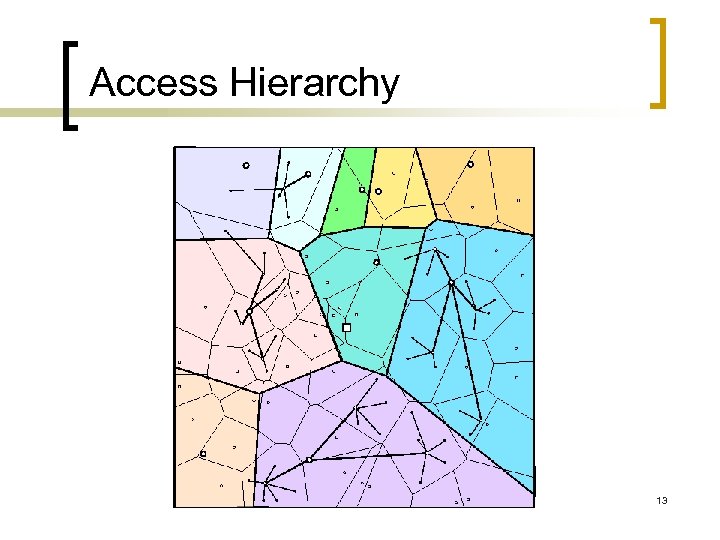Access Hierarchy 13

Delaunay Graph 14

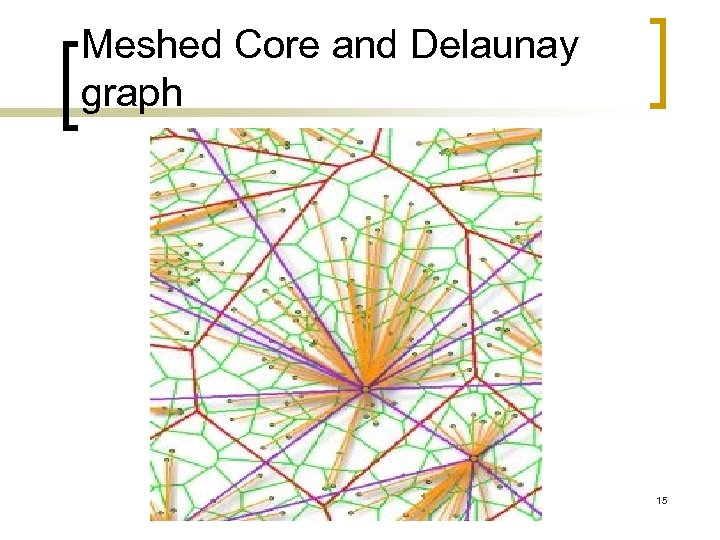Meshed Core and Delaunay graph 15

Questions we can answer n For a given distribution of users and for a given cost function, under Poisson hypothesis, we can compute the ¡ ¡ ¡ n Optimal number of hierarchical levels Optimal intensity of the various point processes Average number of users per Po. P Average cost of the network Routing cost in number of hops when connection two clients as a function of their distance For the detailed analysis of this model see ¡ F. Baccelli, M. Klein, M. Lebourges, and S. Zuyev. Stochastic geometry and architecture of communication networks. J. Telecommunication Systems, 7: 209 -227, 1997. 16

Content n Introduction ¡ ¡ n A Simple example to illustrate what S. G. is ¡ n n n Application domains in the telecommunication world Why Stochastic Geometry (S. G. )? Network infrastructure optimization Theoretical framework, part 1 – Tessellation processes Other application examples (CDNs, Multicast routing) Theoretical framework, part 2 – Coverage processes More application examples (CDMA, Ad-hoc and sensor networks) Summary: Main mathematical objects, Main known results Conclusions and Perspectives 17

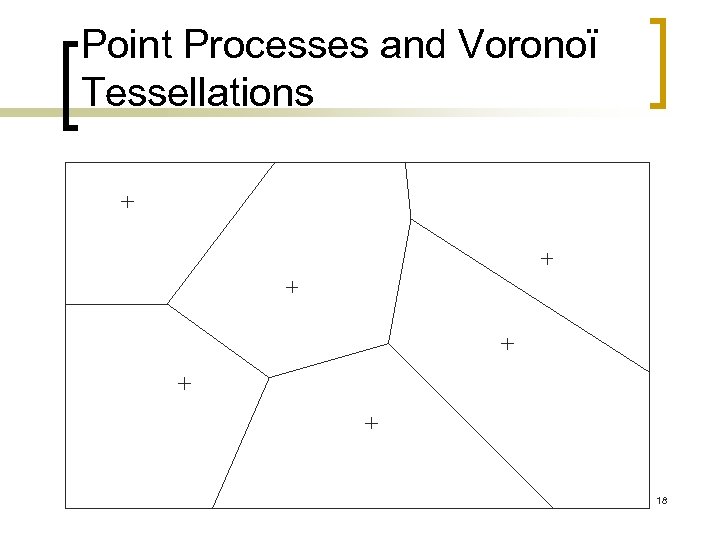Point Processes and Voronoï Tessellations 18

Stationary Poisson point process in d n Definition ¡ ¡ n The number of points in a set B of d follows a discrete Poisson law of parameter . ||B||, where is the intensity of the process Let B 1…Bn be disjoint sets of d, the number of points in B 1 … B 2 are independent. Consequence ¡ Given n the number of points in B, the points are independently and uniformly distributed in B. 19

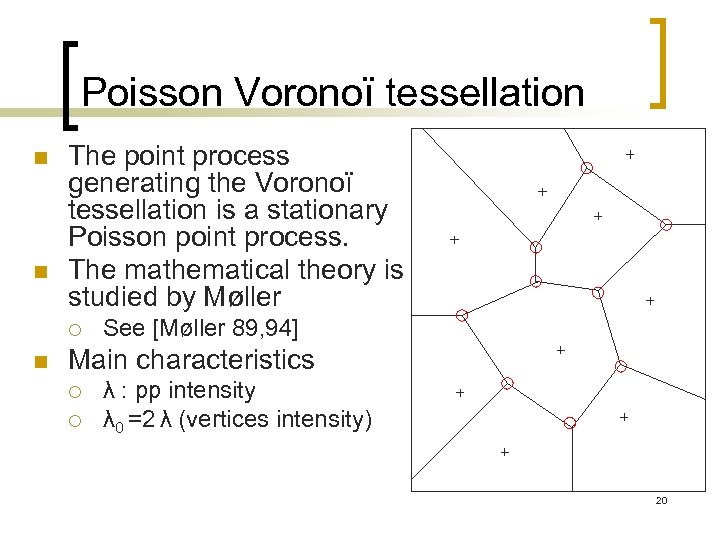Poisson Voronoï tessellation n n The point process generating the Voronoï tessellation is a stationary Poisson point process. The mathematical theory is studied by Møller ¡ n See [Møller 89, 94] Main characteristics ¡ ¡ λ : pp intensity λ 0 =2 λ (vertices intensity) 20

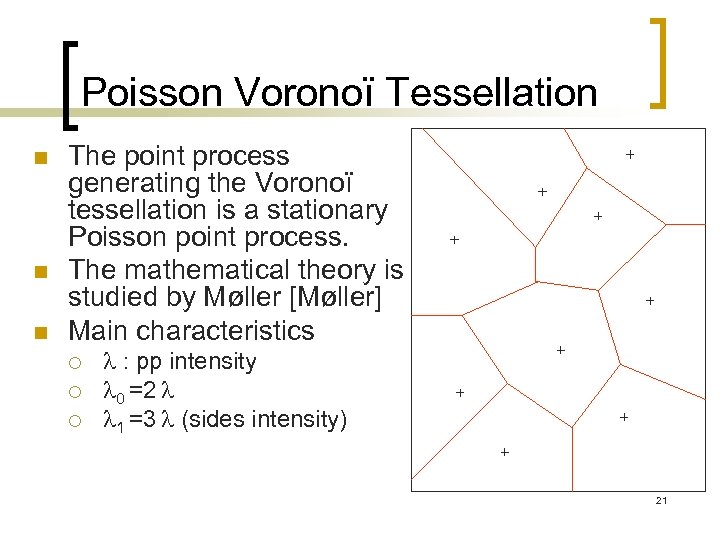Poisson Voronoï Tessellation n The point process generating the Voronoï tessellation is a stationary Poisson point process. The mathematical theory is studied by Møller [Møller] Main characteristics ¡ ¡ ¡ : pp intensity 0 =2 1 =3 (sides intensity) 21

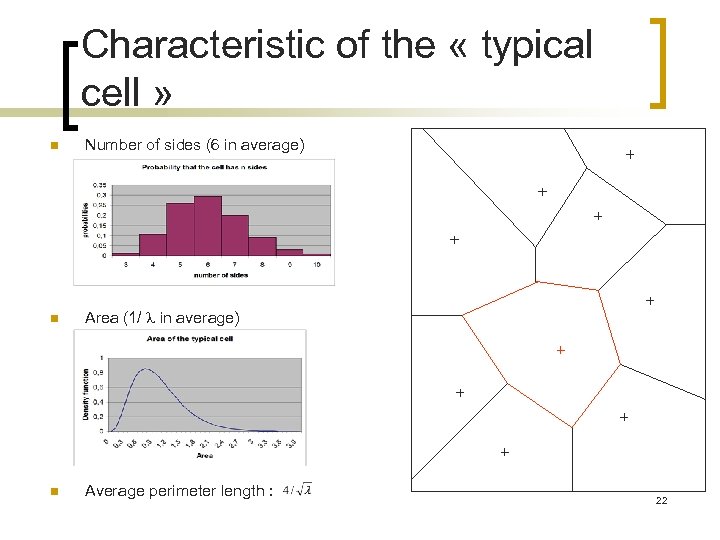Characteristic of the « typical cell » n Number of sides (6 in average) n Area (1/ in average) n Average perimeter length : 22

Cost function n A point at x add a cost f(x, N). In this case, the mean of the cost function is: n By the refined Campbell formula, we have: n Expectation under Palm measure 23

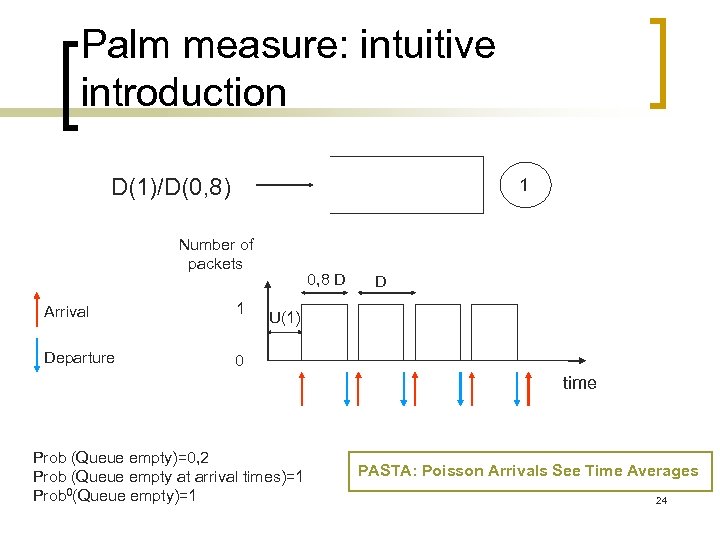Palm measure: intuitive introduction D(1)/D(0, 8) 1 Number of packets Arrival 1 Departure 0, 8 D D 0 U(1) time Prob (Queue empty)=0, 2 Prob (Queue empty at arrival times)=1 Prob 0(Queue empty)=1 PASTA: Poisson Arrivals See Time Averages 24

Feller’s Paradox for a Poisson Process n n n n Bus inter-arrival process: Poisson of parameter Bus inter-arrival times sequence: i. i. d. , exp( ) Waiting time for a passenger arriving at time t: exp( ) Time since last bus arrival before time t: exp( ) Probability distribution of the inter-arrival containing time t: Erlan-2 of parameter Average inter-arrival time 1/ Average length of the inter-arrival containing time t: 2/ t 25 time

Feller’s paradox and Palm theory n n n Since we look at stationary processes, time t could be whatever. We will concentrate without loss of generality in the case t=0. By definition of Palm probability (at time 0), we have ¡ ¡ n Prob 0(T 0=0) = 1 The inter-arrival time sequence is i. i. d. , exp( ) Since the intervals generated by each point of the process are equivalent, we can concentrate in any of them, like the one starting at 0, when analyzing the performances of the system. 26

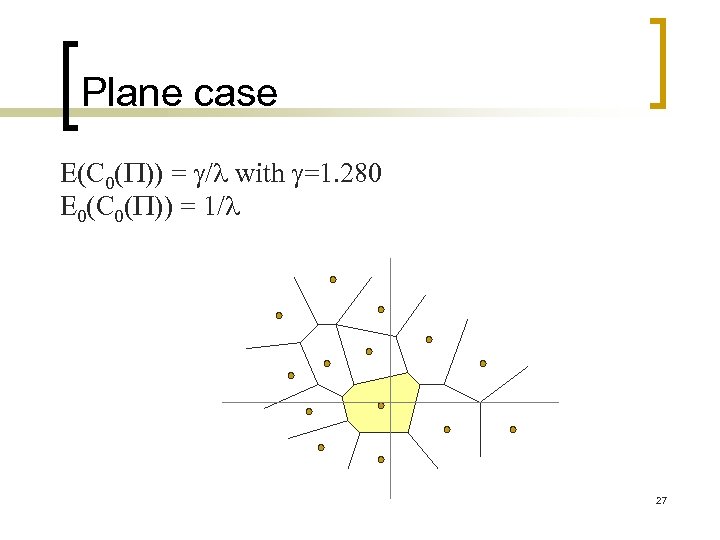Plane case E(C 0( )) = / with =1. 280 E 0(C 0( )) = 1/ 27

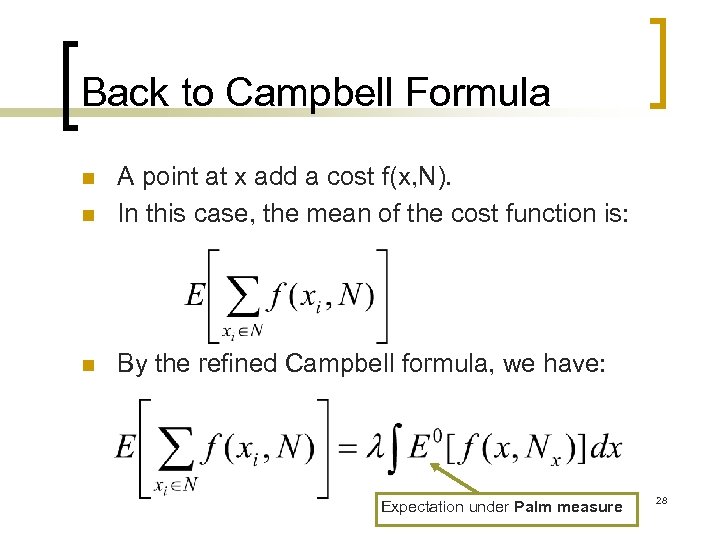Back to Campbell Formula n A point at x add a cost f(x, N). In this case, the mean of the cost function is: n By the refined Campbell formula, we have: n Expectation under Palm measure 28

Summary n n n The location of the various elements is modeled by point processes Voronoï Tessellations are used to partitioning the plane and deducing the elements connectivity Delaunay graph/tessellations can be used for the same purposes A cost function is defined as a functional of the previous processes Palm theory is used to evaluate this cost function we want to optimize 29

Content n Introduction ¡ ¡ n A Simple example to illustrate what S. G. is ¡ n n n Application domains in the telecommunication world Why Stochastic Geometry (S. G. )? Network infrastructure optimization Theoretical framework, part 1 – Tessellation processes Other application examples (CDNs, Multicast routing) Theoretical framework, part 2 – Coverage processes More application examples (CDMA, Ad-hoc and sensor networks) Summary: Main mathematical objects, Main known results Conclusions and Perspectives 30

Example 2: Content Distribution Internet User Content Provider Server 31

Content Delivery Network n Problems : ¡ The provided Qo. S depends on the network performances n ¡ n Thus, the content provider cannot control this quality The content on the cash servers cannot be controlled Solution : ¡ To deploy a set of servers n ¡ Expensive To share the resources of a CDN between various Content Providers 32

What is the optimal location of the CDN servers ? Internet Users Content Providers 33

The role of Stochastic Geometry n Dimensioning difficulty: several parameters are not known a priori ¡ ¡ ¡ Clients evolution – Content Providers location and content Number and location of users Popularity of content Network topology Network distribution cost 34

A Simplified Stochastic Model n A point process will represent the various possible server locations (ISPs, etc. ) ¡ n Two marks are associated with each point ¡ ¡ n A non Euclidian distance can be used, like the transmission cost The fist one indicates the number of users associated with the corresponding point (ISP, etc. ) The second one indicates whether a server is deployed in the corresponding point or not A function of the distance between each client and the nearest server describes the Qo. S perceived by the users ¡ A non Euclidian distance can be used, like the transmission cost 35

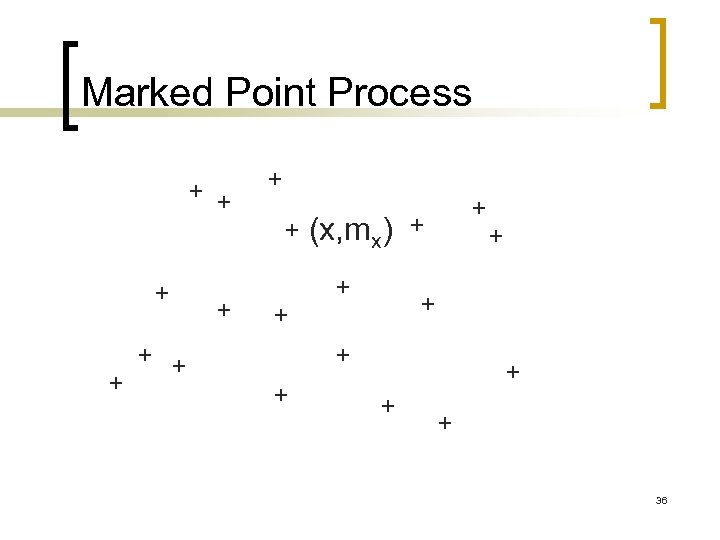Marked Point Process (x, mx) 36

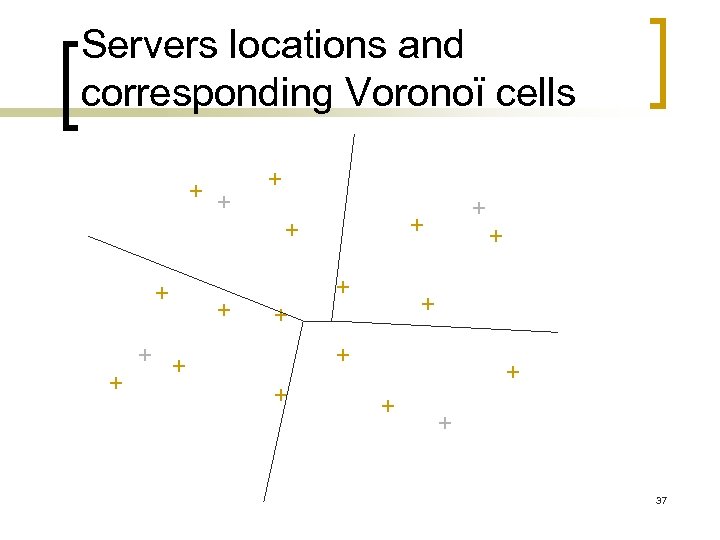Servers locations and corresponding Voronoï cells 37

Cost Function n From the Qo. S point of view, the best solution is to deploy servers in each available location This approach leads to a high CAPEX and OPEX The cost function we optimize will consider ¡ ¡ ¡ The cost of the servers, denoted by α (we denote the number of servers by S) The number of users at point j, denoted by mj (we denote by L the set of possible locations) A measure of the Qo. S degradation, denoted by f(xj), where xj is the distance between the users that are related with location j and their nearest server. Cost 38

A more general model n Several server classes can be considered ¡ ¡ n n Servers of different classes have different cost E. g. Many small servers for a reduced number of very popular content and a reduced number of big servers for the less popular content Each object is located in a server of a given class Different location policies can be implemented ¡ ¡ ¡ Based on objects popularity Random Others 39

Main Results ¡ ¡ Optimal intensity of the point processes representing the different classes of servers Analysis of the impact of the various parameters on the performances of the system Evaluation of the cost of the CDN For a detailed analysis of this model see n A. Busson, D. Kofman and Jean-Louis Rougier Optimization of Content Delivery Networks server placement, International Teletraffic Congress, ITC-18, 2003 40

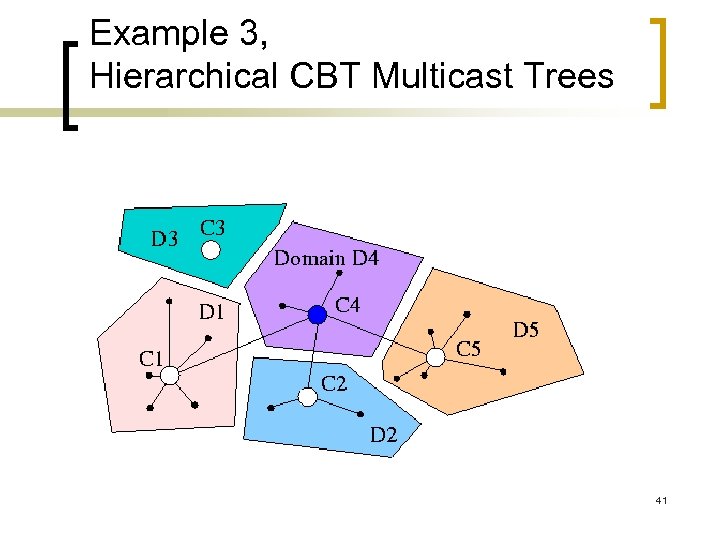Example 3, Hierarchical CBT Multicast Trees 41

Point Process on the place representing routers location 42

Stochastic Geometry Model n n n Routers are represented by a Point Process in the plane The routers participating to the tree are obtained by thinning the previous point process « Rendez-vous » (RP) points are modeled by independent point process of lower intensity ¡ RP are active if they have an active router (RV point of the lower level) in their Voronoi cell 43

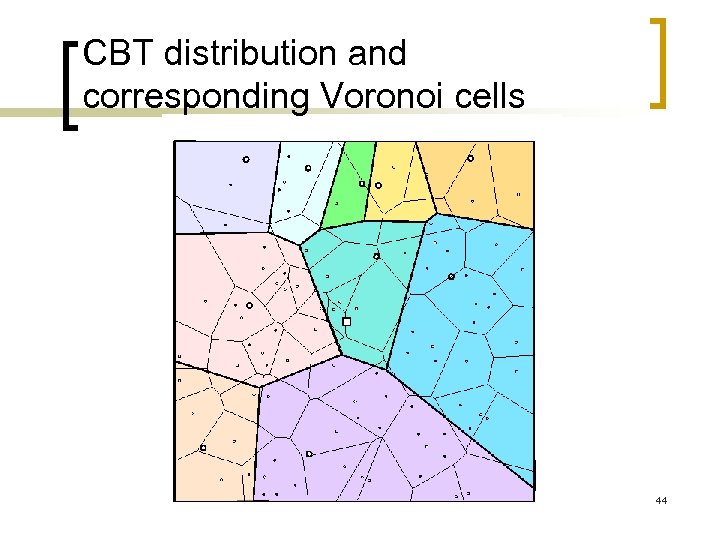CBT distribution and corresponding Voronoi cells 44

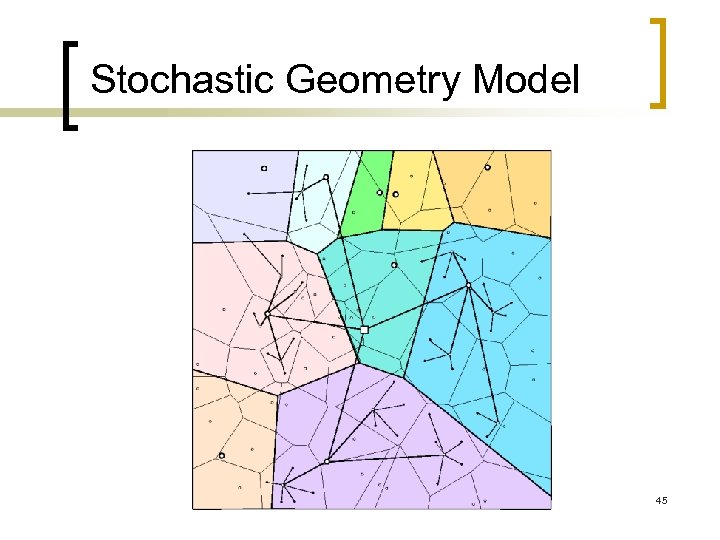Stochastic Geometry Model 45

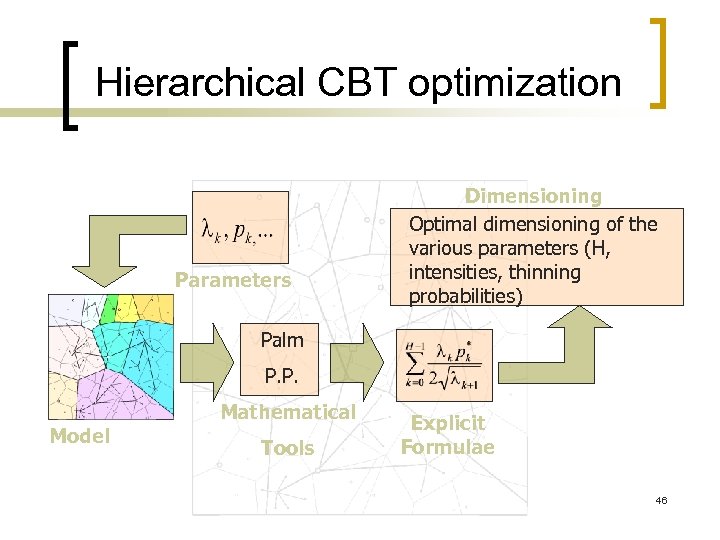Hierarchical CBT optimization Parameters Dimensioning Optimal dimensioning of the various parameters (H, intensities, thinning probabilities) Palm P. P. Model Mathematical Tools Explicit Formulae 46

Reference n For a detailed analysis of this model see: ¡ F. Baccelli, D. Kofman, J. L. Rougier, « Self. Organizing Hierarchical Multicast Trees and their Optimization » , IEEE Infocom'99, New-York (E. U. ), March 1999 47

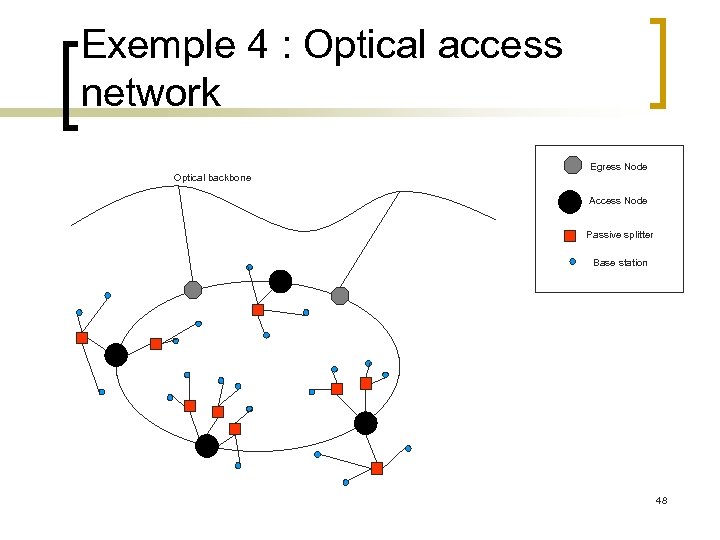Exemple 4 : Optical access network Egress Node Optical backbone Access Node Passive splitter Base station 48

Evaluation of optical access network n n n Ø Estimate the cost P of a ring N ring access networks may be evaluated as NP If the ring intensity is λ, the cost of a network covering A is λ||A||P The problem is reduced to the estimation of the cost of a typical ring architecture. 49

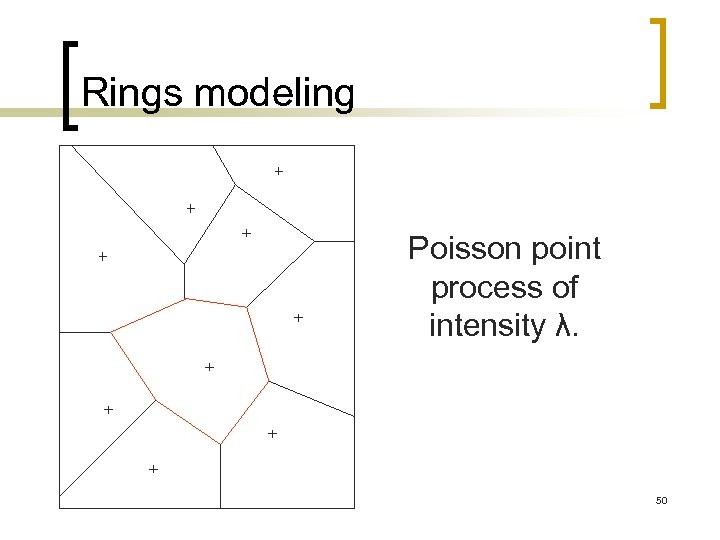Rings modeling Poisson point process of intensity λ. 50

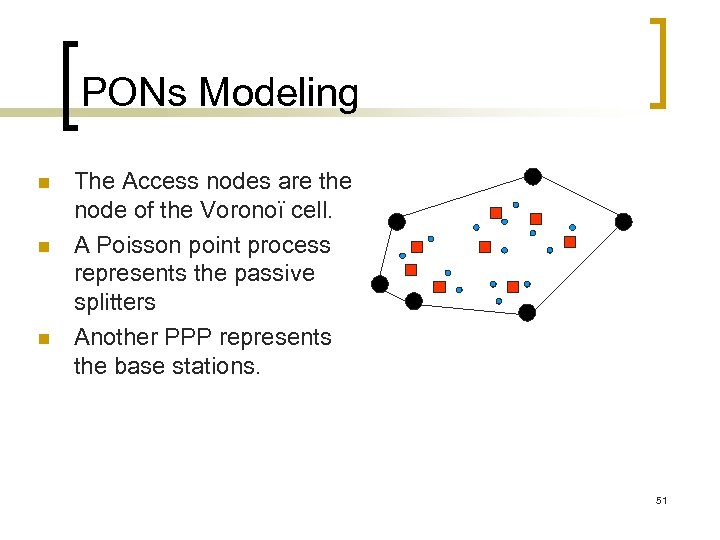PONs Modeling n n n The Access nodes are the node of the Voronoï cell. A Poisson point process represents the passive splitters Another PPP represents the base stations. 51

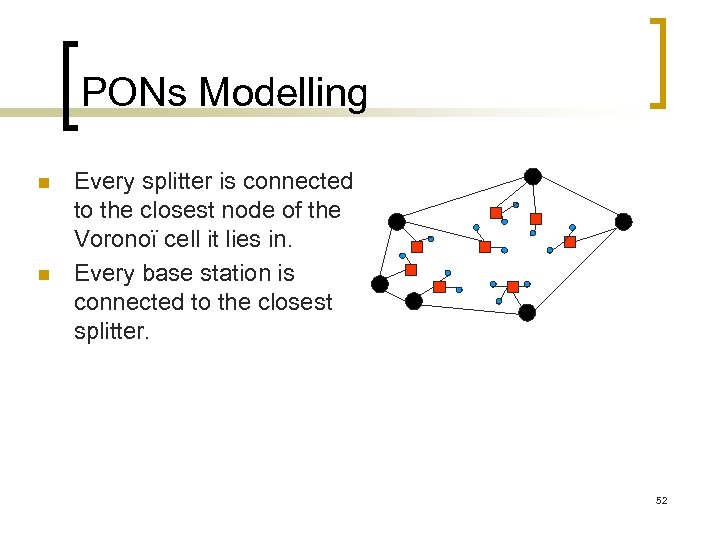PONs Modelling n n Every splitter is connected to the closest node of the Voronoï cell it lies in. Every base station is connected to the closest splitter. 52

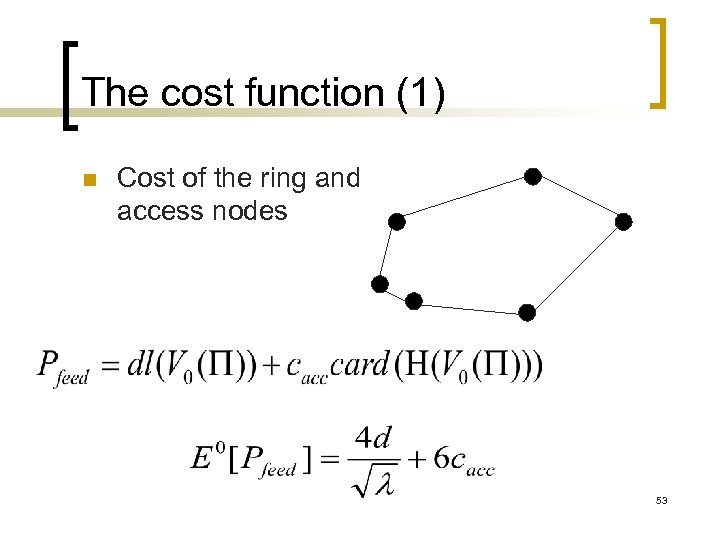The cost function (1) n Cost of the ring and access nodes 53

The cost function (2) n Cost of the splitters 54

The cost function (3) n Cost of the base stations 55

Conclusions for the example 4 n n Economical studied of the access network Evaluation of the costs with regard to the number of equipment ¡ ¡ ¡ n n access nodes splitters base stations Evaluation of the optimal intensities describing the different equipments For a detailed analysis of this model see: ¡ C. Farinetto, S. Zuyev, “Stochastic geometry modelling of hybrid optical networks”, Performance Evaluation 57, 441452, 2004. 56

Content n Introduction ¡ ¡ n A Simple example to illustrate what S. G. is ¡ n n n Application domains in the telecommunication world Why Stochastic Geometry (S. G. )? Network infrastructure optimization Theoretical framework, part 1 – Tessellation processes Other application examples (CDNs, Multicast routing) Theoretical framework, part 2 – Coverage processes More application examples (CDMA, Ad-hoc and sensor networks) Summary: Main mathematical objects, Main known results Conclusions and Perspectives 57

Dual problem n Tessellation: the process define the geometry properties of a way to partition the plane from which the topology of the network is deduced ¡ n The connectivity between neighbors equipment is deduced from the geometric properties of the processes Coverage: the processes defined the topology of the network from which the geometry of the coverage of the plane is deduced ¡ The geometric properties we are interested on are deduced from the connectivity properties between neighbors equipment (like those deduced from the radio channel model) 58

Coverage processes n Motivation ¡ Historical applications n n ¡ Structure of the paper Distribution of the heather in a forest Modeling the crystallization in metals Etc Modeling of communication systems n n n Modeling node and connectivity of an ad-hoc network Modeling the coverage of a CDMA network Modeling coverage and connectivity in sensor networks Routing in ad-hoc networks Others 59

Boolean Model-Definition 60

Boolean model - example 61

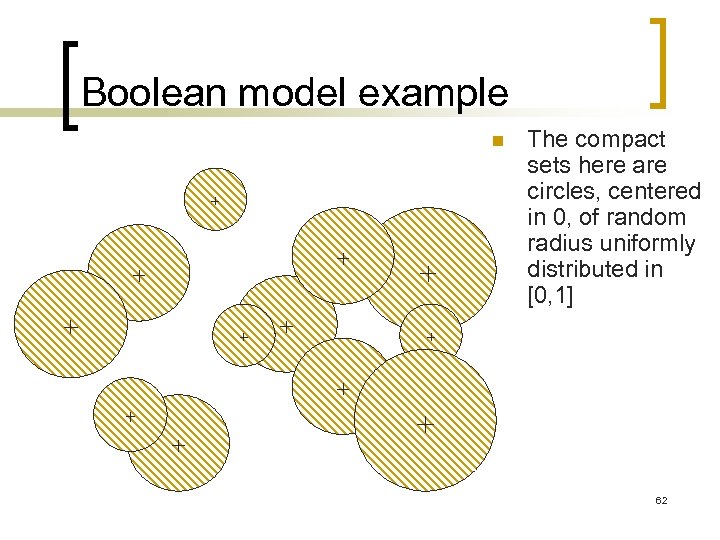Boolean model example n The compact sets here are circles, centered in 0, of random radius uniformly distributed in [0, 1] 62

Capacity functional n Probability that the intersection between the Boolean model Ξ and a finite closed set K is not empty n The capacity functional determines uniquely the distribution of the Boolean model. ¡ n Where n 2 is the Lebesgue measure in the plane Remark: the probability of K being covered is not known in general ¡ Of course it is when K is a singleton set 63

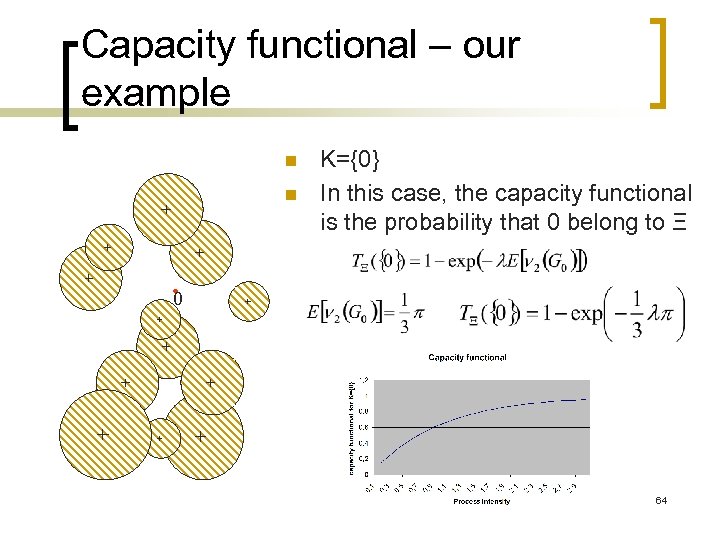Capacity functional – our example n n K={0} In this case, the capacity functional is the probability that 0 belong to Ξ 0 64

Contact distribution function n If a point is not covering by Ξ, how far is the boolean model? Let’s take B(R)=B(0, R) a test set covering 0 We define 65

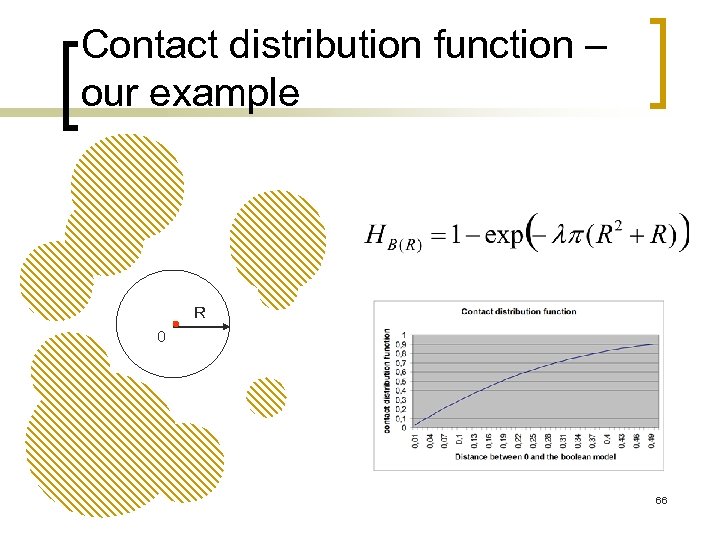Contact distribution function – our example R 0 66

Content n Introduction ¡ ¡ n A Simple example to illustrate what S. G. is ¡ n n n Application domains in the telecommunication world Why Stochastic Geometry (S. G. )? Network infrastructure optimization Theoretical framework, part 1 – Tessellation processes Other application examples (CDNs, Multicast routing) Theoretical framework, part 2 – Coverage processes More application examples (CDMA, Ad-hoc and sensor networks) Summary: Main mathematical objects, Main known results Conclusions and Perspectives 67

CDMA Coverage - Boolean Model 68

Example 69

Known results 70

CDMA coverage Model 71 Remark: Not a Boolean model since the compact sets are not independent

CDMA coverage Model 72

What can we calculate n n Coverage probability Distribution of the number of cells covering a given location 74

Conclusions on the CDMA coverage model n Tool for estimating the network cost ¡ n Tool for predicting the impact of network evolution ¡ n n How many antennas (on average) for a given coverage ? What about coverage when increasing the number of antennas The model can be extended to include random attenuation, correlation between marks, etc. The movement of terminals can be modelled by line processes ¡ ¡ Evaluation of number of hand-overs Evaluation of traffic and required capacity 76

References n For a detailed analysis of these models see: ¡ ¡ ¡ F. Baccelli and B. Blaszczyszyn. On a coverage process ranging from the boolean model to the poisson voronoi tessellation, with applications to wireless communications. Adv. Appl. Prob. , 33(2), 2001. F. Baccelli, B. Blaszczyszyn, and F. Tournois. Spatial averages of coverage characteristics in large CDMA networks. Technical Report 4196, INRIA, June 2001. F. Baccelli and S. Zuyev. Stochastic geometry models of mobile communication networks. In Frontiers in queueing, pages 227 -243. CRC Press, Boca Raton, FL, 1997. 77

Modeling ad-hoc and sensor networks n n Let N be a random variable representing the number of devices For a given realization of N, N points are independently and uniformly distributed in the square of size Lx. L Two points x and y are said to be connected if d(x, y)

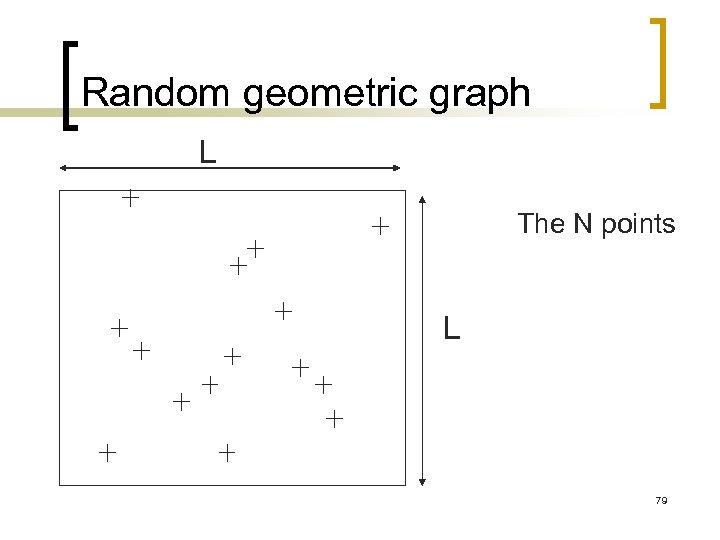Random geometric graph L The N points L 79

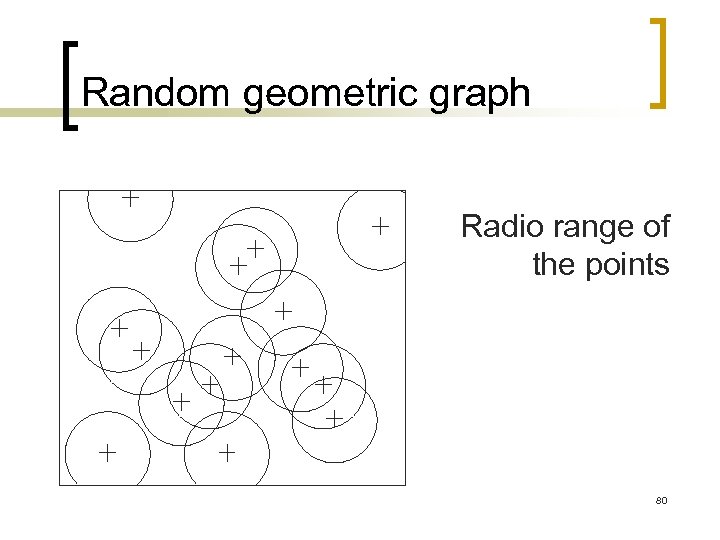Random geometric graph Radio range of the points 80

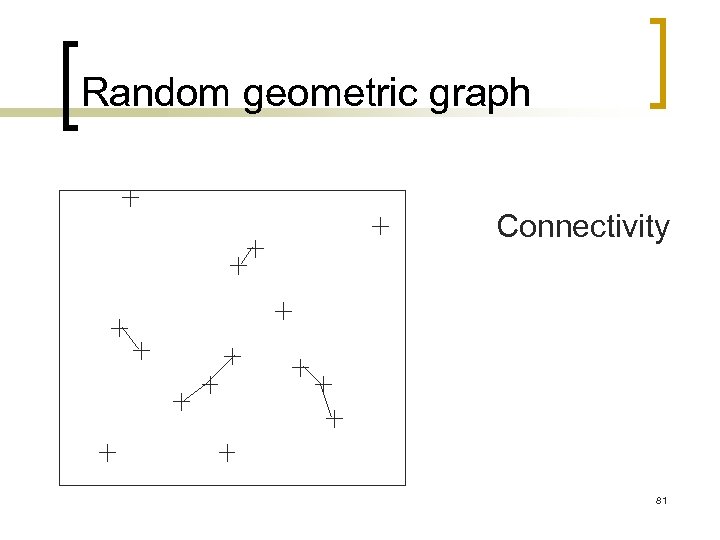Random geometric graph Connectivity 81

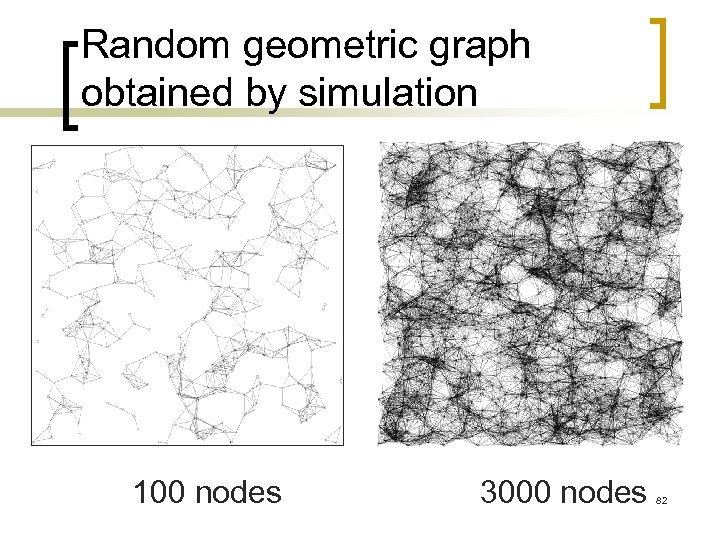Random geometric graph obtained by simulation 100 nodes 3000 nodes 82

Percolation – Finite domain n n A network is said to be fully connected when it exist a path between any pair of nodes What is the probability of the network being fully connected based on the random geometric graph model? ¡ Depends only on the mean number of direct neighbors (mean size of the 1 neighborhoud) 83

Percolation – Finite domain – results n n Let G(n, r(n)) be the random geometric graphs with n points and with radius r(n). Let be Pc(n, r(n)) the probability that all the nodes are connected. 84

Percolation – Finite domain – results n n Determine r(n) such that Pc(n, r(n)) goes to one as n →+∞. Theorem: 85

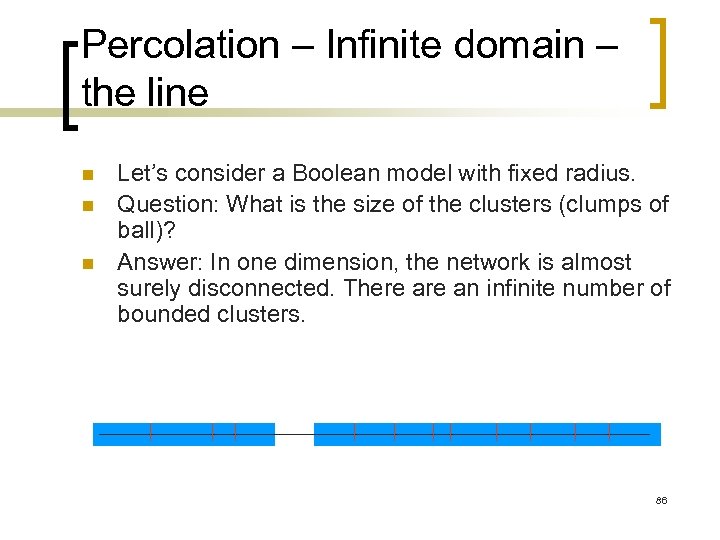Percolation – Infinite domain – the line n n n Let’s consider a Boolean model with fixed radius. Question: What is the size of the clusters (clumps of ball)? Answer: In one dimension, the network is almost surely disconnected. There an infinite number of bounded clusters. 86

Percolation – Infinite domain – the plane n n Let be a Poisson Boolean model in the plane with balls of fixed radius. Theorem [Meester 99]: There exists a critical density λc>0 such that ¡ ¡ If λ<λc, all clusters are bounded almost surely (sub-critical case) If λ>λc, there exists a unique unbounded cluster almost surely (supercritical case) 87

Percolation in a more realistic model n STIRG : Signal to Interference Ration Graph ¡ A node j can receive data from node i iff ¡ Two nodes are neighbors if they can exchange data in both directions 88

Percolation in a more realistic model : results n n When γ=0, it is a boolean model and the previous theorem holds. When γ>0, ¡ ¡ ¡ The number of neighbors is bound. A node can have at most 1+1/ γβ neighbors. Under certains assumptions on the attenuation function l(. ), there exists λc<∞ s. t. for all λ> λc there exists 0<γc(λ) s. t. for γ <γc(λ) the probability that a node belongs to an inifinite cluster is strictly greater than zero. Dousse, Baccelli, Thiran, « Impact of interfernces on connectivity in Ad Hoc Networks » , Infocom 2003. 89

Other interesting problems n n n Optimizing a sensor network composed of heterogeneous devices Taking into account layer 3 routing mechanisms when evaluating an ad-hoc or sensor network connectivity Taking into account the MAC layer and radio channel properties when modeling sensor networks Link with graph theory (e. g. small worlds), percolation theory, etc. Others 90

Modeling Heterogeneous Wireless Sensor Networks n n Application-specific nature of sensor networks Two main classes (based on applications) ¡ ¡ n Data gathering sensor networks ¡ n Periodic data gathering cycles, correlated measurements, data aggregation Clustering for aggregation and protocol scalability ¡ n Data gathering sensor networks: e. g. environment monitoring, temperature monitoring and control Event detection sensor networks: e. g. forest re detection Hierarchical clustering Guarantee system lifetime 91

Modeling Heterogeneous Wireless Sensor Networks n n n Random deployment of nodes, 2 -D homogeneous Poisson process Each cluster is a Voronoi cell Use simple tools from stochastic geometry to determine the relaying load on critical nodes, P 0 92

Other interesting problems n n n Optimizing a sensor network composed of heterogeneous devices Taking into account layer 3 routing mechanisms when evaluating an ad-hoc or sensor network connectivity Taking into account the MAC layer and radio channel properties when modeling sensor networks Link with graph theory (e. g. small worlds), percolation theory, etc. Others 93

Routing in dense ad-hoc or sensor networks n High number of nodes and high connectivity requires: ¡ ¡ New addressing paradigms New routing approaches New algorithms for multicast and broadcast Etc. 94

Self-organization of the network n n Each node elect the node in its neighborhood with the highest metric. Metric examples : ¡ ¡ Degree of a node : number of neighbors for this node Density of a node : number of edges between neighbors of the node 95

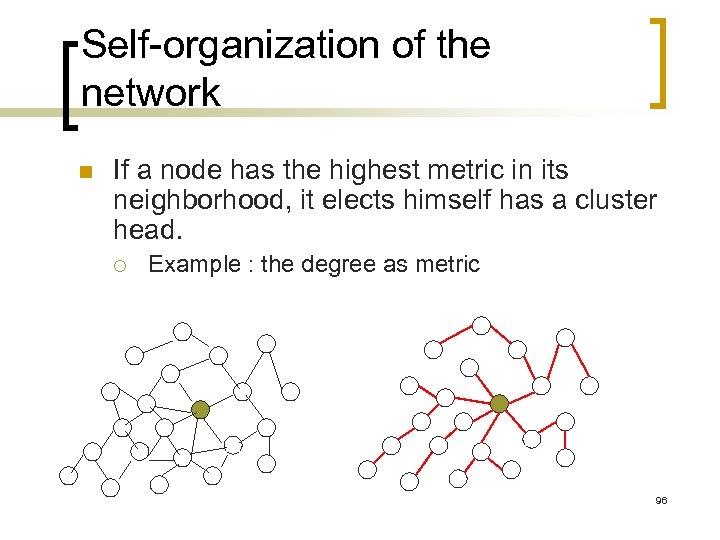Self-organization of the network n If a node has the highest metric in its neighborhood, it elects himself has a cluster head. ¡ Example : the degree as metric 96

Self-organization of the network Simulation in a random geometric graph (in a square of size 1 x 1) 1000 nodes – radius 0. 1 3000 nodes – radius 0. 1 97

Self-organization of the network : results n Geometry sotchastic gives: ¡ ¡ ¡ n Other results are obtained by simulation: ¡ ¡ ¡ n n Bound on the number of clusters, Bound on the probability that a node is a cluster head, Mean and variance of the metrics. Degree of the nodes in the cluster tree Behavior of the cluster when the node are moving (mobile ad-hoc netwkorks) Number of broadcast messages received by the nodes. Mitton, Busson, Fleury, “Self Organization in Large Scale Ad Hoc Networks”, Med. Hoc-Net 2004. Mitton, Fleury, “Self-Organization in Ad Hoc Networks”, reserah report INRIA, RR-5042. 98

Other interesting problems n n n Optimizing a sensor network composed of heterogeneous devices Taking into account layer 3 routing mechanisms when evaluating an ad-hoc or sensor network connectivity Taking into account the MAC layer and radio channel properties when modeling sensor networks Link with graph theory (e. g. small worlds), percolation theory, etc. Others 99

References related with the last cited topics n n n n Vivek Mahtre, Catherine Rosenberg, Daniel Kofman, Ravi Mazumdar, Ness Shroff, A Minimum Cost Surveillance Sensor Network with a Lifetime Constraint, to appear in IEEE Transactions of Mobile Computing (TMC). Sunil Kulkarni, Aravind Iyer, Catherine Rosenberg, Daniel Kofman, Routing Dependent Node Density Requirements for Connectivity in Multi-hop Wireless Networks, accepted, Globecom 2004 Mitton, Busson, Fleury, “Self Organization in Large Scale Ad Hoc Networks”, Med. Hoc-Net 2004. Mitton, Fleury, “Self-Organization in Ad Hoc Networks”, reserah report INRIA, RR-5042. O. Douse, F. Baccelli, P. Thiran, Impact of Interferences on Connectivity in Ad-Hoc Networks, in Proc. IEEE Infocom 2003 O. Douse, P. Thiran and M. Hasler, Connectivity in ad-hoc and hybrid networks”, in Proc. IEEE Infocom, 2002 M. Grossglauser and D. TSe, Mobility increases the capacity of adhoc woireless networks, in Proc. Infocom 2001 100

Content n Introduction ¡ ¡ n A Simple example to illustrate what S. G. is ¡ n n n Application domains in the telecommunication world Why Stochastic Geometry (S. G. )? Network infrastructure optimization Theoretical framework, part 1 – Tessellation processes Other application examples (CDNs, Multicast routing) Theoretical framework, part 2 – Coverage processes More application examples (CDMA, Ad-hoc and sensor networks) Summary: Main mathematical objects, Main known results Conclusions and Perspectives 101

Targeted results of S. G. modeling n n n Modeling complex systems through a reduced number of parameters Capturing Spatial/Geometric Properties A priori evaluation of the cost of a network/system to be deployed, ¡ n Optimization of main parameters ¡ n E. g. Mobile network: before knowing the exact position of each antenna, an estimation of the future cost of the network can be obtained Estimation of the amount of equipment that has to be deployed Not applicable to find the optimal location of system equipment over a deterministic known infrastructure 102

Main tools n Point Processes on the space ¡ n Stochastic Geometry ¡ n E. g. to represent the elements of the network and their variability on time and space To represent how these elements are structured (service zones represented by tessellations, coverage zones, etc. ) Palm theory ¡ To calculate the required performance metrics expressed as functionals of the previous stochastic objects. 103

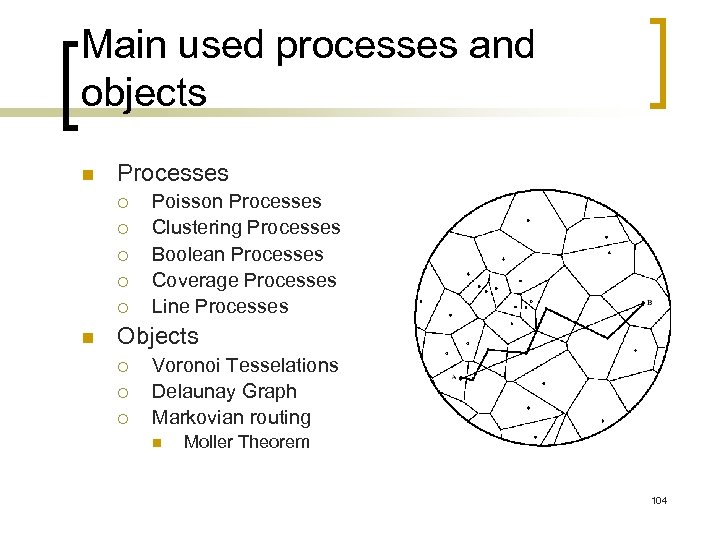Main used processes and objects n Processes ¡ ¡ ¡ n Poisson Processes Clustering Processes Boolean Processes Coverage Processes Line Processes Objects ¡ ¡ ¡ Voronoi Tesselations Delaunay Graph Markovian routing n Moller Theorem 104

Conclusion n Stochastic Geometry is a powerful and useful tool to ¡ ¡ n n n Model spatial properties of big size systems With a reduced number of parameters To evaluate average performance measures and costs And to optimize main parameters The number of applications in the telecommunication world has exploded during the past 3 years The approach has been used by the telecom operators; for example, to estimate the cost of access networks There is an important ongoing work, both on theoretic and applied problems ¡ To consider more sophisticated models n n Hybrid models capturing both time and geometric properties To model the non-homogeneous distribution of equipment To obtain formulae for measures other than « averages » To analyze new type of systems like peer-to-peer architectures, Wi. Fi deployments, sensor networks, etc. 105

Short Bibliography (1) n See http: //www. di. ens. fr/~mistral/sg/ n Books ¡ ¡ ¡ n Poisson Voronoï tesselations [MØLLER] ¡ ¡ n Stoyan, Kendall and Mecke. « Stochastic geometry and its applications. » Ed : Wiley. (main results on point process, palm calculus, boolean model and other models). Okabe, Boots, Sugihara, and Chiu « Spatial tesselations » . Concepts and applications of Voronoï diagrams. Ed : Wiley. Penrose. « Random Geometric graphs » . Ed : Oxford University Press. MØLLER. “Random tesselation in d » . Adv. Appl. Prob. 24. 37 -73. MØLLER. “Lectures on random Voronoï Tesselations. ” Lectures notes in statistics 87. Springer Verlag, New York, Berlin, Heidelberg. Percolation ¡ ¡ ¡ Gupta & Kumar, « Critical power for asymptotic connectivity in wireless networks » , 1998. [Meester 1996] Continuum percolation. Ed : Cambridge University Press. Dousse, Baccelli, Thiran, « Impact of interfernces on connectivity in Ad Hoc Networks » , Infocom 2003. 106

Short Bibliography (2) n SG applied to Network performance evaluation ¡ ¡ ¡ ¡ ¡ F. Baccelli, M. Klein, M. Lebourges, and S. Zuyev. Stochastic geometry and architecture of communication networks. J. Telecommunication Systems, 7: 209227, 1997. Stochastic geometry modelling of hybrid optical networks. (with C. Farinetto) Performance Evaluation 57, 441 -452, 2004. Baccelli, Blaszczyszyn, « On a coverage process ranging from the boolean model to the Poisson voronoï tesselation, with applications to wireless communications » , Adv. Appl. Prob. , vol. 33(2), 2001. Busson, Rougier, Kofman, « Impact of Tree Structure on Retransmission Efficiency for TRACK”. NGC 2001. Busson, Kofman, Rougier, « Optimization of Content Delivery Networks Server Placement”, ITC 18, Berlin. Baccelli, Kofman, Rougier. “Self organizing hierarchical multicast trees and their optimization”. IEEE INFOCOM'99, New York (USA), March 1999. Baccelli, Tchoumatchenko, Zuyev. “Markov paths on the Poisson-Delaunay graph with applications to routing in mobile networks. ” Adv. Appl. Probab. , 32(1): 1 -18, 2000. Baccelli, Gloaguen, Zuyev. “Superposition of planar voronoi tessellations”. Comm. Statist. Stoch. Models, 16(1): 69 -98, 2000. Mitton, Busson, Fleury, “Self Organization in Large Scale Ad Hoc Networks”, Med. Hoc-Net 2004. 107

Short Bibliography (3) n SG applied to Network performance evaluation ¡ ¡ ¡ ¡ ¡ F. Baccelli, B. Blaszczyszyn, and F. Tournois. Spatial averages of coverage characteristics in large CDMA networks. Technical Report 4196, INRIA, June 2001. F. Baccelli and S. Zuyev. Stochastic geometry models of mobile communication networks. In Frontiers in queueing, pages 227 -243. CRC Press, Boca Raton, FL, 1997. Vivek Mahtre, Catherine Rosenberg, Daniel Kofman, Ravi Mazumdar, Ness Shroff, A Minimum Cost Surveillance Sensor Network with a Lifetime Constraint, to appear in IEEE Transactions of Mobile Computing (TMC). Sunil Kulkarni, Aravind Iyer, Catherine Rosenberg, Daniel Kofman, Routing Dependent Node Density Requirements for Connectivity in Multi-hop Wireless Networks, accepted, Globecom 2004 O. Douse, F. Baccelli, P. Thiran, Impact of Interferences on Connectivity in Ad-Hoc Networks, in Proc. IEEE Infocom 2003 O. Douse, P. Thiran and M. Hasler, Connectivity in ad-hoc and hybrid networks”, in Proc. IEEE Infocom, 2002 M. Grossglauser and D. TSe, Mobility increases the capacity of ad-hoc woireless networks, in Proc. Infocom 2001 Mitton, Busson, Fleury, “Self Organization in Large Scale Ad Hoc Networks”, Med. Hoc-Net 2004. Mitton, Fleury, “Self-Organization in Ad Hoc Networks”, reserah report INRIA, RR 5042. 108