Stochastic Games Krishnendu Chatterjee CS 294 Game Theory

Stochastic Games Krishnendu Chatterjee CS 294 Game Theory

Games on Components. n Model interaction between components. n Games as models of interaction. n Repeated Games: Reactive Systems.

Games on Graphs. n Today’s Topic: n n n Games played on game graphs. Possibly for infinite number of rounds. Winning Objectives: n n Reachability. Safety ( the complement of Reachability).

Games. n n 1 Player Game : Graph G=(V, E). R µ V which is the target set. 2 Player Game: G=(V, E, (V , V})). Rµ V. (alternating reachability).

Games. n n 1 Player Game : Graph G=(V, E). R µ V which is the target set. 1 -1/2 Player Game (MDP’s) : G=(V, E, (V , V°)). Rµ V. 2 Player Game: G=(V, E, (V , V})). Rµ V. (alternating reachability). 2 -1/2 Player Game: G=(V, E, (V , V}, V°)). Rµ V.

1 -1/2 player game

Markov Decision Processes. • A Markov Decision Process (MDP) is defined as follows: • G=(V, E, (V , V°) R) • (V, E) is a graph. • (V , V°) is a partition. • Rµ V – set of Target nodes. • V° are random nodes chooses between successors uniformly at random. • For simplicity we assume our graphs are binary.

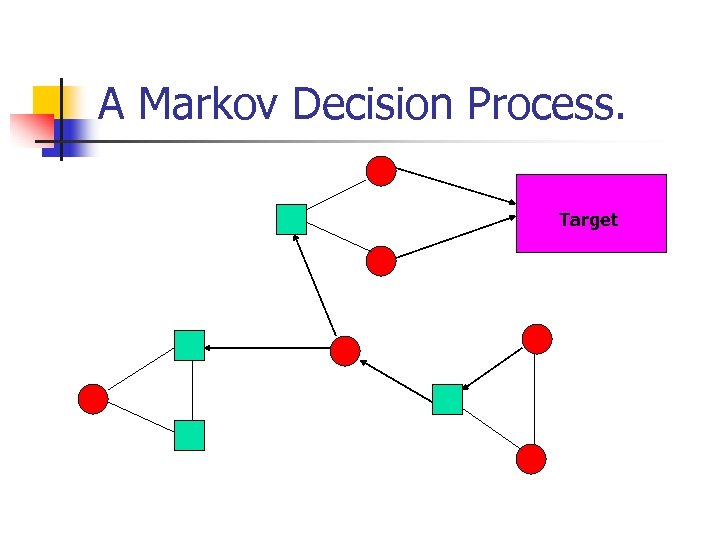A Markov Decision Process. Target

Strategy. n 1: V* ¢ V ! D(V) such that for all x 2 V* and v 2 V , if 1(x ¢ v) >0, (v, 1(x ¢ v) ) 2 E. ( D(V) is a probability distribution over successor).

Subclass of Strategies. n n n Pure Strategy : Chooses one successor and not a distribution. Memoryless Strategy: Strategy independent of the history. Hence can be represented as 1: V ! D(V) Pure Memoryless Strategy is a strategy which is pure and memoryless. Hence can be represented as 1: V ! V

Values. n Reach(R)={ s 0 s 1 … | 9 k. sk 2 R } n v 1(s) =sup 1 2 1 Pr 1( Reach (R) ) n Optimal Strategy: 1 is optimal if v 1(s) = Pr 1 (Reach (R))

Values and Strategies. n n Pure Memoryless Optimal Strategy exist. [CY 98, FV 97] Computed by the following linear program. minimize s x(s) subject to x(s) ¸ x(s’) (s, s’) 2 E and s 2 V x(s) =1/2(x(s’)+x(s’’)) (s, s’), (s’s’’) 2 E and s 2 V° x(s) ¸ 0 x(s)=1 s 2 R

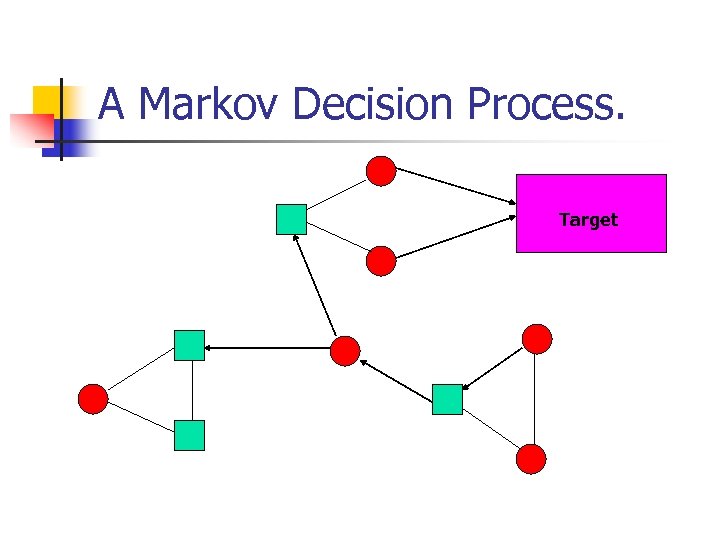A Markov Decision Process. Target

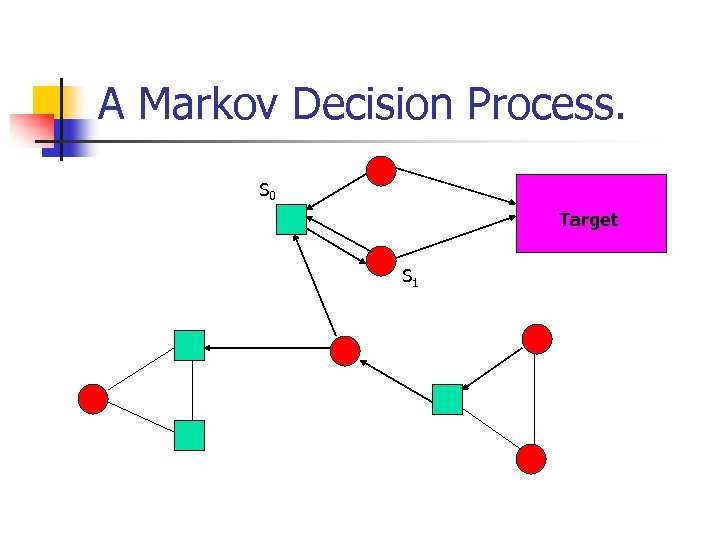A Markov Decision Process. S 0 Target S 1

Pure Memoryless Optimal Strategy. n n n At s 0 the player chose s 1 and at s 1 the play reaches R with probability ½. Hence the probability of not reaching R in n steps is (1/2)n. As n ! 1 this is 0 and hence the player can reach with probability 1.

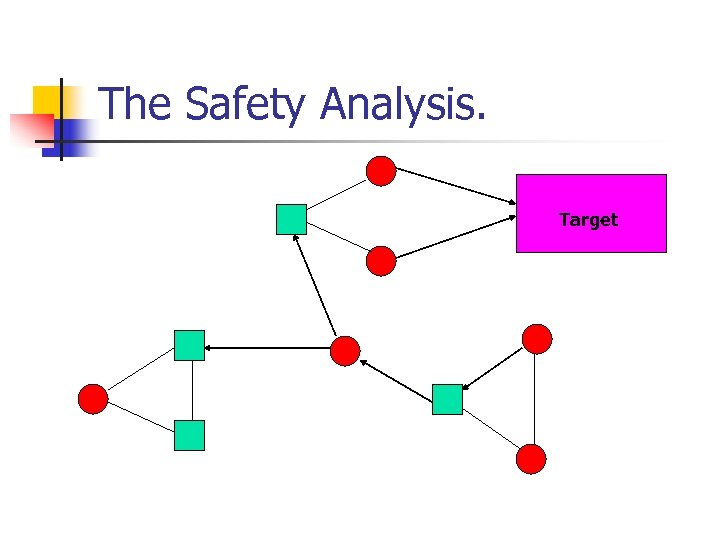The Safety Analysis. Target

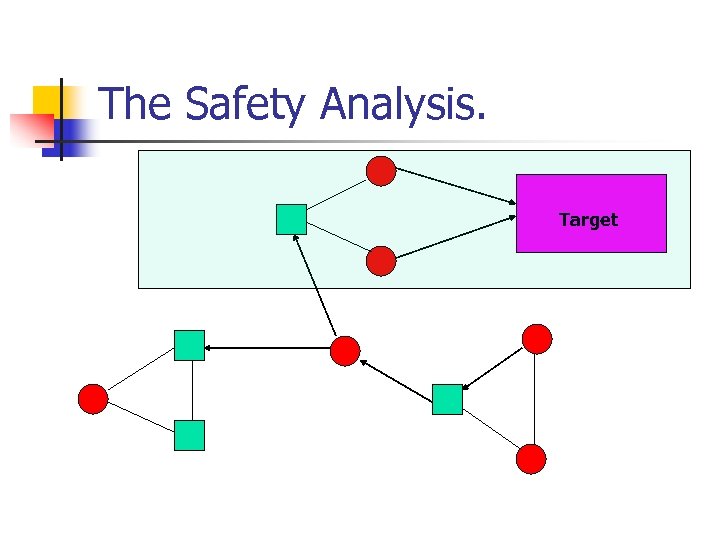The Safety Analysis. Target

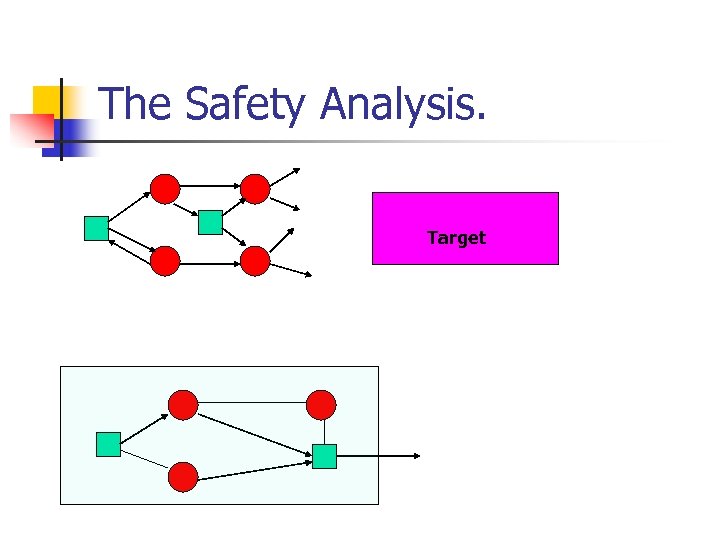The Safety Analysis. Target

The Safety Analysis. n n n Consider the random player as an adversary. Then there is a choice of successors such that the play will reach the target. The probability of the choice of successors is at least (1/2)n.

The Key Fact. n The Fact about the Safety Game: n n n If the MDP is a safety game for the player and it loses with probability 1. The number of nodes is n. Then the probability to reach the target within n steps is at least (1/2)n.

MDP’s. n n n Pure Memoryless Optimal Strategy exists. Values can be computed in polynomial time. The Safety game fact.

2 -1/2 player games

Simple Stochastic Games. n n n G=(V, E, (V , V}, V°)), Rµ V. [Con’ 92] Strategy: i: V* ¢ Vi ! D(V) (as before) Values: v 1(s)= sup 1 inf 2 Pr 1, 2(Reach(R)) v 2(s)=sup 2 inf 1 Pr 1, 2(: Reach(R))

Determinacy. n n n v 1(s) + v 2(s) =1 [Martin’ 98] Strategy 1 for player 1 is optimal if v 1(s) = inf 2 Pr 1, 2(Reach(R)) Our Goal: Pure Memoryless Optimal Strategy.

Pure Memoryless Optimal Strategy. n n n Induction on the number of vertices. Use Pure Memoryless strategy for MDP’s. Also use facts about MDP safety game.

Value Class. n n Value Class is the set of vertices with the same value v 1. Formally, C(p)={ s | v 1(s) =p } We now see some structural property of a value class.

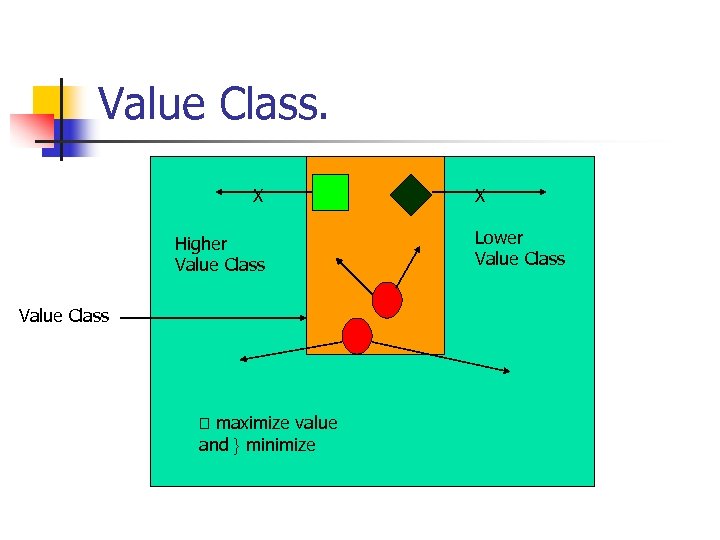Value Class. X Higher Value Class maximize value and } minimize X Lower Value Class

Pure Memoryless Optimal Strategy. n Case 1. There is only 1 value class. n n Case a: R = ; any strategy for player }(2) suffice. Case b: R ; then since in R player (1) wins with probability 1 then the values class must be the value class 1.

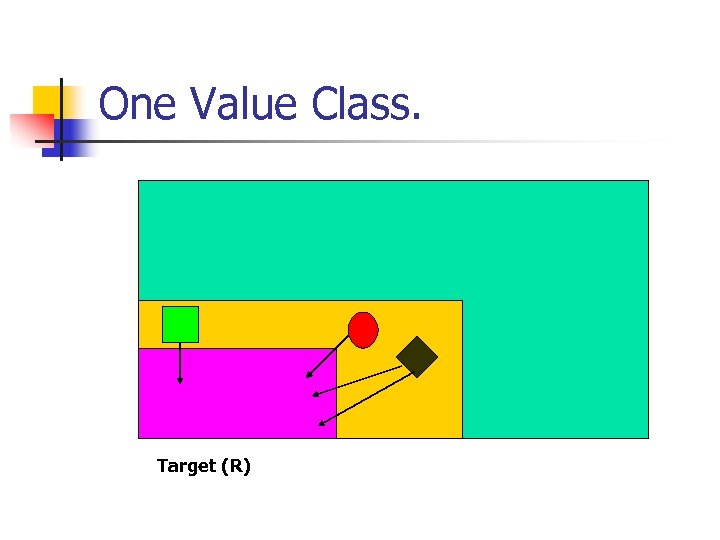One Value Class. Target (R)

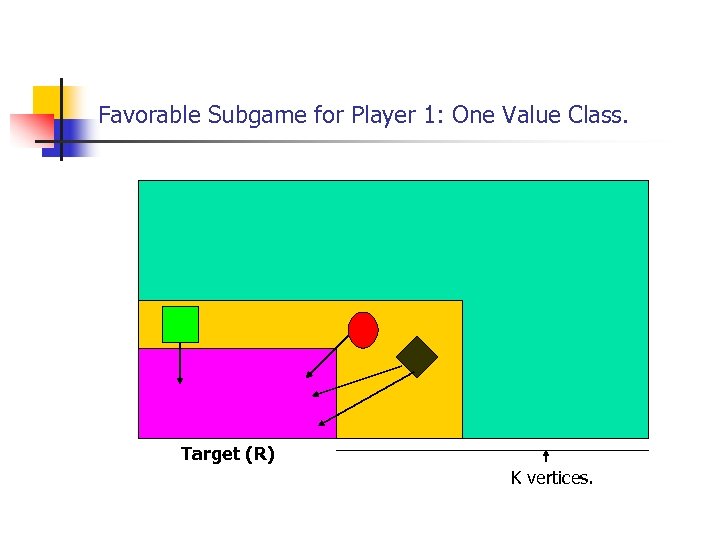Favorable Subgame for Player 1: One Value Class. Target (R) K vertices.

Subgame Pure Memoryless Optimal Strategy. n n n By Induction Hypothesis: pure memoryless optimal strategy in the subgame. Fix the memoryless strategy of the sub-game. Now analyse the MDP safety game. For any strategy of player } (2) the probability to reach the boundaries in k steps is at least (1/2)k.

Pure Memoryless Optimal Strategy. n n The optimal strategy of the subgame ensures that the probability to reach the target in original game in k+1 steps is at least (1/2)k+1. The probability of not reaching the target within (k+1)*n steps is (1 -(1/2)k+1)n which is 0 as n ! 1.

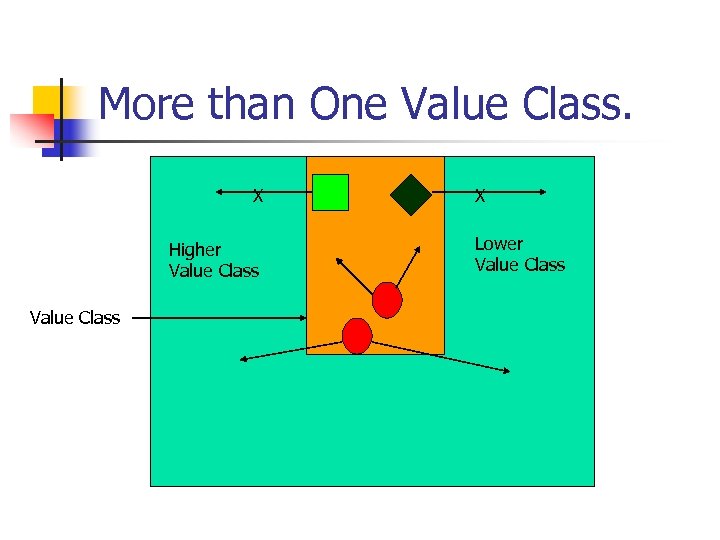More than One Value Class. X Higher Value Class X Lower Value Class

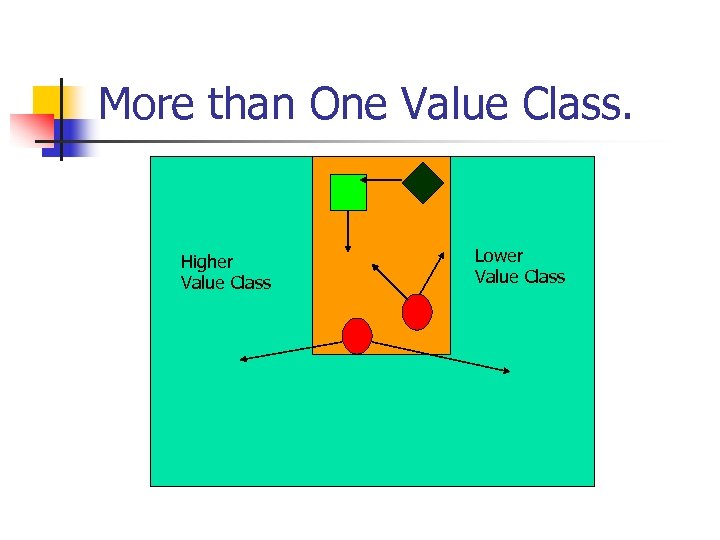More than One Value Class. Higher Value Class Lower Value Class

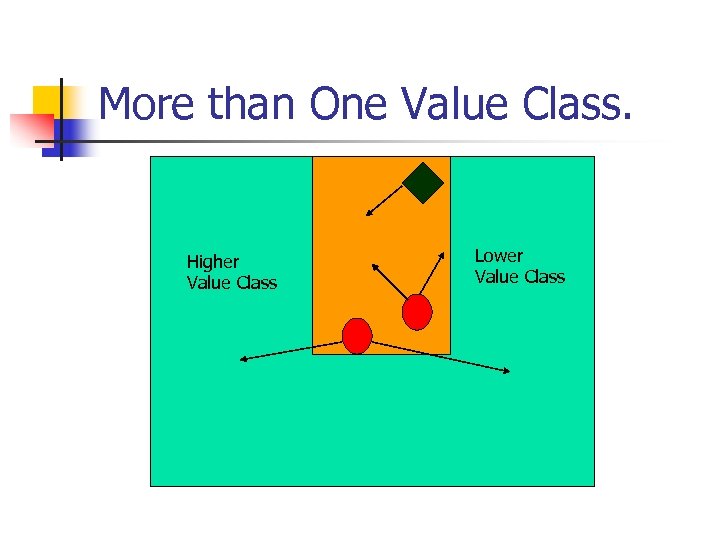More than One Value Class. Higher Value Class Lower Value Class

Pure Memoryless Optimal Strategy. n n Either can collapse a vertex in which case we can apply induction hypothesis. Else in no value class there is a vertex for player 1 (V is empty) n Then it is a MDP and pure memoryless optimal strategy of MDP suffice.

Computing the values. n Given a vertex s and value v’ if v 1(s) ¸ v’ can be achieved in NP Å co. NP. n Follows from pure memoryless optimal strategy and that values of MDP’s can be computed in polytime.

Algorithms for determining values. n Algorithms [Con’ 93] n n Randomized Hoffman-Karp. Non-linear programming. All these algorithms practically efficient. Open problem: Is there a polytime algorithms to compute the values?

Limit Average Games. n n n r: V ! N (zero sum) The payoff is limit average or mean-payoff limn! 1 1/n i=1 to n r(si) Two player mean payoff games can be reduced to Simple Stochastic Reachability Game. [ZP’ 96] Two player Mean payoff games can be solved in NP Å co. NP. Polytime algorithm is still open?

Re-Search Story. n 2 -1/2 Player Limit Average Pure Memoryless Strategy: n n n Gilette’ 57 : Wrong version of the proof. Liggett & Lippman’ 69: New Correct Proof. 2 Player Limit Average Pure Memoryless Strategy n n n Ehrenfeucht & Mycielski ’ 78: “ didn’t understand” Gurvich, Karzanov & Khachiyan ’ 88: “typo” Zwick & Patterson ’ 96 : Quasi polynomial time algorithm Slide Due to Marcin Jurdzinski

N-player games. n Pure Memoryless Optimal Strategy for 2 player zero-sum games can be used to prove existence of Nash Equilibrium in n-player games. n n n Key Idea: Threat Strategy as in Folk Theorem. [TR’ 97] No body has an incentive to change as other will punish. We require pure strategy to detect deviation.

Concurrent Games

Concurrent Games. n n Previously games were turn-based either player or player } chose moves or player ° chose successor randomly. Now we allow the players to play concurrently. G=(S, Moves, 1, 2, ) n n i: S ! 2 Moves n ; : S £ Moves ! S

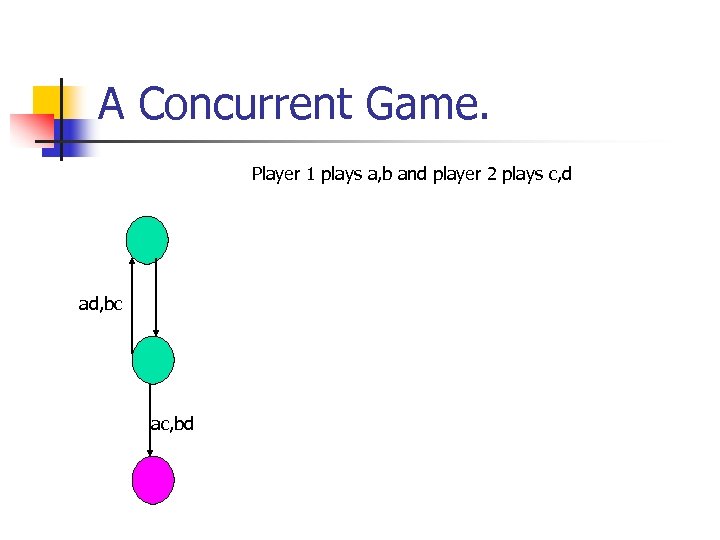A Concurrent Game. Player 1 plays a, b and player 2 plays c, d ad, bc ac, bd

Concurrent games. n n Concurrent Game with Reachability Objective [d. AHK’ 98] Concurrent Game with arbitrary regular winning objective [d. AH’ 00, d. AM’ 01]

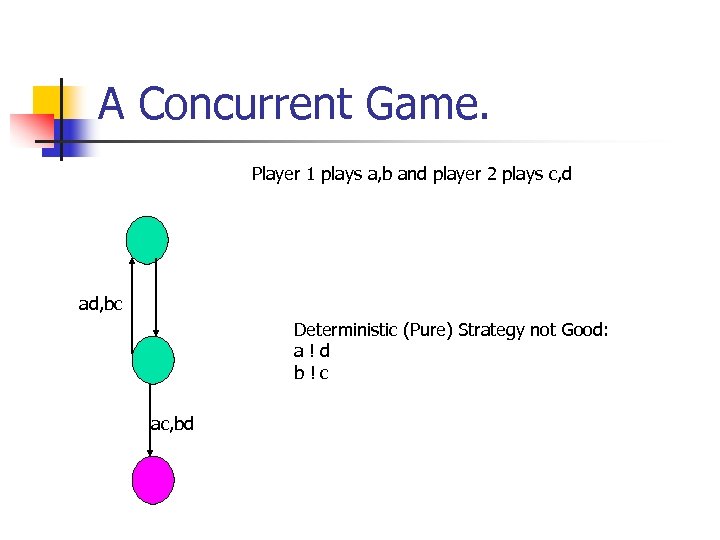A Concurrent Game. Player 1 plays a, b and player 2 plays c, d ad, bc Deterministic (Pure) Strategy not Good: a!d b!c ac, bd

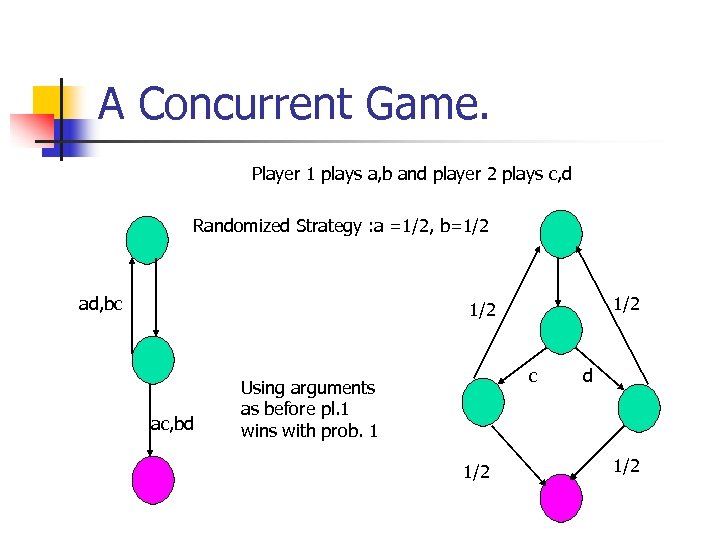A Concurrent Game. Player 1 plays a, b and player 2 plays c, d Randomized Strategy : a =1/2, b=1/2 ad, bc 1/2 ac, bd c Using arguments as before pl. 1 wins with prob. 1 1/2 d 1/2

Concurrent Games and Nash equilibrium. ad ac, bd bc Fact: For any strategy for player 1 he cannot win with prob. 1. As long player 1 plays move “a” deterministically player 2 plays move “d”, when player 1 plays “b” with positive probability then player 2 plays “c” with positive probability. Thus (1, 0) not a Nash Equilibrium.

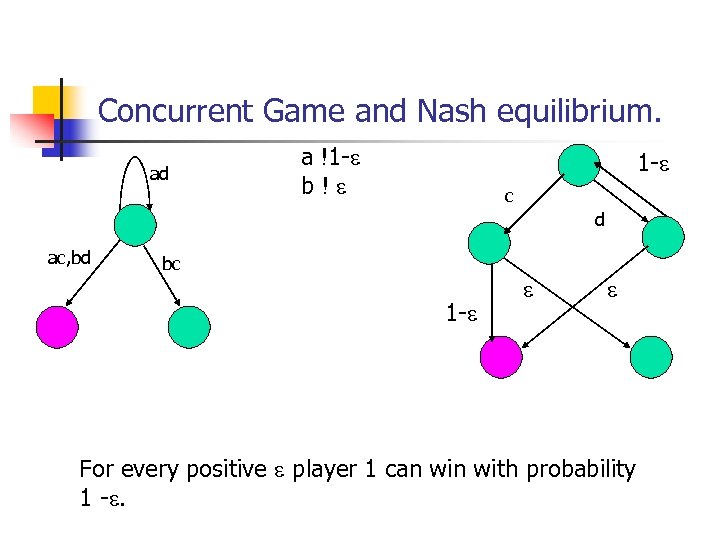Concurrent Game and Nash equilibrium. ad a !1 - b! 1 - c d ac, bd bc 1 - For every positive player 1 can with probability 1 -.

Why is “c” better? n n n If player 2 plays “d” then reaches target with probability . Probability of not reaching target in n steps is (1 - )n and this is 0 as n ! 1. For move “c” player 1 reaches target with probability (1 - )

No Nash Equilibrium. n n We saw earlier that (1, 0) is not a Nash equlibrium. For any positive we have (1 - , ) is not a Nash equilibrium as player 1 can choose a positive ’ < and achieve (1 ’, ’)

Concurrent Game: Borel Winning Condition. n n Nash equilibrium need not necessarily exist but -Nash equilibrium exist for 2 -player concurrent zero-sum games for entire Borel hierarchy. [Martin’ 98] The Big Open Problem: Existence of -Nash equilibrium for nplayer / 2 player non zero-sum games. Safety games: n-person concurrent game Nash equilibrium exist. [Sudderth, Seechi’ 01] Existence of Nash equilibrium and complexity issues for nperson Reachability game. (Research Project for this course)

Concurrent Games: Limit Average Winning Condition. n n The monumental result of [Vieille’ 02] shows -Nash equilibrium exist for 2 player concurrent non-zero sum limit average game. The big open problem: Existence of Nash equilibrium for n-player limit average game.

Relevant Papers. 1. Complexity of Probabilistic Verification : JACM’ 98 – Costas Courcoubetis and Mihalis Yannakakis 2. The Complexity of Simple Stochastic Games: Information and Computatyon’ 92 - Anne Condon 3. On algorithms for Stochastic Games – DIMACS’ 93 Anne Condon 4. Book: Competitive Markov Decision Processes. 1997 J. Filar and K. Vrieze 5. Concurrent Reachability Games : FOCS’ 98 Luca de. Alfaro, Thomas A. Henzinger and Orna Kupferman

Relevant Papers 6. Concurrent - regular Games: LICS’ 00 Luca de. Alfaro and Thomas A Henzinger 7. Quantitative Solution of -regular Games : STOC’ 01 Luca de. Alfaro and Rupak Majumdar 8. Determinacy of Blackwell Games: Journal of Symbolic Logic’ 98 Donald Martin 9. Stay-in-a-set-games : Int. Journal in Game Theory’ 01 S. Seechi and W. Sudderth ’ 01 10. Stochastic Games: A Reduction (I, II): Israel Journal in Mathematics’ 02, N. Vieille 11. The complexity of mean payoff games on graphs: TCS’ 96 U. Zwick and M. S. Patterson ’ 96

Thank You !!! n http: www. cs. berkeley. edu/~c_krish/