Степенная функция с натуральным показателем Функция заданная

Степенная функция с натуральным показателем

Функция, заданная формулой f(x) = xn, где n N, называется степенной функцией с натуральным показателем.

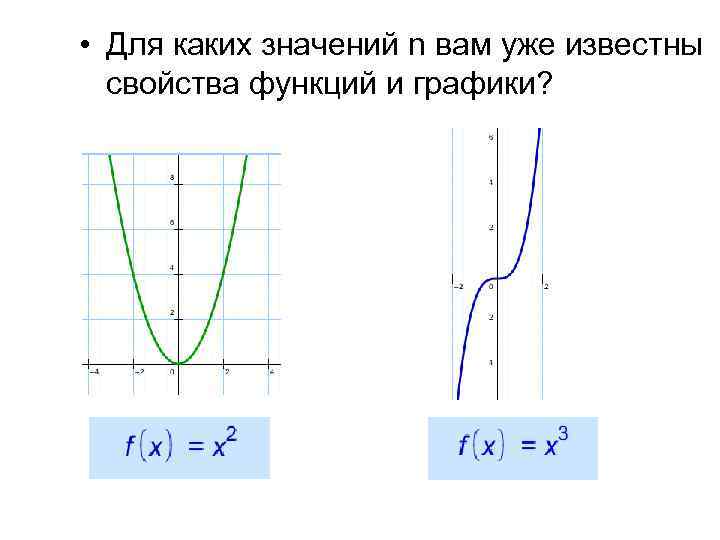• Для каких значений n вам уже известны свойства функций и графики?

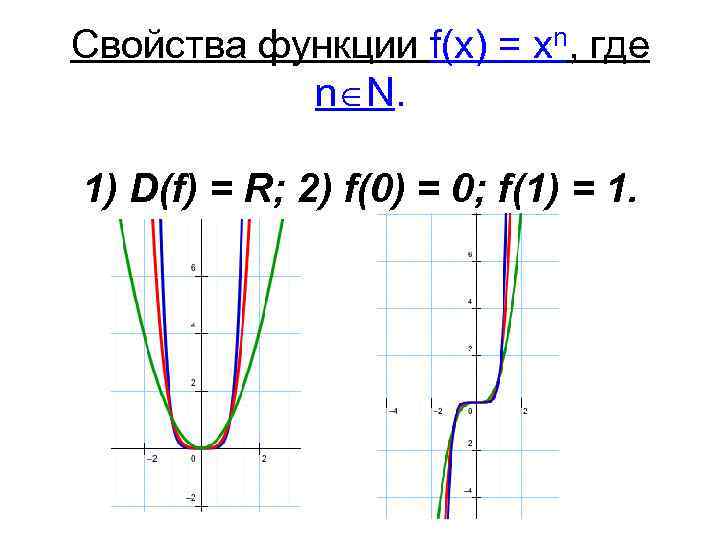Свойства функции f(x) = xn, где n N. 1) D(f) = R; 2) f(0) = 0; f(1) = 1.

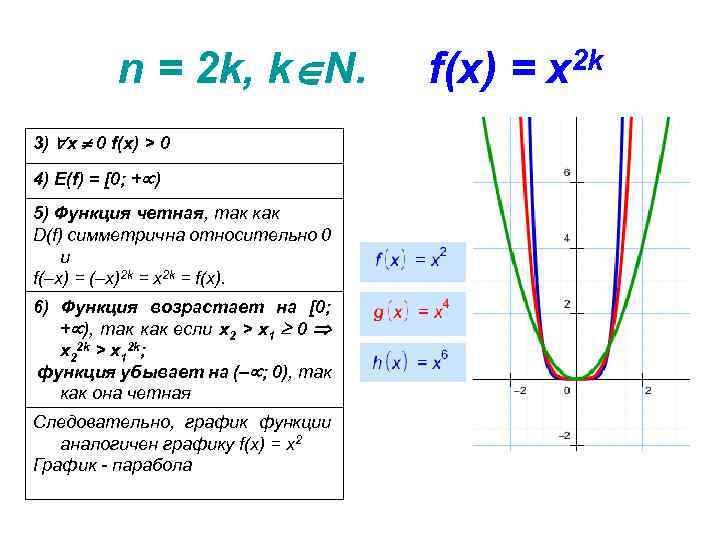n = 2 k, k N. 3) x 0 f(x) > 0 4) E(f) = [0; + ) 5) Функция четная, так как D(f) симметрична относительно 0 и f(–x) = (–x)2 k = x 2 k = f(x). 6) Функция возрастает на [0; + ), так как если x 2 > x 1 0 x 22 k > x 12 k; функция убывает на (– ; 0), так как она четная Следовательно, график функции аналогичен графику f(x) = x 2 График - парабола f(x) = x 2 k

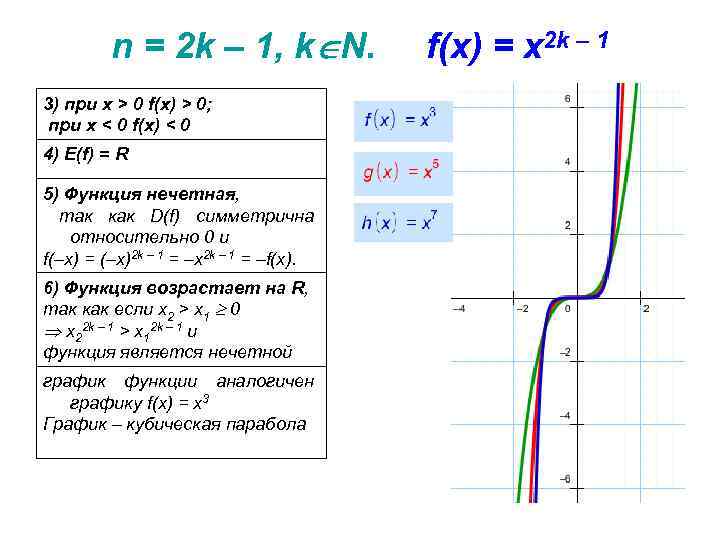n = 2 k – 1, k N. 3) при x > 0 f(x) > 0; при x < 0 f(x) < 0 4) E(f) = R 5) Функция нечетная, так как D(f) симметрична относительно 0 и f(–x) = (–x)2 k – 1 = –x 2 k – 1 = –f(x). 6) Функция возрастает на R, так как если x 2 > x 1 0 x 22 k – 1 > x 12 k – 1 и функция является нечетной график функции аналогичен графику f(x) = x 3 График – кубическая парабола f(x) = x 2 k – 1