Степень с натуральным и целым показателем Степень

Степень с натуральным и целым показателем

Степень с натуральным показателем an= a∙a∙…∙a n Степенью числа a с натуральным показателем n называется произведение n множителей, каждый из которых равен a.

Свойства степени

Определение степени с нулевым показателем Степень числа a, не равного нулю, с нулевым показателем равна единице

-24 1, 674 • 10 В чём смысл этой записи?

Определение степени с целым отрицательным показателем Если а 0 и n , то

2 3 3 = 9 ; 0, 01 =0, 001 = 2 22 4 = 16; ; (-6) == 36 (-6) ° 23 23 5 = 1 ; ; 1 = 1 1 = °° 6 О =0; 0= 1 0=

Представьте число в виде произведения двух одинаковых множителей двумя способами: 25 1/81 1/25 2 1/а

Найдите число, обратное данному: 6 1/7 0 2 а 2 1/х (x≠ 0) 0 2 х 1/6 2 1/а 7

Вписать такие основания и показатели степени, чтобы получились верные равенства 4 -6∙а- =а-2 а a) -3 -2 ∙ a- =a-5 в) a 4 -2 д) (a-) =a-8 a-2 7 б) ∙ a- =a 5 8 г) а- ∙ а-3 = а 5 5 е) 3 -5 ∙ __-5 =15 -5

1. Выполнить действия а-11 a) а-6∙а∙а-4 =___; -4)-2 =___; а 8 в) (a a-8 -5 =___; а-3 a б) : 1 г) а-15: а-15 = ___; -3∙а=___. а-2 е) а д) (2 a 3)-3 =___; 2. Вписать недостающий множитель -5 ∙ ___ 4 а-5 3 а =12 а-10; а) в) 6 а-2 b-4 ∙ 4 а-7 b=24 а-9 b-3; ____ 4 a 8 =32 а 2; б) ___ -2 a-5 b 8 г) _____∙(-3 а 4 b-2)=6 а-1 b 6. (2 а-2)3 ∙

Представьте выражение в виде степени

Упростите

Представьте выражение x-12 в виде произведения двух степеней с основанием x, если один множитель известен. X-12 x-2 x 14 x-18 x 5 x

Вычислите

Расположите в порядке убывания 0, 2 -6; 0, 20; 0, 2; (0, 2)-4; 0, 23

При каких значениях х верно равенство

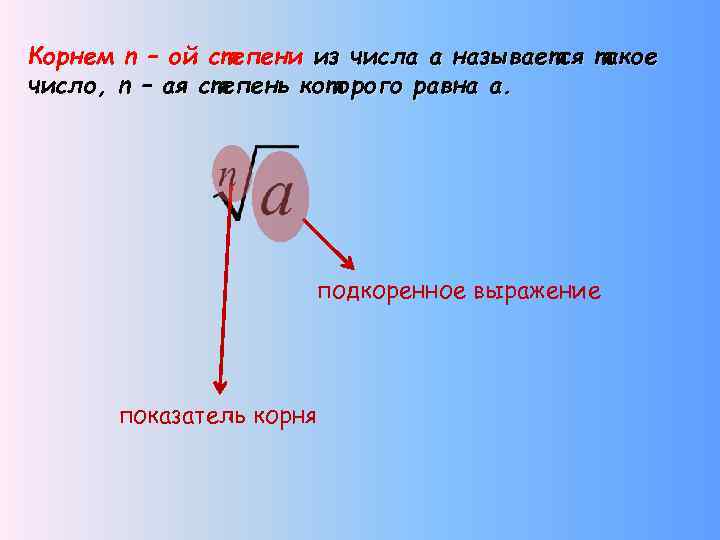Корнем n – ой степени из числа а называется такое число, n – ая степень которого равна а. подкоренное выражение показатель корня

Корень нечетной степени из отрицательного числа можно выразить через арифметический корень.

Свойства корней

Покажем на примерах, как используются свойства корней и рациональных степеней в вычислениях. • Пример 1. Вычислить

Решение. 1) Упростим сначала первую часть выражения. Используя свойство , получим. Теперь применим свойства и : Применим теперь свойство : В итоге мы получили: 2) По свойству : Подставим результаты вычислений из 1) и 2) в выражение Здесь мы использовали свойства и арифметических корней. Ответ: 2.

Степень с рациональным показателем

Степень с основанием, равным нулю, определяется только для положительного дробного показателя:

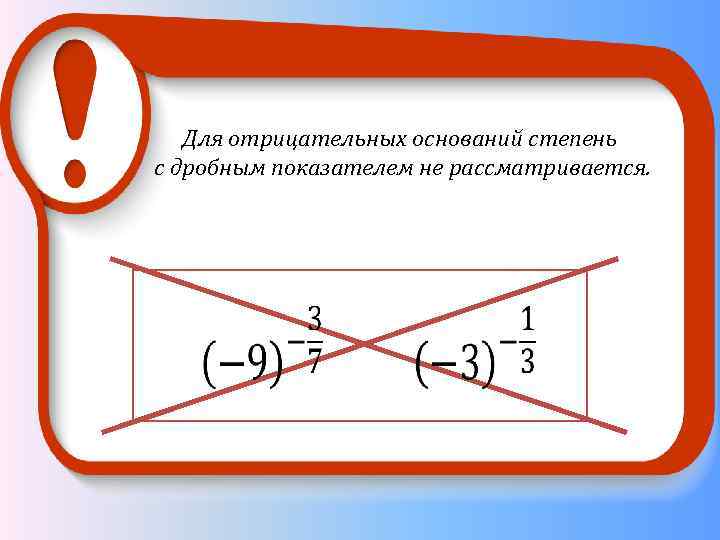Для отрицательных оснований степень с дробным показателем не рассматривается.

Свойства степени с целым показателем справедливы и для степени с любым рациональным показателем.

Решение: • Упростим выражение: Ответ: 50.

Решение: • Разложим на множители числитель и знаменатель дроби: