Ферми,Бозе.pptx
- Количество слайдов: 25

Статистики Ферми - Дирака и Бозе - Эйнштейна Никольский А. В. 2013

Введение Согласно современной квантовой теории все элементарные частицы разделяются на два класса. К первому классу относятся электроны, протоны, нейтроны и все частицы с так называемым полуцелым спином. Эти частицы подчиняются статистике Ферми-Дирака. Они называются фермионами.

Введение Ко второму классу относятся фотоны, π- и Kмезоны и все частицы с целочисленным спином. Эти частицы называются бозонами. Никаких других возможностей квантовая теория не допускает. Статистика Больцмана является приближенным предельным случаем, в который переходят при определенных условиях статистики Ферми. Дирака и Бозе-Эйнштейна.

Введение Во всех трех статистиках допустимые микросостояния принимаются равновероятными. Но статистики отличаются друг от друга тем, как они определяют микросостояния и статистические веса макросостояний.

Введение Статистика Больцмана стоит на точке зрения принципиальной различимости частиц, даже когда частицы абсолютно тождественны. Квантовые статистики Ферми-Дирака и Бозе-Эйнштейна, наоборот, стоят на точке зрения принципиальной неразличимости тождественных частиц.

Введение Различие: в статистке Ферми-Дирака принимается, что в каждом квантовом состоянии может находиться не более одной частицы. Статистика Бозе-Эйнштейна подобных ограничений не накладывает. Она допускает, что в каждом квантовом состоянии может находиться любое число частиц. Столь различное поведение бозонов и фермионов обосновывается в квантовой механике теории поля.

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Мы имеем в виду идеальный газ, состоящий из фермионов и бозонов, помещенный в сосуде неизменного объема с твердыми, непроницаемыми адиабатическими стенками. Чтобы охарактеризовать макросостояние газа, разделим все квантовые состояния частицы на узкие энергетические слои.

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Каждый слой состоит из квантовых состояний с одинаковыми или очень близкими значениями энергии частицы. Энергии квантовых состояний в i-м слое заключены в интервале. При чем. Кроме того, число квантовых состояний в энергетическом слое должно быть очень велико. Макросостояние газа характеризуется заданием числа частиц в каждом энергетическом слое.

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Понятно, что любая перестановка частиц в слое не меняет ни микро-, ни макросостояние. Определим теперь число микросостояний, с помощью которых может быть осуществлено рассматриваемое макросостояние газа с фиксированными числами , т. е. статистический вес G этого макросостояния.

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Число способов, которыми можно распределить частиц по квантовым состояниям i-го слоя, будет: или Для фермионов и бозонов соответственно. Перемножая все , найдем статистический вес рассматриваемого макростостояния всего газа.

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Таким образом, для фермионов: , (1) а для бозонов: . (2)

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Задача состоит в том, чтобы найти наиболее вероятные распределения, обращающие в максимум выражения (1) и (2) при дополнительных условиях: (3). (4)

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Первое из них выражает постоянство числа частиц в системе, второе – постоянство ее полной энергии. Только микросостояния, удовлетворяющие этим условиям, являются допустимыми, и только они должны приниматься во внимание. Все прочие микросостояния являются невозможными.

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Предполагая, что велики не только , но и все , применим формулу Стирлинга, откуда найдем энтропию газа из фермионов и бозонов: (5) (6)

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Из условия максимума с учетом (3) получаем: (для фермионов), (для бозонов).

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Из этих выражений следует: (для фермионов), (для бозонов). (7) (8)

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Причем в последней формуле мы пренебрегли еденицей по сравнению с Постоянная - множитель Лагранжа, не зависящий от всех переменных. Черта над поставлена для того, чтобы подчеркнуть, что речь идет о средних значениях , точнее об их значениях в наиболее вероятном состоянии.

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Среднее число частиц , приходящееся на одно квантовое состояние, равно , т. е. (для фермионов), (9) (для бозонов). (10)

Вывод распределений Ферми-Дирака и Бозе-Эйнштейна Здесь введен новый параметр μ, связанный с A соотношением. Это и есть распределения Ферми – Дирака и Бозе – Эйнштейна.
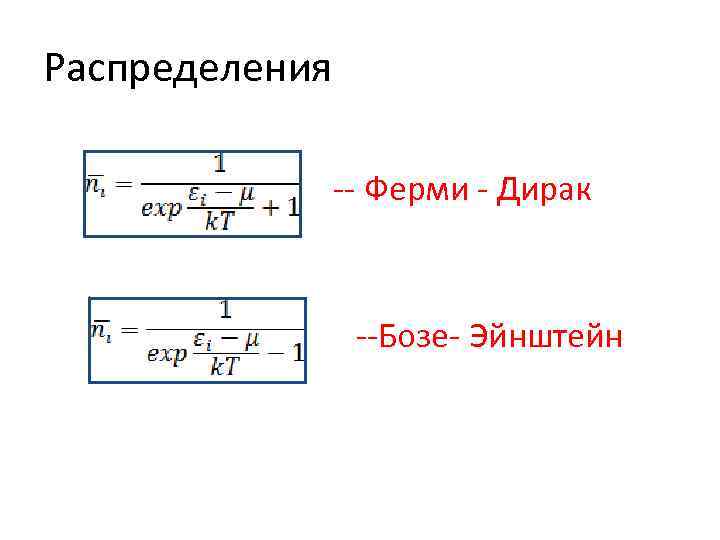
Распределения -- Ферми - Дирак --Бозе- Эйнштейн

Сравнение распределений Больцмана, Ф-Д, Б-Э Если , то в знаменателях формул (9) и (10) можно пренебречь единицами, тогда эти формулы переходят в (11) т. е. в формулу распределения Больцмана. Значит, распределением Больцмана можно пользоваться лишь тогда, когда малы «числа заполения» квантовых ячеек, т. е. при условии.

Сравнение распределений Больцмана, Ф-Д, Б-Э Переход статистик Ферми-Дирака и Бозе - Эйнштейна в статистику Больцмана надо понимать в том смысле, что при выполнении условия формулы (9) и (10) переходят в больцмановскую формулу (11). При этом статистические веса (1) и (2) остаются такими же.
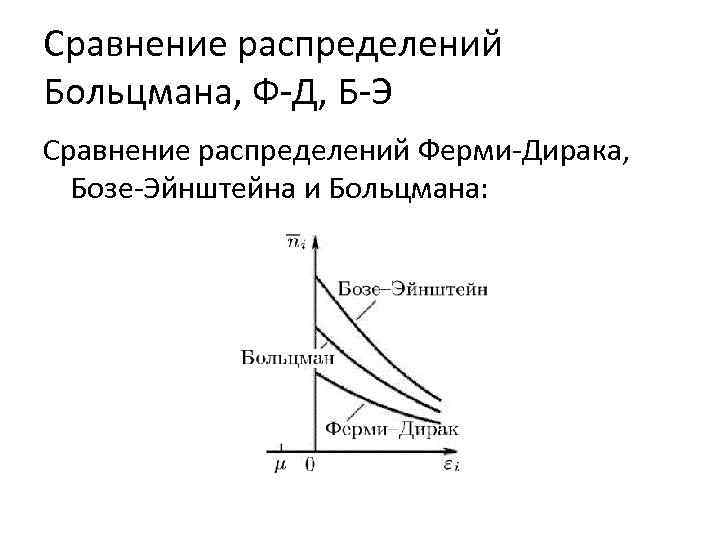
Сравнение распределений Больцмана, Ф-Д, Б-Э Сравнение распределений Ферми-Дирака, Бозе-Эйнштейна и Больцмана:

Однако реальный смысл играют не сами статистические веса, а их логарифмы, точнее, разности логарифмов статистических весов в различных состояниях, определяющие соответствующие приращения энтропии.

Конец фильма
Ферми,Бозе.pptx