Статистикалық жорамалдарды тексеру теориясының негіздері Дәріс жоспары

Статистикалық жорамалдарды тексеру теориясының негіздері.

Дәріс жоспары: 1. Медициналық-биологиялық зерттеулердегі статистикалық жорамалдар. 2. Параметрлік критерийлер. 3. Параметрлік емес критерийлер және олардың қолданылуы. 4. Пирсонның Хи-квадрат, Колмогоров - Смирновтың сәйкестік критерийлері.

Таңдама деректері бойынша бас жиынтықтың параметрлері және қасиеттері жөнінде айтылған ұйғарым статистикалық жорамал деп аталады. Айтылған ұйғарымды (жорамалды) таңдама деректерімен салыстыру үрдісі статистикалық жорамалды тексеру деп аталады. Жорамалдарды статистикалық тексеру міндеттері: §Қандай да бір бас жиынтыққа қатысты Н 0 жорамалы айтылады. §Осы бас жиынтықтан таңдама бөлініп алынады. §Таңдама деректері бойынша Н 0 жорамалын қабылдауға немесе жоққа шығаруға болатындай ереже көрсетілуі тиіс.

Статистикалық жорамал – бұл таралудың түрі жөніндегі немесе бас жиынтықтың белгісіз параметрлерінің шамалары жөніндегі, таңдама көрсеткіштерінің негізінде тексеруге болатын ұйғарым. Статистикалық жорамалдардың мысалдары: Бас жиынтық Гаусстың қалыпты заңы бойынша таралған. Қалыпты таралған екі жиынтықтың дисперсиялары өзара тең.

Статистикалық критерийлер Параметрлік емес

Параметрлік критерийлер деп есептеу формуласына таңдаманың орта мәні, дисперсиясы сияқты параметрлері кіретін және бас жиынтықтың қалыпты таралуына негізделген критерийлерді айтады. Параметрлік емес критерийлер деп бас жиынтықтың таралу түріне негізделмеген және есептеу формуласында жиынтықтың параметрлерін қолданбайтын критерийлерді айтады.

Н 0 нөлдік жорамал деп тексерілуге жататын негізгі жорамалды айтады. Н 1 балама жорамалы деп нөлдік жорамалмен бәсекелес, яғни оған қарама-қайшы келетін жорамалды айтады. Тек бір ғана пікірден тұратын жорамалды жай жорамал деп атайды. Жай жорамалдардың шексіз көп санынан тұратын жорамалды күрделі деп атайды. Н 0 жорамалын тексерудің статистикалық критерийі деп, осы жорамалды қабылдайтын немесе жоққа шығаратын ережені айтады.

Жорамалды принципі тексерудің негізгі Жорамалды тексеру X 1, X 2, …, Xn таңдамасының нәтижелері бойынша жүргізіледі, таңдамадан статистикалық критерий деп аталатын Tn=T(X 1, X 2, …, Xn ) таңдама функциясы құрылады. Tn=T(X 1, X 2, …, Xn ) Сыни аймақ S жорамалды қабылдау аймағы

Жорамалдарды тексергенде мүмкін болатын қателіктер Бірінші текті Екінші текті Н 0 жорамалы Дұрыс емес Жоққа Қабылданады шығарылады 1 -ші текті қателік Қателік жоқ 2 -ші текті қателік

Критерийдің мәнділік деңгейі ( ) деп 1 -ші текті қателікті жіберу ықтималдығын айтады. 2 -ші текті қателіктің ықтималдығы β арқылы белгіленеді. Критерийдің қуаттылығы деп 2 -ші текті қателікті жібермеу ықтималдығын айтады және оны (1 - β) арқылы белгілейді. Р(жоққа шығару Н 0/Н 0 дұрыс) немесе Р(Н 1/Н 0) β Р(қабылдау Н 0/Н 0 дұрыс емес) немесе β Р(Н 0 /Н 1) 1 -β Р(қабылдау Н 1/Н 1 дұрыс) Критерийдің қуаттылығы неғұрлым үлкен болса, соғұрлым 2 -ші текті қатенің ықтималдығы аз.

Жорамалдарды тексеру әдісі: 1. X 1, X 2, …, Xn таңдамасына байланысты Н 0 нөлдік және Н 1 балама жорамалдарды ұйғару. 2. Tn=T(X 1, X 2, …, Xn ) статистикалық критерийін таңдау. (әдетте: U- қалыпты таралу, Х 2 - таралу (Пирсонның хиквадраты), Стьюденттің t- таралуы, Фишердің F-таралуы). 3. Tn статистикалық критерийі және мәнділік деңгейі бойынша tсыни нүктесін , яғни S аймағын аймағынан бөліп тұратын шекараны анықтайды. 4. Х=(X 1, X 2, …, Xn ) таңдамасының сипаттамалары бойынша критерийдің мәндерін есептейді, яғни Tбақ=T(X 1, X 2, …, Xn ) t 5. Егер t S (мысалы, S оң жақтағы аймақ үшін t> tсыни. ), онда Н 0 нөлдік жорамалды жоққа шығарады; ал егер t (t <tсыни), онда Н 0 жорамалын жоққа шығаруға негіз жоқ.

Стьюденттің t-критерийі: Жалпы түрі:

Тәуелсіз таңдамалар жағдайы n 1=n 2=n df=n-1 n 1≠n 2 df= n 1+n 2 -2

Тәуелді таңдамалар жағдайы df=n-1

Қорытынды: Стьюдент критерийі орта мәндердің айырмашылықтары жөніндегі жорамалды тексеру үшін тек қана екі топ үшін қолданылады. • Стьюдент критерийі таңдама көлемі аз болған жағдайда қолданылады, ал бұл медициналықбиологиялық тәжірибелерге тән. • Егер тәжірибе саны көп топтар үшін жүргізілетін болса, онда дисперсиялық талдау әдісі қолданылады. • Стьюдент критерийі қалыпты таралған таңдамалар үшін ғана қолданылады. •

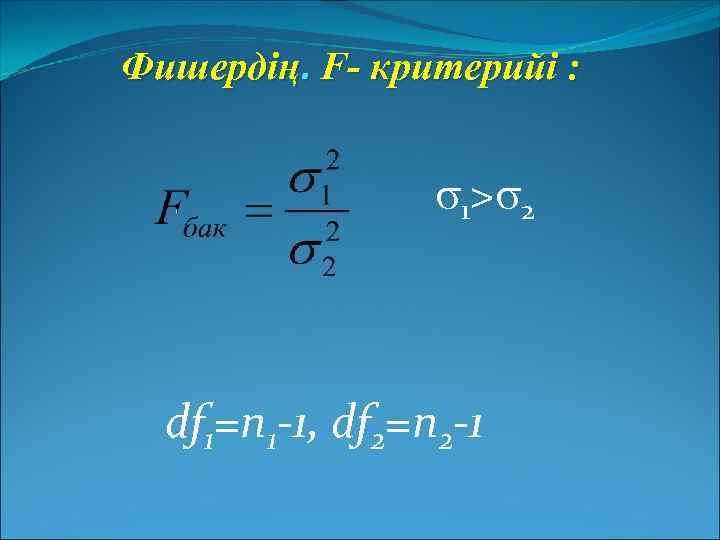
Фишердің. F- критерийі : 1> 2 df 1=n 1 -1, df 2=n 2 -1

Бас жиынтықтың таралу түрі жөніндегі ұйғарымға негізделмеген және осы жиынтықтың параметрлерін қолданбайтын айырмашылық критерийлері параметрлік емес критерийлер деп аталады. Параметрлік емес критерийлердің есептеу формуласында жиіліктер немесе рангілер қолданылады. Параметрлік емес критерийлерді қолдану маңызды: • шолу жасау кезеңінде; • бақылау саны аз (30 – ға дейін); • деректердің қалыпты таралу заңына сәйкестігі белгісіз.

Параметрлік емес критерийлер : • тәуелсіз таңдамалардың топтары арасындағы айырмашылық критерийі; • тәуелді таңдамалардың топтары арасындағы айырмашылық критерийі; негізгі топтарға бөлінеді.

Тәуелсіз топтар арасындағы айырмашылықтар • Тәуелсіз топтар үшін Манна – Уитнидің U критерийі. • Колмогоров – Смирновтың екітаңдамалы критерийі. .

Тәуелді топтар арасындағы айырмашылықтар • таңбалардың z – критерийі; • Уилкоксоннің жұптасқан Т – критерийі;

Ранжирлеу – вариациялық қатардың ішіндегі варианталардың кіші шамадан үлкен шамаға қарай таралуы. Ранжирлеу ережесі: • Кіші мәнге кіші ранг беріледі. • Егер бірнеше мәндер тең болса , оларға олар тең болмаған жағдайда берілетін рангтардың орта мәні болатын ранг беріледі. • Рангтердің жалпы қосындысы есептеу формуласымен сәйкес келуі керек: , мұндағы N- ранжирленетін мәндердің жалпы саны.

Таралудың түрі жөніндегі жорамалды тексеру: Егер зерттелетін кездейсоқ шаманың таралу заңы белгісіз, бірақ оның белгілі бір түрі жөнінде ұйғаруға негіз бар болсын делік (мысалы, оның таралу түрі А болсын). Н 0 - бас жиынтық А заңы бойынша таралған, Н 1 – негізгі жорамал орындалмайды. Хі ni Х 1 n 1 Х 2 n 2 . . . … Хк nk қорытынды: бақылау нәтижесі айтылған ұйғарыммен сәйкес келе ме?

Келісім критерийлері: Келісім критерийі деп белгісіз таралудың түрі жөнінде ұйғарылған жорамалды тексеретін статистикалық критерийді айтады. üПирсонның (Хи-квадрат), üКолмогоров, üФишер, üСмирнов.

Әдебиет: Медик В. А. , Токмачев М. С. , Фишман Б. Б. Статистика в медицине и биологии. М. : Медицина, 2000. • Лукьянова Е. А. Медицинская статистика. - М. : Изд. РУДН, 2002. • Рокицкий П. Ф. Биологическая статистика. Высшая школа, 1973. • И. В. Павлушков и др. Основы высшей математики и математической статистики. (учебник для медицинских и фармацевтических вузов) М. , «ГЭОТАР - МЕД» ; 2003 •

НАЗАРЛАРЫҢЫЗҒА РАХМЕТ