Статистика Тема 4 Cтатистические показатели и средние 1

Статистика Тема 4. Cтатистические показатели и средние 1. Статистические показатели 2. Средние 3. Экскурс: математическое ожидание Dr. Igor Arzhenovskiy

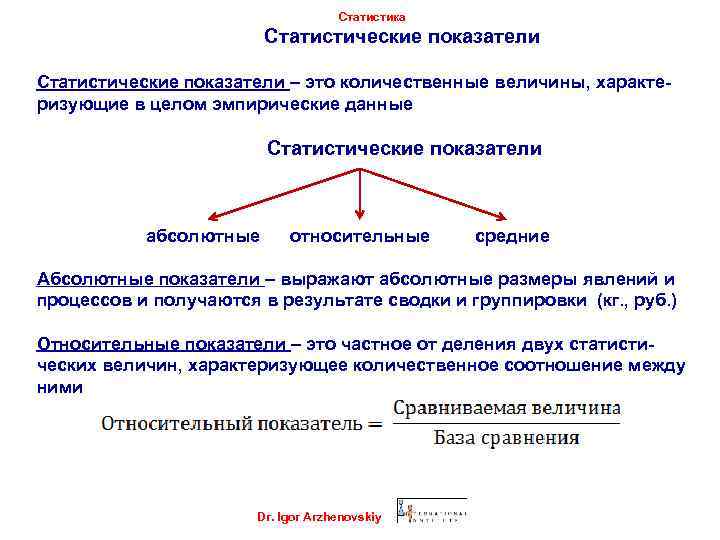Статистика Статистические показатели – это количественные величины, характеризующие в целом эмпирические данные Статистические показатели абсолютные относительные средние Абсолютные показатели – выражают абсолютные размеры явлений и процессов и получаются в результате сводки и группировки (кг. , руб. ) Относительные показатели – это частное от деления двух статистических величин, характеризующее количественное соотношение между ними Dr. Igor Arzhenovskiy

Статистика Виды относительных показателей 1) Выполнения договорных обязательств: 2) Структуры: 3) Сравнения 4) Координации 5) Интенсивности 6) Динамики Dr. Igor Arzhenovskiy

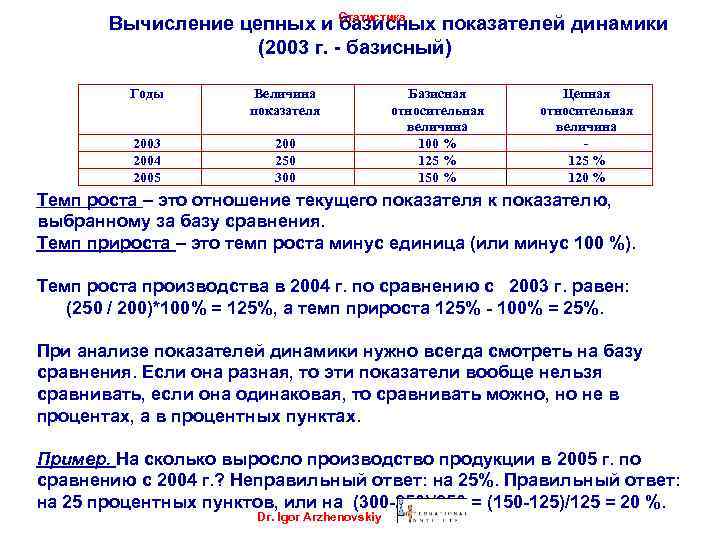Вычисление цепных и Статистика базисных показателей динамики (2003 г. - базисный) Годы Величина показателя 2003 2004 2005 200 250 300 Базисная относительная величина 100 % 125 % 150 % Цепная относительная величина 125 % 120 % Темп роста – это отношение текущего показателя к показателю, выбранному за базу сравнения. Темп прироста – это темп роста минус единица (или минус 100 %). Темп роста производства в 2004 г. по сравнению с 2003 г. равен: (250 / 200)*100% = 125%, а темп прироста 125% - 100% = 25%. При анализе показателей динамики нужно всегда смотреть на базу сравнения. Если она разная, то эти показатели вообще нельзя сравнивать, если она одинаковая, то сравнивать можно, но не в процентах, а в процентных пунктах. Пример. На сколько выросло производство продукции в 2005 г. по сравнению с 2004 г. ? Неправильный ответ: на 25%. Правильный ответ: на 25 процентных пунктов, или на (300 -250)/250 = (150 -125)/125 = 20 %. Dr. Igor Arzhenovskiy

Статистика Средние – это обобщающие показатели, отражающие наиболее типичный уровень варьирующего признака качественно однородных единиц совокупности. Выделяют степенные средние и структурные средние. Макет формулы степенной средней: простая взвешенная Dr. Igor Arzhenovskiy

Статистика Средняя арифметическая простая используется тогда, когда значение признака относится к отдельным единицам наблюдения или к равновеликим группам единиц. Заработная плата по цехам предприятия Цеха (в каждом цехе по работников) Цех 1 Цех 2 Цех 3 100 Dr. Igor Arzhenovskiy Заработная плата по цеху (в у. е. ) 150 200 250

Статистика Средняя арифметическая взвешенная применяется тогда, когда отдельные значения признака встречаются с разной частотой или когда группы не являются равновеликими. Цех 1 2 3 Заработная плата по цехам предприятия Заработная плата по цеху (в Количество работающих в цехе (чел. ) у. е. ) 150 50 200 100 250 150 Dr. Igor Arzhenovskiy

Статистика Средняя гармоническая применяется, если веса равны произведению значения признака на его частоту Заработная плата по цехам предприятия Цех 1 2 Заработная плата по цеху (в у. е. ) 100 200 Dr. Igor Arzhenovskiy Фонд заработной платы (руб. ) 5000 30000

Статистика Средняя геометрическая применяется, если значения признака связаны между собой операциями умножения/ деления, а не сложения/ вычитания Темп роста объёма сбыта по фирме N Годы 2006 2007 2008 2009 Темпы роста, % 103 105 104 106 Среднегодовой темп роста: Среднегодовой темп прироста: 1, 045 – 1= 0, 045 или 4, 5 % Dr. Igor Arzhenovskiy

Статистика Средняя геометрическая Среднегодовой темп роста и прироста можно получить, исходя и из абсолютных значений признака Объём оказанных услуг по фирме N Годы Темпы роста, % 2005 1800 2006 1854 (1854 : 1800 = 1, 03) 2007 1947 2008 2025 2009 2147 Среднегодовой темп роста: Среднегодовой темп прироста: 1, 045 – 1= 0, 045 или 4, 5 %. Dr. Igor Arzhenovskiy

Статистика Другие степенные средние Средняя квадратическая простая и взвешенная: Средняя кубическая простая и взвешенная: Правило мажорантности средних: Dr. Igor Arzhenovskiy

Статистика Свойства средней арифметической ∑ ∑ Dr. Igor Arzhenovskiy

Статистика Структурные средние Мода – наиболее часто встречающееся значение признака Медиана – значение признака у серединной единицы ранжированного ряда Квартили – значения признаков, разбивающие ряд на 4 равные части по 25 % в каждой; второй квартиль является медианой Децили – значения признаков, разбивающие ряд на 10 равных частей Перцентили – значения признаков, делящие ряд на 100 равных частей Средняя арифметическая, мода и медиана при нормальном (а) и умеренно деформированном (б) распределении Dr. Igor Arzhenovskiy

Статистика Расчет моды и медианы в дискретном ряду (несгруппированные данные) При нечетном числе единиц: ранжированный ряд 10 20 20 25 30 Мо = 20 Ме = 20 При четном числе единиц: ранжированный ряд Мо = 20 Ме = (20+25)/2 = 22, 5 Dr. Igor Arzhenovskiy 10 20 20 25 30 35

Статистика Расчет средней арифметической, моды и медианы по данным интервального ряда (сгруппированные данные) Производительность труда на предприятии Производительность труда, изделий в час Xi 0 -10 10 -20 20 -30 30 -40 40 -50 Число работников fi Накопленная частота - F 10 30 25 20 15 10 40 65 85 100 Dr. Igor Arzhenovskiy

Статистика Тема 5. Показатели вариации 1. Понятие вариации 2. Показатели вариации 3. Свойства нормального распределения 4. Моменты Dr. Igor Arzhenovskiy

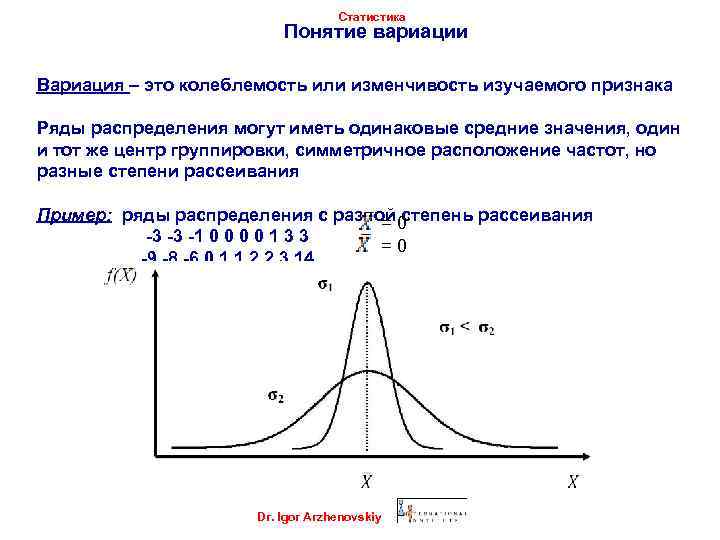Статистика Понятие вариации Вариация – это колеблемость или изменчивость изучаемого признака Ряды распределения могут иметь одинаковые средние значения, один и тот же центр группировки, симметричное расположение частот, но разные степени рассеивания Пример: ряды распределения с разной 0 = степень рассеивания -3 -3 -1 0 0 1 3 3 =0 -9 -8 -6 0 1 1 2 2 3 14 Dr. Igor Arzhenovskiy

Статистика Показатели вариации Размах вариации: Интерквартильный размах: Среднее линейное отклонение: Дисперсия: Среднее квадратическое (стандартное) отклонение: Коэффициент вариации: Соотношение σ и l : Dr. Igor Arzhenovskiy

Статистика Пример расчета показателей вариации Дан ряд: 1; 2; 3; 4; 5. Тогда: Dr. Igor Arzhenovskiy

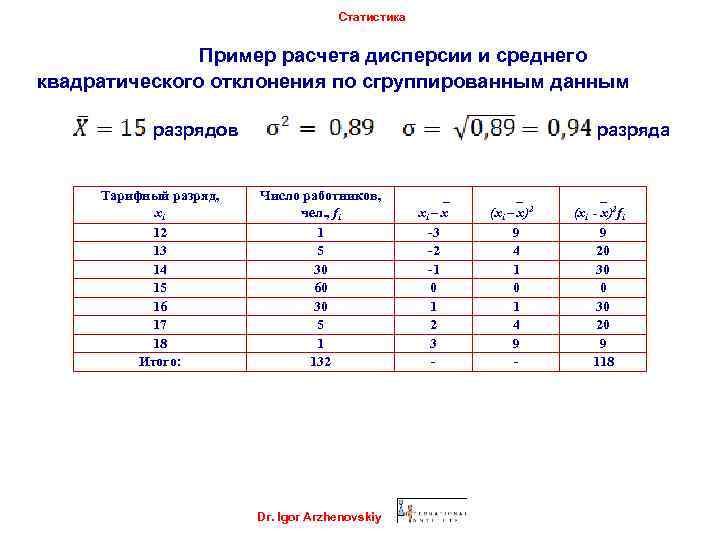Статистика Пример расчета дисперсии и среднего квадратического отклонения по сгруппированным данным разрядов Тарифный разряд, xi 12 13 14 15 16 17 18 Итого: разряда Число работников, чел. , fi 1 5 30 60 30 5 1 132 Dr. Igor Arzhenovskiy _ xi – x -3 -2 -1 0 1 2 3 - _ (xi – x)2 9 4 1 0 1 4 9 - _ (xi - x)2 fi 9 20 30 20 9 118

Статистика Свойства дисперсии σ2(const) = 0 σ2(X - А) = σ2 X σ2(X / K) = σ2 X : k 2 σ (X / K) = σX : k Dr. Igor Arzhenovskiy

Статистика Пример на правило сложения дисперсии Регион 1 2 3 Итого: общ. Средняя по региону (группе) Xi 3 4 5 - Вес, fi = (3∙ 1 + 4∙ 2 + 5∙ 3)/6 = 4, 3 α² = (1∙ 1 + 1∙ 2 + 3∙ 3)/6 = 2 σ2 общ. = δ 2 + α² = 0, 56 + 2 = 2, 56 Dr. Igor Arzhenovskiy 1 2 3 6 Дисперсия по региону (группе), σi 2 1 1 3

Статистика Расчет средней арифметической и показателей вариации для качественных (атрибутивных) признаков Значение переменной, Х 0 1 Итого: = = Частота f n–f n (1 – p) = q Пример. В результате контроля качества из 1000 готовых изделий 20 оказались бракованными. Нужно вычислить дисперсию и стандартное отклонение по данному номинально измеряемому признаку. Dr. Igor Arzhenovskiy

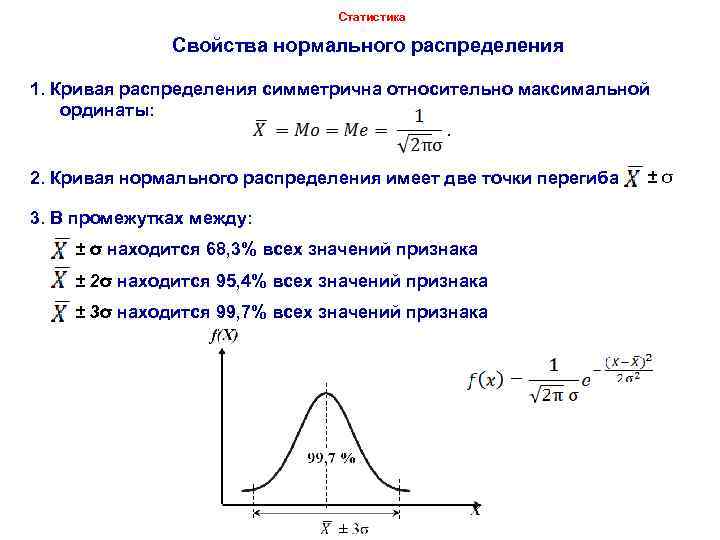Статистика Свойства нормального распределения 1. Кривая распределения симметрична относительно максимальной ординаты: 2. Кривая нормального распределения имеет две точки перегиба 3. В промежутках между: ± σ находится 68, 3% всех значений признака ± 2σ находится 95, 4% всех значений признака ± 3σ находится 99, 7% всех значений признака Dr. Igor Arzhenovskiy ±σ

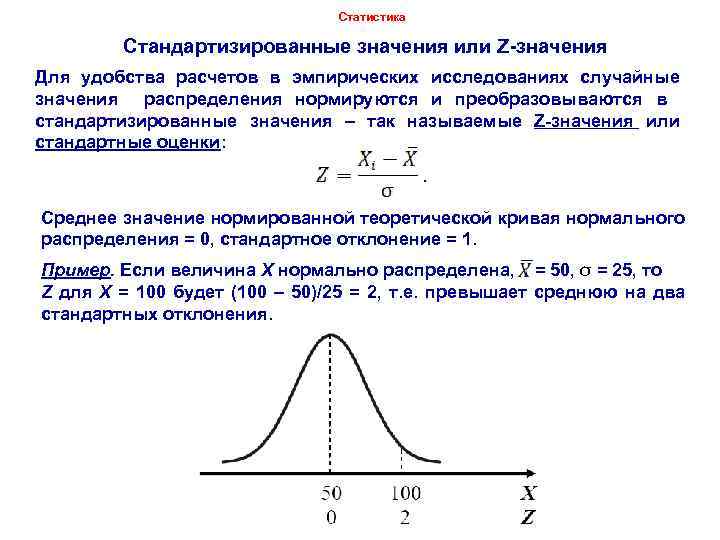Статистика Стандартизированные значения или Z-значения Для удобства расчетов в эмпирических исследованиях случайные значения распределения нормируются и преобразовываются в стандартизированные значения – так называемые Z-значения или стандартные оценки: Среднее значение нормированной теоретической кривая нормального распределения = 0, стандартное отклонение = 1. Пример. Если величина Х нормально распределена, = 50, σ = 25, то Z для X = 100 будет (100 – 50)/25 = 2, т. е. превышает среднюю на два стандартных отклонения. Dr. Igor Arzhenovskiy

Статистика Моменты – универсальные характеристики ряда распределения, средние арифметические тех или иных степеней отклонений значений признака от определенной исходной величины А: При А = 0 момент называется начальным, При А = момент называется центральным При А = условной величине момент называется условным Моменты распределения, порядка Начальные Первого Второго Третьего Четвертого Dr. Igor Arzhenovskiy Центральные Условные

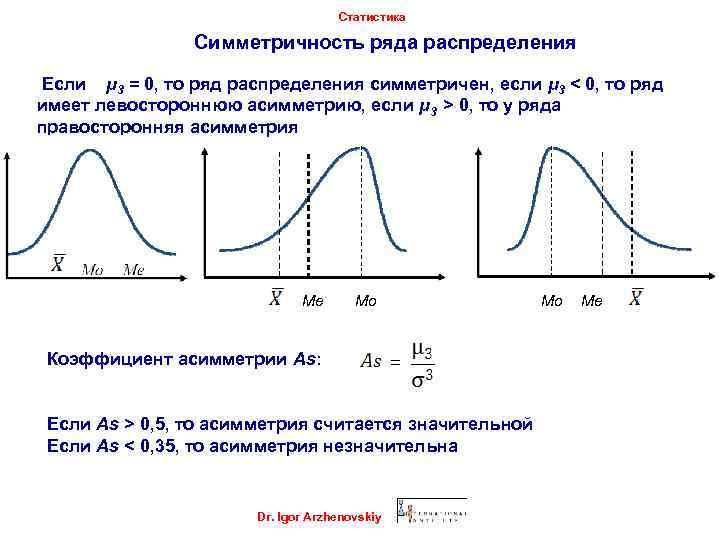Статистика Симметричность ряда распределения Если μ 3 = 0, то ряд распределения симметричен, если μ 3 < 0, то ряд имеет левостороннюю асимметрию, если μ 3 > 0, то у ряда правосторонняя асимметрия Ме Мо Коэффициент асимметрии Аs: Мо = Если As > 0, 5, то асимметрия считается значительной Если As < 0, 35, то асимметрия незначительна Dr. Igor Arzhenovskiy Ме

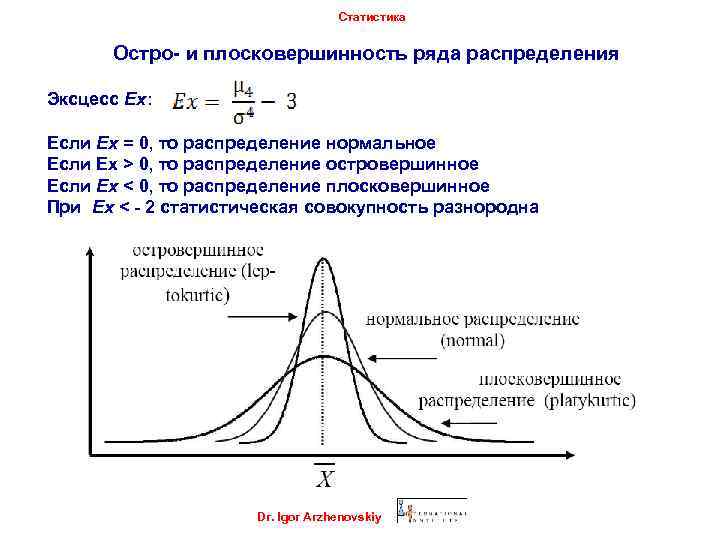Статистика Остро- и плосковершинность ряда распределения Эксцесс Ex: Если Ex = 0, то распределение нормальное Если Ex > 0, то распределение островершинное Если Ex < 0, то распределение плосковершинное При Ex < - 2 статистическая совокупность разнородна Dr. Igor Arzhenovskiy

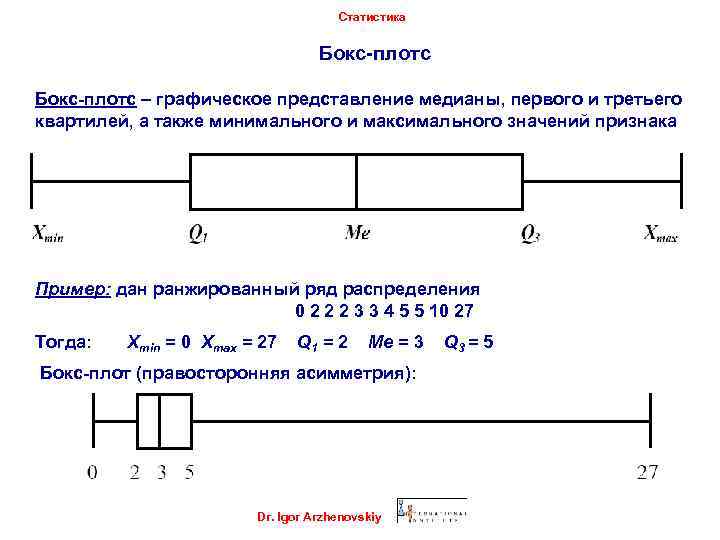Статистика Бокс-плотс – графическое представление медианы, первого и третьего квартилей, а также минимального и максимального значений признака Пример: дан ранжированный ряд распределения 0 2 2 2 3 3 4 5 5 10 27 Тогда: Хmin = 0 Xmax = 27 Q 1 = 2 Me = 3 Бокс-плот (правосторонняя асимметрия): Dr. Igor Arzhenovskiy Q 3 = 5

Статистика Тема 6. Индексы 1. Понятие об индексах 2. Индивидуальные индексы 3. Сводные индексы 4. Практика применения индексов в экономике Dr. Igor Arzhenovskiy

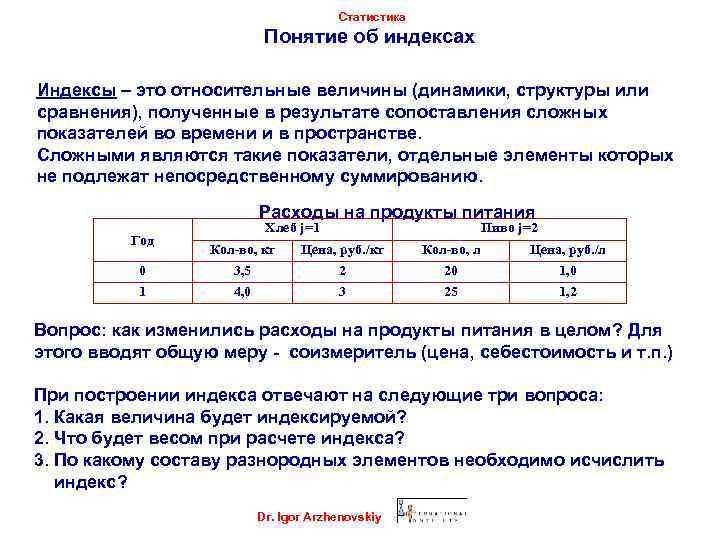Статистика Понятие об индексах Индексы – это относительные величины (динамики, структуры или сравнения), полученные в результате сопоставления сложных показателей во времени и в пространстве. Сложными являются такие показатели, отдельные элементы которых не подлежат непосредственному суммированию. Расходы на продукты питания Год Хлеб j=1 Пиво j=2 Кол-во, кг Цена, руб. /кг Кол-во, л Цена, руб. /л 0 3, 5 2 20 1, 0 1 4, 0 3 25 1, 2 Вопрос: как изменились расходы на продукты питания в целом? Для этого вводят общую меру - соизмеритель (цена, себестоимость и т. п. ) При построении индекса отвечают на следующие три вопроса: 1. Какая величина будет индексируемой? 2. Что будет весом при расчете индекса? 3. По какому составу разнородных элементов необходимо исчислить индекс? Dr. Igor Arzhenovskiy

Статистика Индивидуальные индексы отражают изменение только одного элемента сложного показателя. Пример: индивидуальный индекс цен Вывод: цена на хлеб возросла на 50 %, цена на пиво – на 20 % Dr. Igor Arzhenovskiy

Статистика Сводные индексы определяют изменение всех элементов сложного показателя Пример: индекс стоимости Вывод: расходы в целом возросли на 55, 6%. Dr. Igor Arzhenovskiy

Статистика Индексы цен и физического объема по Ласпейресу и Пааше Индекс цен по Ласпейресу: Индекс физического объема по Ласпейресу Dr. Igor Arzhenovskiy

Статистика Индексы цен и физического объема по Ласпейресу и Пааше Индекс цен по Пааше: Индекс физического объема по Пааше Взаимосвязь между индексами цен, физического объема и стоимости: Dr. Igor Arzhenovskiy

Статистика Средний арифметический индекс В нашем примере: Dr. Igor Arzhenovskiy

Статистика Средний гармонический индекс В нашем примере: Dr. Igor Arzhenovskiy

Статистика Некоторые правила исчисления индексов 1. Произведение рядом стоящих цепных индексов дает базисный индекс: 2. Частное от деления двух рядом стоящих базисных индексов дает цепной индекс: Для сводных индексов эти правила верны только в случае постоянных весов! Dr. Igor Arzhenovskiy

Статистика Некоторые правила исчисления индексов 3. Индекс структурных сдвигов: где Ix – индекс переменного состава, рассчитываемый путём сопоставления средних величин Ix - индекс постоянного состава, рассчитываемый по постоянной структуре явления Dr. Igor Arzhenovskiy

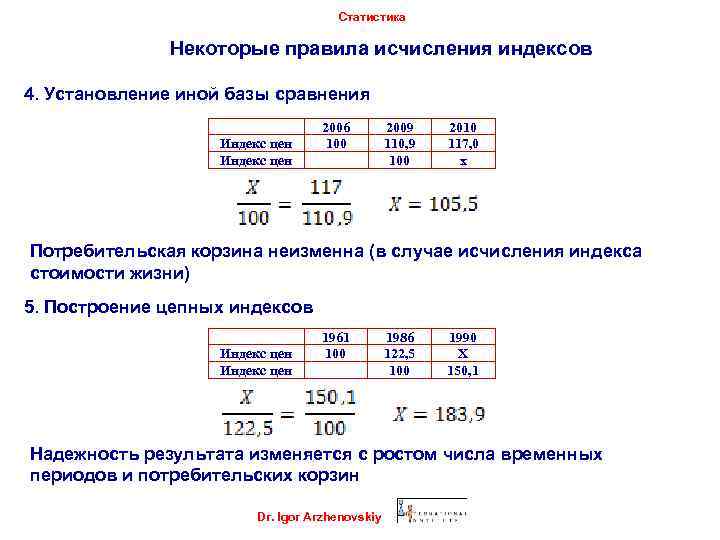Статистика Некоторые правила исчисления индексов 4. Установление иной базы сравнения Индекс цен 2006 100 2009 110, 9 100 2010 117, 0 x Потребительская корзина неизменна (в случае исчисления индексa стоимости жизни) 5. Построение цепных индексов Индекс цен 1961 100 1986 122, 5 100 1990 X 150, 1 Надежность результата изменяется с ростом числа временных периодов и потребительских корзин Dr. Igor Arzhenovskiy

Статистика Пример применение индексов в экономике Расчет паритета покупательной способности ППС показывает, сколько иностранной валюты должно быть израсходовано для покупки потребительской корзины, которую внутри страны приобретают на отечественную валюту (в расчете на единицу) Страна 1 Страна 2 Потребление товаров в кг А В С 10 7 14 5 11 13 Цены за кг (в соотв. валюте) А В С 5 3 4 2 2, 5 2 С точки зрения страны 2: Вывод: потребительская корзина по стране 2 стоит в стране 1 на 73% больше, чем в стране 2 Dr. Igor Arzhenovskiy

Статистика Тема 7. Измерение уровня концентрации 1. Постановка проблемы 2. Показатели концентрации 3. Применение методов измерения уровня концентрации в экономике Dr. Igor Arzhenovskiy

Статистика Постановка проблемы Измерение уровня концентрации заключается: - в определении степени концентрации изучаемого признака по единицам совокупности (абсолютная концентрация) - в оценке равномерности распределения признака по единицам совокупности (относительная концентрация) Пример 1, абсолютная концентрация: на рынке определённого товара 3 наиболее крупных предприятия имеют совокупную долю 90% Пример 2, относительная концентрация: 1, 7 % населения обладают более, чем 70 % всего имущества Dr. Igor Arzhenovskiy

Статистика Показатели концентрации Для измерения относительной концентрации применяются: - кривая Лоренца - коэффициент Джини Для измерения абсолютной концентрации применяются: - коэффициент концентрации - индекс Герфиндаля - индекс Розенблюта - индекс Линда Dr. Igor Arzhenovskiy

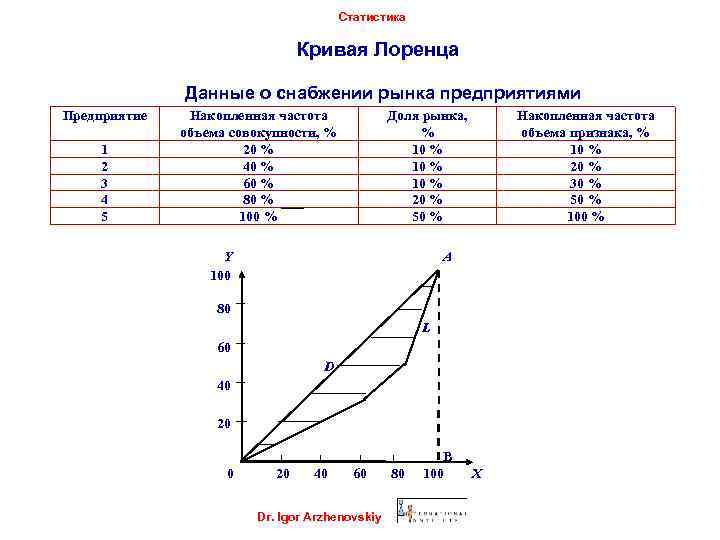Статистика Кривая Лоренца Данные о снабжении рынка предприятиями Предприятие 1 2 3 4 5 Накопленная частота объема совокупности, % 20 % 40 % 60 % 80 % 100 % Доля рынка, % 10 % 20 % 50 % Y 100 Накопленная частота объема признака, % 10 % 20 % 30 % 50 % 100 % A 80 L 60 D 40 20 40 60 Dr. Igor Arzhenovskiy 80 B 100 X

Статистика Коэффициент Джини Пример по немецкому варианту формулы: = 0, 36 Dr. Igor Arzhenovskiy

Статистика Коэффициент концентрации Пример: Индекс Герфиндаля Пример: Индекс Розенблюта Пример: Dr. Igor Arzhenovskiy

Статистика Экспоненциальный индекс Пример: Индекс Линда Пример: i=1 i=2 i=3 i=4 i=5 i= 6 i=7 i=8 pi 0, 4 0, 2 0, 15 0, 1 0, 08 0, 04 0, 02 0, 01 Ai 0, 4 0, 6 0, 75 0, 85 0. 93 0, 97 0, 99 1, 00 k=2 k=3 k=4 k=5 k=6 k=7 k=8 L 2 = 1 L 3 = 0, 71 L 4 = 0, 65 L 5 = 0, 56 L 6 = 0, 61 L 7 = 0, 74 L 8 = 0, 95 Dr. Igor Arzhenovskiy

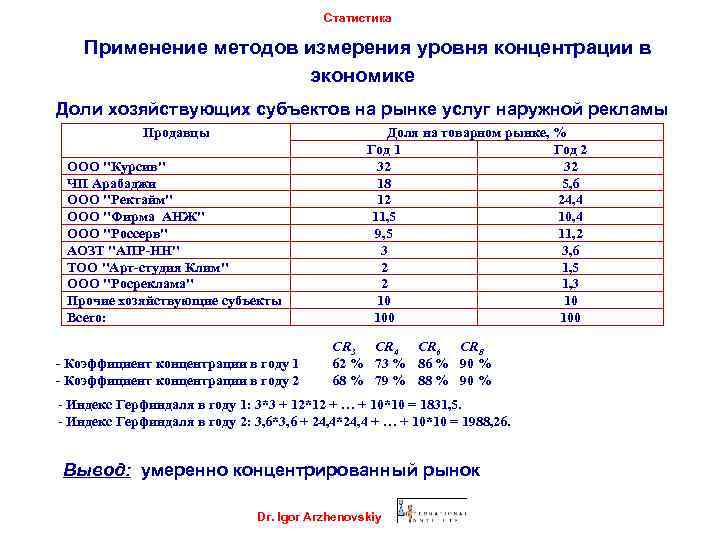Статистика Применение методов измерения уровня концентрации в экономике Доли хозяйствующих субъектов на рынке услуг наружной рекламы Продавцы ООО "Курсив" ЧП Арабаджи ООО "Ректайм" ООО "Фирма АНЖ" ООО "Россерв" АОЗТ "АПР-НН" ТОО "Арт-студия Клим" ООО "Росреклама" Прочие хозяйствующие субъекты Всего: - Коэффициент концентрации в году 1 - Коэффициент концентрации в году 2 Доля на товарном рынке, % Год 1 Год 2 32 32 18 5, 6 12 24, 4 11, 5 10, 4 9, 5 11, 2 3 3, 6 2 1, 5 2 1, 3 10 10 100 CR 3 CR 4 CR 6 CR 8 62 % 73 % 86 % 90 % 68 % 79 % 88 % 90 % - Индекс Герфиндаля в году 1: 3*3 + 12*12 + … + 10*10 = 1831, 5. - Индекс Герфиндаля в году 2: 3, 6*3, 6 + 24, 4*24, 4 + … + 10*10 = 1988, 26. Вывод: умеренно концентрированный рынок Dr. Igor Arzhenovskiy

Статистика Тема 8. Корреляционный и регрессионный анализ 1. Понятие корреляции и регрессии 2. Показатели корреляции 3. Регрессия Dr. Igor Arzhenovskiy

Статистика Понятие корреляции и регрессии Корреляция – изучение взаимосвязи двух или более величин Регрессия – нахождение аналитического выражения взаимосвязи двух или более величин, определение тенденции развития явления При изучении взаимосвязей одни признаки (факторные, Х) обуславливают изменение других признаков (результативных, Y) Задачи корреляционно-регрессионного анализа: - предварительный анализ статистической совокупности - установление связи, её направления и формы - установление степени тесноты связи - построение регрессионной модели - интерпретация и практическое использование результатов Dr. Igor Arzhenovskiy

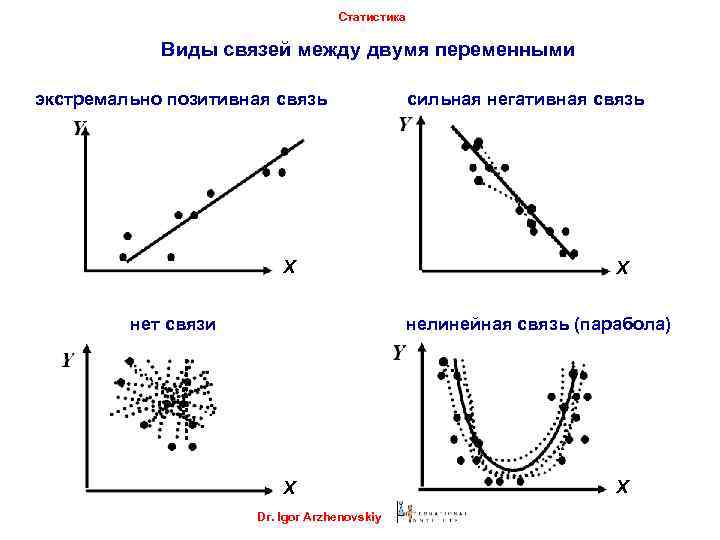Статистика Виды связей между двумя переменными экстремально позитивная связь Х нет связи сильная негативная связь Х нелинейная связь (парабола) Х Dr. Igor Arzhenovskiy Х

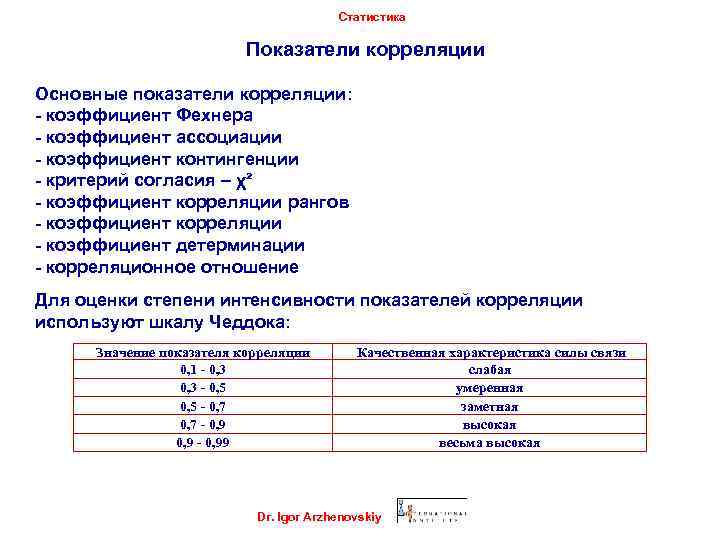Статистика Показатели корреляции Основные показатели корреляции: - коэффициент Фехнера - коэффициент ассоциации - коэффициент контингенции - критерий согласия – χ² - коэффициент корреляции рангов - коэффициент корреляции - коэффициент детерминации - корреляционное отношение Для оценки степени интенсивности показателей корреляции используют шкалу Чеддока: Значение показателя корреляции 0, 1 - 0, 3 - 0, 5 - 0, 7 - 0, 99 Качественная характеристика силы связи слабая умеренная заметная высокая весьма высокая Dr. Igor Arzhenovskiy

Статистика Коэффициент Фехнера где nс – число совпадений знаков отклонений индивидуальных величин от средне nн – число несовпадений знаков отклонений индивидуальных величин от средней Пример: Носитель признака 1 2 3 4 5 Факторный признак X 5 (+) 4 (-) 5 (+) Результативный признак Y 5 (+) 4 (-) 3 (-) Вывод: существует слабо выраженная негативная связь между X и Y Dr. Igor Arzhenovskiy

Статистика Коэффициенты ассоциации и контингенции По номинально измеряемым признакам можно рассчитать лишь коэффициент ассоциации или коэффициент контингенции Пример: Участники мероприятия Мужчины Женщины Спортсмены 20 (а) 15 (с) Не спортсмены 60 (в) 80 (d) Существует ли зависимость между двумя качественными признаками – Полом и отношением к спорту? Коэффициент ассоциации: Коэффициент контингенции: Вывод: существует слабо выраженная позитивная связь между полом и отношением к спорту Dr. Igor Arzhenovskiy

Статистика Критерий согласия χ² Пирсона где О – эмпирические (фактические) значения признаков Е – теоретические (выровненные) значения признаков Пример: зависит ли частота несчастных случаев от смены? Предварительная гипотеза: связь отсутствует Номер смены 1 2 3 Итого: Число несчастных случаев Фактическое Теоретически выровненное 1 5 7 5 15 15 Критериальное значение χ² с вероятностью 95% и числом степеней свободы n = 3 -1 = 2: χ² = 5, 99 > 4, 8 Вывод: различия между О и Е случайны, фактическое распределение не отличается существенно от теоретически выровненного. С 95 % вероятностью можно утверждать, что наша гипотеза верна Dr. Igor Arzhenovskiy

Статистика Коэффициент корреляции рангов по Спирмену где d – разность порядковых номеров (рангов) факторного и результативного признаков; n – число наблюдений Пример: стаж и производительность труда по 5 работникам № работника 1 2 3 4 5 Итого Стаж X 1 2 3 4 5 15 Ранг 1 2 3 4 5 Производительность Y Ранг 2 1 4 2 8 4 6 3 10 5 30 X*Y X² Y² d d² 2 8 24 24 50 108 1 4 9 16 25 55 4 16 64 36 100 220 0 0 -1 1 0 0 0 1 1 0 2 Вывод: существует сильная положительная зависимость между стажем и производительностью Dr. Igor Arzhenovskiy

Статистика Коэффициент корреляции по Бравис-Пирсону Пример: Вывод: существует сильная положительная зависимость между стажем и производительностью Dr. Igor Arzhenovskiy

Статистика Коэффициент детерминации Он показывает, какая часть колебаний результативного признака вызвана факторным признаком. В нашем примере 81% изменений в производительности труда вызван влиянием стажа работника. Корреляционное отношение где δ² – межгрупповая дисперсия; σобщ² – общая дисперсия совокупности Корреляционное отношение является универсальным показателем корреляции и применяется прямо- и –криволинейной зависимости. Коэффициент детерминации – η² Dr. Igor Arzhenovskiy

Статистика Ошибки показателей корреляции Для проверки значимости показателей корреляции рассчитывают их ошибки. Средние квадратические ошибки показателей корреляции имеют вид: Показатель корреляции должен в 2– 3 раза превосходить ошибку, чтобы с вероятностью 0, 95 (0, 997) говорить о связи между явлениями. При количестве наблюдений менее 30 (малая выборка) значимость показателей корреляции проверяют по t-критерию Стьюдента или z-преобразованию Фишера Dr. Igor Arzhenovskiy

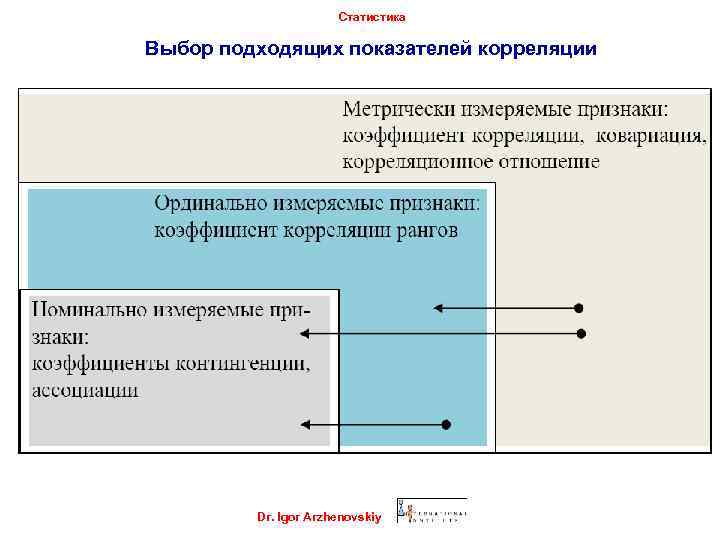Статистика Выбор подходящих показателей корреляции Dr. Igor Arzhenovskiy

Статистика Регрессия Этапы регрессионного анализа: 1. Определение функции (или типа кривой), которая наилучшим образом характеризует нашу зависимость. Такими функциями могут выступать: линейная гиперболическая параболическая степенная показательная логарифмическая y = ax +b y= a + b y = ax 2 + bx + c y = bxa y = bax y = loga х и другие Выбор кривой осуществляется либо визуально, либо с использованием метода последовательных разностей (для полиномов) Dr. Igor Arzhenovskiy

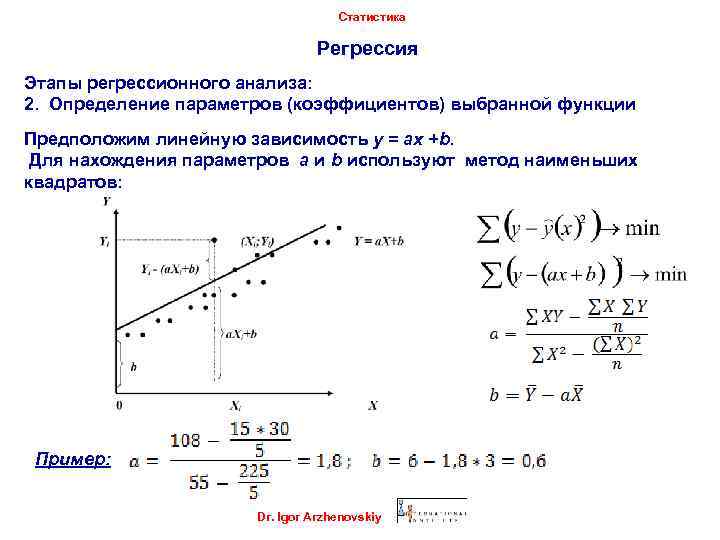Статистика Регрессия Этапы регрессионного анализа: 2. Определение параметров (коэффициентов) выбранной функции Предположим линейную зависимость y = ax +b. Для нахождения параметров a и b используют метод наименьших квадратов: Пример: Dr. Igor Arzhenovskiy

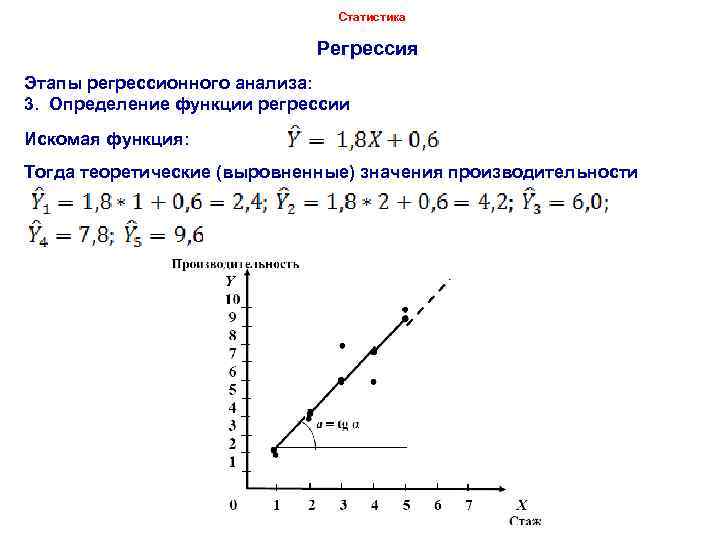Статистика Регрессия Этапы регрессионного анализа: 3. Определение функции регрессии Искомая функция: Тогда теоретические (выровненные) значения производительности Dr. Igor Arzhenovskiy

Статистика Регрессия Этапы регрессионного анализа: 4. Прогноз результативного признака При X = 5, 5 = 10, 5 при X = 6 = 11, 4 и т. д. Ограничения прогнозов: - стабильность неучтённых в модели факторов (внешней среды) - средняя квадратическая ошибка уравнения регрессии Dr. Igor Arzhenovskiy

Статистика Регрессия Этапы регрессионного анализа: 5. Проверка адекватности модели регрессии Значимость коэффициентов регрессии проводится с помощью t– критерия Стьюдента. Если tрасч > tтабл, то коэффициент статистически значим при уровне значимости α и числе степеней свободы v = n – k – 1, Для параметров а и b в случае простой парной регрессии имеем: Оценка надёжности модели регрессии проводится с помощью F–критерия Фишера – Снедекора. Для простой парной регрессии имеем: Если Fрасч > Fтабл при заданном уровне значимости α, то построенная модель признаётся надёжной и пригодной для аналитических и прогнозных расчётов Dr. Igor Arzhenovskiy

Статистика Регрессия Этапы регрессионного анализа: 5. Проверка адекватности модели регрессии Оценка средней ошибки аппроксимации Допустима ошибка 12 -15 % при заданном уровне значимости α Пример: в полученном уравнении прямой регрессии ta расч = 3, 6 > ta табл = 3, 18 при α = 0, 05, т. е. параметр а статистически значим tb расч = 0, 34 < tb табл = 3, 18 при α = 0, 05, т. е. параметр b статистически незначим Fрасч = 12, 79 > F табл = 10, 13 при α = 0, 05, т. е. уравнение в целом надёжно и пригодно для дальнейших прогнозов = 16, 8 %, т. е. качество модели недостаточно хорошее, что не позволяет надеяться на точный прогноз. Dr. Igor Arzhenovskiy