СТАТИСТИКА Семинар 9 Тема Показатели вариации продолжение

СТАТИСТИКА Семинар № 9 Тема: «Показатели вариации: продолжение»

РАЗМАХ ВАРИАЦИИ Размах вариации - это разность между наибольшим и наименьшим значениями вариант (признаков): Группы предприятий по объему Число товарооборота, млн. руб. предприятий 90 — 100 28 100 — 110 48 110 — 120 24 ИТОГО 100 Определяем показатель размаха вариации: R = 120 - 90 = 30 млн. руб.

СРЕДНЕЕ ЛИНЕЙНОЕ ОТКЛОНЕНИЕ. Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений: / Итого: 2 3 12 15 18 50 -8 -7 2 5 8 0 / 8 7 2 5 8 30

СРЕДНЕЕ ЛИНЕЙНОЕ ОТКЛОНЕНИЕ Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:

ДИСПЕРСИЯ Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается. В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной: — дисперсия невзвешенная (простая); — дисперсия взвешенная.

ДИСПЕРСИЯ Дисперсия может быть также рассчитана как разность между средним квадратом значений признака и квадратом их среднего:

: СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты признака от среднего значения. Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается — среднее квадратическое отклонение невзвешенное; — среднее квадратическое отклонение взвешенное.

СВОЙСТВО СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ В условиях нормального распределения существует следующая взаимосвязь между величиной σ и количеством наблюдений: В пределах располагается 0, 683 или 68, 3% количества всех наблюдений; В пределах располагается 0, 954 или 95, 4% количества всех наблюдений; В пределах располагается 0, 997 или 99, 7% количества всех наблюдений;

ПРИМЕР № 1 Произведено продукции 1 -им рабочим, шт. 8 9 10 11 12 ИТОГО Число рабочих, Рассчитать дисперсию с помощью формул: 1. 2. 7 10 15 12 6 50

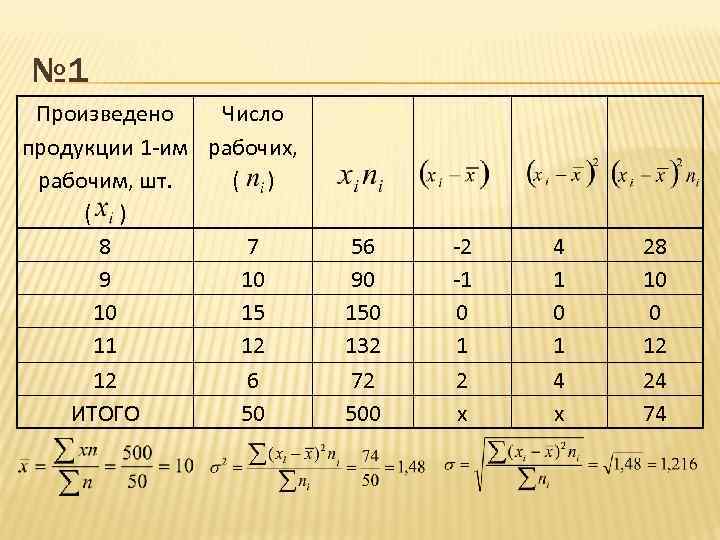№ 1 Произведено Число продукции 1 -им рабочих, рабочим, шт. ( ) 8 7 9 10 10 15 11 12 12 6 ИТОГО 50 56 90 150 132 72 500 -2 -1 0 1 2 x 4 1 0 1 4 x 28 10 0 12 24 74

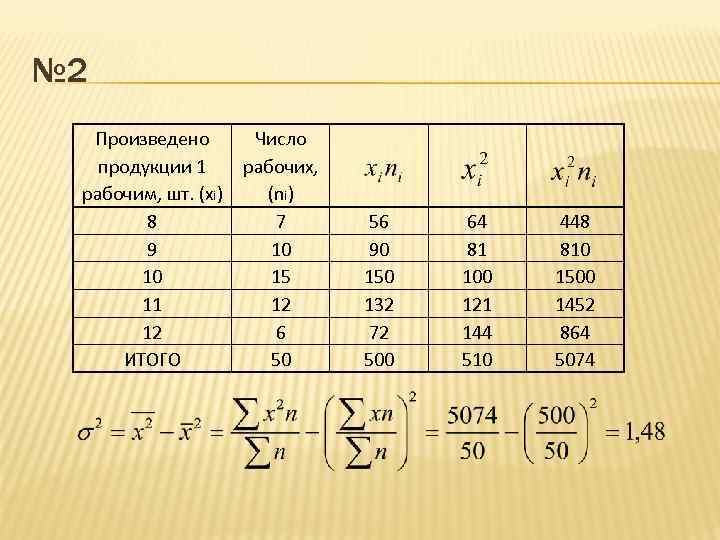№ 2 Произведено продукции 1 рабочим, шт. (хi) 8 9 10 11 12 ИТОГО Число рабочих, (ni) 7 10 15 12 6 50 56 90 150 132 72 500 64 81 100 121 144 510 448 810 1500 1452 864 5074

ПОКАЗАТЕЛИ ОТНОСИТЕЛЬНОГО РАССЕИВАНИЯ Показатели относительного рассеивания применяются для характеристики меры колеблемости изучаемого признака. Различают следующ ие относительные показатели вариации: Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней. Относительное линейное отклонение (линейный коэффициент вариации) - характеризует долю усредненного значения абсолютных отклонений от средней величины. Коэффициент вариации - показывает, какую долю среднего значения случайной величины составляет ее средний разброс.

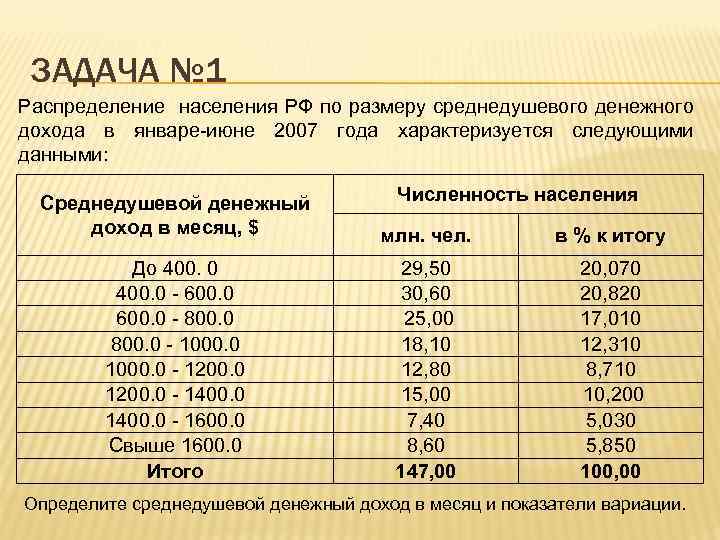ЗАДАЧА № 1 Распределение населения РФ по размеру среднедушевого денежного дохода в январе-июне 2007 года характеризуется следующими данными: Численность населения Среднедушевой денежный доход в месяц, $ млн. чел. в % к итогу До 400. 0 - 600. 0 - 800. 0 - 1000. 0 - 1200. 0 - 1400. 0 - 1600. 0 Свыше 1600. 0 Итого 29, 50 30, 60 25, 00 18, 10 12, 80 15, 00 7, 40 8, 60 147, 00 20, 070 20, 820 17, 010 12, 310 8, 710 10, 200 5, 030 5, 850 100, 00 Определите среднедушевой денежный доход в месяц и показатели вариации.

ДОМАШНЕЕ ЗАДАНИЕ Дорешать Решить недорешанные задачи. задачу № 1 (из ДЗ) Прочитать главу «Показатели вариации» (особое внимание разделу «Свойства дисперсии» )

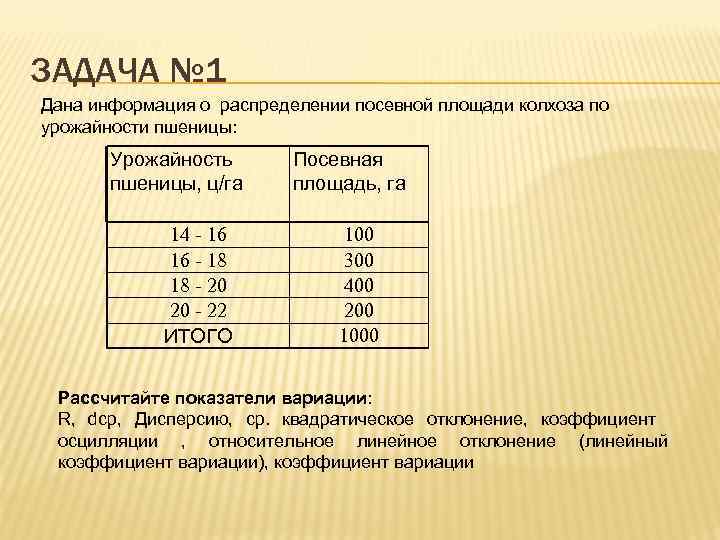ЗАДАЧА № 1 Дана информация о распределении посевной площади колхоза по урожайности пшеницы: Урожайность пшеницы, ц/га 14 - 16 16 - 18 18 - 20 20 - 22 ИТОГО Посевная площадь, га 100 300 400 200 1000 Рассчитайте показатели вариации: R, dcp, Дисперсию, ср. квадратическое отклонение, коэффициент осцилляции , относительное линейное отклонение (линейный коэффициент вариации), коэффициент вариации