Статистика_11сем_Выборочное наблюдение.ppt
- Количество слайдов: 20

СТАТИСТИКА Семинар № 11 Тема: «Выборочное наблюдение»

ОПРЕДЕЛЕНИЕ Выборочное наблюдение – это такое несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность.

ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА В выборочном наблюдении используются понятия: «генеральная совокупность» — изучаемая совокупность единиц, подлежащая изучению по интересующим исследователя признакам, «выборочная совокупность» — случайно выбранная из генеральной совокупности некоторая ее часть.

СПОСОБЫ ОТБОРА В ВЫБОРОЧНУЮ СОВОКУПНОСТЬ Простая случайная выборка (собственно-случайная) - отбор единиц из ГС путем случайного отбора, но при условии вероятности выбора любой единицы из ГС (отбор методом жеребьевки или по таблице случайных чисел). Типическая (стратифицированная) выборка - разделение неоднородной ГС на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц. Для серийной (гнездовой) выборки характерно то, что ГС первоначально разбивается на определенные равновеликие или неравновеликие серии (единицы внутри серий связаны по определенному признаку), из которых путем случайного отбора отбираются серии и затем внутри отобранных серий проводится сплошное наблюдение. Механическая выборка - отбор единиц через равные промежутки (по алфавиту, через временные промежутки, по пространственному способу и т. д. ). При проведении механического отбора ГС разбивается на равные по численности группы, из которых затем отбирается по одной единице. Комбинированная выборка -сочетание нескольких способов выборки. Многоступенчатая выборка есть образование внутри ГС вначале крупных групп единиц, из которых образуются группы, меньшие по объему, и так до тех пор, пока не будут отобраны те группы или отдельные единицы, которые необходимо исследовать.

Выборочный отбор может быть повторным и бесповторным. При повторном отборе вероятность выбора любой единицы не ограничена. При бесповторном отборе выбранная единица в исходную совокупность не возвращается. Для отобранных единиц рассчитываются обобщенные показатели (средние или относительные) и в дальнейшем результаты выборочного исследования распространяются на всю генеральную совокупность. Основной задачей при выборочном исследовании является определение ошибок выборки. Принято различать среднюю и предельную ошибки выборки.

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРАЛЬНОЙ И ВЫБОРОЧНОЙ СОВОКУПНОСТЕЙ Характеристика Генеральная совокупность Выборочная совокупность Объем совокупности (численность единиц) N n Численность единиц, обладающих обследуемым признаком М m Доля единиц, обладающих обследуемым признаком р= M / N w=m/n Средний размер признака Дисперсия доли

ОШИБКИ ВЫБОРОЧНОГО НАБЛЮДЕНИЯ Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называется ошибкой статистического наблюдения.

ПРЕДЕЛЬНАЯ ОШИБКА ВЫБОРКИ При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки. Согласно теореме А. М. Ляпунова , вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной совокупности, подчиняется нормальному закону распределения и может быть найдена на основе интеграла Лапласа:
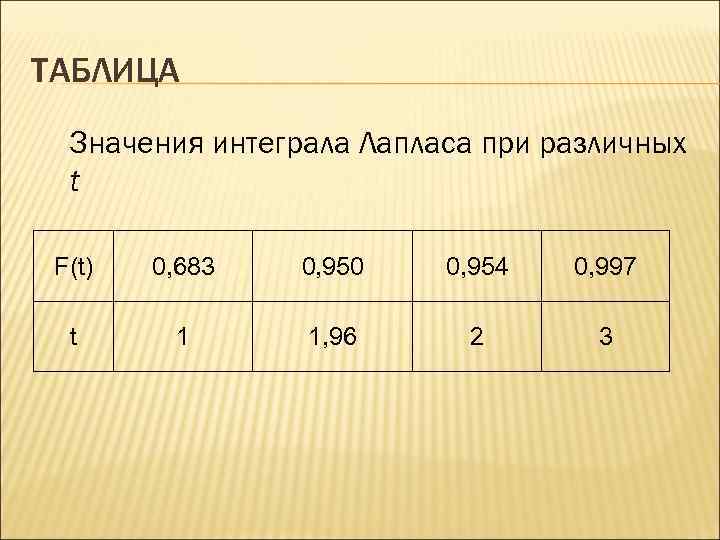
ТАБЛИЦА Значения интеграла Лапласа при различных t F(t) 0, 683 0, 950 0, 954 0, 997 t 1 1, 96 2 3

РАЗЛИЧАЮТ СРЕДНЮЮ (СТАНДАРТНУЮ) И ПРЕДЕЛЬНУЮ ОШИБКУ ВЫБОРКИ Под средней (стандартной) ошибкой выборки понимают такое расхождение между средней выборочной и генеральной совокупностью , которое не превышает ±Δ. С учетом выбранного уровня вероятности и соответствующего ему значения t предельная ошибка выборки равна:
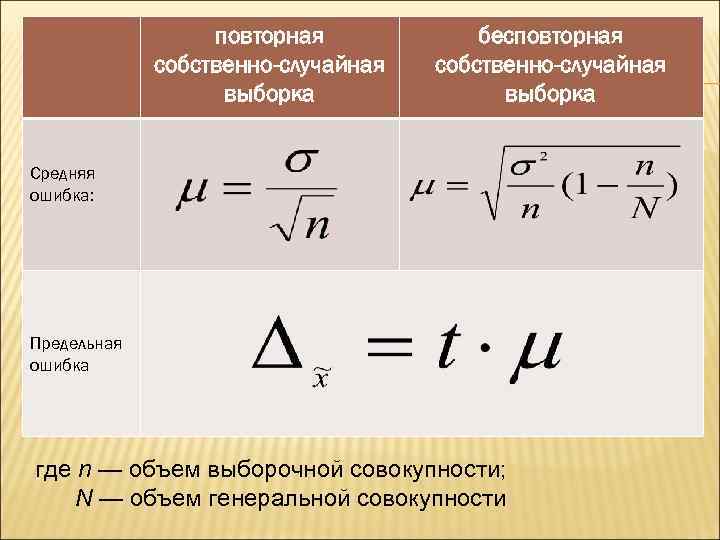
повторная собственно-случайная выборка бесповторная собственно-случайная выборка Средняя ошибка: Предельная ошибка определяется по формуле: Предельная ошибка где n — объем выборочной совокупности; N — объем генеральной совокупности

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ , Зная выборочную среднюю величину признака и предельную ошибку выборки , можно рассчитать границы (пределы), в которых заключена генеральная средняя:

ДИСПЕРСИЯ ДОЛИ Кроме определения ошибок выборки и пределов для генеральной средней эти же показатели могут быть рассчитаны для доли признака. В данном случае особенности расчета связаны с определением дисперсии доли, которая вычисляется по формуле: где w=m/n - доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки. Пределы доли признака в генеральной совокупности выглядят следующим образом:

ОПРЕДЕЛЕНИЕ НЕОБХОДИМОГО ОБЪЕМА ВЫБОРКИ Для определения необходимой численности выборки исследователь должен знать уровень точности выборочной совокупности с определенной вероятностью. В общем случае необходимая численность выборки прямо пропорциональна дисперсии признака и квадрату коэффициента доверия t 2

НЕОБХОДИМЫЙ ОБЪЕМ ВЫБОРКИ ДЛЯ НЕКОТОРЫХ СПОСОБОВ ФОРМИРОВАНИЯ ВЫБОРОЧНОЙ СОВОКУПНОСТИ Вид выборочного наблюдения Повторный отбор Собственно случайная выборка Бесповторный отбор а) при определении среднего размера признака б) при определении признака доли Механическая выборка То же Типичная выборка: То же а) при определении среднего размера признака б) при определении признака доли Серийная выборка: а) при определении среднего размера признака б) при определении признака доли
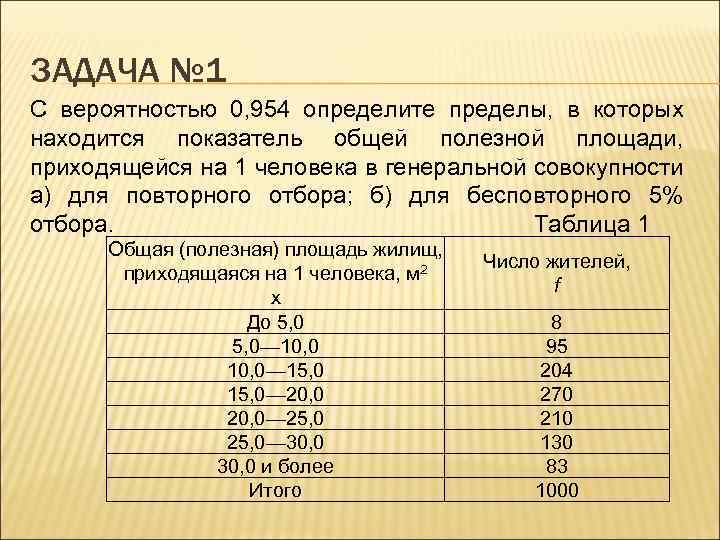
ЗАДАЧА № 1 С вероятностью 0, 954 определите пределы, в которых находится показатель общей полезной площади, приходящейся на 1 человека в генеральной совокупности a) для повторного отбора; б) для бесповторного 5% отбора. Таблица 1 Общая (полезная) площадь жилищ, приходящаяся на 1 человека, м 2 x До 5, 0— 10, 0— 15, 0— 20, 0— 25, 0— 30, 0 и более Итого Число жителей, f 8 95 204 270 210 130 83 1000

ЗАДАЧА № 2 По данным таблицы 1 определить границы доли лиц , обеспеченность жильем которых составляет менее 10 м 2.

ЗАДАЧА № 3 Какое количество деталей необходимо отобрать собственно-случайным повторным методом, чтобы ошибка выборки не превышала 3 мм с вероятностью 0, 997 при среднем квадратическом отклонении 6 мм? Рассчитать размер выборки для собственнослучайного бесповторного метода при размере генеральной совокупности 1000 шт.

ЗАДАЧА № 4 Из партии импортируемой продукции на посту таможни было взято в порядке случайной повторной выборки 20 проб продукта А. В результате проверки установлена средняя влажность продукта А в выборке, которая оказалась равной 6% при среднем квадратическом отклонении 1%. С вероятностью 0, 683 определите пределы средней влажности продукта во всей партии импортируемой продукции.

ДОМАШНЕЕ ЗАДАНИЕ № 11 1. Прочитать главу «Выборочное наблюдение» (учебник Шмойловой Р. А. ) 2. Дорешать недорешанные задачи
Статистика_11сем_Выборочное наблюдение.ppt