Statistics for Managers Using Microsoft Excel 5 th

Statistics for Managers Using Microsoft® Excel 5 th Edition Chapter 9 Fundamentals of Hypothesis Testing: One Sample Tests Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. Chap 9 -1

Learning Objectives In this chapter, you will learn: § The basic principles of hypothesis testing § How to use hypothesis testing to test a mean or proportion § The assumptions of each hypothesis-testing procedure, how to evaluate them, and the consequences if they are seriously violated § How to avoid the pitfalls involved in hypothesis testing § Ethical issues involved in hypothesis testing Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 2

The Hypothesis § A hypothesis is a claim (assumption) about a population parameter: § population mean Example: The mean monthly cell phone bill of this city is μ = $52 § population proportion Example: The proportion of adults in this city with cell phones is π =. 68 Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 3

The Null Hypothesis, H 0 § States the assumption (numerical) to be tested § Always contains “=” , “≤” or “ ” sign Example: The mean number of TV sets in U. S. Homes is equal to three. § Is always about a population parameter, not about a sample statistic. § May or may not be rejected Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 4

The Alternative Hypothesis, H 1 § Is the opposite of the null hypothesis § e. g. , The mean number of TV sets in U. S. homes is not equal to 3 ( H 1: μ ≠ 3 ) § Challenges the status quo § Never contains the “=” , “≤” or “ ” sign § May or may not be proven § For one tail tests is generally the hypothesis that the researcher is trying to prove Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 5

Hypothesis Testing § We assume the null hypothesis is true § If the null hypothesis is rejected we have proven the alternate hypothesis § If the null hypothesis is not rejected we have proven nothing as the sample size may have been to small Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 6

The Hypothesis Testing Process § Claim: The population mean age is 50. § H 0: μ = 50, H 1: μ ≠ 50 § Sample the population and find sample mean. Population Sample Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 7

The Hypothesis Testing Process § Suppose the sample mean age was X = 20. § This is significantly lower than the claimed mean population age of 50. § If the null hypothesis were true, the probability of getting such a different sample mean would be very small, so you reject the null hypothesis. § In other words, getting a sample mean of 20 is so unlikely if the population mean was 50, you conclude that the population mean must not be 50. Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 8

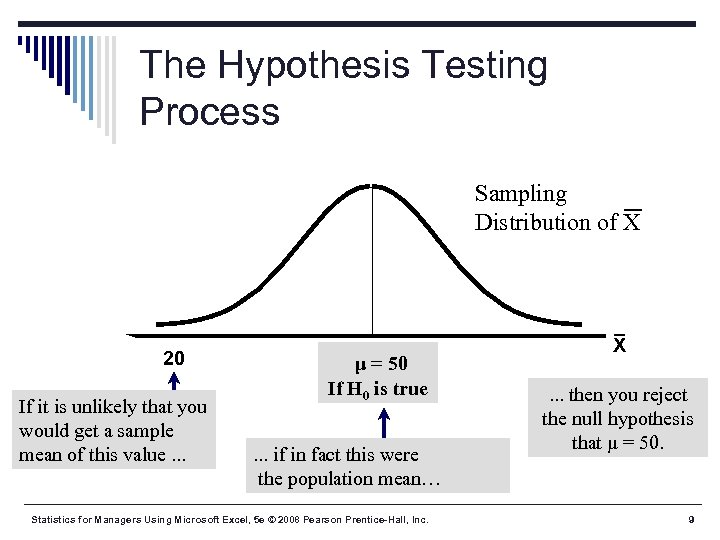The Hypothesis Testing Process Sampling Distribution of X 20 If it is unlikely that you would get a sample mean of this value. . . μ = 50 If H 0 is true. . . if in fact this were the population mean… Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. X. . . then you reject the null hypothesis that μ = 50. 9

The Test Statistic and Critical Values § If the sample mean is close to the assumed population mean, the null hypothesis is not rejected. § If the sample mean is far from the assumed population mean, the null hypothesis is rejected. § How far is “far enough” to reject H 0? § The level of significance of the test statistic ( ) creates a “line in the sand” for decision making. Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 10

Level of Significance, § Defines the unlikely values of the sample statistic if the null hypothesis is true § Defines rejection region of the sampling distribution § Is designated by , (level of significance) § Typical values are. 01, . 05, or. 10 § Is the compliment of the confidence coefficient § Is selected by the researcher before sampling § Provides the critical value of the test Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 11

The Test Statistic and Critical Values Distribution of the test statistic Region of Rejection Critical Values Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 12

Errors in Decision Making § Type I Error § Reject a true null hypothesis § Considered a serious type of error § The probability of a Type I Error is § Called level of significance of the test § Set by researcher in advance § Type II Error § Failure to reject false null hypothesis § The probability of a Type II Error is β Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 13

Errors in Decision Making Possible Jury Trial Outcomes The Truth The Verdict Innocent Guilty Innocent No Error Type II Error Guilty Type I Error No Error Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 14

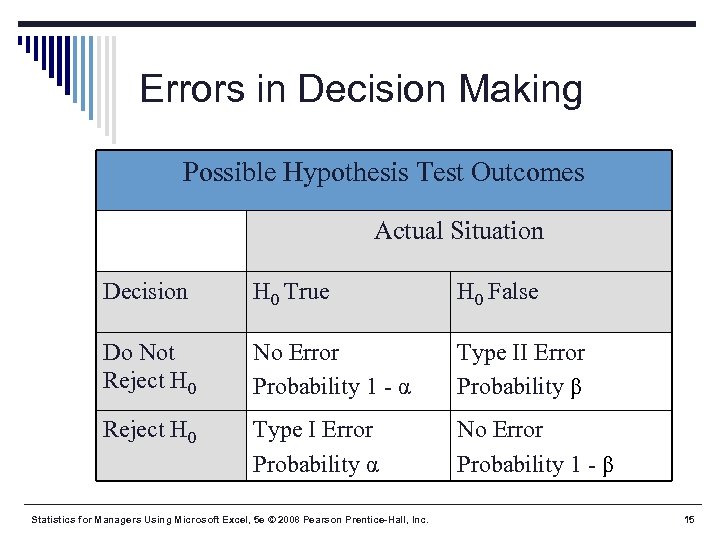Errors in Decision Making Possible Hypothesis Test Outcomes Actual Situation Decision H 0 True H 0 False Do Not Reject H 0 No Error Probability 1 - α Type II Error Probability β Reject H 0 Type I Error Probability α No Error Probability 1 - β Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 15

Type I & II Error Relationship § Type I and Type II errors can not happen at the same time § Type I error can only occur if H 0 is true § Type II error can only occur if H 0 is false If Type I error probability ( ) , then Type II error probability ( β ) Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 16

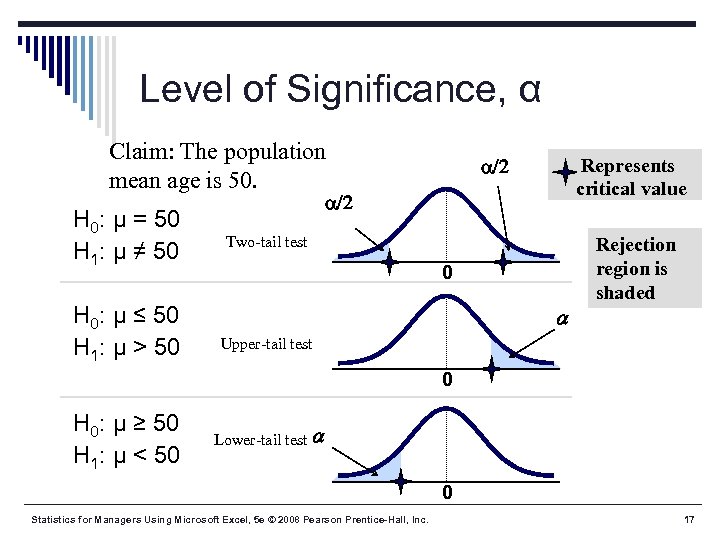Level of Significance, α Claim: The population mean age is 50. H 0: μ = 50 H 1: μ ≠ 50 H 0: μ ≤ 50 H 1: μ > 50 /2 Represents critical value /2 Two-tail test 0 a Rejection region is shaded Upper-tail test 0 H 0: μ ≥ 50 H 1: μ < 50 Lower-tail test a 0 Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 17

8 Steps in Hypothesis Testing 1. State the null hypothesis, H 0 State the alternative hypotheses, H 1 2. Choose the level of significance, α 3. Choose the sample size, n 4. Determine the appropriate test statistic to use 5. Collect the data 6. Compute the p-value for the test statistic from the sample result 7. Make the statistical decision: Reject H 0 if the p-value is less than alpha 8. Express the conclusion in the context of the problem Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 18

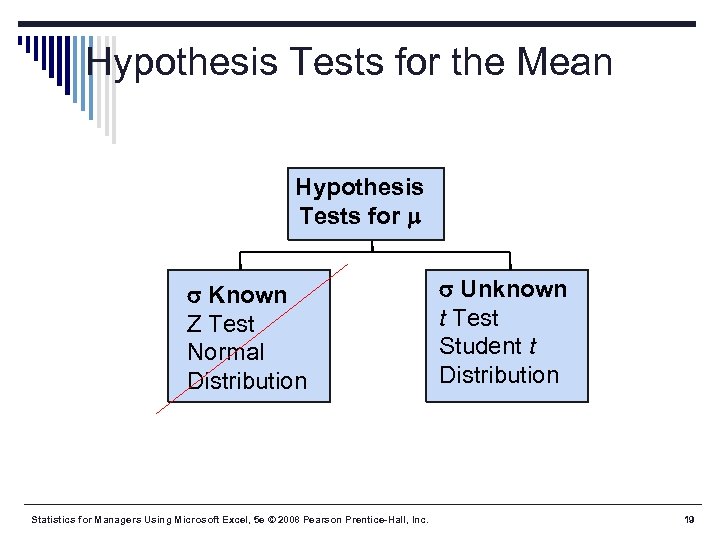Hypothesis Tests for the Mean Hypothesis Tests for Known Z Test Normal Distribution Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. Unknown t Test Student t Distribution 19

Hypothesis Testing: σ Unknown § If the population standard deviation is unknown, you use the sample standard deviation S instead of . § Because of this change, you also use the t distribution instead of the Z distribution to test the null hypothesis about the mean. § All other steps, concepts, and conclusions are the same as the known test. Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 20

Hypothesis Testing: σ Unknown § The t test statistic with n-1 degrees of freedom is: Hypothesized Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 21

Hypothesis Testing: σ Unknown Problem The mean cost of a hotel room in New York is said to be $168 per night. A random sample of 25 hotels resulted in X = $172. 50 and S = 15. 40. Test at the = 0. 05 level. Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 22

Hypothesis Testing Problem 8 steps § 1. State the appropriate null and alternative hypotheses H 0: μ = 168 H 1: μ ≠ 168 (This is a two tailed test) § 2. Specify the desired level of significance =. 05 is chosen for this test Choose a sample size sample of size n = 25 was selected Determine the appropriate Test σ is unknown so this is a t test § 3. § 4. Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 23

Hypothesis Testing Problem (continued) § 5. Collect the data The sample results are n = 25, § 6. X= $172. 50 S = $15. 40 So the test statistic is: The p value for n=25, =. 05, t=1. 4610 is. 1570 Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 24

Hypothesis Testing Problem (continued) § 7. Is the test statistic in the rejection region? Reject H 0 if p is < alpha; otherwise do not reject H 0 The p-value. 1570 is not < alpha. 05, we do not reject the null hypothesis Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 25

Hypothesis Testing Problem (continued) § 8. Express the conclusion in the context of the problem Since The p-value. 1570 is > alpha. 05, we have failed to reject the null hypothesis Thereby not proving the alternate hypothesis Conclusion: There is not sufficient evidence to reject the claim that the mean cost of a hotel room in NYC is $168 If we had rejected the null hypothesis the conclusion would have been: There is sufficient evidence to reject the claim that the mean cost of a hotel room in NYC is $168 Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 26

Hypothesis Testing: σ Unknown § Recall that you assume that the sample statistic comes from a random sample from a normal distribution. § If the sample size is small (< 30), you should use a box-and-whisker plot or a normal probability plot to assess whether the assumption of normality is valid. § If the sample size is large, the central limit theorem applies and the sampling distribution of the mean will be normal. Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 27

One Tail Tests § In many cases, the alternative hypothesis focuses on a particular direction H 0: μ ≥ 3 H 1: μ < 3 H 0: μ ≤ 3 H 1: μ > 3 This is a lower tail test since the alternative hypothesis is focused on the lower tail below the mean of 3 This is an upper tail test since the alternative hypothesis is focused on the upper tail above the mean of 3 Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 28

Hypothesis Testing: Connection to Confidence Intervals § For X = 172. 5, S = 15. 40 and n = 25, the 95% confidence interval is: 166. 14 ≤ μ ≤ 178. 86 § Since this interval contains the hypothesized mean (168), you do not reject the null hypothesis at =. 05 Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 29

Hypothesis Testing Proportions § Involves categorical variables § Two possible outcomes § “Success” (possesses a certain characteristic) § “Failure” (does not possesses that characteristic) § Fraction or proportion of the population in the “success” category is denoted by π Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 30

Hypothesis Testing Proportions § Sample proportion in the success category is denoted by p § When both nπ and n(1 -π) are at least 5, p can be approximated by a normal distribution with mean and standard deviation Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 31

Hypothesis Testing Proportions § The sampling distribution of p is approximately normal, so the test statistic is a Z value: Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 32

Hypothesis Testing Proportions Example A marketing company claims that it receives 8% responses from its mailing. To test this claim, a random sample of 500 were surveyed with 30 responses. Test at the =. 05 significance level. First, check: n π = (500)(. 08) = 40 n(1 -π) = (500)(. 92) = 460 Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 33

Hypothesis Testing Proportions Example H 0: π =. 08 H 1: π ≠. 08 α =. 05 n = 500, p = 30/500 =. 06 p-value for -1. 648 is. 0497 Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 34

Hypothesis Testing Proportions Example Test Statistic: p-value for -1. 648 is. 0497 Decision: Reject H 0 at =. 05 Conclusion: There is sufficient evidence to reject the company’s claim of 8% response rate. Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 35

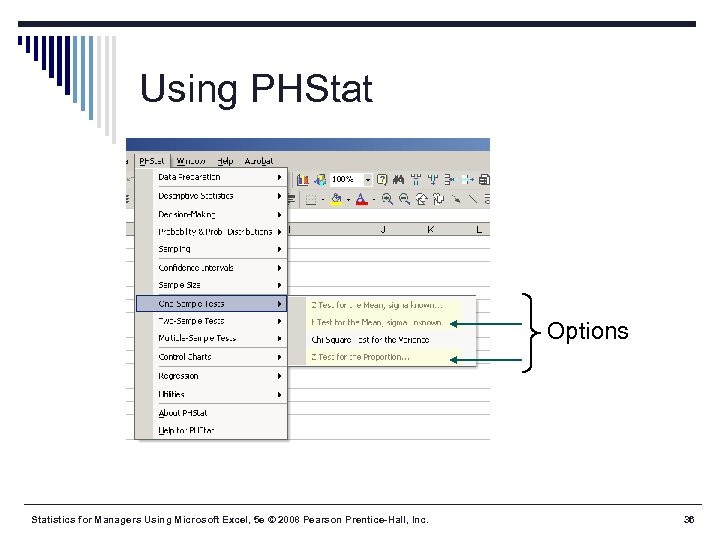Using PHStat Options Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 36

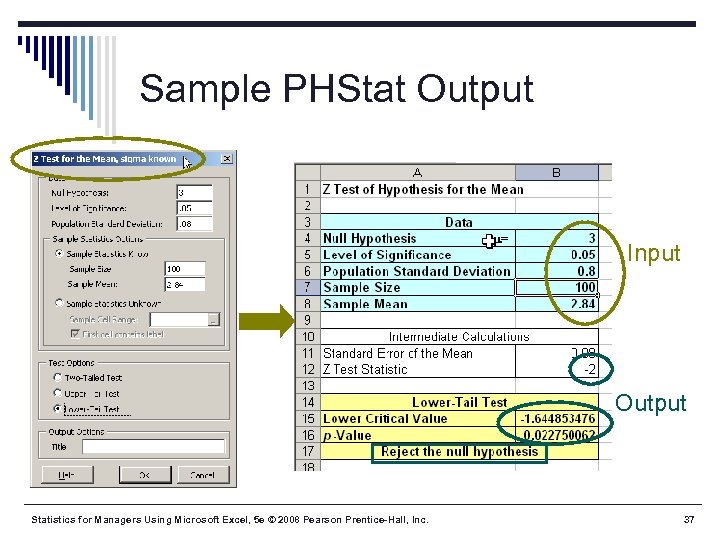Sample PHStat Output Input Output Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 37

Potential Pitfalls and Ethical Considerations § Use randomly collected data to reduce selection § § § biases Do not use human subjects without informed consent Choose the level of significance, α, before data collection Do not employ “data snooping” to choose between one-tail and two-tail test, or to determine the level of significance Do not practice “data cleansing” to hide observations that do not support a stated hypothesis Report all pertinent findings Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 38

Chapter Summary In this chapter, we have § Addressed hypothesis testing methodology § Mentioned Z Test for the mean (σ known) § Discussed the p–value approaches to hypothesis testing § Discussed one-tail and two-tail tests § Performed t test for the mean (σ unknown) § Performed Z test for the proportion § Discussed pitfalls and ethical issues Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 39

Answer Sheet for All Problems § ______ Null Hypothesis § ______ Alternate Hypothesis § ______ Alpha § ______ p-value § ______ Decision (reject or do not reject) § Conclusion: Statistics for Managers Using Microsoft Excel, 5 e © 2008 Pearson Prentice-Hall, Inc. 40