STATISTICS FOR MANAGERS LECTURE 3 LOOKING AT DATA

STATISTICS FOR MANAGERS LECTURE 3: LOOKING AT DATA AND MAKING INFERENCES

1. LOOKING AT DATA Central part of statistics: describing/ summarizing data n Take into account that data come in different types n Sales n Security rating n Sector n

1. 1 TYPES OF DATA n Qualitative/categorical n n n Attribute (nominal) data Ranked (ordinal) data Quantitative/numerical Different types of data require different treatment One can use: n n Graphical summaries Numerical summaries

1. 2 QUALITATIVE DATA n Graphical summaries Pie chart n Bar chart n Ordered bar chart n n Numerical summaries Frequency tables n Percentage tables n

1. 3 QUANTITATIVE DATA n Graphical summaries n n Run chart: Example: stock prices Histogram. Example: tick data Box plot Numerical summaries n n Arithmetic mean Median Standard deviation Quartiles

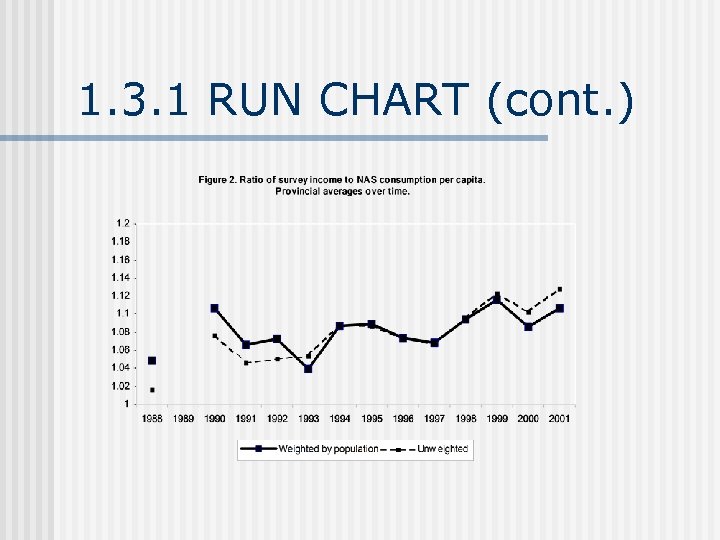
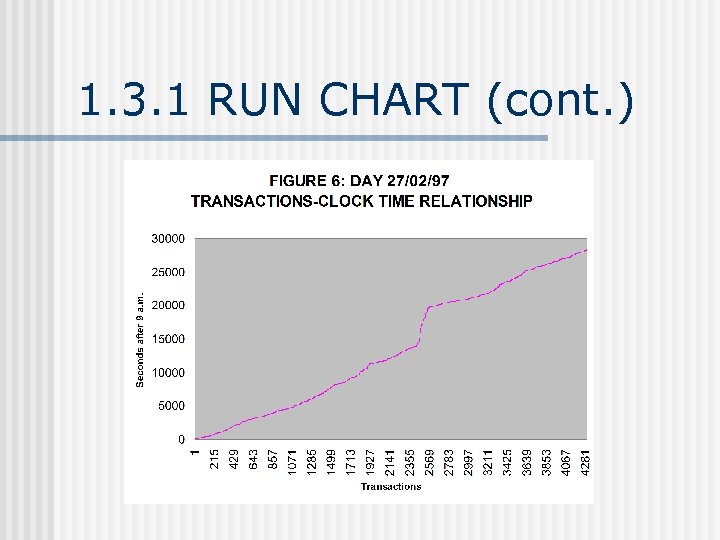
1. 3. 1 RUN CHART n n For data collected over time (time series) X-axis: date or number of data point Y-axis: numerical value of data point Things to look for n n Trends Seasonality Cycles Outliers

1. 3. 1 RUN CHART (cont. )

1. 3. 1 RUN CHART (cont. )

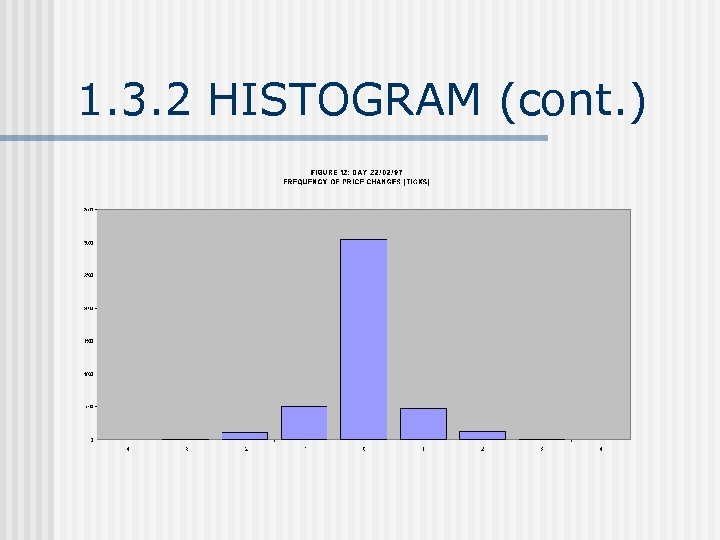
1. 3. 2 HISTOGRAM n n n Determine the range of data Decompose into bins of equal width Count how many data points fall within each bin Construct a bar chart based on these counts Only problem: have to choose the width of the bin Allows to judge n n Center/location Spread/variation Symmetry Outliers

1. 3. 2 HISTOGRAM (cont. )

1. 3. 3 BOX PLOT n Pack a lot of information in a single plot n n n Box that extend from Q 1 to Q 3 A line inside the box indicates the median Whiskers extend to bottom and top Outliers are denoted by asterisks Can compare data sets by lining up their box plots.

1. 3. 3 BOX PLOT (cont. )

1. 3. 4 LOCATION n n Mean: sum up all the data and divide by the number of points Median n Sort all the data from smallest to largest Take the middle one (for odd number of data) Take the average of the middle two (for even number of data)

1. 3. 4 LOCATION (cont. ) n Mean versus median n n The median is more robust than the mean. This means that it is less affected by extreme observations As a function of symmetry of the data • Skewed to the left: meanmedian n For skewed data the median is a more typical observation

1. 3. 5 SPREAD n Standard deviation n Measures a typical deviation from the mean Do not bother to do it yourself. Let EXCEL or any other program do it for you. Inter-quartile range n n n Q 1 is median of the bottom half of data Q 3 is median of the top half of data IQR=Q 3 -Q 1

1. 3. 6 OUTLIER DETECTION n Graphically n n n Use histogram Look for points away from the rest Numerically n n Points more than 3 standard deviations away from the mean Points more than 1. 5*IQR away from Q 1 and Q 3.

2. SAMPLING All statistical information is based on data n The process of collecting data is called sampling n It is important to do it right n Not everybody seems to understand this importance n

2. GENERAL SITUATION n n We study a population Can be a population in the strict sense but it could also be an experiment We are interested in certain characteristics of the population (parameter) Want to learn as much as possible about the parameter

2. EXAMPLES n Population of Beijing What is the average income? n What percentage speak Cantonese? n What percentage has Internet? n What is the average price of the square meter? (300. 000 euros buy only 174 squares meters). n What is the percentage of people that have a DVD? n

2. BASIC PROBLEM n n n Most populations are very large, or even infinite Hence it is typically impossible to exactly determine a parameter (sometime unfeasible from a cost perspective) But it is possible to learn something about a parameter By collecting a sample from the population we can obtain information But the quality of information cna only be as good as the quality of the sample

2. GOOD SAMPLE, IS THIS HARD? n n n The sample has to be representative of the population In collecting data, we must not favor (or disfavor) any particular segment of the population If we do we get biased samples Biased samples yield biased estimates. Example of biased samples: Internet.

2. NO VOLUNTEERS PLEASE n n n A sample into which people have entered at their own choice is called voluntary response sample or self-selected. This typically happens when polls are posted on the internet, the TV, . . The scheme favors people with strong opinions. The resulting sample is rarely representative of the population As so often you get what you pay for! (although something they pay for!)

2. HOW TO DO IT RIGHT n Analogy Have one ball per member of the population n Put all the balls in a big urn n Mix well n Take out n balls n The result is called simple random sample n

2. DO IT RIGHT. . . n There are other ways to get representative samples: Stratified sampling n Systematic sampling n Cluster sampling (multistage) n

2. . BUT AN ESTIMATE IS JUST THAT n n n We can estimate a parameter from the sample (a mean or a proportion). . . but an estimate is not equal to the parameter!. . . Because a sample is not equal to a population We must be aware of sampling error Many people are not! They sell us estimates as if they were parameters. Shame on them. Will do it right.

3. BASIC ESTIMATION n General estimation n n We are interested in a population parameter We collect a random sample In a first step we estimate the parameter. This is usually straighforward. In a second step, we deal with the sampling error. This requires more work but it is worhwhile.

3. 1. ESTIMATING A PROPORTION n n n n We are interested in a population proportion p We collect a random sample size n We compute the sample proportion This is a natural estimator for p, But due to the sampling error is not equal to the true parameter p Goal: quantify the sample uncertainty contained in the estimator of p Intuition: the larger n the smaller the uncertainty.

3. 1. ESTIMATING A PROPORTION n From probability theory we know that the central limit theorem applies, under some assumptions n For n large, then with a probability 95% the population proportion p will be in between n For the interval to be trusted we require

3. 1. ESTIMATING A PROPORTION A confidence interval has the following general form CI=estimator ±constant x std error (SE) =estimator ± margin of error (ME) For a proportion SE= The SE does not depend on the confidence level but the ME does because of the constant, which is often abbreviated as z

3. 1. ESTIMATING A PROPORTION How is the ME affected by its various inputs? ME= 1. 2. 3. As the confidence level increases the ME goes up. As the estimator moves towards 0. 5 the ME goes up As n increases the ME goes down We control de confidence level and n, but not the estimator of p

3. 1. ESTIMATING A PROPORTION Want a CI with a specified level and a specif ME? How large a sample size n is needed? Use ME and solve for n ME= Solution: Catch 22: we have not collected the sample yet, and therefore the estimate for p is not available yet. Solutions: 1. Worst case scenario estimator=0. 5 2. Use a guess based on previous information

WHAT CONFIDENCE LEVEL? n n You may want a confidence level other than 95%. Most common: 90%, 95% and 99%. The formula for the CI is equal You only change the constant 1. 96 Conf. Level n Constant z 90% 95% 99% 1. 64 1. 96 2. 57 Higher confidence level give a wider interval

3. 2. ESTIMATING A MEAN We are interested in a population mean and use as estimator the sample mean. CI=estimator ±constant x std error (SE) =estimator ± margin of error (ME) For a mean SE= CI= Rule of thumb: need more than 50 obs. To trust this interval

3. 2. ESTIMATING A MEAN How is the margin of error (ME) affected by its various inputs? ME= As confidence level increases, ME goes up 2. As s increases the ME goes up 3. As n increases the ME goes down We control n and conf. level but not s. 1.

3. 2. ESTIMATING A MEAN Want a CI with a specified level and a specif ME? How large a sample size n is needed? Use ME and solve for n ME= Solution: Catch 22: we have not collected the sample yet, and therefore the estimate for p is not available yet. In this case there is not worst case scenario. Use a guess based on previous information

3. 3. HYPOTHESIS TESTING If you care about wether a parameter is equal to a certain prespecified value, there is an alternative to hypothesis testing n Just check whether the prespecified value is contained in the confidence interval n

3. 3. HYPOTHESIS TESTING n If the prespecified value is contained in the CI n n n It is one of the (many) plausible values So we can only make a weak positive statement If the prespecified values is not contained in the CI n n It is not one of the plausible values We can make a strong negative statement

3. 3. CI PERFECT SUBSTITUTE n n n We wonder if a parameter is equal to a prespecified value? The technique of hypothesis testing give a “yesor-no” answer (at a certain level of significance) We can get the same from the level of confidence. . . But in addition we get the range of all plausible values! This is valuable info. Moral: a confidence interval tends to be safer and more informative than hypothesis testing

3. 4. CAVEAT n n n Our confidence intervals are simple, yet powerful. But you can’t use them blindly! Two conditions to trust them n n n We need a large sample We need a random sample Data that is collected over time is usually NOT a random sample: the data point of today is usually related to the data point yesterday Stock returns are an exception to this rule. Small sample and time series are for the pros!

3. 5. WHAT ABOUT OTHER PARAMETERS n n n We have covered confidence intervals for n Population proportions n Population means Both are based on the CLT There are other interesting parameters n Population median n Population standard deviation n etc Unfortunately they cannot be handle by the CLT CI can be constructed but the corresponding techniques are more difficult.