836c44b96f094460ddc4b676775e626e.ppt
- Количество слайдов: 47

Statistics for Business and Economics 8 th Edition Chapter 9 Hypothesis Testing: Single Population Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -1

9. 1 n What is a Hypothesis? A hypothesis is a claim (assumption) about a population parameter: n population mean Example: The mean monthly cell phone bill of this city is μ = $42 n population proportion Example: The proportion of adults in this city with cell phones is p =. 68 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -2

The Null Hypothesis, H 0 n States the assumption (numerical) to be tested Example: The average number of TV sets in U. S. Homes is equal to three ( ) A hypothesis about a parameter that will be maintained unless there is strong evidence against the null hypothesis. n Is always about a population parameter, not about a sample statistic Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -3

The Null Hypothesis, H 0 (continued) n n Begin with the assumption that the null hypothesis is true n Similar to the notion of innocent until proven guilty Always contains “=” , “≤” or “ ” sign May or may not be rejected A null hypothesis is a claim (or statement) about a population parameter that is assumed to be true until it is declared false. Ch. 9 -4

The Alternative Hypothesis, H 1 n n n Is the opposite of the null hypothesis n e. g. , The average number of TV sets in U. S. homes is not equal to 3 ( H 1: μ ≠ 3 ) Never contains the “=” , “≤” or “ ” sign May or may not be supported If we reject the null hypothesis, then the second hypothesis, named the “alternative hypothesis” will be accepted. Is generally the hypothesis that the researcher is trying to support An alternative hypothesis is a claim about a population parameter that will be true if the null hypothesis is false. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -5
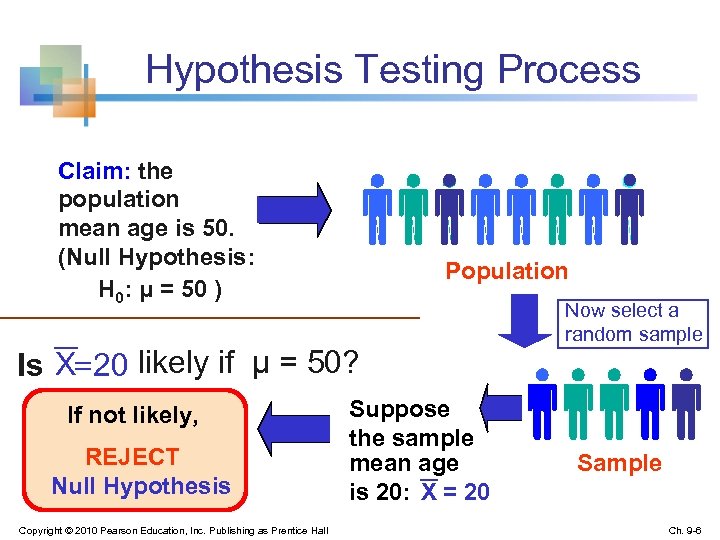
Hypothesis Testing Process Claim: the population mean age is 50. (Null Hypothesis: H 0: μ = 50 ) Population Is X= 20 likely if μ = 50? If not likely, REJECT Null Hypothesis Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Suppose the sample mean age is 20: X = 20 Now select a random sample Sample Ch. 9 -6
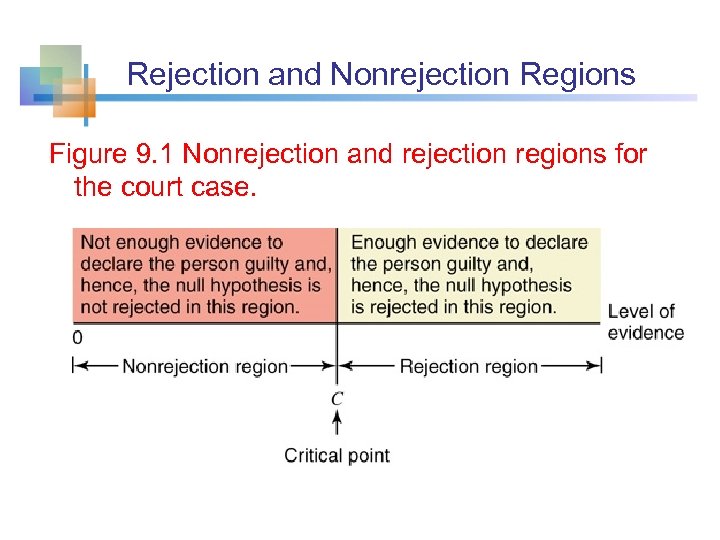
Rejection and Nonrejection Regions Figure 9. 1 Nonrejection and rejection regions for the court case.

Four Possible Outcomes for a Test of Hypothesis (Two Types of Errors) Actual Situation The person is not guilty Correct Decision Type 2 error The person is guilty Court's Decision The person is guilty Type 1 error Correct Decision Table: Four possible outcomes for a court case.

Two Types of Errors Definition A Type I error occurs when a true null hypothesis is rejected. The value of α represents the probability of committing this type of error; that is, α = P(H 0 is rejected | H 0 is true) The value of α represents the significance level of the test. A Type II error occurs when a false null hypotheses is not rejected. The value of β represents the probability of committing a Type II error; that is, β = P (H 0 is not rejected | H 0 is false) The value of 1 – β is called the power of the test. It represents the probability of not making a Type II error.

Level of Significance, n Defines the unlikely values of the sample statistic if the null hypothesis is true n n Defines rejection region of the sampling distribution Is designated by , (level of significance) n Typical values are. 01, . 05, or. 10 n Is selected by the researcher at the beginning n Provides the critical value(s) of the test Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -10
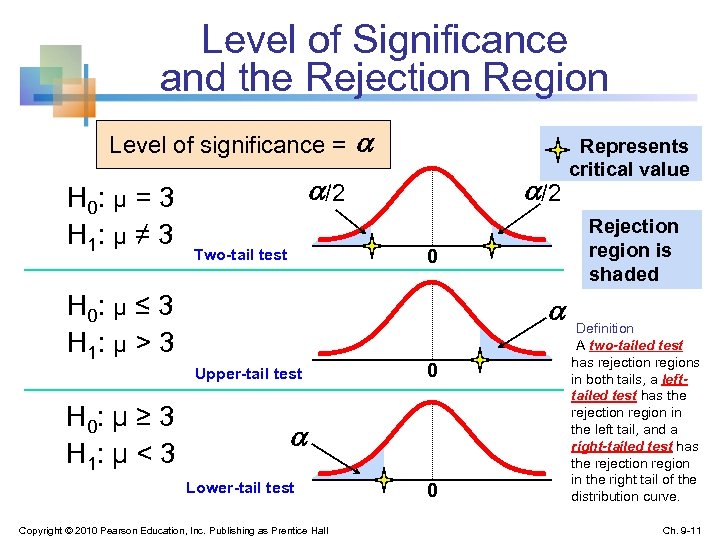
Level of Significance and the Rejection Region Level of significance = H 0: μ = 3 H 1: μ ≠ 3 /2 Upper-tail test 0 Lower-tail test Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 0 Represents critical value Rejection region is shaded 0 Two-tail test H 0: μ ≤ 3 H 1: μ > 3 H 0: μ ≥ 3 H 1: μ < 3 Definition A two-tailed test has rejection regions in both tails, a lefttailed test has the rejection region in the left tail, and a right-tailed test has the rejection region in the right tail of the distribution curve. Ch. 9 -11

Signs in H 0 and H 1 and Tails of a Test Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Hypothesis Tests for the Mean Hypothesis Tests for Known Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Unknown Ch. 9 -13

9. 2 n Test of Hypothesis for the Mean (σ Known) Convert sample result ( ) to a z value Hypothesis Tests for σ Known σ Unknown Consider the test The decision rule is: (Assume the population is normal) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -14
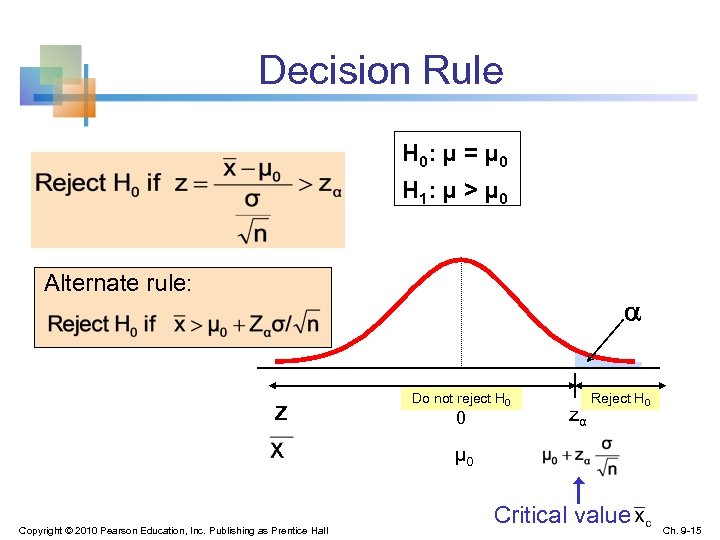
Decision Rule H 0: μ = μ 0 H 1: μ > μ 0 Alternate rule: Z Do not reject H 0 0 zα Reject H 0 μ 0 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Critical value Ch. 9 -15

Example 1: Upper-Tail Z Test for Mean ( Known) A phone industry manager thinks that customer monthly cell phone bill have increased, and now average over $52 per month. The company wishes to test this claim. (Assume = 10 is known) Form hypothesis test: H 0: μ ≤ 52 the average is not over $52 per month H 1: μ > 52 the average is greater than $52 per month (i. e. , sufficient evidence exists to support the manager’s claim) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -16
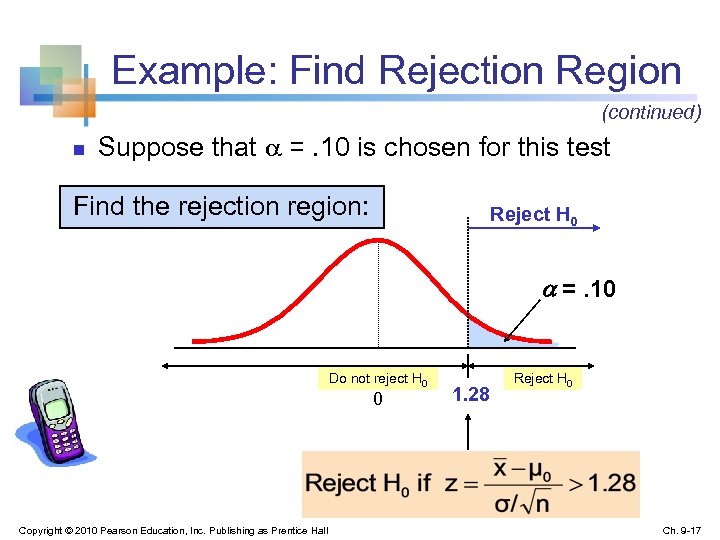
Example: Find Rejection Region (continued) n Suppose that =. 10 is chosen for this test Find the rejection region: Reject H 0 =. 10 Do not reject H 0 0 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 1. 28 Reject H 0 Ch. 9 -17

Example: Sample Results (continued) Obtain sample and compute the test statistic Suppose a sample is taken with the following results: n = 64, x = 53. 1 ( = 10 was assumed known) n Using the sample results, Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -18
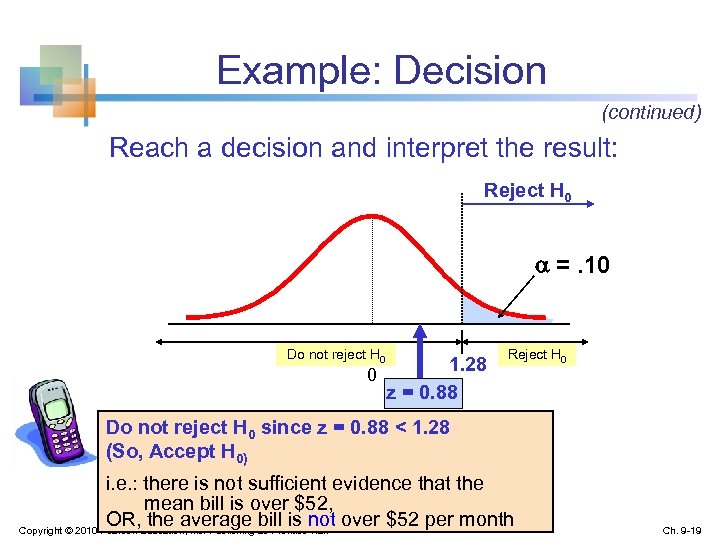
Example: Decision (continued) Reach a decision and interpret the result: Reject H 0 =. 10 Do not reject H 0 1. 28 0 z = 0. 88 Reject H 0 Do not reject H 0 since z = 0. 88 < 1. 28 (So, Accept H 0) i. e. : there is not sufficient evidence that the mean bill is over $52, OR, the average bill is not over $52 per month Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -19

One-Tail Tests n In many cases, the alternative hypothesis focuses on one particular direction H 0: μ ≤ 3 H 1: μ > 3 H 0: μ ≥ 3 H 1: μ < 3 This is an upper-tail test since the alternative hypothesis is focused on the upper tail above the mean of 3 This is a lower-tail test since the alternative hypothesis is focused on the lower tail below the mean of 3 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -20
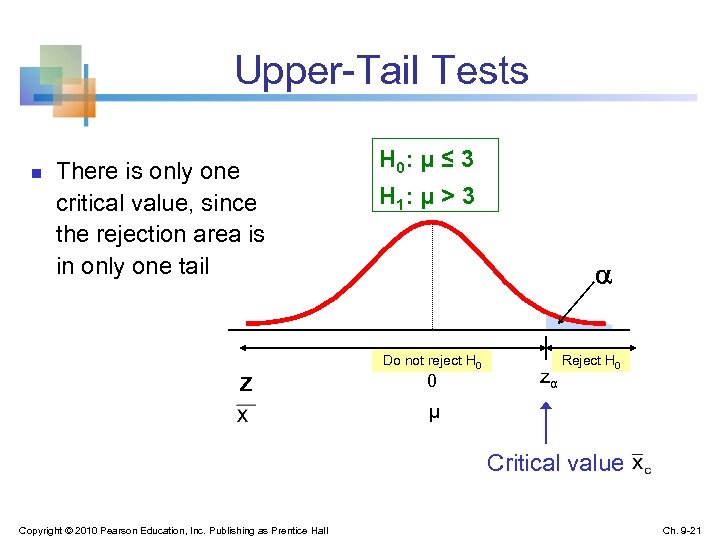
Upper-Tail Tests n There is only one critical value, since the rejection area is in only one tail H 0: μ ≤ 3 H 1: μ > 3 Do not reject H 0 Z 0 zα Reject H 0 μ Critical value Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -21
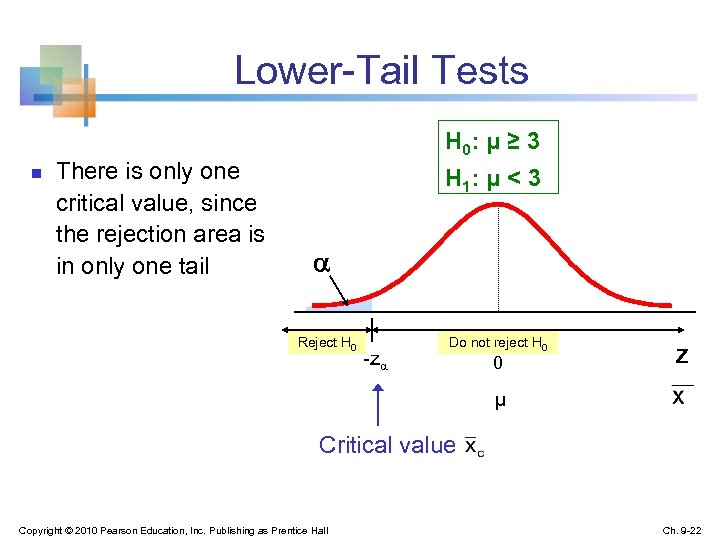
Lower-Tail Tests n There is only one critical value, since the rejection area is in only one tail H 0: μ ≥ 3 H 1: μ < 3 Reject H 0 -z Do not reject H 0 0 Z μ Critical value Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Ch. 9 -22
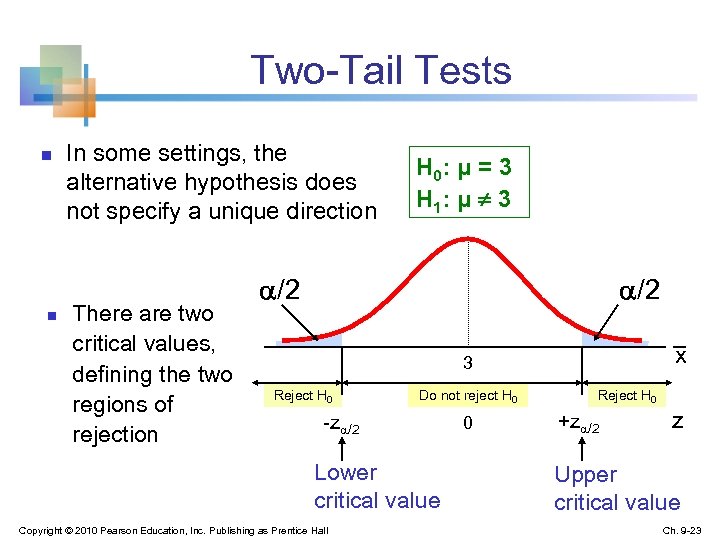
Two-Tail Tests n n In some settings, the alternative hypothesis does not specify a unique direction There are two critical values, defining the two regions of rejection H 0: μ = 3 H 1: μ ¹ 3 /2 x 3 Reject H 0 Do not reject H 0 -z /2 Lower critical value Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 0 Reject H 0 +z /2 z Upper critical value Ch. 9 -23

Example 9. 1 (B. p-336) Evaluating a new production process (hypothesis test: Upper tail Z test) n n n The production manager of Northern Windows Inc. has asked you to evaluate a proposed new procedure for producing its Regal line of double-hung windows. The present process has a mean production of 80 units per hour with a population standard deviation of σ = 8. the manager indicates that she does not want to change a new procedure unless there is strong evidence that the mean production level is higher with the new process. Assume n=25 and α=0. 05. Also assume that the sample mean was 83. What decision would you recommend based on hypothesis testing? Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -24

Example 9. 2 n n n Lower Tail Test The production manager of Twin Forks ball bearing has asked your assistance in evaluating a modified ball bearing production process. When the process is operating properly the process produces ball bearings whose weights are normally distributed with a population mean of 5 ounces and a population standard deviation of 0. 1 ounce. The sample mean was 4. 962 and n= 16. A new raw material supplier was used for a recent production run, and the manager wants to know if that change has resulted in lowering of the mean weight of bearings. What will be your conclusion for a lower tail test? Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -25

Example 9. 3 Two n n tailed test The production manager of Circuits Unlimited has asked for your assistance in analyzing a production process. The process involves drilling holes whose diameters are normally distributed with population mean 2 inches and population standard deviation 0. 06 inch. A random sample of nine measurements had a sample mean of 1. 95 inches. Use a significance level of 0. 05 to determine if the observed sample mean is unusual and suggests that the machine should be adjusted. Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -26

t Test of Hypothesis for the Mean (σ Unknown) n Convert sample result ( ) to a t test statistic Hypothesis Tests for σ Known σ Unknown Consider the test The decision rule is: (Assume the population is normal) Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -27

t Test of Hypothesis for the Mean (σ Unknown) (continued) n For a two-tailed test: Consider the test (Assume the population is normal, and the population variance is unknown) The decision rule is: Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -28

Example 2: Two-Tail Test ( Unknown) The average cost of a hotel room in New York is said to be $168 per night. A random sample of 25 hotels resulted in x = $172. 50 and s = $15. 40. Test at the = 0. 05 level. H 0: μ = 168 H 1: μ ¹ 168 (Assume the population distribution is normal) Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -29

Example Solution: Two-Tail Test H 0: μ = 168 H 1: μ ¹ 168 n = 0. 05 /2=. 025 Reject H 0 -t n-1, α/2 -2. 0639 n n = 25 n is unknown, so use a t statistic /2=. 025 Do not reject H 0 Reject H 0 0 1. 46 t n-1, α/2 2. 0639 n Critical Value: t 24 , . 025 = ± 2. 0639 Do not reject H 0: not sufficient evidence that true mean cost is different than $168 Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -30

Tests of the Population Proportion n Involves categorical variables n Two possible outcomes n n “Success” (a certain characteristic is present) “Failure” (the characteristic is not present) Fraction or proportion of the population in the “success” category is denoted by P Assume sample size is large Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -31

Proportions (continued) n Sample proportion in the success category is denoted by n n When n. P(1 – P) > 9, can be approximated by a normal distribution with mean and standard deviation n Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -32

Hypothesis Tests for Proportions n The sampling distribution of is Hypothesis approximately Tests for P normal, so the test statistic is a z n. P(1 – P) < 9 n. P(1 – P) > 9 value: Not discussed in this chapter Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -33

Example 3: Z Test for Proportion A marketing company claims that it receives 8% responses from its mailing. To test this claim, a random sample of 500 were surveyed with 25 responses. Test at the =. 05 significance level. Check: Our approximation for P is = 25/500 =. 05 n. P(1 - P) = (500)(. 05)(. 95) = 23. 75 > 9 Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -34

Z Test for Proportion: Solution Test Statistic: H 0: P =. 08 H 1: P ¹. 08 =. 05 n = 500, =. 05 Decision: Critical Values: ± 1. 96 Reject . 025 -1. 96 0 1. 96 z -2. 47 Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Reject H 0 at =. 05 Conclusion: There is sufficient evidence to reject the company’s claim of 8% response rate. Chap 10 -35

Two Procedures Two procedures to make tests of hypothesis 1. The p-value approach 2. The critical-value approach Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

p-Value Approach to Testing n p-value: Probability of obtaining a test statistic more extreme ( ≤ or ) than the observed sample value given H 0 is true n n n Also called observed level of significance Smallest value of for which H 0 can be rejected Decision rule: compare the p-value to n If p-value < , reject H 0 n If p-value , do not reject H 0 Statistics for Business and Economics, 6 e © 2007 Pearson Education, Inc. Chap 10 -37

HYPOTHESIS TESTS ABOUT μ: σ KNOWN Definition Assuming that the null hypothesis is true, the p-value can be defined as the probability that a sample statistic (such as the sample mean) is at least as far away from the hypothesized value in the direction of the alternative hypothesis as the one obtained from the sample data under consideration. Note that the p–value is the smallest significance level at which the null hypothesis is rejected. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved
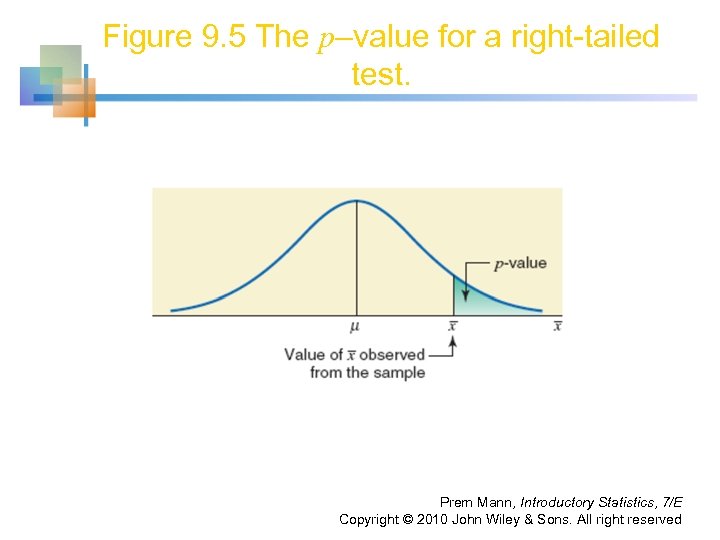
Figure 9. 5 The p–value for a right-tailed test. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved
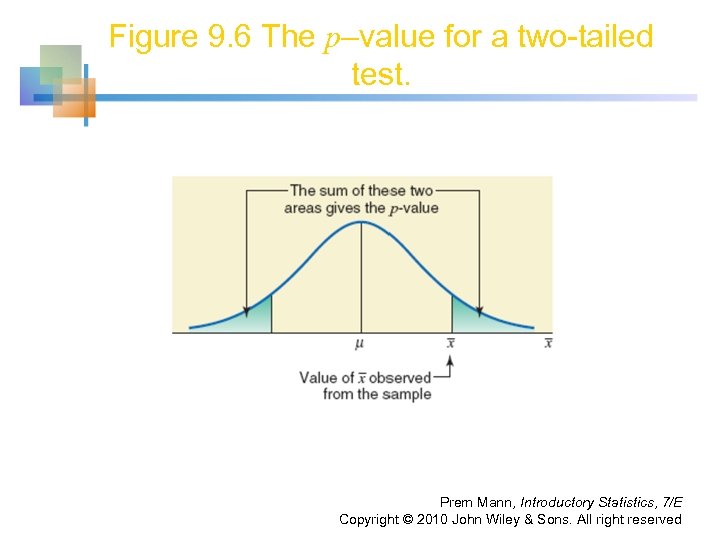
Figure 9. 6 The p–value for a two-tailed test. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Calculating the z Value for x When using the normal distribution, the value of z for x for a test of hypothesis about μ is computed as follows: The value of z calculated for x using this formula is also called the observed value of z. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Steps to Perform a Test of Hypothesis Using the p–Value Approach 1. 2. 3. 4. State the null and alternative hypothesis. Select the distribution to use. Calculate the p–value. Make a decision. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 9 -1 (p–Value Approach) At Canon Food Corporation, it used to take an average of 90 minutes for new workers to learn a food processing job. Recently the company installed a new food processing machine. The supervisor at the company wants to find if the mean time taken by new workers to learn the food processing procedure on this new machine is different from 90 minutes. A sample of 20 workers showed that it took, on average, 85 minutes for them to learn the food processing procedure on the new machine. It is known that the learning times for all new workers are normally distributed with a population standard deviation of 7 minutes. Find the p–value for the test that the mean learning time for the food processing procedure on the new machine is different from 90 minutes. What will your conclusion be if α =. 01? Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 9 -1: Solution § Step 1: H 0: μ = 90 H 1: μ ≠ 90 § Step 2: The population standard deviation σ is known, the sample size is small (n < 30), but the population distribution is normal. We will use the normal distribution to find the p–value and make the test. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 9 -1: Solution § Step 3: see 3. 19 from z table, we find. 9993 so 1 -. 9993= 0. 0007 p-value = 2(. 0007) =. 0014 Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved
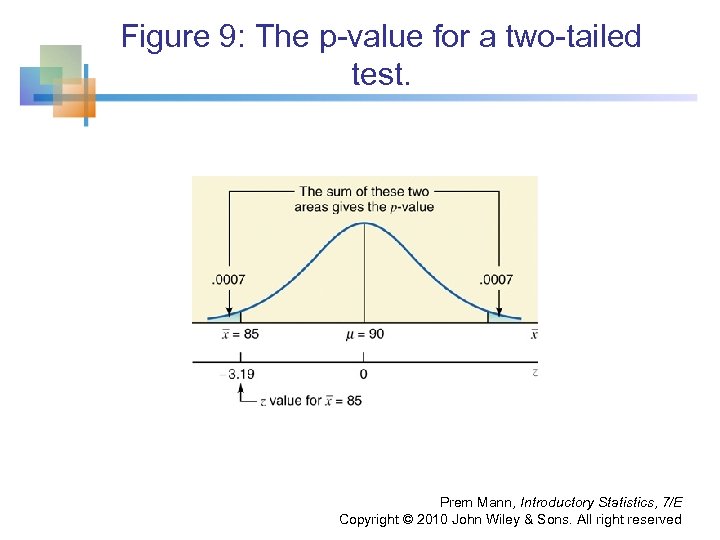
Figure 9: The p-value for a two-tailed test. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved

Example 9 -1: Solution § Step 4: Because α =. 01 is greater than the p- value of. 0014, we reject the null hypothesis at this significance level. Therefore, we conclude that the mean time for learning the food processing procedure on the new machine is different from 90 minutes. Prem Mann, Introductory Statistics, 7/E Copyright © 2010 John Wiley & Sons. All right reserved
836c44b96f094460ddc4b676775e626e.ppt