STATISTICS 542 Introduction to Clinical Trials RANDOMIZATION METHODS

STATISTICS 542 Introduction to Clinical Trials RANDOMIZATION METHODS 1

RANDOMIZATION • Why randomize • What a random series is • How to randomize 2

Randomization (1) • Rationale • Reference: Byar et al (1976) NEJM 274: 74 -80. • Best way to find out which therapy is best • Reduce risk of current and future patients of being on harmful treatment • Example: Retrolental Fibroplasia (Silverman: Scientific American 236: 100 -107, 1977) 3

Randomization (2) Basic Benefits of Randomization • Eliminates assignment basis • Tends to produce comparable groups • Produces valid statistical tests Basic Methods Ref: Zelen JCD 27: 365 -375, 1974. Pocock Biometrics 35: 183 -197, 1979 4

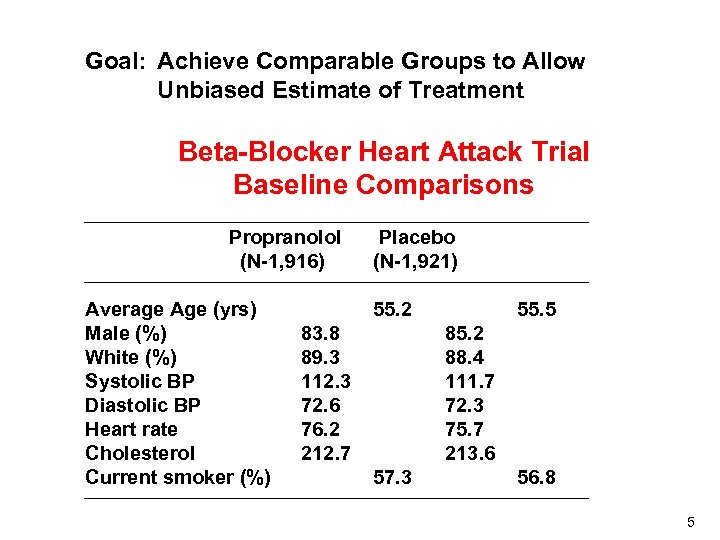Goal: Achieve Comparable Groups to Allow Unbiased Estimate of Treatment Beta-Blocker Heart Attack Trial Baseline Comparisons Propranolol (N-1, 916) Average Age (yrs) Male (%) White (%) Systolic BP Diastolic BP Heart rate Cholesterol Current smoker (%) Placebo (N-1, 921) 55. 2 83. 8 89. 3 112. 3 72. 6 76. 2 212. 7 55. 5 85. 2 88. 4 111. 7 72. 3 75. 7 213. 6 57. 3 56. 8 5

Randomization Basis for Tests of Hypotheses • The use of randomization provides a basis for an assumption-free statistical test of the equality of treatments • Such tests were originally proposed by Fisher and are known as randomization or permutation tests • With sample sizes na and nb , the conditional reference set Wc consists of n choose na possible combinations of na patients on treatment a out of n patients 6

Statistical Properties of Randomization A. Sampling-Based Population Model Population a y~G(y| a) Population b y~G(y| b) Sample at Random na patients nb patients yaj~G(y| a) B. Randomization Model ybj~G(y| b) Study Sample n = nb + nb patients Randomization na patients nb patients 7

Randomization Model • Under H 0, observed responses independent of treatment Observed group differences depends ONLY on sequence of n assignments (random). • Conditional Reference Set Sc Sc = n. Cna possible combinations, given na out of n • How many ways could na of the outcomes be assigned to treatment group A? • Permutation tests usually based on Sc, conditional reference set. • Under simple randomization, permutation test is asymptotically equal to homogeneous population model test. 8

Nature of Random Numbers and Randomness • A completely random sequence of digits is a mathematical idealization • Each digit occurs equally frequently in the whole sequence • Adjacent (set of) digits are completely independent of one another • Moderately long sections of the whole show substantial regularity • A table of random digits • Produced by a process which will give results closely approximating to the mathematical idealization • Tested to check that it behaves as a finite section from a completely random series should • Randomness is a property of the table as a whole • Different numbers in the table are independent 9

Table of Random Numbers 10

Allocation Procedures to Achieve Balance • Simple randomization • Biased coin randomization • Permuted block randomization • Balanced permuted block randomization • Stratified randomization • Minimization method 11

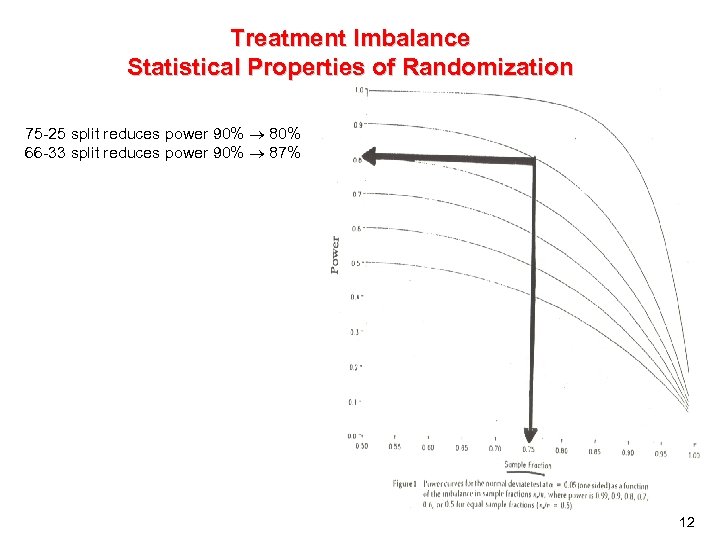Treatment Imbalance Statistical Properties of Randomization 75 -25 split reduces power 90% 80% 66 -33 split reduces power 90% 87% 12

Randomization & Balance (1) n = 100 p=½ s = #heads V(s) = npq = 100 · ½ = 25 E(s) = n · p = 50 13

Randomization & Balance (2) n = 20 p=½ E(s) = 10 V(s) = np = 20/4 = 5 14

Simple Random Allocation A specified probability, usually equal, of patients assigned to each treatment arm, remains constant or may change but not a function of covariates or response a. Fixed Random Allocation • n known in advance, exactly • n/2 selected at random & assigned to Trt A, rest to Trt B b. Complete Randomization (most common) • n not exactly known • marginal and conditional probability of assignment = 1/2 • analogous to a coin flip (random digits) 15

Simple Randomization • Advantage: simple and easy to implement • Disadvantage: At any point in time, there may be an imbalance in the number of subjects on each treatment • With n = 20 on two treatments A and B, the chance of a 12: 8 split or worse is approximately 0. 5 • With n = 100, the chance of a 60: 40 split or worse is approximately 0. 025 • Balance improves as the sample size n increases • Thus desirable to restrict randomization to ensure balance throughout the trial 16

Restricted Randomization • Simple randomization does not guarantee balance over time in each realization • Patient characteristics can change during recruitment (e. g. early pts sicker than later) • Restricted randomizations guarantee balance 1. Permuted-block 2. Biased coin (Efron) 3. Urn design (LJ Wei) 17

Permuted-Block Randomization (1) • Simple randomization does not guarantee balance in numbers during trial – If patient characteristics change with time, early imbalances – can't be corrected – Need to avoid runs in Trt assignment • Permuted Block insures balance over time • Basic Idea – – – Divide potential patients into B groups or blocks of size 2 m Randomize each block such that m patients are allocated to A and m to B Total sample size of 2 m B For each block, there are 2 m. Cm possible realizations (assuming 2 treatments, A & B) Maximum imbalance at any time = 2 m/2 = m 18

Permuted-Block Randomization (2) Method 1: Example • Block size 2 m = 4 2 Trts A, B } 4 C 2 = 6 possible • Write down all possible assignments • For each block, randomly choose one of the six possible arrangements • {AABB, ABAB, BABA, BBAA, ABBA} ABAB Pts 1234 BABA 5678 . . . 9 10 11 12 19

Permuted-Block Randomization (3) • Method 2: In each block, generate a uniform random number for each treatment (Trt), then rank the treatments in order Trt in any order Random Number A A B B Rank 0. 07 0. 73 0. 87 B Trt in rank 1 3 4 0. 31 A B A 2 20

Permuted-Block Randomization (4) • Concerns - If blocking is not masked, the sequence become somewhat predictable (e. g. 2 m = 4) ABAB BAB? Must be A. AA Must be B B. - This could lead to selection bias • Simple Solution to Selection Bias * Do not reveal blocking mechanism * Use random block sizes • If treatment is double blind, no selection bias 21

Biased Coin Design (BCD) Efron (1971) Biometrika • • • Allocation probability to Treatment A changes to keep balance in each group nearly equal BCD (p) – Assume two treatments A & B – D = n. A -n. B "running difference" n = n. A + n. B – Define p = prob of assigning Trt > 1/2 – e. g. PA = prob of assigning Trt A If D = 0, PA = 1/2 D > 0, PA = 1 - p Excess A's D < 0, PA = p Excess B's Efron suggests p=2/3 D > 0 PA = 1/3 D < 0 PA = 2/3 22

Urn Randomization Wei & Lachin: Controlled Clinical Trials, 1988 • A generalization of Biased Coin Designs • BCD correction probability (e. g. 2/3) remains constant regardless of the degree of imbalance • Urn design modifies p as a function of the degree of imbalance • U( , ) & two Trts (A, B) – 0. Urn with white, red balls to start – 1. Ball is drawn at random & replaced – 2. If red, assign B If white, assign A – 3. Add balls of opposite color (e. g. If red, add white) – 4. Go to 1. • Permutational tests are available, but software not as easy. 23

Analysis & Inference • Most analyses do not incorporate blocking • Need to consider effects of ignoring blocks – Actually, most important question is whether we should use complete randomization and take a chance of imbalance or use permuted-block and ignore blocks • Homogeneous or Heterogeneous Time Pop. Model – Homogeneous in Time • Blocking probably not needed, but if blocking ignored, no problem – Heterogeneoous in Time • Blocking useful, intrablock correlations induced • Ignoring blocking most likely conservative • Model based inferences not affected by treatment allocation scheme. Ref: Begg & Kalish (Biometrics, 1984) 24

Kalish & Begg Controlled Clinical Trials, 1985 Time Trend – Impact of typical time trends (based on ECOG pts) on nominal p-values likely to be negligible – A very strong time trend can have non-negligible effect on p-value – If time trends cause a wide range of response rates, adjust for time strata as a co-variate. This variation likely to be noticed during interim analysis. 25

Balancing on Baseline Covariates • Stratified Randomization • Covariate Adaptive – Minimization – Pocock & Simon 26

Stratified Randomization (1) • May desire to have treatment groups balanced with respect to prognostic or risk factors (co-variates) • For large studies, randomization “tends” to give balance • For smaller studies a better guarantee may be needed • Divide each risk factor into discrete categories Number of strata f = # risk factors; li = number of categories in factor i • Randomize within each stratum • For stratified randomization, randomization must be restricted! Otherwise, (if CRD was used), no balance is guaranteed despite the effort. 27

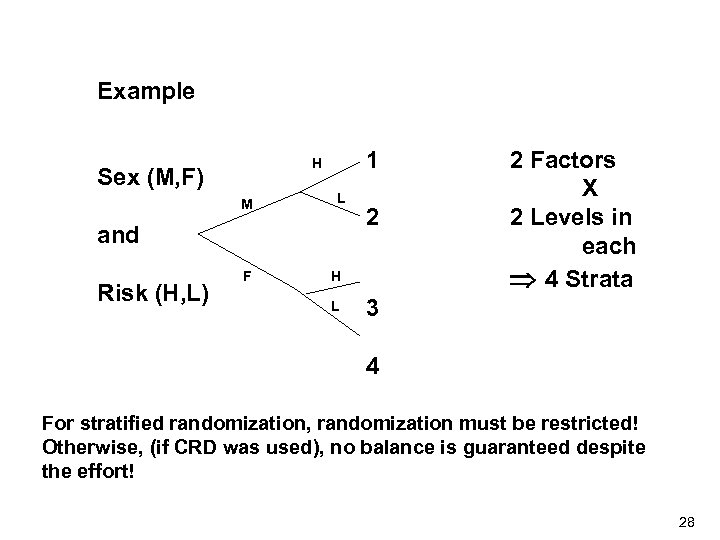Example 1 H Sex (M, F) M L F H and Risk (H, L) L 2 2 Factors X 2 Levels in each 4 Strata 3 4 For stratified randomization, randomization must be restricted! Otherwise, (if CRD was used), no balance is guaranteed despite the effort! 28

Stratified Randomization (2) • Define strata • Randomization is performed within each stratum and is usually blocked • Example: Age, < 40, 41 -60, >60; Sex, M, F Total number of strata = 3 x 2 = 6 Age Male Female 40 41 -60 >60 ABBA, BAAB, … BBAA, ABAB, . . . AABB, ABBA, . . . BABA, BAAB, . . . ABAB, BBAA, . . . BAAB, ABAB, . . 29

Stratified Randomization (3) • The block size should be relative small to maintain balance in small strata, and to insure that the overall imbalance is not too great • With several strata, predictability should not be a problem • Increased number of stratification variables or increased number of levels within strata lead to fewer patients per stratum • In small sample size studies, sparse data in many cells defeats the purpose of stratification • Stratification factors should be used in the analysis • Otherwise, the overall test will be conservative 30

Comment • For multicenter trials, clinic should be a factor Gives replication of “same” experiment. • Strictly speaking, analysis should take the particular randomization process into account; usually ignored (especially blocking) & thereby losing some sensitivity. • Stratification can be used only to a limited extent, especially for small trials where it's the most useful; i. e. many empty or partly filled strata. • If stratification is used, restricted randomization within strata must be used. 31

Minimization Method (1) • An attempt to resolve the problem of empty strata when trying to balance on many factors with a small number of subjects • Balances Trt assignment simultaneously over many strata • Used when the number of strata is large relative to sample size as stratified randomization would yield sparse strata • A multiple risk factors need to be incorporated into a score for degree of imbalance • Need to keep a running total of allocation by strata • Also known as the dynamic allocation • Logistically more complicated • Does not balance within cross-classified stratum cells; balances over the marginal totals of each stratum, separately 32

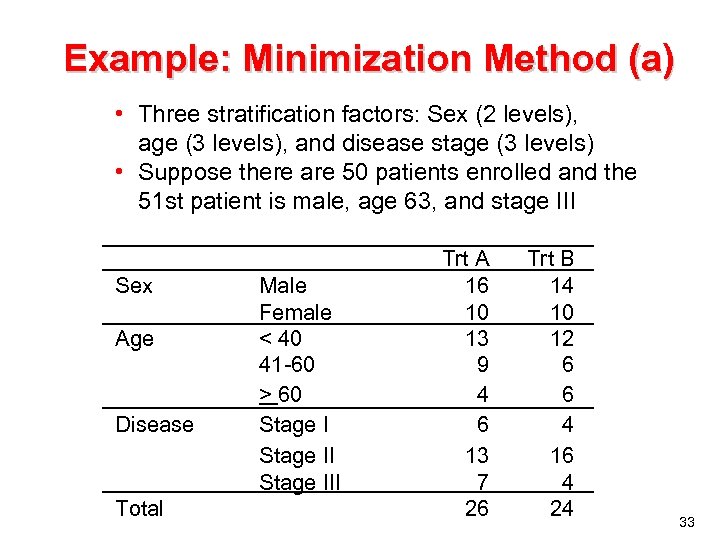Example: Minimization Method (a) • Three stratification factors: Sex (2 levels), age (3 levels), and disease stage (3 levels) • Suppose there are 50 patients enrolled and the 51 st patient is male, age 63, and stage III Sex Age Disease Total Male Female < 40 41 -60 > 60 Stage III Trt A 16 10 13 9 4 6 13 7 26 Trt B 14 10 12 6 6 4 16 4 24 33

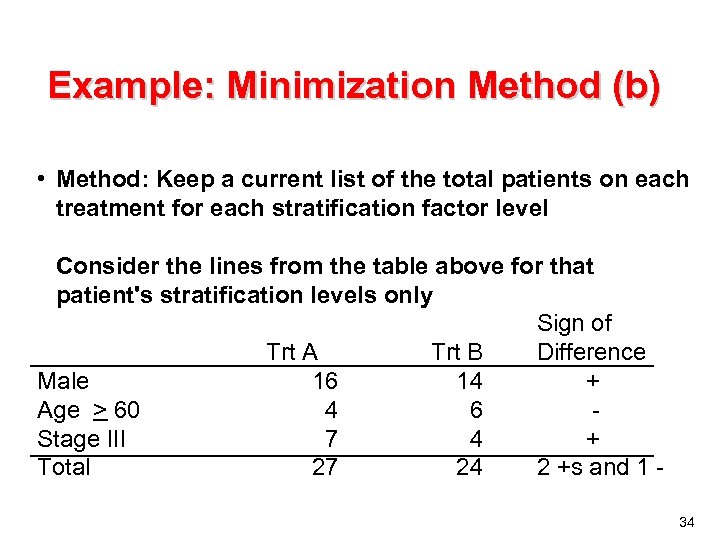Example: Minimization Method (b) • Method: Keep a current list of the total patients on each treatment for each stratification factor level Consider the lines from the table above for that patient's stratification levels only Sign of Trt A Trt B Difference Male 16 14 + Age > 60 4 6 Stage III 7 4 + Total 27 24 2 +s and 1 34

Example: Minimization Method (c) • Two possible criteria: • Count only the direction (sign) of the difference in each category. Trt A is “ahead” in two categories out of three, so assign the patient to Trt B • Add the total overall categories (27 As vs 24 Bs). Since Trt A is “ahead, ” assign the patient to Trt B 35

Minimization Method (2) • These two criteria will usually agree, but not always • Choose one of the two criteria to be used for the entire study • Both criteria will lead to reasonable balance • When there is a tie, use simple randomization • Generalization is possible • Balance by margins does not guarantee overall treatment balance, or balance within stratum cells 36

Covariate Adaptive Allocation (Sequential Balanced Stratification) Pocock & Simon, Biometrics, 1975; Efron, Biometrika, 1971 • Goal is to balance on a number of factors but with "small" numbers of subjects • In a simple case, if at some point Trt A has more older patients that Trt B, next few older patients should more likely be given Trt B until "balance" is achieved • Several risk factors can be incorporated into a score for degree of imbalance B(t) for placing next patient on treatment t (A or B) • Place patient on treatment with probability p > 1/2 which causes the smallest B(t), or the least imbalance • More complicated to implement - usually requires a small "desk top" computer 37

Example: Baseline Adaptive Randomization • Assume 2 treatments (1 & 2) 2 prognostic factors (1 & 2) (Gender & Risk Group) Factor 1 - 2 levels (M & F) Factor 2 - 3 levels (High, Medium & Low Risk) Let B(t) = Wi Range (xit 1, xit 2) wi = weight for each factor e. g. w 1 = 3 w 1/w 2 = 1. 5 w 2 = 2 xij = number of patients in ith factor and jth treatment xitj = change in xij if next patient assigned treatment t • Let P = 2/3 for smallest B(t) Pi = (2/3, 1/3) • Assume we have already randomized 50 patients • Now 51 st pt. Male (1 st level, factor 1) Low Risk (3 rd level, factor 2) 38

Now determine B(1) and B(2) for patient #51. … • If assigned Treatment 1 (t = 1) (a) Calculate B(t) (Assign Pt #51 to trt 1) t = 1 (1) Factor 1, Level 1 (Male) Trt Group K 1 2 Now Proposed X 1 K X 11 K 16 17 14 14 Range =|17 -14| = 3 39

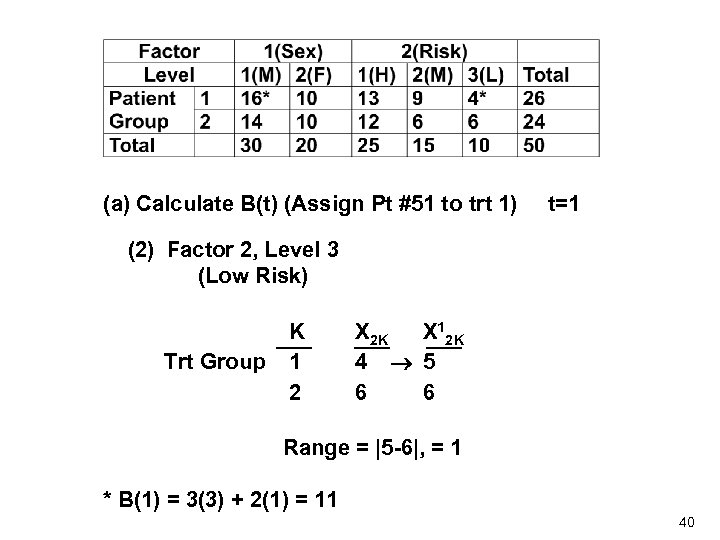(a) Calculate B(t) (Assign Pt #51 to trt 1) t=1 (2) Factor 2, Level 3 (Low Risk) Trt Group K 1 2 X 2 K X 12 K 4 5 6 6 Range = |5 -6|, = 1 * B(1) = 3(3) + 2(1) = 11 40

(b) Calculate B(2) (Assign Pt #51 to trt 2) t=2 (1) Factor 1, Level 1 (Male) K X 1 K X 21 K Group 1 16 16 2 14 15 Range = |16 -15| = 1 (2) Factor 2, Level 3 (Low Risk) K X 2 k X 22 k Group 1 4 4 2 6 7 Range = |4 -7| = 3 * B(2) = 3(1) + 2(3) = 9 41

(c) Rank B(1) and B(2), measures of imbalance Assign t with probability t B(t) 2 9 2/3 1 11 1/3 * Note: “minimization” would assign treatment 2 for sure 42

Response Adaptive Allocation Procedures • Use outcome data obtained during trial to influence allocation of patient to treatment • Data-driven i. e. dependent on outcome of previous patients • Assumes patient response known before next patient • The goal is to allocate as few patients as possible to a seemingly inferior treatment • Issues of proper analyses quite complicated • Not widely used though much written about • Very controversial 43

Play-the-Winner Rule Zelen (1969) • Treatment assignment depends on the outcome of previous patients • Response adaptive assignment • When response is determined quickly • 1 st subject: toss a coin, H = Trt A, T = Trt B • On subsequent subjects, assign previous treatment if it was successful • Otherwise, switch treatment assignment for next patient • Advantage: Potentially more patients receive the better treatment • Disadvantage: Investigator knows the next assignment 44

Response Adaptive Randomization Example "Play-the-winner” Zelen (1969) JASA TRT B SSF SF Patient 1 2 3 4 5 6 7 8 9. . . 45

Two-armed Bandit or Randomized Play-the-Winner Rule • Treatment assignment probabilities depend on observed success probabilities at each time point • Example: ECMO trial • Advantage: Attempts to maximize the number of subjects on the “superior” treatment • Disadvantage: When unequal treatment numbers result, there is loss of statistical power in the treatment comparison 46

ECMO Example • References Michigan 1 a. Bartlett R. , Roloff D. , et al. ; Pediatrics (1985) 1 b. Begg C. ; Biometrika (1990) Harvard 2 a. O’Rourke P. , Crone R. , et al. ; Pediatrics (1989) 2 b. Ware J. ; Statistical Science (1989) 2 c. Royall R. ; Statistical Science (1991) • Extracoporeal Membrane Oxygenator(ECMO) – treat newborn infants with respiratory failure or hypertension – ECMO vs. conventional care 47

Michigan ECMO Trial • Bartlett Pediatrics (1985) • Modified “play-the-winner” – Urn model A ball ECMO B ball Standard control If success on A, add another A ball. … – Wei & Durham JASA (1978) • Randomized Consent Design • Results *sickest patient • P-Values, depending on method, values ranged. 001 6. 05 6. 28 48

Harvard ECMO Trial (1) • O’Rourke, et al. ; Pediatrics (1989) • ECMO for pulmonary hypertension • Background – Controversy of Michigan Trial – Harvard experience of standard 11/13 died • Randomized Consent Design – Two stage 1 st Randomization (permuted block) switch to superior treatment after 4 deaths in worst arm 2 nd Stay with best treatment 49

Harvard ECMO Trial (2) • Results Survival * less severe patients P =. 054 (Fisher) 50

Multi-institutional Trials • Often in multi-institutional trials, there is a marked institution effect on outcome measures • Using permuted blocks within strata, adding institution as yet another stratification factor will probably lead to sparse cells (and potentially more cells than patients!) • Use permuted block randomization balanced within institutions • Or use the minimization method, using institution as a stratification factor 51

Mechanics of Randomization (1) Basic Principle - “Analyze What is Randomized” * Timing • Actual randomization should be delayed until just prior to initiation of therapy • Example Alprenolol Trial, Ahlmark et al (1976) – 393 patients randomized two weeks before therapy – Only 162 patients treated, 69 alprenolol & 93 placebo 52

Mechanics of Randomization (2) * Operational 1. Sequenced sealed envelopes (prone to tampering!) 2. Sequenced bottles/packets 3. Phone call to central location - Live response - Voice Response System 4. One site PC system 5. Web based Best plans can easily be messed up in the implementation 53

Example of Previous Methods (1) 20 subjects, treatment A or B, risk H or L Subject Risk 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 pts on A 17 18 19 20 H L L L L H H H H L L H H L H Randomize Using 1. Simple 2. Blocked (Size=4) 3. Stratify by risk + use simple 4. Stratify by risk + block For each compute 1. Percent pts on A 2. For each risk group, percent of 10 subjects with H 10 subjects with L 54

Example of Previous Methods (2) 1. Simple (a) (b) 1 st Try 9/20 A's H: 5/10 A's L: 4/10 A's 2 nd Try 7/20 A's OVERALL BY 3/10 A's SUBGROUP 4/10 A's 2. Blocked (No stratification) (a) 10 A's & 10 B's (b) H: 4 A's & 6 B's L: 6 A's & 4 B's 3. Stratified with simple randomization (a) 5 A's & 15 B's (b) H: 1 A & 9 B's L: 4 A's & 6 B's 4. Stratified with blocking (a) 10 A's & 10 B's (b) MUST BLOCK TO MAKE STRATIFICATION PAY H: 5 A's & 5 B's OFF L: 5 A's & 5 B's 55