KL-Lec8.ppt
- Количество слайдов: 45

СТАТИСТИЧНІ МОДЕЛІ ДЛЯ ОБРОБКИ ПРИРОДНОЇ МОВИ ПРИХОВАНА МОДЕЛЬ МАРКОВА (НММ) ЛЕКЦІЯ № 8

ЛАНЦЮГ МАРКОВА ЗВАЖЕНИЙ СКІНЧЕННИЙ АВТОМАТ – АВТОМАТ З ДОДАНИМ ДО ДУГ ІМОВІРНОСТЯМИ ◦ СУМА ВСІХ ІМОВІРНОСТЕЙ , ЯКІ ВИХОДЯТЬ З ВУЗЛА ПОВИННА ДОРІВНЮВАТИ ОДИНИЦІ ЛАНЦЮГ МАРКОВА ОКРЕМИЙ ВИПАДОК ЗВАЖЕНОГО СКІНЧЕННОГО АВТОМАТУ В ЯКОМУ ВХІДНА ПОСЛІДОВНІСТЬ УНІКАЛЬНО ВИЗНАЧАЄ, ЯКІ СТАНИ ПРОЙДЕ АВТОМАТ ПРОБЛЕМУ НЕОДНОЗНАЧНОСТІ ЛАНЦЮГИ МАРКОВА ПРЕДСТАВИТИ НЕ МОДУТЬ. ◦ ВИКОРИСТОВУЮТЬСЯ ДЛЯ ВИЗНАЧЕННЯ ІМОВІРНОСТЕЙ ОДНОЗНАЧНИХ ПОСЛІДОВНОСТЕЙ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 2
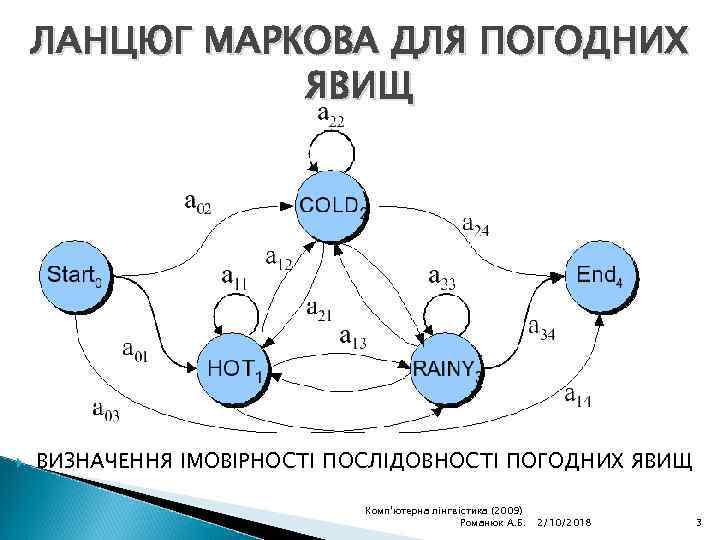
ЛАНЦЮГ МАРКОВА ДЛЯ ПОГОДНИХ ЯВИЩ ВИЗНАЧЕННЯ ІМОВІРНОСТІ ПОСЛІДОВНОСТІ ПОГОДНИХ ЯВИЩ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 3
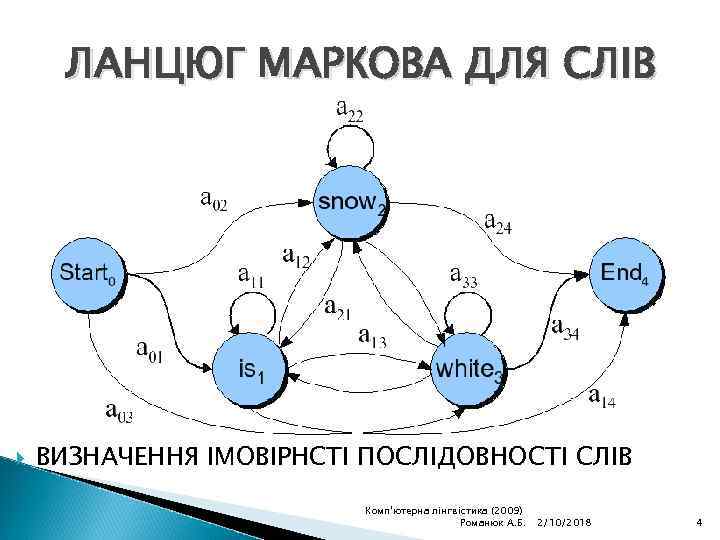
ЛАНЦЮГ МАРКОВА ДЛЯ СЛІВ ВИЗНАЧЕННЯ ІМОВІРНСТІ ПОСЛІДОВНОСТІ СЛІВ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 4

ЛАНЦЮГ МАРКОВА (ВИЗНАЧЕННЯ) Q = q 1, q 2…q. N A = a 01 a 02…an 1…ann q 0, q F НАБІР N CТАНІВ. СТАН В МОМЕНТ ЧАСУ t - qt МАТРИЦЯ ПЕРЕХІДНИХ ІМОВІРНОСТЕЙ, КОЖНЕ aij ПРЕДСТАВЛЯЄ ІМОВІРНІСТЬ ПЕРЕХОДУ ЗІ СТАНУ i В СТАН j. СПЕЦІАЛЬНИЙ ПОЧАТКОВИЙ СТАН ТА КІНЦЕВИЙ СТАН ЛАНЦЮГ МАРКОВА ПЕРШОГО ПОРЯДКУ – ІМОВІРНІСТЬ ПОТОЧНОГО СТАНУ ЗАЛЕЖИТЬ ТІЛЬКИ ВІД ПОПЕРЕДНЬОГО СТАНУ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 5

ЛАНЦЮГ МАРКОВА ДЛЯ ПОГОДНИХ ЯВИЩ ЯКА ІМОВІРНІСТЬ ЧОТИРЬОХ ГАРЯЧИХ ДНІВ? ПОСЛІДОВНІСТЬ ПОДІЙ: HOT, HOT ПОСЛІДОВНІСТЬ СТАНІВ: 1, 1, 1, 1 P(1, 1, 1, 1) = ◦ a 01 a 11 a 11 Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 6

ПРИХОВАНА МОДЕЛЬ МАРКОВА (ВИЗНАЧЕННЯ) Q = q 1, q 2…q. N НАБІР N СТАНІВ O= o 1, o 2…o. T ПОСЛІДОВНІСТЬ T СПОСТЕРЕЖЕНЬ. КОЖНЕ СПОСТЕРЕЖЕННЯ ЦЕ СИМВОЛ З НАБОРУ V = {v 1, v 2, …v. V} A = {aij} B=bi(OT) q 0 , q F МАТРИЦЯ ПЕРЕХІДНИХ ІМОВІРНОСТЕЙ. КОЖЕН ЕЛЕМЕНТ МАТРИЦІ ПРЕДСТАВЛЯЄ ІМОВІРНІСТЬ ПЕРЕХОДУ ЗІ СТАНУ i В СТАН j ПОСЛІДОВНІСТЬ ФУНКЦІЙ ПРАВДОПОДІБНОСТІ СПОСТЕРЕЖЕНЬ. ІМОВІРНОСТІ, ЩО СПОСТЕРЕЖЕННЯ o. T ГЕНЕРУЄТЬСЯ ЗІ СТАНУ i СПЕЦІАЛЬНИЙ ПОЧАТКОВИЙ І КІНЦЕВИЙ СТАНИ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 7

ПРИХОВАНА МОДЕЛЬ МАРКОВА В ЛАНЦЮГУ МАРКОВА СПОСТЕРЕЖЕННЯ І СТАНИ СПІВПАДАЮТЬ ПОГОДА – HOT, СТАН – HOT АМА – СПОСТЕРЕЖЕННЯ, ЦЕ СЛОВА А ПРИХОВАНІ СТАНИ, ЦЕ ТЕГИ ПРИХОВАНА МОДЕЛЬ МАРКОВА ЦЕ РОЗШИРЕННЯ ЛАНЦЮГА МАРКОВА В ЯКОМУ СПОСТЕРЕЖЕННЯ НЕ Є СТАНАМИ СТАН В ЯКОМУ МИ ЗНАХОДИМСЯ Є НЕВІДОМИМ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 8

ПРИКЛАД HMM (ПММ) ВИ КЛІМАТОЛОГ В 2799 р. ВИВЧАЄТЕ ПРОЦЕС ГЛОБАЛЬНОГО ПОТЕПЛІННЯ. ЗАПИСИ ПРО ПОГОДУ ЛІТОМ 2009 ВІДСУТНІ ЗНАЙДЕНО ЩОДЕННИК, В ЯКОМУ АВТОР, ЗАЗНАЧИВ СКІЛЬКИ ПОРЦІЙ МОРОЗИВА ВІД ЗЇДАВ, У ДЕНЬ, ПРОТЯГОМ УСЬОГО ЛІТА 2009. ЗАДАЧА: ВИЗНАЧИТИ НАСКІЛЬКИ ГАРЯЧИМ БУЛО ЛІТО 2009. Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 9

ПРИКЛАД HMM (ПММ) МАЮЧИ ПОСЛІДОВНІСТЬ СПОСТЕРЕЖЕНЬ O, КОЖНЕ З ЯКИХ, ЦЕ ЧИСЛО, ЯКЕ ВІДПОВІДАЄ КІЛЬКОСТІ ПОРЦІЙ МОРОЗИВА ЗЇДЖЕНИХ ДАНОГО ДНЯ ВИЗНАЧИТИ ПРАВІЛЬНУ ПРИХОВАНУ ПОСЛІДОВНІСТЬ Q СТАНІВ ПОГОДИ (H ЧИ C), ЯКІ СПРИЧИНИЛИ ЗЇДАННЯ ТАКОЇ КІЛЬКОСТІ МОРОЗИВА Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 10
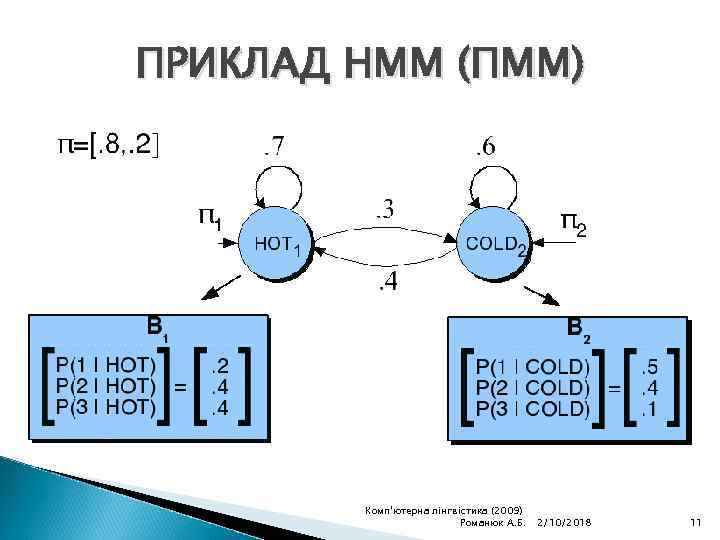
ПРИКЛАД HMM (ПММ) Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 11

ПРИПУЩЕННЯ HMM ІМОВІРНІСТЬ ПОТОЧНОГО СТАНУ ЗАЛЕЖИТЬ ТІЛЬКИ ВІД ПОПЕРЕДНЬОГО СТАНУ ІМОВІРНІСТЬ ВИХІДНОГО СПОСТЕРЕЖЕННЯ ЗАЛЕЖИТЬ ТІЛЬКИ ВІД СТАНУ, ЯКИЙ СПРИЧИНИВ ЦЕ СПОСТЕРЕЖЕННЯ І НЕ ЗАЛЕЖИТЬ ВІД ІНШИХ СПОСТЕРЕЖЕНЬ ТА ІНШИХ СТАНІВ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 12

ТРИ ОСНОВНІ ЗАДАЧІ НММ МАЮЧИ НММ, ДЛЯ ЗАДАНОЇ ПОСЛІДОВНОСТІ СПОСТЕРЕЖЕНЬ ВИЗНАЧИТИ ІМОВІРНІСТЬ ЦІЄЇ ПОСЛІДОВНОСТІ МАЮЧИ НММ, ДЛЯ ЗАДАНОЇ ПОСЛІДОВНОСТІ СПОСТЕРЕЖЕНЬ ВИЗНАЧИТИ НАЙКРАЩУ ПОСЛІДОВНІСТЬ ПРИХОВАНИХ СТАНІВ ДЛЯ ЗАДАНОЇ ПОСЛІДОВНОСТІ СПОСТЕРЕЖЕНЬ ТА НАБОРУ СТАНІВ ВИВЕСТИ ПАРАМЕТРИ НММ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 13

ЗАДАЧА 1. ВИЗНАЧЕННЯ ІМОВІРНОСТІ ПОСЛІДОВНОСТІ НММ ПОСЛІДОВНІСТЬ СПОСТЕРЕЖЕНЬ О ВИЗНАЧИТИ ІМОВІРНІСТЬ У ВИПАДКУ, КОЛИ СПОСТЕРЕЖЕННЯ СПІВПАДАЮТЬ З ПРИХОВАНИМИ ПОДІЯМИ (ЛАНЦЮГ МАРКОВА) ІМОВІРНІСТЬ ВИЗНАЧАЄТЬСЯ МНОЖЕННЯМ ІМОВІРНОСТЕЙ, ЯКІ ВІДПОВІДАЮТЬ ДУГАМ У ВИПАДКУ НММ, ПОТРІБНО ВИЗНАЧИТИ ІМОВІРНІСТЬ ПОСЛІДОВНОСТІ СПОСТЕРЕЖЕНЬ, ПРИ НЕВІДОМІЙ ПОСЛІДОВНОСТІ СТАНІВ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 14

ЗАДАЧА 1. ВИЗНАЧЕННЯ ІМОВІРНОСТІ ПОСЛІДОВНОСТІ ІМОВІРНІСТЬ ПОСЛІДОВНОСТІ СПОСТЕРЕЖЕНЬ ВІД ПЕВНОЇ ПОСЛІДОВНОСТІ ПРИХОВАНИХ СТАНІВ (НАПРИКЛАД ПОСЛІДОВНІСТЬ СПОСТЕРЕЖЕНЬ 3, 1, 3 ДЛЯ ОДНОЇ ПОСЛІДОВНОСТІ СТАНІВ HOT, COLD) Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 15

ЗАДАЧА 1. ВИЗНАЧЕННЯ ІМОВІРНОСТІ ПОСЛІДОВНОСТІ ЗАГАЛЬНА ІМОВІРНІСТЬ ПЕВНОЇ ПОСЛІДОВНОСТІ СТАНІВ, ЩО ГЕНЕРУЮТЬ ВІДПОВІДНУ ПОСЛІДОВНІСТЬ СПОСТЕРЕЖЕНЬ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 16

ЗАДАЧА 1. ВИЗНАЧЕННЯ ІМОВІРНОСТІ ПОСЛІДОВНОСТІ ПОВНА ІМОВІРНІСТЬ ПОТРЕБУЄ NT ОПЕРАЦІЙ АЛГОРИМ ПРЯМОГО ХОДУ ВИРІШУЄ ЗАДАЧУ ЗА N 2 T ОПЕРАЦІЙ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 17
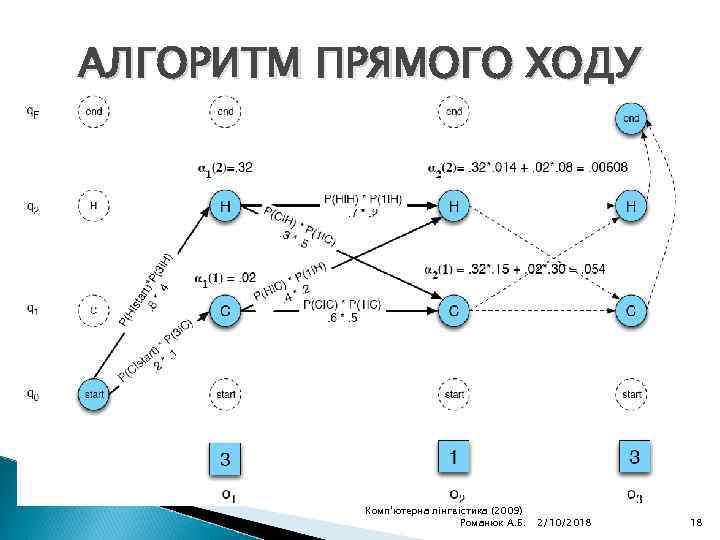
АЛГОРИТМ ПРЯМОГО ХОДУ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 18

АЛГОРИТМ ПРЯМОГО ХОДУ КОЖНА КОМІРКА ПРЕДСТАВЛЯЄ ІМОВІРНІСТЬ БУТИ В СТАНІ j ПІСЛЯ ПЕРШИХ t СПОСТЕРЕЖЕНЬ ЗНАЧЕННЯ ВИЗНАЧАЮТЬСЯ СУМУВАННЯМ ВСІХ ІМОВІРНОСТЕЙ ДЛЯ ШЛЯХІВ, ЯКІ ПРИВОДЯТЬ ДО ДАНОЇ КОМІРКИ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 19
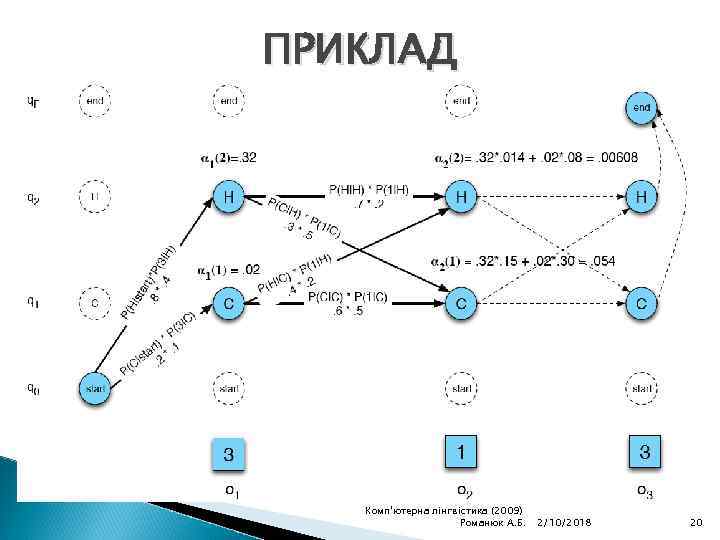
ПРИКЛАД Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 20
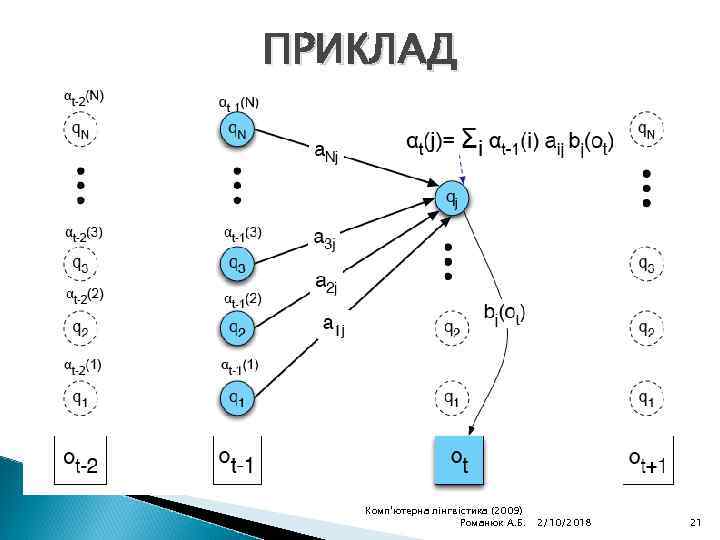
ПРИКЛАД Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 21

АЛГОРИТМ ПРЯМОГО ХОДУ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 22

ЗАДАЧА 2. ДЕКОДУВАННЯ. АЛГОРИТМ ВІТЕРБІ НММ ПОСЛІДОВНІСТЬ СПОСТЕРЕЖЕНЬ O= o 1, o 2…o. T ВИЗНАЧИТИ НАЙБІЛЬШ ІМОВІРНУ ПОСЛІДОВНІСТЬ СТАНІВ Q = q 1, q 2…q. Т Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 23

ЗАДАЧА 2. ДЕКОДУВАННЯ. АЛГОРИТМ ВІТЕРБІ КОЖНА КОМІРКА ПРЕДСТАВЛЯЄ ІМОВІРНІСТЬ ЩО НММ Є В СТАНІ j ПІСЛЯ ПЕРШИХ t СПОСТЕРЕЖЕНЬ І ПРОХОДЖЕННЯ НАЙБІЛЬШ ІМОВІРНОЇ ПОСЛІДОВНОСТІ СТАНІВ ЗНАЧЕННЯ ВИЗНАЧАЄТЬСЯ ОБЧИСЛЕННЯМ НАЙБІЛЬШ ІМОВІРНОГО ШЛЯХУ ДО ДАНОЇ КОМІРКИ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 24
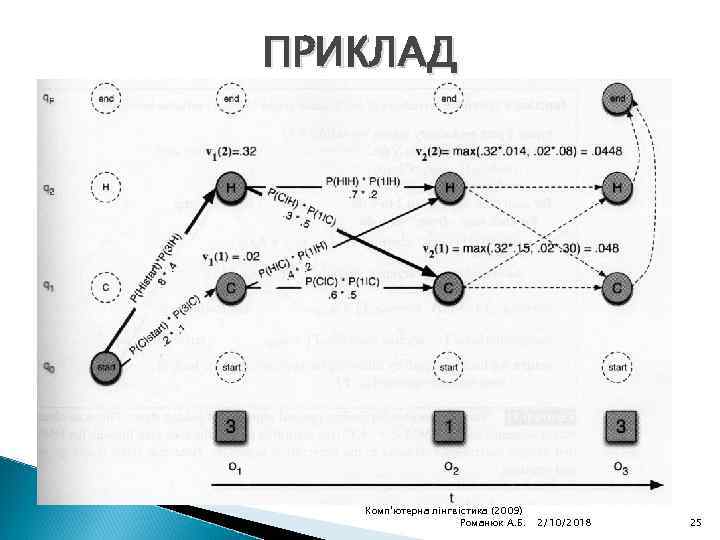
ПРИКЛАД Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 25

АЛГОРИТМ ВІТЕРБІ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 26
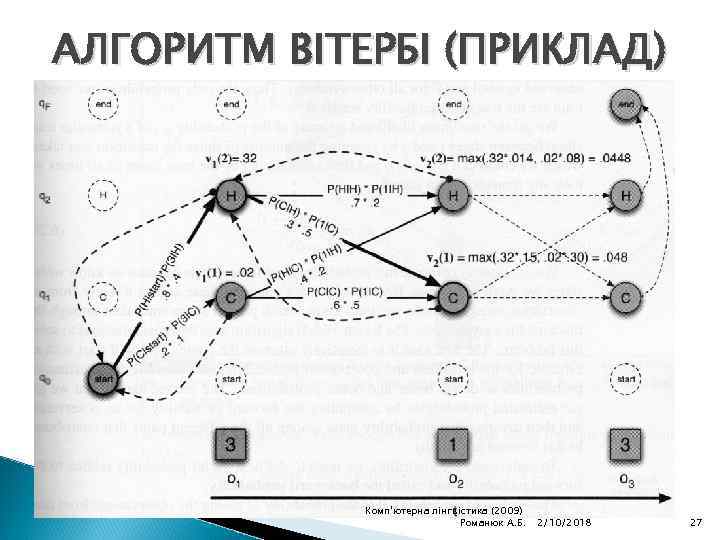
АЛГОРИТМ ВІТЕРБІ (ПРИКЛАД) Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 27

ТРЕНУВАННЯ НММ. АЛГОРИТМ “ВПЕРЕД - НАЗАД” ПОСЛІДОВНІСТЬ СПОСТЕРЕЖЕНЬ O НАБІР МОЖЛИВИХ СТАНІВ НММ Q ВИЗНАЧИТИ ПАРАМЕТРИ НММ (МАТРИЦЮ ПЕРЕХІДНИХ ІМОВІРНОСТЕЙ ТА МАТРИЦЮ ІМОВІРНОСТЕЙ СПОСТЕРЕЖЕНЬ) В ЗАДАЧІ ПРО МОРОЗИВО ◦ O = {1, 3, 2. , , , . } ◦ Q = {H, C} Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 28

ПОЧИНАЄМО ЗІ СПРОЩЕНОЇ МОДЕЛІ МАРКОВА (ЛАНЦЮГ МАРКОВА) ЗАПУСКАЄМО МОДЕЛЬ ДЛЯ ПОСЛІДОВНОСТІ СПОСТЕРЕЖЕНЬ O. ОСКІЛЬКИ ВОНИ НЕ Є ПРИХОВАНІ, ВИЗНАЧАЄМО СТАНИ, ЯКІ ГЕНЕРУЮТЬ ПОСЛІДОВНІСТЬ СПОСТЕРЕЖЕНЬ ТА ШЛЯХ ЧЕРЕЗ МОДЕЛЬ. МАЮЧИ ТАКУ ІНФОРМАЦІЮ ТРЕНУЄМО МОДЕЛЬ: ◦ B = {bk(ot)}: ОСКІЛЬКИ, КОЖЕН СТАН МОЖЕ ГЕНЕРУВАТИ ТІЛЬКИ ОДНЕ СПОСТЕРЕЖЕННЯ ВСІ ІМОВІРНОСТІ СПОСТЕРЕЖЕНЬ ДОРІВНЮЮТЬ 1. 0 ◦ A = {aij}: Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 29

ДЛЯ HMM, ОБЧИСЛИТИ ЦІ ЧИСЛА ПРЯМО ЧЕРЕЗ ПОСЛІДОВНОСТІ СПОСТЕРЕЖЕНЬ НЕМОЖЛИВО БАУМА-ВЕЛША ПРИПУЩЕННЯ: ◦ ІТЕРАЦІЙНЕ ОТРИМАННЯ РЕЗУЛЬТВТІВ. ПОЧИНАЄМО З ПЕВНИХ ЗНАЧЕНЬ aij ТА bk, І ІТЕРАЦІЙНО ЇХ ПОКРАЩУЄМО ◦ ПОКРАЩЕНІ ІМОВІРНОСТІ: ОБЧИСЛИТИ ПРЯМІ ІМОВІРНОСТІ ДЛЯ ВСІХ СПОСТЕРЕЖЕНЬ РОЗДІЛИТИ ЦІ ІМОВІРНОСТІ ДЛЯ РІЗНИХ ШЛЯХІВ , ЯКІ ПРИВОДЯТЬ ДО ЦИХ ПРЯМИХ ІМОВІРНОСТЕЙ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 30

АЛГОРИТМ ЗВОРОТНЬОГО ХОДУ ВИЗНАЧИМО ЗВОРОТНУ ІМОВІРНІСТЬ ЯК: ЦЕ Є ІМОВІРНІСТЬ ГЕНЕРАЦІЇ ПЕВНИХ СПОСТЕРЕЖЕНЬ Ot+1 T З МОМЕНТУ ЧАСУ t+1 ДО ЗАВЕРШЕННЯ, ПРИ УМОВІ ЩО HMM Є В СТАНІ i В МОМЕНТ ЧАСУ t ТА ЗВИЧАЙНО ЗАДАНА САМА НММ. Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 31

Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 32
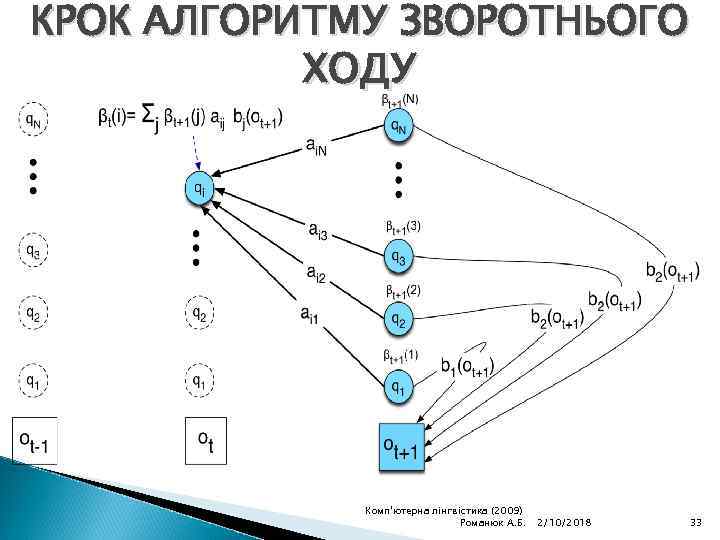
КРОК АЛГОРИТМУ ЗВОРОТНЬОГО ХОДУ Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 33

ПЕРЕВИЗНАЧЕННЯ aij ПРИБЛИЗНЕ ВИЗНАЧЕННЯ âij : ІНТУІТИВНЕ ОБЧИСЛЕННЯ ЧИСЕЛЬНИКА: ◦ НЕХАЙ ВІДОМЕ ДЕЯКЕ ЗНАЧЕННЯ ІМОВІРНОСТІ ДЛЯ ДАНОГО ПЕРЕХОДУ i j В МОМЕНТ ЧАСУ t ПОСЛІДОВНОСТІ СПОСТЕРЕЖЕННЯ. ◦ ЯКЩО ВІДОМА ЦЯ ІМОВІРНІСТЬ В КОЖЕН МОМЕНТ ЧАСУ t МОЖНА ПРОСУМУВАТИ І ОТРИМАТИ ЗАГАЛЬНУ КІЛЬКІСТЬ ПЕРЕХОДІВ i j. 2/10/2018 34
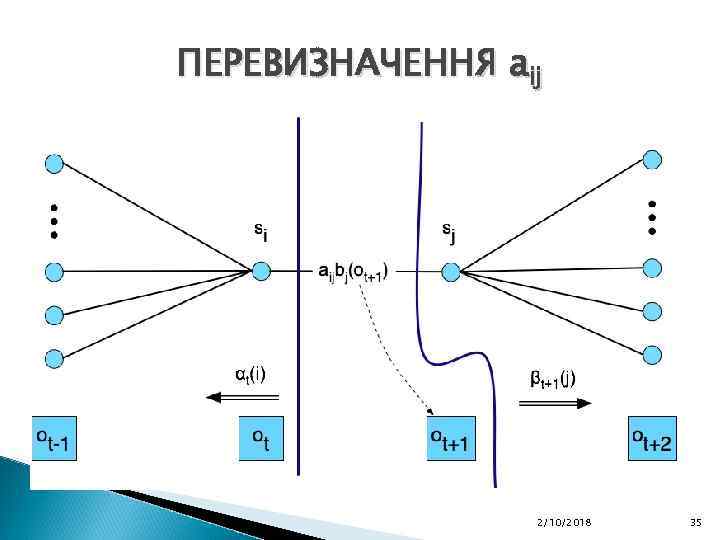
ПЕРЕВИЗНАЧЕННЯ aij 2/10/2018 35

ПЕРЕВИЗНАЧЕННЯ aij ВИЗНАЧИМО t ЯК ІМОВІРНІСТЬ ТОГО ЩО МИ В СТАНІ i В МОМЕНТ ЧАСУ t І У СТАНІ j В МОМЕНТ t+1, ПРИ ДАНИХ O 1. . T ТА λ: ОБЧИСЛИМО ЦЮ ІМОВІРНІСТЬ ЯК not-quite- : 2/10/2018 36

ОБЧИСЛЕННЯ not-quite- 2/10/2018 37

ОБЧИСЛЕННЯ НА ОСНОВІ not-quite- ПОТРІБНО: МАЄМО: ЗГІДНО ПОТРІБНО: 2/10/2018 38

ОБЧИСЛЕННЯ НА ОСНОВІ not-quite- 2/10/2018 39

ПЕРЕХІД ВІД to aij 2/10/2018 40

ПЕРЕВИЗНАЧЕННЯ bij ІМОВІРНІСТЬ ЩО ДАНИЙ СИМВОЛ v ГЕНЕРУЄТЬСЯ СТАНОМ j k НЕОБХІДНО ЗНАТИ ІМОВІРНІСТЬ ЗНАХОДЖЕННЯ В СТАНІ j В МОМЕНТ t Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 41

ПЕРЕВИЗНАЧЕННЯ bij Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 42
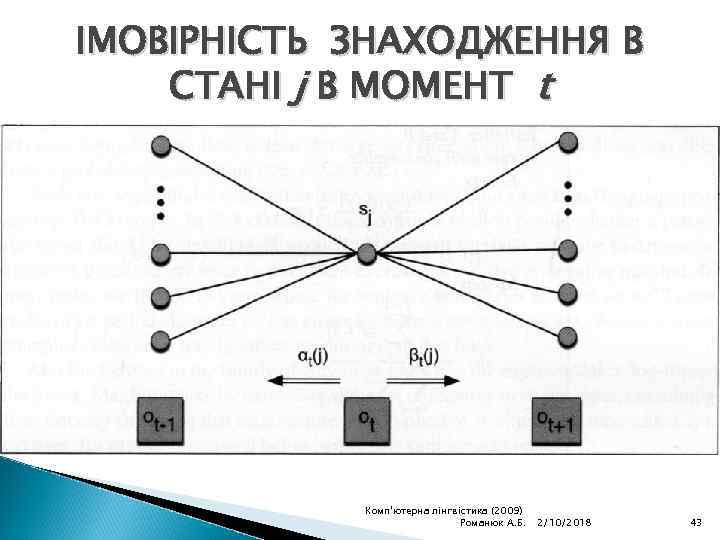
ІМОВІРНІСТЬ ЗНАХОДЖЕННЯ В СТАНІ j В МОМЕНТ t Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 43

АЛГОРИТМ “ВПЕРЕД-НАЗАД” Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 44

НЕОБХІДНО ПРОЧИТАТИ Daniel Jurafsky, James H. Martin Speech and Language Processing: an Introduction to Natural Language Processing, Computational Linguistics, and Speech Recognition - Second Edition Prentice Hall, 2008 -988. – Розділ, 6 ст. 173 -192. Комп'ютерна лінгвістика (2009) Романюк А. Б. 2/10/2018 45
KL-Lec8.ppt