Статистическое оценивание Основные описательные статистики Объем выборки

Статистическое оценивание

Основные описательные статистики Объем выборки N Среднее значение (среднее арифметическое) Дисперсия Стандартное отклонение Коэффициент вариации Размах R = xmax-xmin Медиана делит распределение на две равные части таким образом, что каждая часть содержит 50% всего распределения Мода равна тому значению, частота которого максимальна

Основные описательные статистики Геометрическое среднее применяют 1) когда переменная меняется во времени, а ее значения известны через равные промежутки времени 2) если отдельные значения в выборке далеко отстоят от остальных значений Взвешенные среднее и стандартное отклонение применяют, если нужно несколько (k) рядов данных объединить в один ряд Арифметическое среднее с весами применяют для измерений неравной точности В качестве весовых коэффициентов могут быть использованы обратные величины квадратов Пример: n 1=8 стандартных ошибок n 2=10 n 3=6 x 1=9 x 2=7 x 3=8 s 12=4 s 22=1 s 32=4

Выборка и генеральная совокупность Основные характеристики ВЫБОРОЧНОЙ совокупности: Среднее Стандартное отклонение Дисперсия: Основные характеристики ГЕНЕРАЛЬНОЙ совокупности: Генеральное среднее μ Стандартное отклонение генерального среднего σ Значения НЕИЗВЕСТНЫ выборочные параметры являются статистическими оценками генеральных параметров

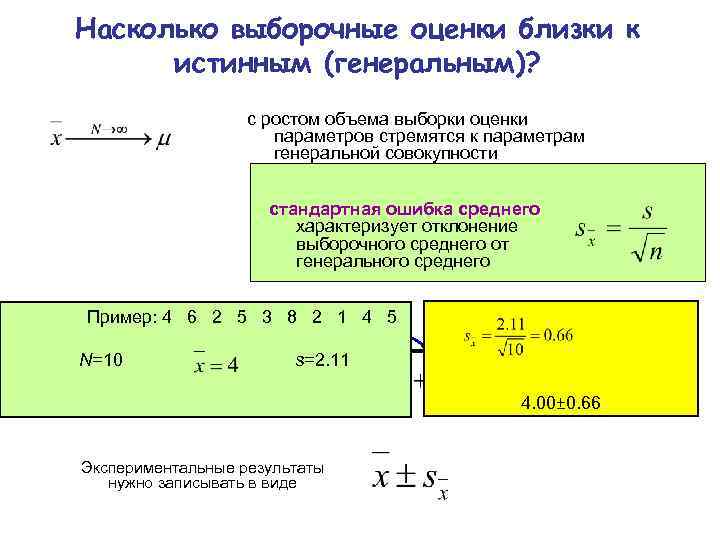
Насколько выборочные оценки близки к истинным (генеральным)? с ростом объема выборки оценки параметров стремятся к параметрам генеральной совокупности стандартная ошибка среднего характеризует отклонение выборочного среднего от генерального среднего Пример: 4 6 2 5 3 8 2 1 4 5 N=10 s=2. 11 4. 00± 0. 66 Экспериментальные результаты нужно записывать в виде

Стандартные ошибки сложных средних x, y, z – случайные величины, a, b, m - константы Случайная величина Стандартная ошибка среднего z = a+x z = ax Ответ: 1, 6 ± 0, 5 кг bx z=a e z=a lg (bx), Контрольные животные: прибавка в весе на 5, 3 ± 0, 3 кг УФ-облученные животные: прибавка в весе на 6, 8 ± 0, 4 кг Какое увеличение веса дает УФ-облучение? z=xm z=x±y

Стандартные ошибки сложных средних z=xy или z=x/y Закон преобразования ошибок степенных произведений. Пусть h = kxaybzc… где x, y, z – переменные, k, a, b, c – константы средняя относительная ошибка С 1 кв. м собрали 247 ± 8 колосьев пшеницы. Вес колоса – 851 ± 14 мг. Какова урожайность сорта (в ц/га)?

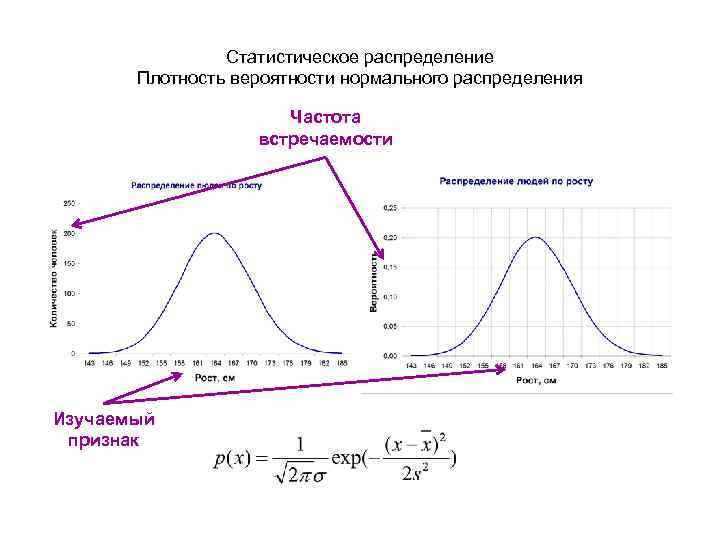
Статистическое распределение Плотность вероятности нормального распределения Частота встречаемости Изучаемый признак

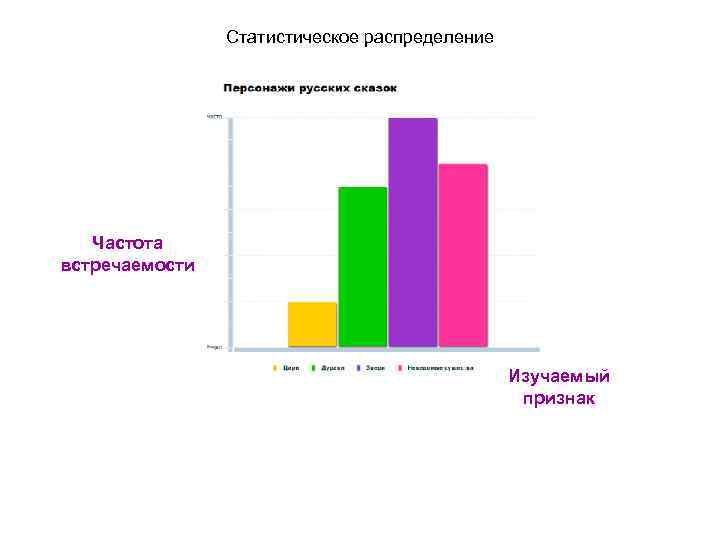
Статистическое распределение Частота встречаемости Изучаемый признак

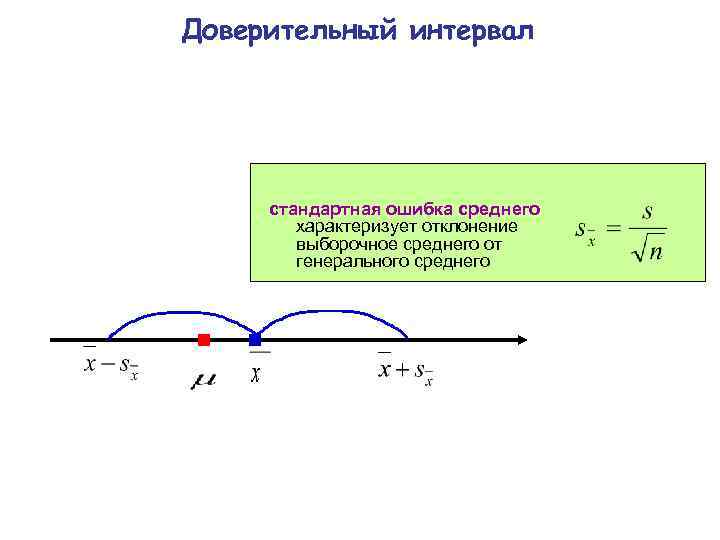
Доверительный интервал стандартная ошибка среднего характеризует отклонение выборочное среднего от генерального среднего

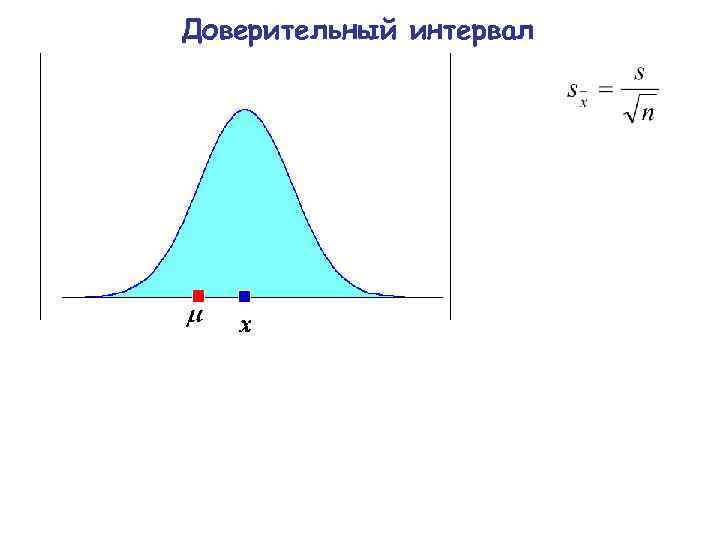
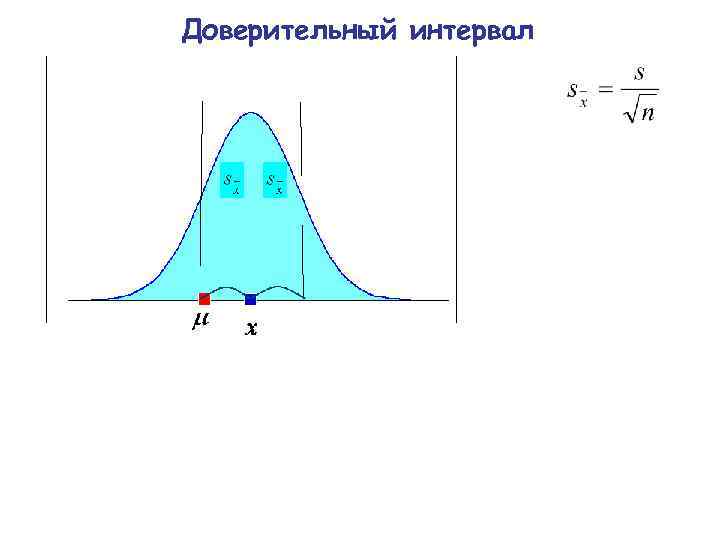
Доверительный интервал

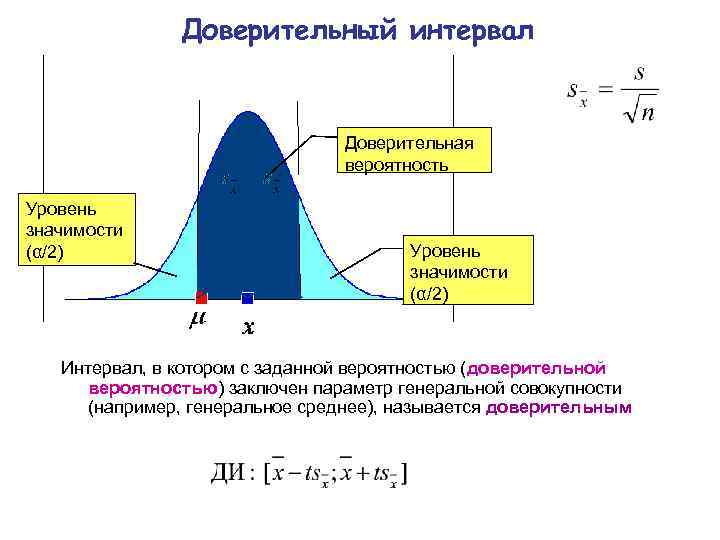
Доверительный интервал Доверительная вероятность Уровень значимости (α/2) Интервал, в котором с заданной вероятностью (доверительной вероятностью) заключен параметр генеральной совокупности (например, генеральное среднее), называется доверительным

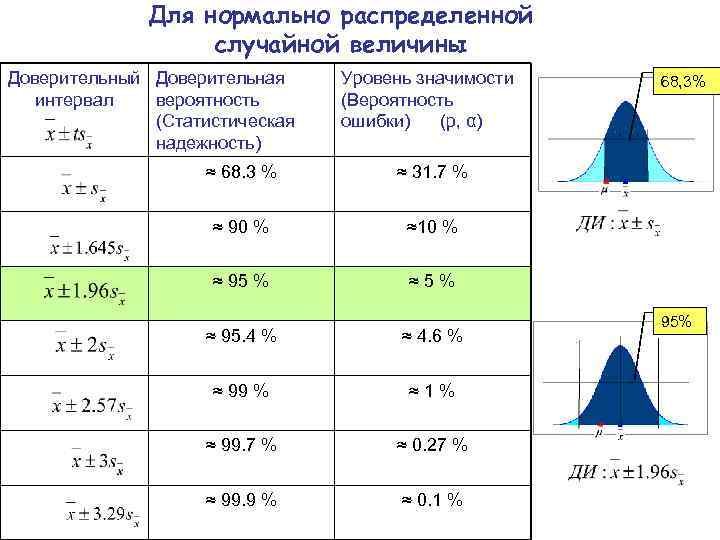
Для нормально распределенной случайной величины Доверительный Доверительная интервал вероятность (Статистическая надежность) Уровень значимости (Вероятность ошибки) (p, α) ≈ 68. 3 % ≈ 31. 7 % ≈ 90 % ≈10 % ≈ 95 % 68, 3% ≈ 5 % ≈ 95. 4 % ≈ 4. 6 % ≈ 99 % ≈ 1 % ≈ 99. 7 % ≈ 0. 27 % ≈ 99. 9 % ≈ 0. 1 % 95%

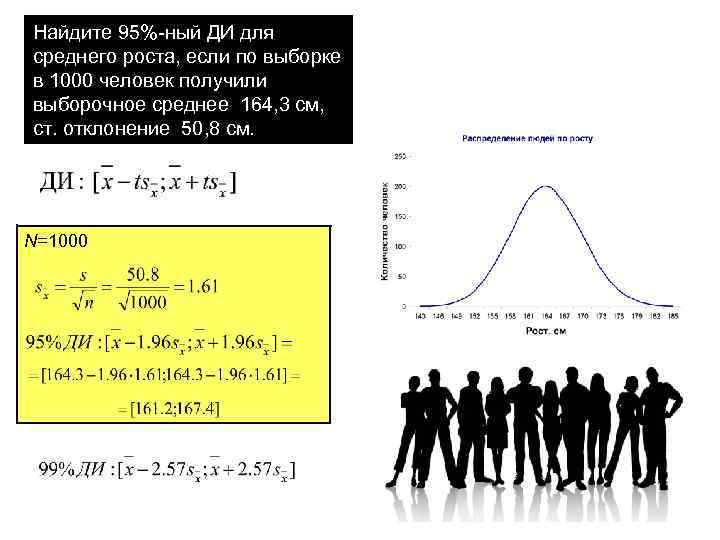
Найдите 95%-ный ДИ для среднего роста, если по выборке в 1000 человек получили выборочное среднее 164, 3 см, ст. отклонение 50, 8 см. N=1000

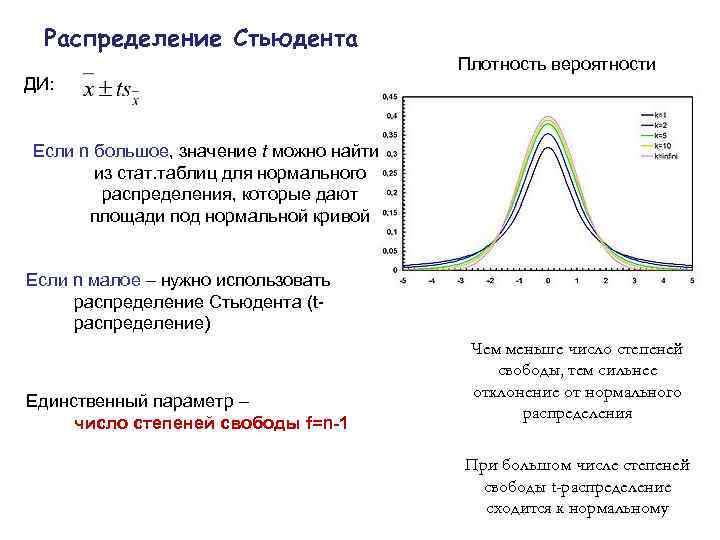
Распределение Стьюдента Плотность вероятности ДИ: Если n большое, значение t можно найти из стат. таблиц для нормального распределения, которые дают площади под нормальной кривой Если n малое – нужно использовать распределение Стьюдента (tраспределение) Единственный параметр – число степеней свободы f=n-1 Чем меньше число степеней свободы, тем сильнее отклонение от нормального распределения При большом числе степеней свободы t-распределение сходится к нормальному

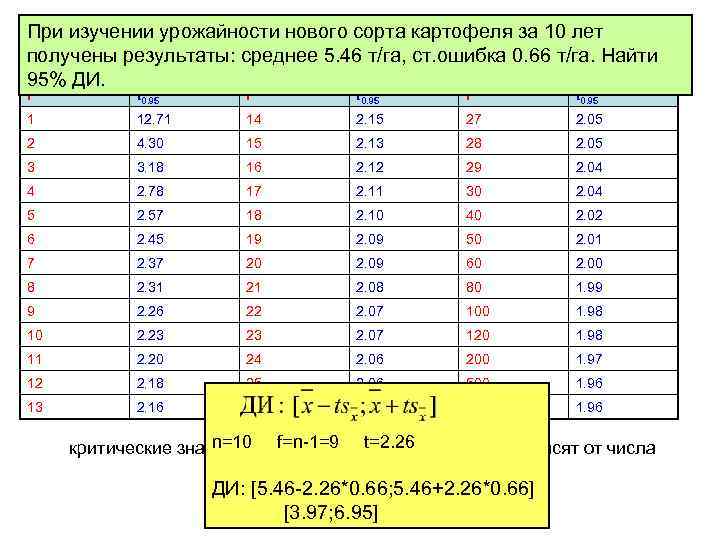
При изучении урожайности нового сорта картофеля за 10 лет Критические значения t-распределения для 95 -% доверительной получены результаты: среднее 5. 46 т/га, ст. ошибка 0. 66 т/га. Найти вероятности 95% ДИ. f t 0. 95 1 12. 71 14 2. 15 27 2. 05 2 4. 30 15 2. 13 28 2. 05 3 3. 18 16 2. 12 29 2. 04 4 2. 78 17 2. 11 30 2. 04 5 2. 57 18 2. 10 40 2. 02 6 2. 45 19 2. 09 50 2. 01 7 2. 37 20 2. 09 60 2. 00 8 2. 31 21 2. 08 80 1. 99 9 2. 26 22 2. 07 100 1. 98 10 2. 23 23 2. 07 120 1. 98 11 2. 20 24 2. 06 200 1. 97 12 2. 18 25 2. 06 500 1. 96 13 2. 16 26 2. 06 >> 1. 96 n=10 f=n-1=9 t=2. 26 критические значения t-статистики особенно сильно зависят от числа степеней свободы ДИ: [5. 46 -2. 26*0. 66; 5. 46+2. 26*0. 66] при малом объеме выборки [3. 97; 6. 95]

Оптимальный объем выборки - минимальный объем выборки, необходимый для получения среднего значения с определенной точностью δ При измерении массы 100 лабораторных животных получили среднее 130, 3 мг, ст. отклонение 4. 3 мг. Каков должен быть объем выборки, чтобы с вероятностью 95% неточность в определении среднего была не больше, чем 0. 1 мг? n=100 δ=0. 1 мг t=1. 98 nmin=(1. 98*4. 3/0. 1)2=7250

Оптимальный объем выборки 4 6 2 5 3 8 2 1 4 5 Достаточен ли объем выборки для того, чтобы среднее значение - минимальный объем выборки, выборки было определено с относительной вероятной ошибкой необходимый для получения среднего 25% на уровне 95% доверительной вероятности? значения с определенной точностью δ - минимальный объем выборки, необходимый для получения среднего значения с относительной вероятной ошибкой ε