СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ СОЦИАЛЬНОЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ Основные приемы

СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ СОЦИАЛЬНОЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ

Основные приемы и методы изучения взаимосвязей: • 1. Метод сопоставления параллельных рядов: показатели, характеризующие факторный признак, ранжируются, а затем параллельно им располагаются соответствующие показатели результативного признака. Сравнение построенных рядов дает возможность не только подтвердить само наличие связи, но и выявить ее направление.

Метод сопоставления параллельных рядов Х 1 2 3 4 5 6 У 1 3 6 4 10 17 20 У 2 20 17 10 4 6 3 х – разряд рабочего; y 1 – выработка, y 2 – количество времени, затрачиваемого на производство 1 -й детали. Т. о. с увеличением факторного признака х, значения результатного признака y 1 возрастают. Следовательно, имеет место прямая связь между двумя этими показателями

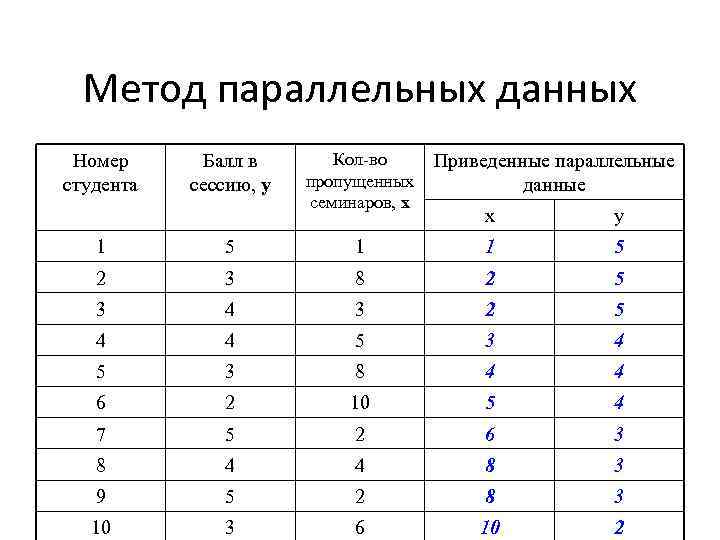Метод параллельных данных Номер студента Балл в сессию, y Кол-во Приведенные параллельные пропущенных данные семинаров, x x y 1 5 1 1 5 2 3 8 2 5 3 4 3 2 5 4 4 5 3 8 4 4 6 2 10 5 4 7 5 2 6 3 8 4 4 8 3 9 5 2 8 3 10 3 6 10 2

При значительном количестве единиц сравниваемых рядов целесообразнее воспользоваться корреляционными таблицами или решетками • в подлежащем располагаются значения факторного признака, в сказуемом – результативного. В клетках, образовавшихся при пересечении строк и граф, указываются частоты, т. е. число случаев, в которых одни значения сочетаются с другими

Корреляционная таблица X Y y 1 y 2 ym Итого x 1 φ12 φ1 n ∑φij x 2 φ21 φ22 φ2 n ∑φij xn φn 1 φn 2 φnm ∑φij Итого ∑φji

Если значения х и у расположены в возрастающем порядке, то сосредоточение частот около диагонали таблицы, идущей с левого верхнего угла в правый нижний, свидетельствует о прямой связи между изучаемыми признаками, а с правого верхнего угла в левый нижний – об обратной связи, причем связь будет тем теснее, чем плотнее концентрируются частоты у диагонали. Если частоты расположены по всей таблице равномерно, то это говорит о слабой связи между признаками или об отсутствии ее

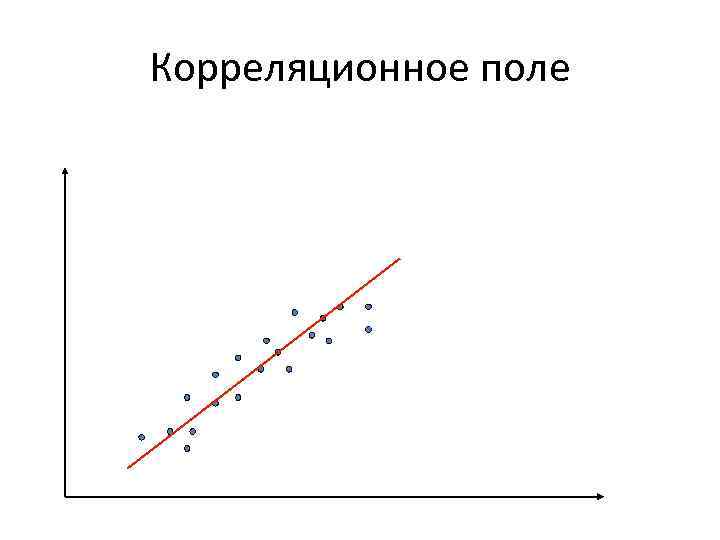Корреляционное поле

Метод аналитических группировок • 1. все единицы совокупности разбивают на определенные группы по возрастанию факторного признака • 2. по каждой группе рассчитывается средняя величина результатного признака. 3. Если с возрастанием факторного признака, при переходе от группы к группе, происходит возрастание или убывание результатного признака, значит можно сделать вывод о наличии связи и ее направлении.

Корреляционный анализ (КРА)– • метод математической статистики, изучающий корреляционные (статистические) связи

Типы связей между различными явлениями и их признаками: По характеру зависимости между факторными и результатными признаками: 1. функциональные или строго детерминированные (от латинского determinatio – ограничение, определение), при которых каждому значению факторного признака (аргумента) соответствует одно или несколько строго определенных значений результативного признака (функции), т. е изменение значения результатного признака полностью зависит от изменения значения факторного признака

По характеру зависимости между факторными и результатными признаками: 2. стохастические, т. е. вероятностные, нестрогие; не имеют ограничений и условий, присущих функциональным связям; т. е. разным значениям одной переменной соответствуют разные распределения значений другой переменной. 3. Частным случаем стохастических связей являются корреляционные (статистические) связи, при которых каждому значению факторного признака x соответствует среднее значение результатного признака y; проявляется в виде тенденции изменений средних значений результатного признака в зависимости от изменений факторного признака.

Корреляционные связи являются нестрогими, неполными, вероятностными и проявляются только в средних величинах при наличии следующих условий: 1. Если имеются данные по достаточно большой совокупности явлений. 2. Если закономерность, проявляющаяся в данном явлении, надежно выражена в средней величине. 3. Если распределение совокупности по результативному и факторным признакам подчиняется нормальному закону распределения вероятностей (связано с МНК)

Классификации корреляционных связей: • По аналитическому выражению формы зависимости: прямолинейные (линейные) и нелинейные (криволинейные). ; • По числу взаимодействующих факторов: парная и множественная; • По степени тесноты: если значению факторного признака x соответствуют близкие другу (тесно расположенные около своей средней) значения результатного признака y – связь является тесной; если значения результатного признака, при одном и том же значении факторного варьируют (изменяются) значительно – связь менее тесная.

Методы оценки тесноты связи: • Методами корреляционного и дисперсионного анализа (все изучаемые признаки являются количественными) вычисляются основные параметры распределения (средние величины, дисперсии), поэтому они получили название параметрических. • измерение связи между качественными признаками (пол, образование, занятие, семейное состояние, форма собственности предприятия. . ) производится с помощью непараметрических методов (не используя параметры распределения)

Показатели тесноты связи между признаками называют коэффициентами корреляции Их выбор зависит от того, в каких шкалах измеряются признаки: • количественная шкала: корреляционное отношение, ЛКК; • порядковая шкала – упорядоченность объектов по признакам, рангам: коэф-т Спирмена, коэф-т Кенделла; • номинальная шкала – перечень характеристик объекта, шкала наименований: коэф-т ассоциации и контингенции, коэф-ты Пирсона и Чупрова

количественная шкала: степень тесноты связи изучается методами корреляционного и дисперсионного анализа • Дисперсионный анализ (см. лекцию «Показатели вариации» : общая дисперсия, межгрупповая, внутригрупповая; правило сложения дисперсий; эмпирический коэффициент детерминации и эмпирическое корреляционное отношение)

Эмпирический коэффициент детерминации • характеризует долю межгрупповой дисперсии в общей дисперсии и показывает насколько вариация признака в совокупности обусловлена фактором группировки

Эмпирическое корреляционное отношение (индекс корреляции) оценивает тесноту связи между изучаемым и группировочными признаками (колеблется в пределах от 0 до 1, чем ближе к единице, тем теснее связь)

В случае линейной зависимости тесноту связи можно измерить при помощи линейного коэффициента корреляции (ЛКК), (от -1 (полная обратная зависимость) до +1(полная прямая зависимость)

Линейный коэффициент корреляции Величина коэффициента корреляции Характер связи До | ± 0, 3 | Практически отсутствует | ± 0, 3 | - | ± 0, 5 | Слабая | ± 0, 5 | - | ± 0, 7 | Умеренная | ± 0, 7 | - | ± 1, 0 | Сильная

Значимость ЛКК проверяется на достоверность (надежность). • корреляционная связь является достоверной лишь при достаточном числе наблюдений (не менее 20– 30). Проверка надежности коэффициента корреляции осуществляется с помощью критерия надежности Стьюдента по формуле: • tr = r / r • где r – среднеквадратическая ошибка коэффициента корреляции r = (1 -r 2) / √n-1, n- число наблюдений Если tr ≥ 3, то r считается надежным, а связь доказанной с вероятностью 0, 997. Если tr < 3, связь нельзя считать достоверной.

Номинальная шкала (используются непараметрические методы): • При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативного признака, используют коэффициент ассоциации или коэффициент контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным

Номинальные шкалы X Y 1 2 1 a b a+b 2 c d c+d a+c b+d

Коэффициент ассоциации Если ka > 0, 5, то между признаками имеется существенная взаимосвязь В тех случаях, когда хотя бы один из четырех показателей в «таблице четырех полей» отсутствует, величина коэффициента ассоциации будет равна единице, что дает преувеличенную оценку степени тесноты связи между признаками, и предпочтение следует отдать коэффициенту контингенции (КK):

Коэффициент контингенции Если kk ≥ 0, 3, то между признаками имеется существенная взаимосвязь

Если каждый из качественных признаков состоит из большого числа групп (более двух), то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова. Для данных коэффициентов необходимо составить таблицу взаимной сопряженности.

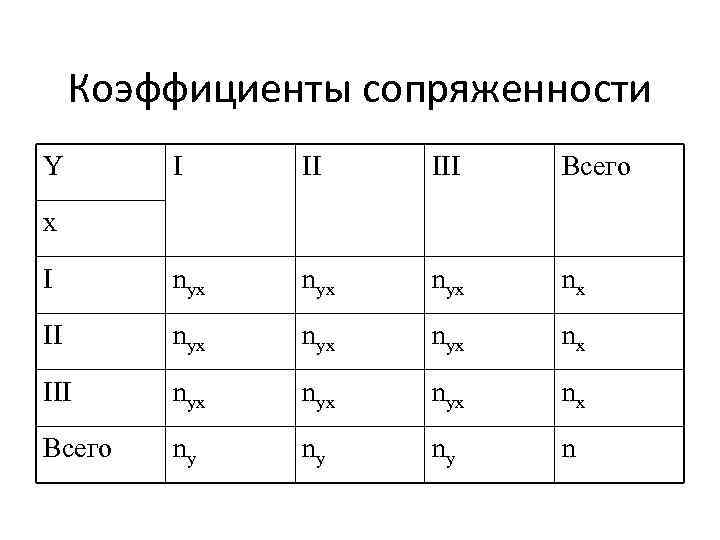Коэффициенты сопряженности Y I II III Всего I nyx nyx nyx nx III nyx nyx nx Всего ny ny ny n x

Коэффициент сопряженности Пирсона где Φ 2 -показатель взаимной сопряженности ; nxy- частота каждой клетки таблицы взаимной сопряженности; nx, ny -итоговые частоты соответствующих строк и столбцов;

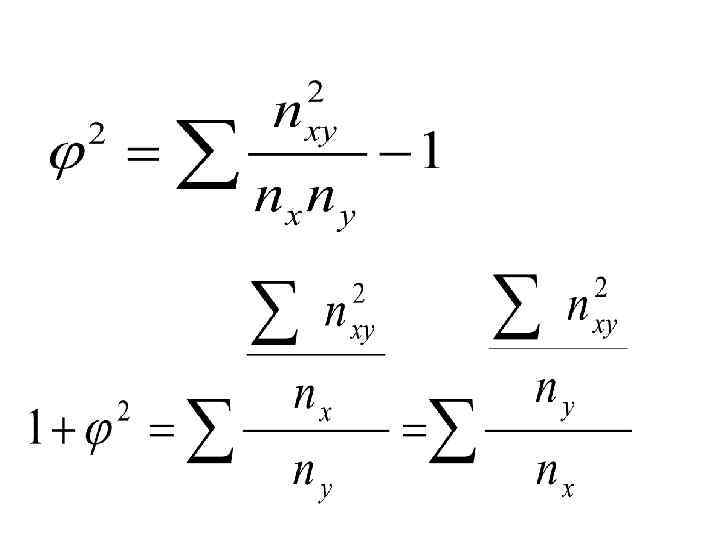
Коэффициент сопряженности Чупрова m 1 – количество градаций первого признака (число строк) m 2 – количество градаций второго признака (число столбцов)

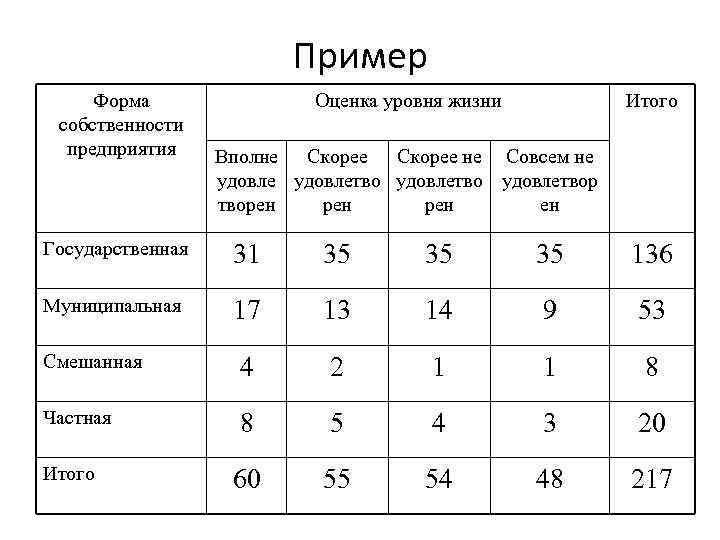Пример Форма собственности предприятия Оценка уровня жизни Итого Вполне Скорее не Совсем не удовлетвор творен рен ен Государственная 31 35 35 35 136 Муниципальная 17 13 14 9 53 Смешанная 4 2 1 1 8 Частная 8 5 4 3 20 60 55 54 48 217 Итого

Пример

Пример свидетельствуют о наличие слабой связи между формой собственности предприятия и уровнем жизни работников. Чем ближе величины КП и КЧ к 1, тем теснее связь.

В случае, если признак не выражается количественно, однако единицы совокупности можно упорядочить применяется ранжирование (порядковая шкала) • Т. е. каждой единице совокупности присваивается ранг, - порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Измерение связи между ранжированными признаками производится с помощью ранговых коэффициентов корреляции Спирмена и Кендэлла

Ранговый коэффициент корреляции Спирмена

Ранговый коэффициент корреляции Кенделла S – сумма баллов, если баллом +1 оценивается пара рангов, имеющих по обоим показателям одинаковый порядок, а баллом -1 – пара с разным порядком.

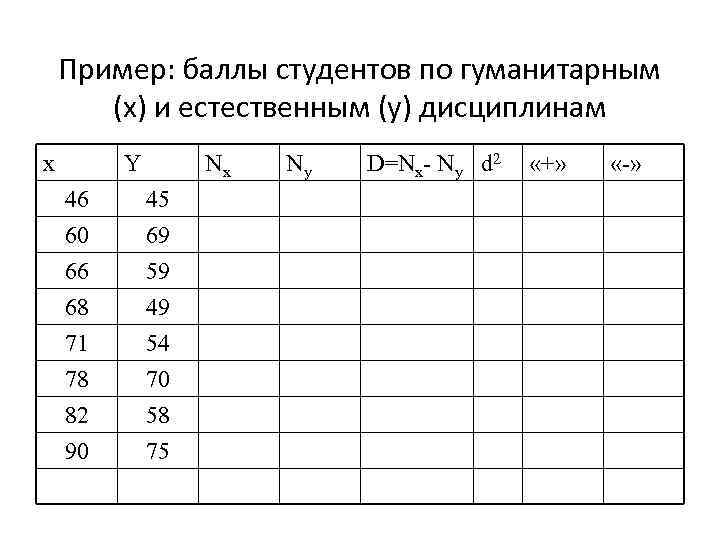Пример: баллы студентов по гуманитарным (x) и естественным (y) дисциплинам x Y Nx 46 60 66 45 69 59 68 71 78 82 90 49 54 70 58 75 Ny D=Nx- Ny d 2 «+» «-»

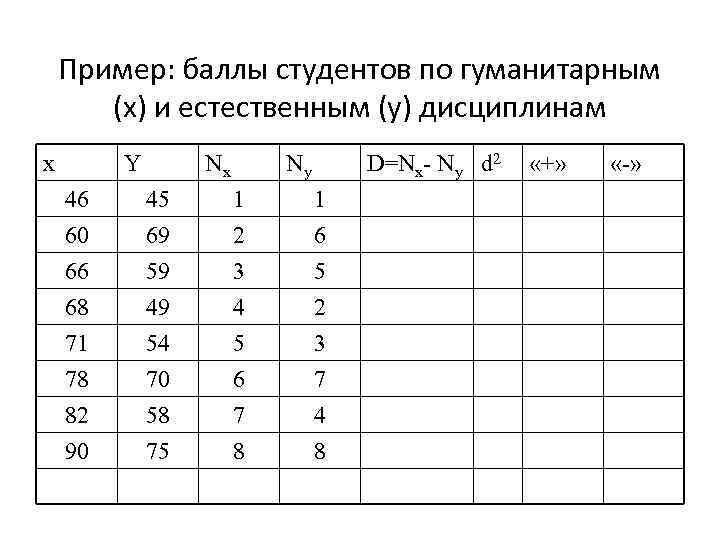Пример: баллы студентов по гуманитарным (x) и естественным (y) дисциплинам x Y Nx Ny D=Nx- Ny d 2 46 60 66 45 69 59 1 2 3 1 6 5 68 71 78 82 90 49 54 70 58 75 4 5 6 7 8 2 3 7 4 8 «+» «-»

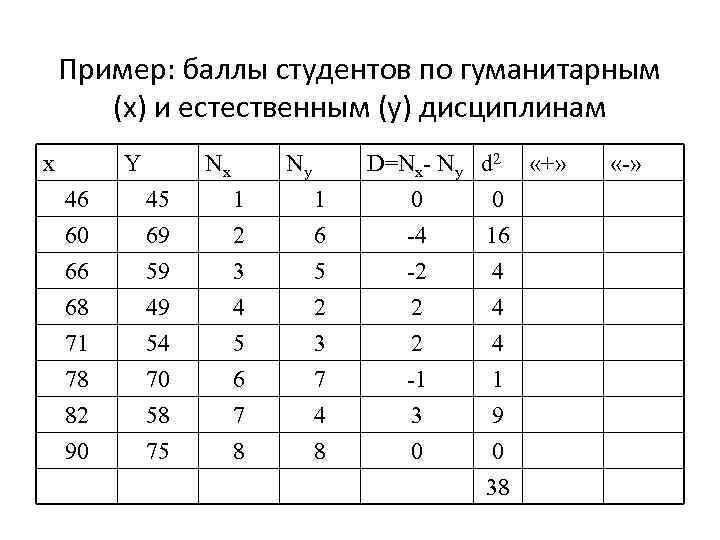Пример: баллы студентов по гуманитарным (x) и естественным (y) дисциплинам x Y Nx Ny 46 60 66 45 69 59 1 2 3 1 6 5 68 71 78 82 90 49 54 70 58 75 4 5 6 7 8 2 3 7 4 8 D=Nx- Ny d 2 «+» 0 0 -4 16 -2 4 2 2 -1 3 0 4 4 1 9 0 38 «-»

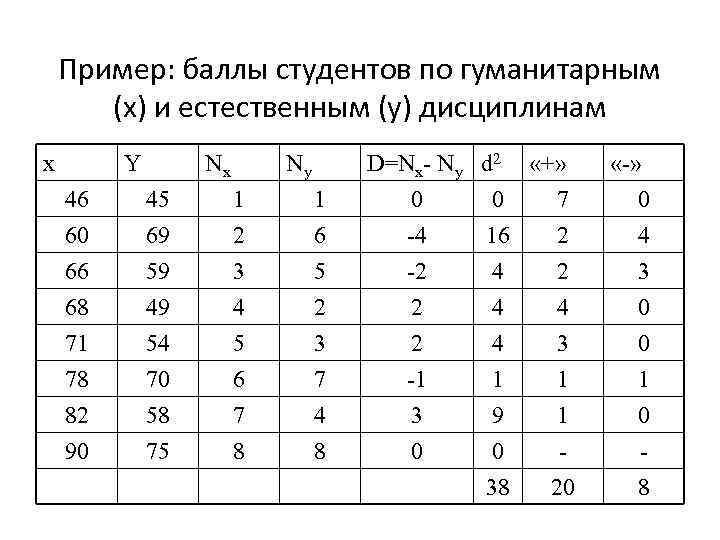Пример: баллы студентов по гуманитарным (x) и естественным (y) дисциплинам x Y Nx Ny 46 60 66 45 69 59 1 2 3 1 6 5 68 71 78 82 90 49 54 70 58 75 4 5 6 7 8 2 3 7 4 8 D=Nx- Ny d 2 «+» 0 0 7 -4 16 2 -2 4 2 2 2 -1 3 0 4 4 1 9 0 38 4 3 1 1 20 «-» 0 4 3 0 0 1 0 8

Ранговый коэффициент корреляции Спирмена

Ранговый коэффициент корреляции Кенделла

Этапы КРА 1) установление наличия связи между изучаемыми признаками при помощи указанных выше методов; 2) отбор наиболее существенных факторов для анализа; 3) определение характера связи, ее направления и формы, т. е. подбор математического уравнения, выражающего зависимость между y и x; 4) определение параметров уравнения и показателей тесноты связи; 5) статистическая оценка показателей тесноты связи

Парная линейная корреляция -простейшая система корреляционной связи между двумя признаками Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид: Уср = а + b х , где Уср - среднее значение результативного признака при определенном значении факторного признака х; a – свободный член уравнения; b – коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения – (вариация у, приходящаяся на единицу вариации х) • b всегда – число именованное. Если: b > 0, то связь прямая; • b < 0, – связь обратная; • b = 0 , – связь отсутствует

Построение уравнения регрессии Параметры уравнения регрессии определяют из системы нормальных уравнений, отвечающей требованию метода наименьших квадратов (МНК).

Построение уравнения регрессии Для линейной зависимости: Сущность заключается в том, что величина параметров функции должна быть такой, чтобы достигался минимум суммы квадратов отклонений между теоретическими (ух) и фактическими (у) значениями зависимого показателя. Если моделью исследуемой зависимости выбрано уравнение прямой, то а 0 и а 1 необходимо рассчитать так, чтобы

Построение уравнения регрессии Поскольку х и у заданы, то S является величиной, зависимой от определяемых параметров а 0 и ах: Так как производная функции в точке минимума равна нулю, на основе можно записать:

Построение уравнения регрессии После преобразований эта система уравнений принимает вид:

Построение уравнения регрессии Системы нормальных уравнений решаются различными способами, чаще всего с помощью определителей. В результате получают следующие выражения:

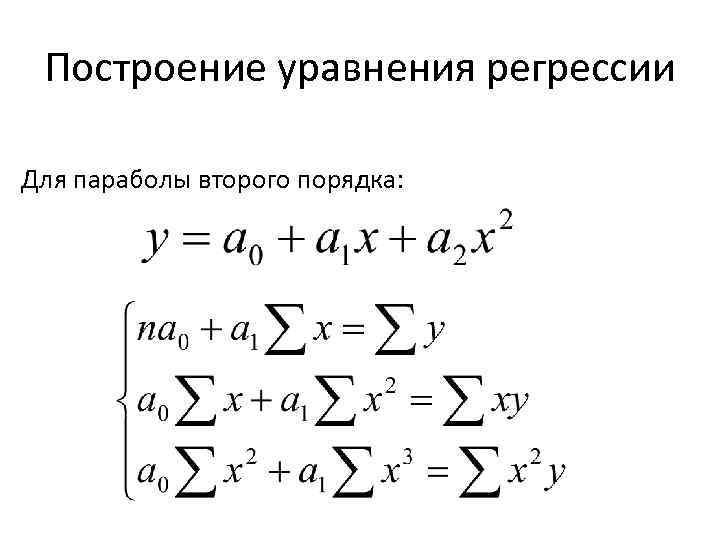Построение уравнения регрессии Для параболы второго порядка:

Построение уравнения регрессии Для гиперболы:

Оценка построенных функций. После получения функций производится их оценка. Если в качестве исходной информации использовалась вся генеральная совокупность, а не данные выборки, то оценку осуществляют по так называемым показателям тесноты связи. Если построена линейная однофакторная зависимость, то для ее оценки вычисляют коэффициент парной линейной корреляции:

К числу важнейших аналитических характеристик относятся: üкоэффициент детерминации, üсредняя и предельная эффективность ресурса, üкоэффициент эластичности, üнорма взаимозаменяемости факторов

Коэффициент детерминации характеризует Слабая удельный вес <10% факторного признака или признаков в 10% - 50% Средняя общей вариации зависимого >50% Сильная показателя. 100% Полная

Средняя эффективность ресурса определяется путем деления соответствующей функции на объем использованного ресурса. Эффективность измеряется в единицах результативного показателя в расчете на единицу ресурса.

Предельная эффективность ресурса измеряется в единицах зависимого показателя в расчете на единицу факторного признака.

Эластичность - показывает, на сколько процентов изменяется результативный показатель у с отклонением факторного признака х на 1%, т. е. представляет собой соотношение темпов прироста у и х. При линейной производственной функции у = ао+а 1 х эластичность составляет:

Оценка значимости параметров взаимосвязи Стандартная ошибка коэффициента корреляции:

Оценка значимости параметров взаимосвязи Значимость rxy Если tрасч больше теоретического (табличного) значения критерия Стьюдента (tтабл) для заданного уровня вероятности и (n - 2) степеней свободы, то можно утверждать, что rxy значимо.

Оценка значимости параметров взаимосвязи Вывод о правильности выбора вида взаимосвязи и характеристику значимости всего уравнения регрессии получают с помощью F-критерия, вычисляя его расчетное значение.

Оценка значимости параметров взаимосвязи где n - число наблюдений; m - число параметров уравнения регрессии. Fрасч также должно быть больше Fтеор при v 1 = (m - 1) и v 2 = (n - m) степенях свободы.

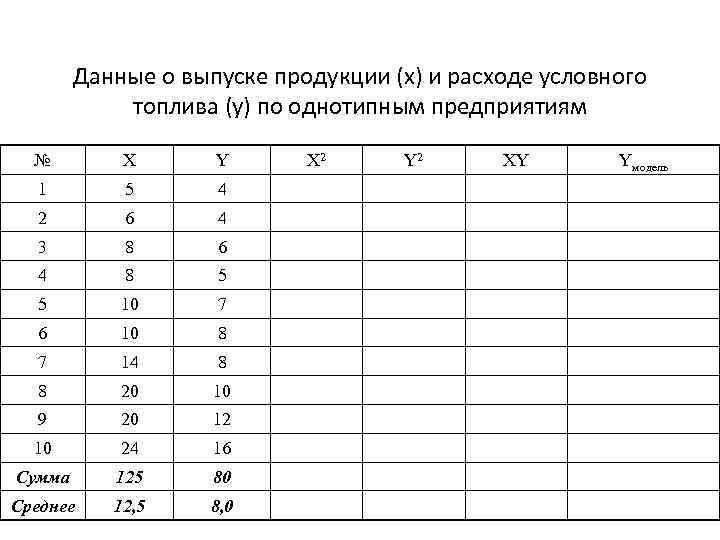Данные о выпуске продукции (х) и расходе условного топлива (у) по однотипным предприятиям № X Y 1 5 4 2 6 4 3 8 6 4 8 5 5 10 7 6 10 8 7 14 8 8 20 10 9 20 12 10 24 16 Сумма 125 80 Среднее 12, 5 8, 0 X 2 Y 2 XY Yмодель

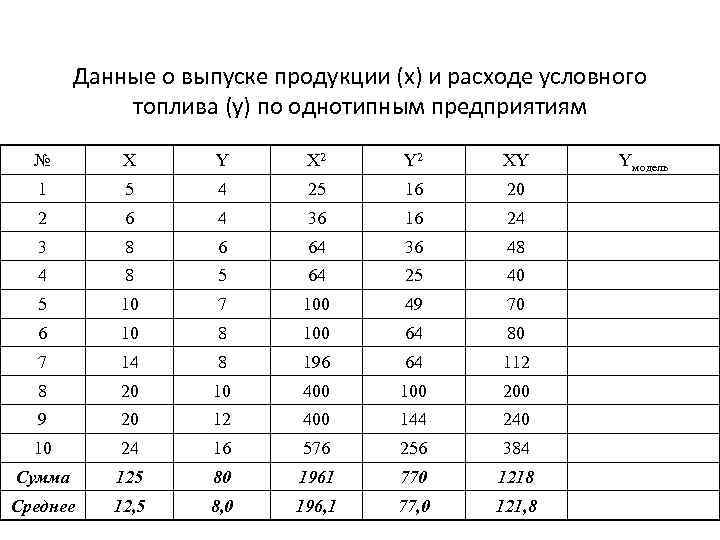Данные о выпуске продукции (х) и расходе условного топлива (у) по однотипным предприятиям № X Y X 2 Y 2 XY 1 5 4 25 16 20 2 6 4 36 16 24 3 8 6 64 36 48 4 8 5 64 25 40 5 10 7 100 49 70 6 10 8 100 64 80 7 14 8 196 64 112 8 20 10 400 100 200 9 20 12 400 144 240 10 24 16 576 256 384 Сумма 125 80 1961 770 1218 Среднее 12, 5 8, 0 196, 1 77, 0 121, 8 Yмодель

Коэффициент корреляции

Определение параметров уравнения регрессии

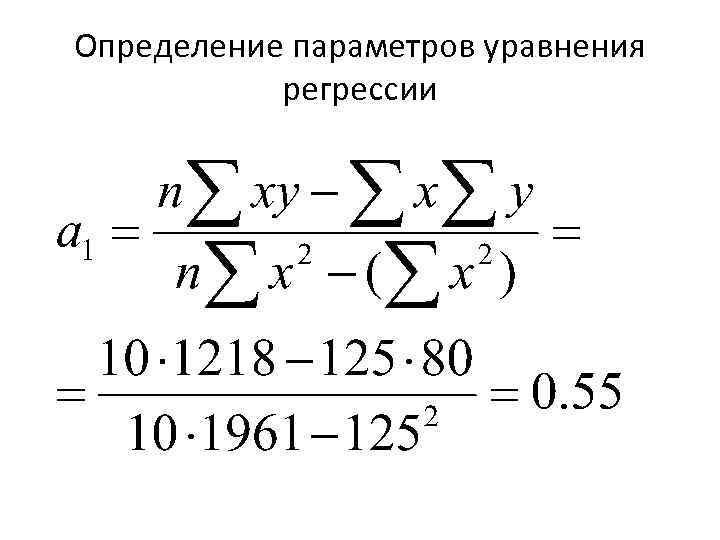Определение параметров уравнения регрессии

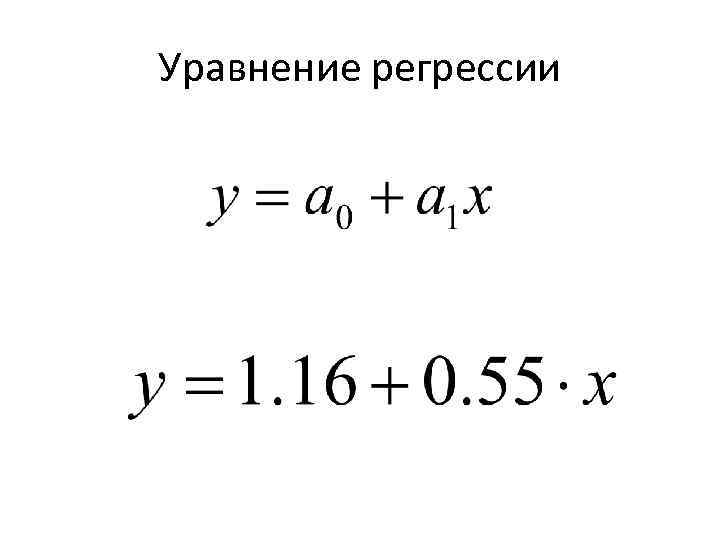Уравнение регрессии

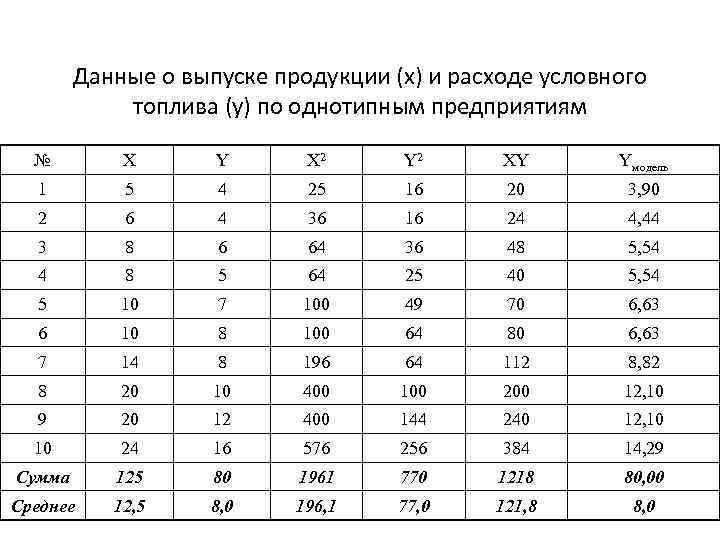Данные о выпуске продукции (х) и расходе условного топлива (у) по однотипным предприятиям № X Y X 2 Y 2 XY Yмодель 1 5 4 25 16 20 3, 90 2 6 4 36 16 24 4, 44 3 8 6 64 36 48 5, 54 4 8 5 64 25 40 5, 54 5 10 7 100 49 70 6, 63 6 10 8 100 64 80 6, 63 7 14 8 196 64 112 8, 82 8 20 10 400 100 200 12, 10 9 20 12 400 144 240 12, 10 10 24 16 576 256 384 14, 29 Сумма 125 80 1961 770 1218 80, 00 Среднее 12, 5 8, 0 196, 1 77, 0 121, 8 8, 0

Аналитические характеристики производственных функций и их экономическая трактовка.

Аналитические характеристики производственных функций и их экономическая трактовка.