СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ ВЗАИМОСВЯЗИ факторные признаки По

СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ

ВЗАИМОСВЯЗИ факторные признаки По характеру проявления результативные признаки Ø Функциональные Ø Статистические Ø Корреляционные • Однофакторные (парные) • Многофакторные (множественные) По направлению действия Ø Прямая Ø Обратная Ø Линейные По форме (прямолинейные) Ø Нелинейные (криволинейные)

КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

Э Т А П Ы К О Р Р Е Л Я Ц И О Н Н О Г О А Н А Л И З А I Построение поля корреляции y y x II x Расчет и интерпретация коэффициента корреляции III Оценка статистической значимости коэффициента корреляции Ø Альтернативные гипотезы (H 0, H 1) Ø Наблюдаемое значение t-критерия Стьюдента (tнабл) Ø Сравнение tнабл и tтабл (tнабл < tтабл H 0 tнабл > tтабл H 1 )

КОЭФФИЦИЕНТ Абсолютная величина коэффициента корреляции До 0, 3 - 0, 5 – 0, 7 и выше КОРРЕЛЯЦИИ Интерпретация Связь практически отсутствует Слабая связь Умеренная связь Сильная связь

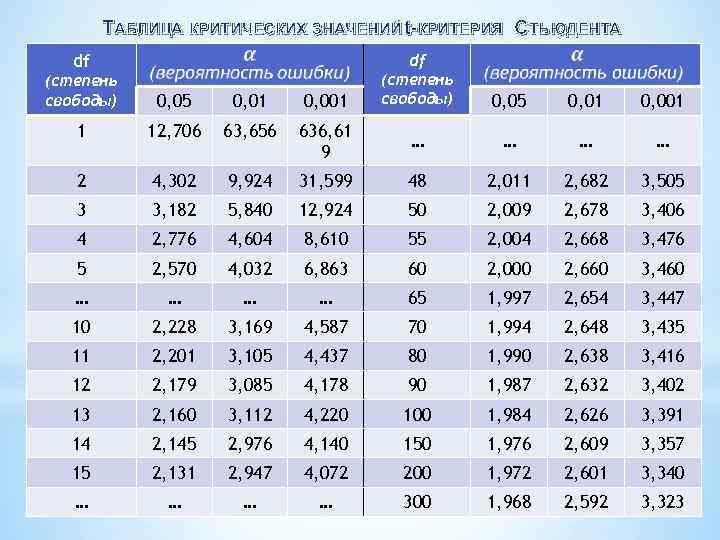ТАБЛИЦА КРИТИЧЕСКИХ ЗНАЧЕНИЙ t-КРИТЕРИЯ СТЬЮДЕНТА df df (степень свободы) 0, 05 0, 01 0, 001 1 12, 706 63, 656 636, 61 9 … … 2 4, 302 9, 924 31, 599 48 2, 011 2, 682 3, 505 3 3, 182 5, 840 12, 924 50 2, 009 2, 678 3, 406 4 2, 776 4, 604 8, 610 55 2, 004 2, 668 3, 476 5 2, 570 4, 032 6, 863 60 2, 000 2, 660 3, 460 … … 65 1, 997 2, 654 3, 447 10 2, 228 3, 169 4, 587 70 1, 994 2, 648 3, 435 11 2, 201 3, 105 4, 437 80 1, 990 2, 638 3, 416 12 2, 179 3, 085 4, 178 90 1, 987 2, 632 3, 402 13 2, 160 3, 112 4, 220 100 1, 984 2, 626 3, 391 14 2, 145 2, 976 4, 140 150 1, 976 2, 609 3, 357 15 2, 131 2, 947 4, 072 200 1, 972 2, 601 3, 340 … … 300 1, 968 2, 592 3, 323

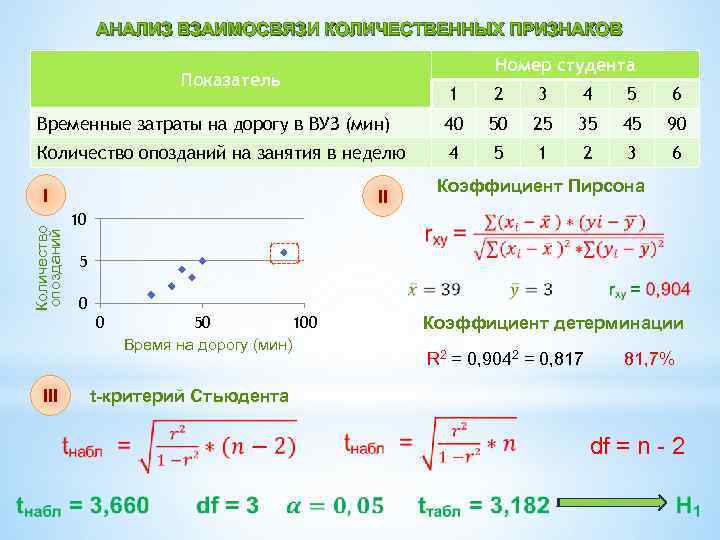АНАЛИЗ ВЗАИМОСВЯЗИ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ Номер студента Показатель 1 2 3 4 5 6 Временные затраты на дорогу в ВУЗ (мин) 40 50 25 35 45 90 Количество опозданий на занятия в неделю 4 5 1 2 3 6 I Количество опозданий 10 5 0 0 III Коэффициент детерминации 50 100 Время на дорогу (мин) R 2 = 0, 9042 = 0, 817 81, 7% t-критерий Стьюдента Коэффициент Пирсона II df = n - 2

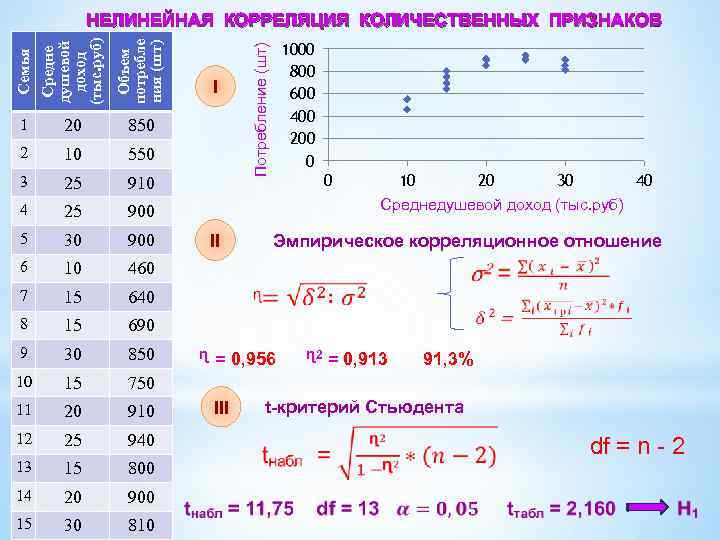1 20 10 550 3 25 910 4 25 900 5 30 900 6 10 460 7 15 640 8 15 690 9 30 850 10 15 750 11 20 910 12 25 940 13 15 800 14 20 900 15 30 810 I 850 2 1000 800 600 400 200 0 Потребление (шт) Объем потребле ния (шт) Семья Средне душевой доход (тыс. руб) НЕЛИНЕЙНАЯ КОРРЕЛЯЦИЯ КОЛИЧЕСТВЕННЫХ ПРИЗНАКОВ 0 10 20 30 40 Среднедушевой доход (тыс. руб) Эмпирическое корреляционное отношение II ᶯ = 0, 956 III ᶯ 2 = 0, 913 91, 3% t-критерий Стьюдента df = n - 2

ЭМПИРИЧЕСКОЕ КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕ Характер связи ᶯ 0, 1 – 0, 3 очень слабая 0, 3 – 0, 5 умеренная 0, 5 – 0, 7 заметная 0, 7 – 0, 9 тесная 0, 9 – 0, 99 весьма тесная ЭМПИРИЧЕСКИЙ КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ

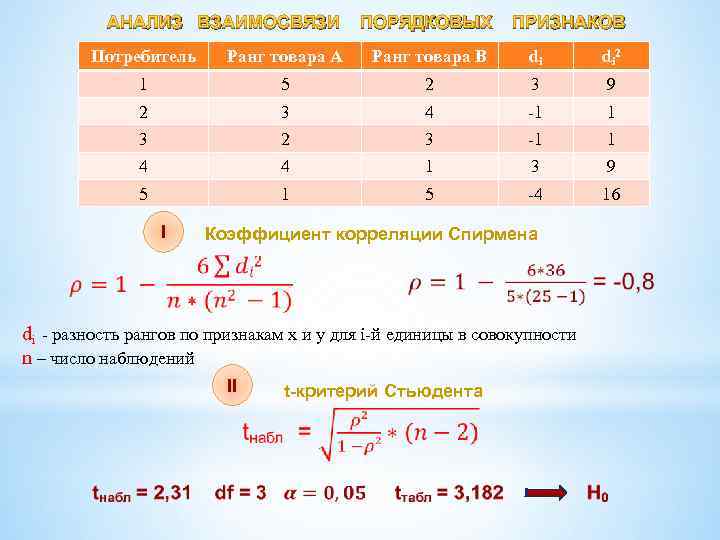АНАЛИЗ ВЗАИМОСВЯЗИ ПОРЯДКОВЫХ ПРИЗНАКОВ Потребитель Ранг товара А Ранг товара В di di 2 1 5 2 3 9 2 3 4 -1 1 3 2 3 -1 1 4 4 1 3 9 5 1 5 -4 16 I Коэффициент корреляции Спирмена di - разность рангов по признакам x и y для i-й единицы в совокупности n – число наблюдений II t-критерий Стьюдента

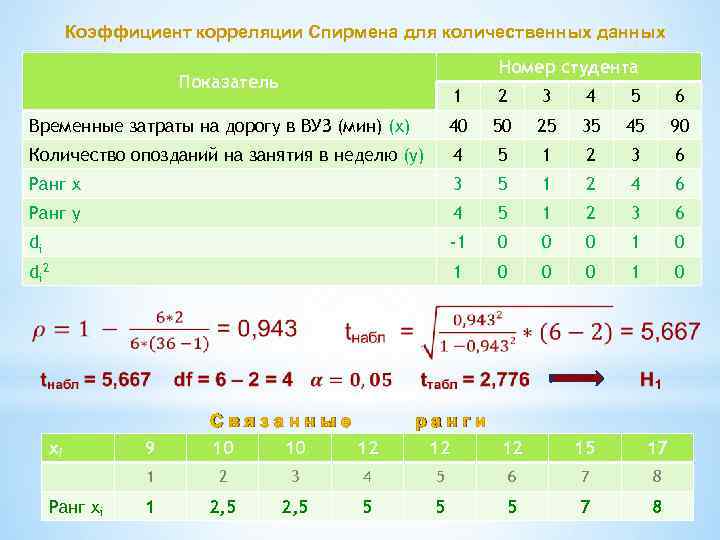Коэффициент корреляции Спирмена для количественных данных Номер студента Показатель 1 2 3 4 5 6 Временные затраты на дорогу в ВУЗ (мин) (x) 40 50 25 35 45 90 Количество опозданий на занятия в неделю (y) 4 5 1 2 3 6 Ранг x 3 5 1 2 4 6 Ранг y 4 5 1 2 3 6 di -1 0 0 0 1 0 di 2 1 0 0 0 1 0 xi 9 Связанные 10 10 12 ранги 12 12 15 17 1 Ранг xi 2 3 4 5 6 7 8 1 2, 5 5 5 5 7 8

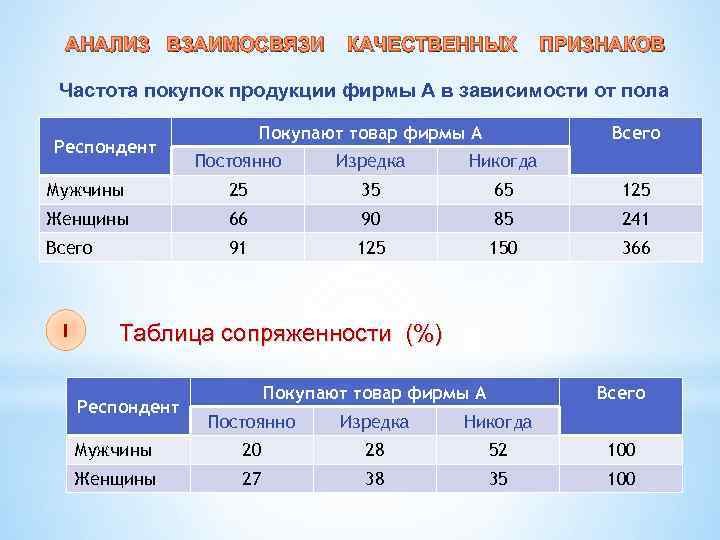АНАЛИЗ ВЗАИМОСВЯЗИ КАЧЕСТВЕННЫХ ПРИЗНАКОВ Частота покупок продукции фирмы А в зависимости от пола Респондент Покупают товар фирмы А Всего Постоянно Изредка Никогда Мужчины 25 35 65 125 Женщины 66 90 85 241 Всего 91 125 150 366 I Таблица сопряженности (%) Респондент Покупают товар фирмы А Всего Постоянно Изредка Никогда Мужчины 20 28 52 100 Женщины 27 38 35 100

II

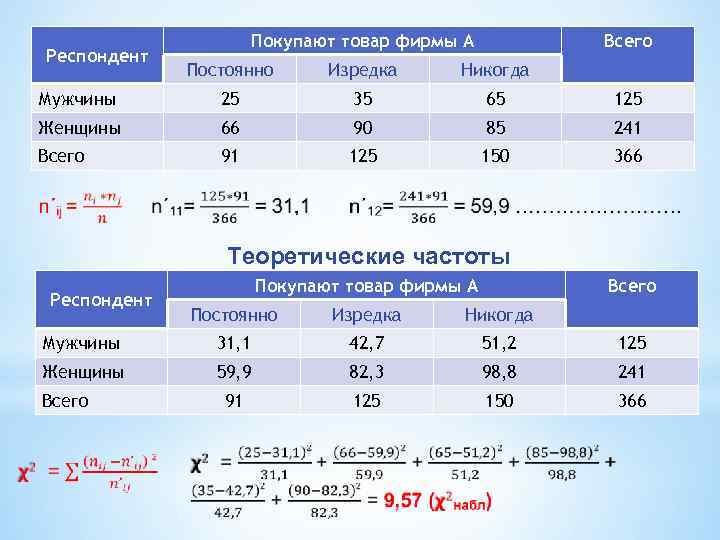Респондент Покупают товар фирмы А Всего Постоянно Изредка Никогда Мужчины 25 35 65 125 Женщины 66 90 85 241 Всего 91 125 150 366 Теоретические частоты Респондент Покупают товар фирмы А Всего Постоянно Изредка Никогда Мужчины 31, 1 42, 7 51, 2 125 Женщины 59, 9 82, 3 98, 8 241 91 125 150 366 Всего

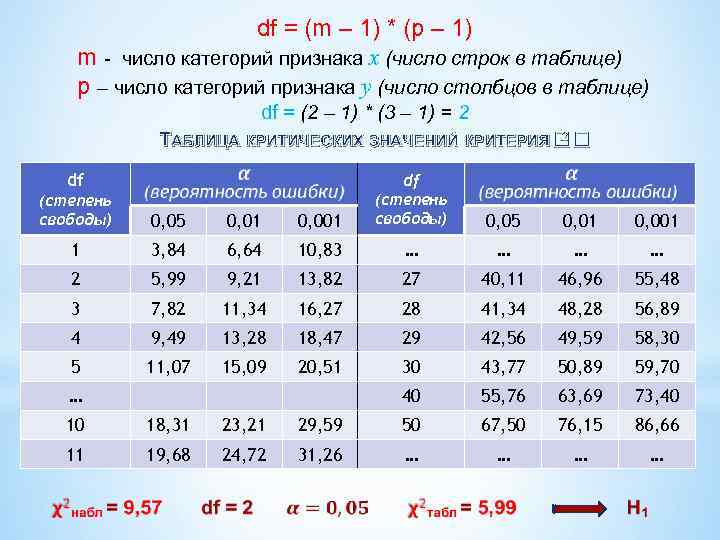df = (m – 1) * (p – 1) m - число категорий признака х (число строк в таблице) p – число категорий признака y (число столбцов в таблице) df = (2 – 1) * (3 – 1) = 2 2 ТАБЛИЦА КРИТИЧЕСКИХ ЗНАЧЕНИЙ КРИТЕРИЯ df (степень свободы) 0, 05 0, 01 0, 001 df (степень свободы) 1 3, 84 6, 64 10, 83 … … 2 5, 99 9, 21 13, 82 27 40, 11 46, 96 55, 48 3 7, 82 11, 34 16, 27 28 41, 34 48, 28 56, 89 4 9, 49 13, 28 18, 47 29 42, 56 49, 59 58, 30 5 11, 07 15, 09 20, 51 30 43, 77 50, 89 59, 70 40 55, 76 63, 69 73, 40 … 0, 05 0, 01 0, 001 10 23, 21 29, 59 50 67, 50 76, 15 86, 66 11 18, 31 19, 68 24, 72 31, 26 … …

СИЛА СВЯЗИ КАЧЕСТВЕННЫХ ПРИЗНАКОВ

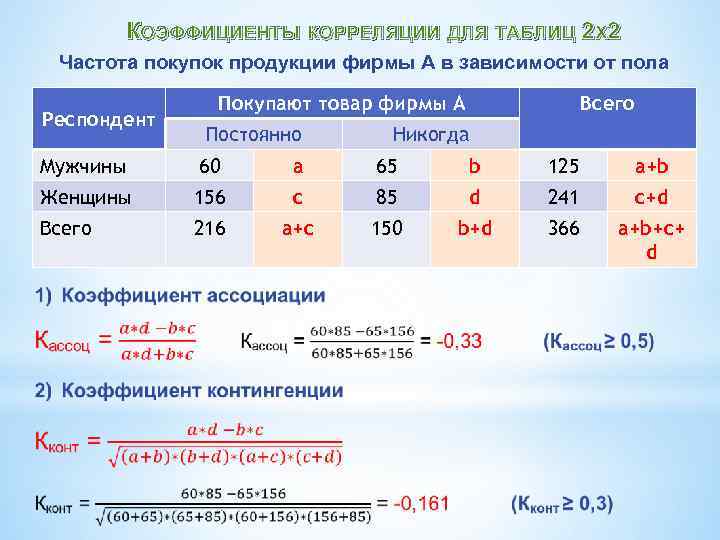КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ ДЛЯ ТАБЛИЦ 2 Х 2 Частота покупок продукции фирмы А в зависимости от пола Респондент Покупают товар фирмы А Постоянно Всего Никогда Мужчины a 65 b 125 a+b Женщины 156 c 85 d 241 c+d Всего 60 216 a+c 150 b+d 366 a+b+c+ d

РЕГРЕССИОННЫЙ АНАЛИЗ

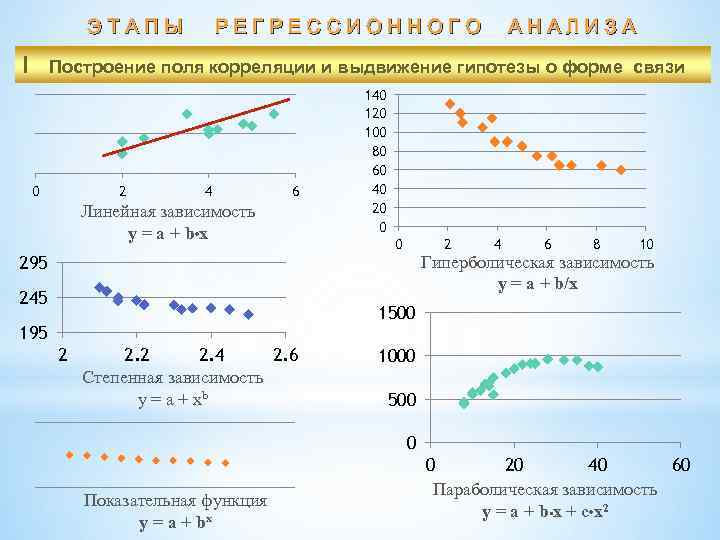Э Т А П Ы Р Е Г Р Е С С И О Н Н О Г О А Н А Л И З А I Построение поля корреляции и выдвижение гипотезы о форме связи 0 2 4 6 Линейная зависимость y = a + b • x 140 120 100 80 60 40 20 0 0 2 6 8 10 Гиперболическая зависимость y = a + b/x 295 245 4 1500 195 2 2. 4 2. 6 Степенная зависимость y = a + xb 1000 500 0 Показательная функция y = a + bx 0 20 40 60 Параболическая зависимость y = a + b • x + c • x 2

II Оценка параметров предполагаемого уравнения регрессии III Ø Ø IV Интерпретация полученных результатов Интерпретация-прогноз Интерпретация по оцениваемым параметрам Интерпретация по эластичности Интерпретация коэффициента детерминации Оценка статистической значимости коэффициента корреляции Ø Альтернативные гипотезы (H 0, H 1) Ø Наблюдаемое значение F-критерия Фишера (Fнабл) Ø Сравнение Fнабл и Fтабл (Fнабл < Fтабл H 0 Fнабл > Fтабл H 1 )

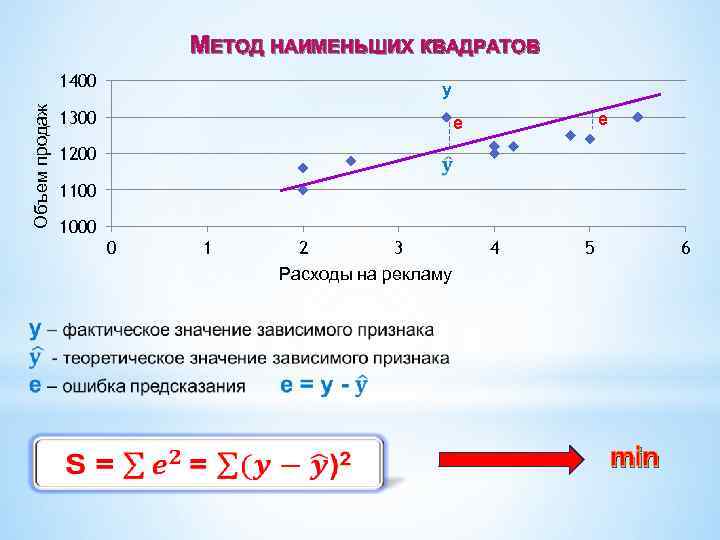МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Объем продаж 1400 y 1300 e e 1200 1100 1000 0 1 2 3 Расходы на рекламу 4 5 6 min

УРАВНЕНИЕ ЛИНЕЙНОЙ РЕГРЕССИИ Рекламный бюджет и объемы продаж предприятия А Расходы на рекламу (тыс. руб/мес) y = a + b • x Объем продаж (шт/мес) х y 2, 0 1 160 2, 0 1 100 2, 5 1300 4, 0 1 220 4, 0 1 200 4, 2 1 220 4, 8 1 250 5, 0 1 240 5, 5 1 300 1 180 3, 5 rxy – линейный коэффициент корреляции

И Н Т Е Р П Р Е Т А Ц-И Я О Г Н О З ПР -⅓ R xmin Xmax +⅓ R Расход на рекламу x= 3 Ожидаемый спрос на продукцию в среднем на уровне y = 1071, 3 + 38, 9 • 3 = 1188 ИНТЕРПРЕТАЦИЯ ОЦЕНИВАЕМЫМ РАМЕТРАМ ПО ПА b>0 – связь между признаками прямая b<0 – связь между признаками обратная b – величина изменения признака y (в единицах измерения y) при увеличении признака x на 1 ед. (в единицах измерения x) a>0 Vx>Vy a – среднее значение y при x=0 a<0 Vx

1% ИНТЕРПРЕТАЦИЯ ЭЛАСТИЧНОСТИ ПО Х E% Y Функции y = a + b • x Линейная y = a + b/x Коэффициент эластичности Гипербола y = a + b • x + c • x 2 Парабола y = a + xb Степенная y = a + bx Показательная E=b

ИНТЕРПРЕТАЦИЯ ЭФФИЦИЕНТА ТЕРМИНАЦИИ КО ДЕ 0 < R 2 < 100 Доля вариации результативного признака, которая объясняется вариацией факторных признаков Средняя ошибка аппроксимации < 5 -7% Отклонение прогнозируемых значений результирующего признака от фактического уровня

Оценка статистической значимости уравнения регрессии R 2 – коэффициент детерминации k – число независимых переменных в модели регрессии n – объем выборки F табл Степени свободы Fнабл < Fтабл H 0 Fнабл > Fтабл H 1

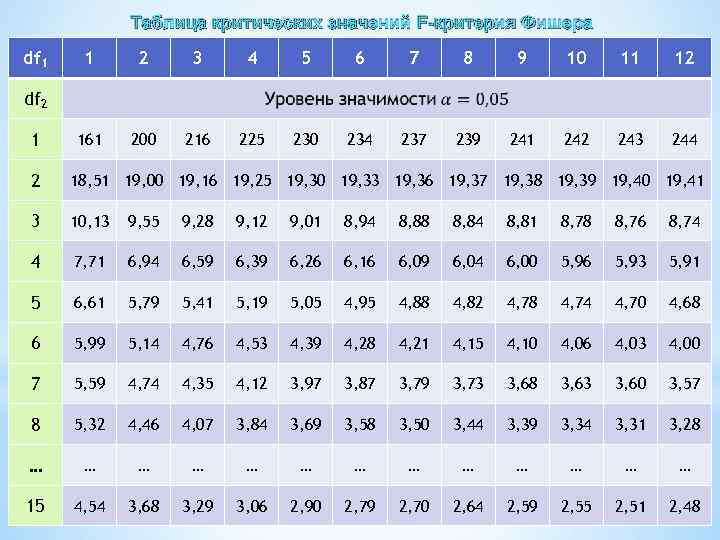Таблица критических значений F-критерия Фишера df 1 1 2 3 4 5 6 7 8 9 10 11 12 161 200 216 225 230 234 237 239 241 242 243 244 df 2 18, 51 19, 00 19, 16 19, 25 19, 30 19, 33 19, 36 19, 37 19, 38 19, 39 19, 40 19, 41 3 10, 13 9, 55 9, 28 9, 12 9, 01 8, 94 8, 88 8, 84 8, 81 8, 78 8, 76 8, 74 4 7, 71 6, 94 6, 59 6, 39 6, 26 6, 16 6, 09 6, 04 6, 00 5, 96 5, 93 5, 91 5 6, 61 5, 79 5, 41 5, 19 5, 05 4, 95 4, 88 4, 82 4, 78 4, 74 4, 70 4, 68 6 5, 99 5, 14 4, 76 4, 53 4, 39 4, 28 4, 21 4, 15 4, 10 4, 06 4, 03 4, 00 7 5, 59 4, 74 4, 35 4, 12 3, 97 3, 87 3, 79 3, 73 3, 68 3, 63 3, 60 3, 57 8 5, 32 4, 46 4, 07 3, 84 3, 69 3, 58 3, 50 3, 44 3, 39 3, 34 3, 31 3, 28 … … … … 15 4, 54 3, 68 3, 29 3, 06 2, 90 2, 79 2, 70 2, 64 2, 59 2, 55 2, 51 2, 48

Рекламный бюджет и объемы продаж предприятия А Расходы на рекламу (тыс. руб/мес) Объем продаж (шт/мес) х y 2, 0 1 160 2, 0 1 100 2, 5 1 180 3, 5 1300 4, 0 1 220 4, 0 1 200 4, 2 1 220 4, 8 1 250 5, 0 1 240 5, 5 1 300 Fнабл > Fтабл =5, 32 H 1