СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВАРИАЦИИ Тема 4 1 Вопросы

СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВАРИАЦИИ Тема 4 1

Вопросы: 1. Понятие вариации признаков. Система показателей вариации и порядок их расчета 2. Дисперсия, ее математические свойства и методы расчета 3. Дисперсия альтернативного признака 4. Виды дисперсий. Правило сложения дисперсий и его использование в анализе связей 2

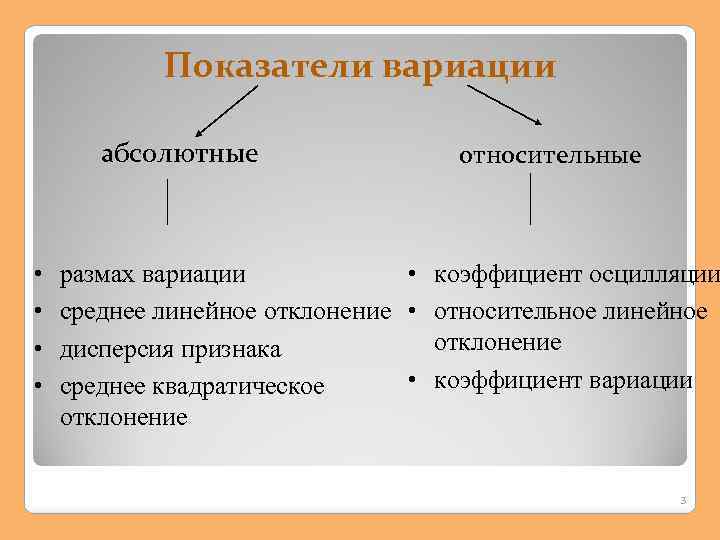Показатели вариации абсолютные • • относительные размах вариации • коэффициент осцилляции среднее линейное отклонение • относительное линейное отклонение дисперсия признака • коэффициент вариации среднее квадратическое отклонение 3

Абсолютные показатели вариации 1. Размах вариации 2. Среднее линейное отклонение 3. Дисперсия 4. Среднее квадратическое отклонение 4

Относительные показатели вариации 1. Коэффициент осцилляции 2. Линейный коэффициент вариации 3. Коэффициент вариации 5

ПРИМЕР 1. Имеются условные данные о распределении банков по величине уставного капитала Группы банков по величине уставного капитала (ден. ед. ) Число банков До 700 -1200 -1700 -2200 -2700 и выше итого 3 11 35 30 15 6 100 Середина интервала (х) 450 950 1450 1950 2450 2950 6

Расчет показателей вариации 1. Размах вариации 2. Среднее линейное отклонение 7

Расчет показателей вариации 3. Дисперсия 4. Среднее квадратическое отклонение 5. Коэффициент вариации 8

ПРИМЕР 2. Известны текущие оценки двух студентов. Сравнить степень вариации полученных оценок Оценки (х) 1 студент 3 7 2 студент 4 6 Средний балл Дисперсия Среднее квадратическое отклонение Коэффициент вариации 9

Математические свойства дисперсии 1. если все значения признака (варианты) уменьшить или увеличить на одно и то же постоянное число, то дисперсия от этого не изменится 3, 4, 10, 2 Все значения увеличиваем на 5. Получаем 8, 9, 15, 7. Средняя тоже увеличивается на 5. 10

Математические свойства дисперсии 2. если все значения признака уменьшить или увеличить в одно и то же число раз k, то дисперсия уменьшится или увеличится в k 2 раз. 3, 4, 10, 2 Все значения увеличиваем в 2 раза. Получаем 6, 8, 20, 4. Средняя тоже увеличивается в 2 раза. 11 (это то же самое, что 9, 6875 умножить на 4, т. е. на 2 в квадрате)

Математические свойства дисперсии 3. дисперсия, рассчитанная для любой постоянной величины А, будет всегда больше дисперсии, рассчитанной от средней, на квадрат разности между средней арифметической и этим числом А. 12

Математические свойства дисперсии 4. если величина А=0, то дисперсия будет равна разности между средним квадратическим значением признака и квадрата средней. Упрощенный способ расчета дисперсии - для несгруппированных данных - для сгруппированных данных 13

Математические свойства дисперсии ПРИМЕР. 3, 4, 10, 2 упрощенный способ: = 4, 752 = 22, 5625 Дисперсия 14

ПРИМЕР Определить среднее значение признака, если известно, что среднеквадратическое отклонение составляет 10, а средний квадрат признака равен 2804. упрощенный способ: 15

Дисперсия альтернативного признака Р – доля единиц, обладающих изучаемым признаком q – доля единиц, не обладающих изучаемым признаком 1 – наличие признака 0 – отсутствие признака р+q=1 р=1 -q q=1 -p 16

Расчет среднего значения альтернативного признака Признак Наличие (х) признака (f) Наличие признака 1 Отсутствие признака x·f 0 Итого 1 р 17

Расчет дисперсии альтернативного признака (х) (f) Наличие признака 1 р Отсутствие признака 0 q итого 1 18

ПРИМЕР 3. В результате контроля качества на заводе при выемке 1000 готовых изделий 20 оказались бракованными. Определить дисперсию бракованных изделий Доля брака : Дисперсия альтернативного признака: 19

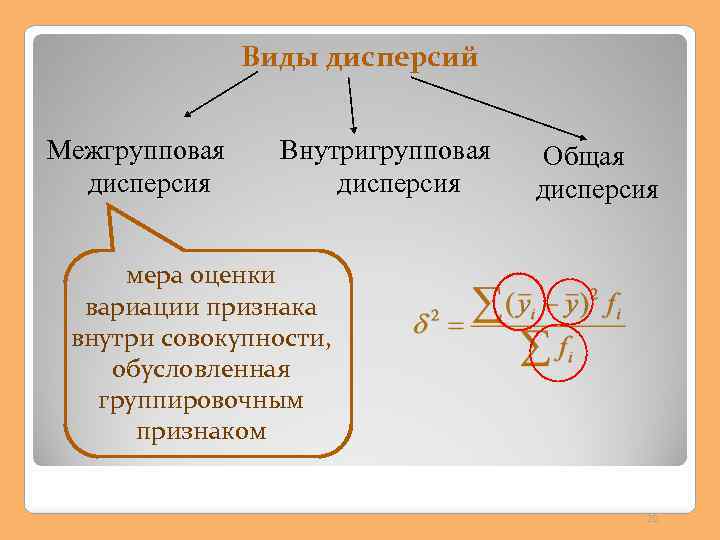Виды дисперсий Межгрупповая дисперсия Внутригрупповая дисперсия Общая дисперсия мера оценки вариации признака внутри совокупности, обусловленная группировочным признаком 20

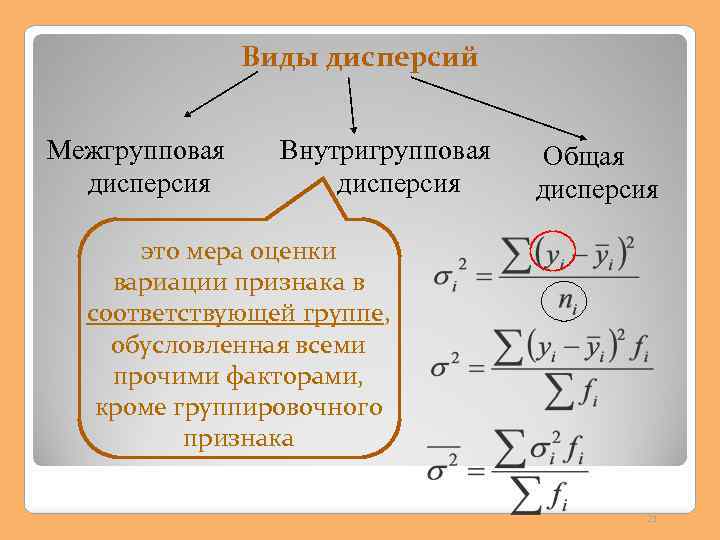Виды дисперсий Межгрупповая дисперсия Внутригрупповая дисперсия Общая дисперсия это мера оценки вариации признака в соответствующей группе, обусловленная всеми прочими факторами, кроме группировочного признака 21

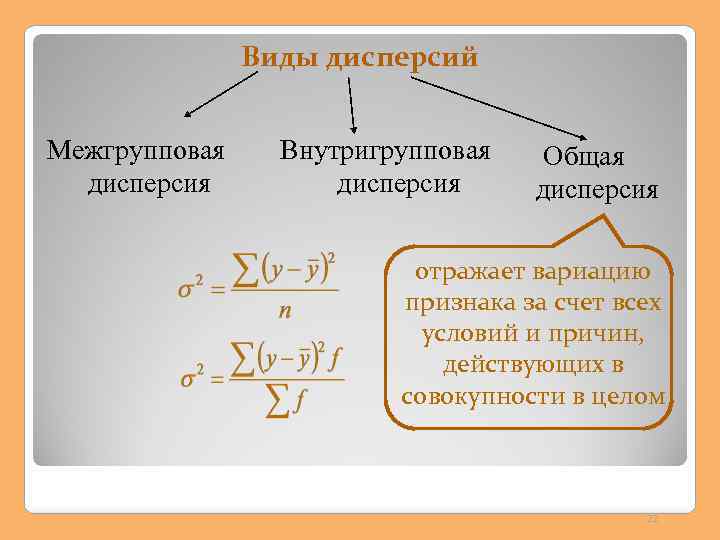Виды дисперсий Межгрупповая дисперсия Внутригрупповая дисперсия Общая дисперсия отражает вариацию признака за счет всех условий и причин, действующих в совокупности в целом 22

Правило сложения дисперсий 23

Показатели тесноты связи Коэффициент детерминации Эмпирическое корреляционное отношение Критерии оценки 0, 1 -0, 3 – связь слабая 0, 3 -0, 5 – связь умеренная 0, 5 -0, 7 – связь заметная 0, 7 -0, 9 – связь сильная 0, 9 и выше – весьма сильная 24

ПРИМЕР 4. Имеются условные данные о турах по Испании Местоположение Число турис- Средняя цена курорта тических недельного фирм тура, долл. Дисперсия цен туров в группе Коста-Брава 7 528, 57 2728, 04 Коста-дель-Соль 6 588, 33 8851, 14 Средняя цена недельного тура по всем фирмам 25

Межгрупповая дисперсия Средняя из внутригрупповых дисперсий Общая дисперсия Коэффициент детерминации Эмпирическое корреляционное отношение 26