Статистический анализ выборочных данных
Статистическая совокупность, которая включает в себя все изучаемые единицы, называется генеральной совокупностью. Метод статистического анализа, при котором изучаются не все единицы генеральной совокупности, а лишь ее часть, называется выборочным методом. Часть генеральной совокупности, в которую тем или иным способом отобраны отдельные статистические единицы, называется выборкой.
Свойство выборки правильно отображать, представлять состав генеральной совокупности называется репрезентативностью выборки.
Стандартная ошибка среднего значения выборки Стандартная ошибка относительного показателя Ϭ – среднеквадратическое отклонение f – относительный показатель в % n – объем выборки
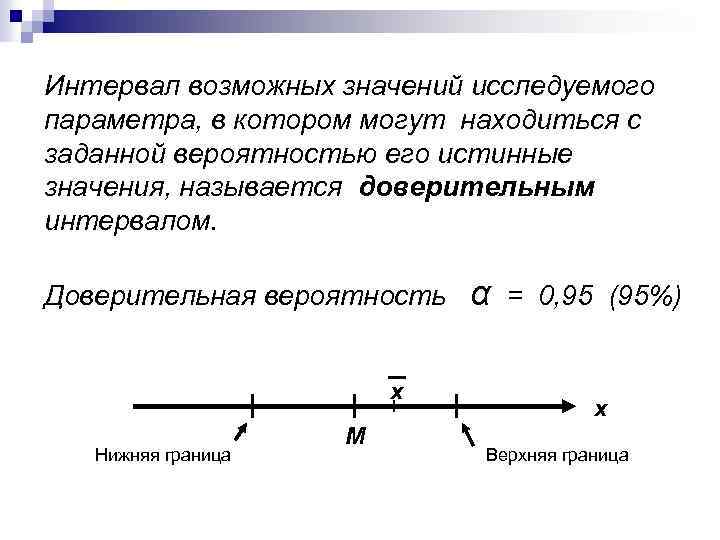
Интервал возможных значений исследуемого параметра, в котором могут находиться с заданной вероятностью его истинные значения, называется доверительным интервалом. Доверительная вероятность x Нижняя граница M α = 0, 95 (95%) x Верхняя граница
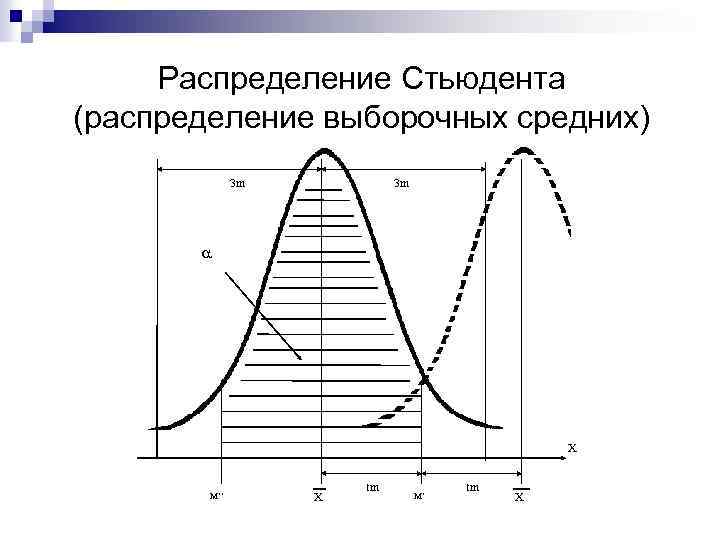
Распределение Стьюдента (распределение выборочных средних) 3 m 3 m X M’’ Х tm M’ tm Х
С увеличением доверительной вероятности величина доверительного интервала также увеличивается. n Коэффициент Стьюдента зависит от доверительной вероятности и объема выборки: t (α, n) n При α = 0, 95 и n>30 t ~ 2 n M-t*m Нижняя граница x M M+t*m x Верхняя граница
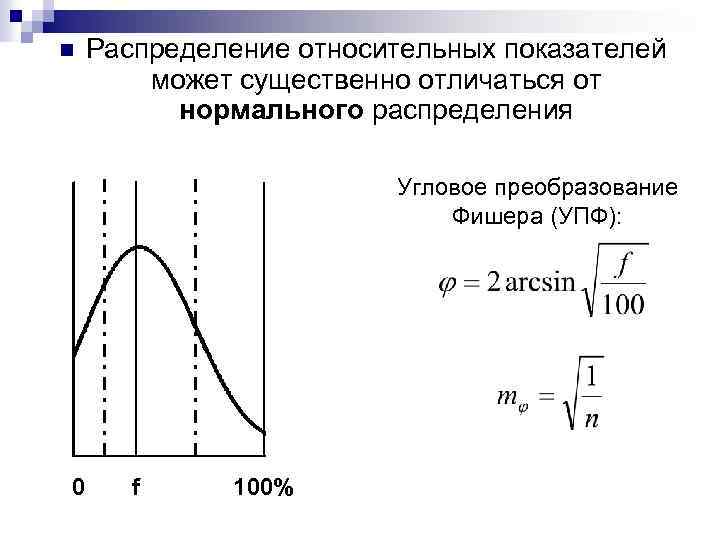
n Распределение относительных показателей может существенно отличаться от нормального распределения Угловое преобразование Фишера (УПФ): 0 f 100%
Статистическая проверка гипотез
Предположение об отсутствии существенных различий между сравниваемыми выборками называется нулевой гипотезой, противоположное предположение (о наличии существенных различий) альтернативной гипотезой. n Одна из гипотез должна быть обоснованно принята (как истинная), другая гипотеза – отвергнута. n
n n n Статистическая значимость различия двух выборок оценивается вероятностью ошибочного отклонения нулевой гипотезы. В большинстве медико-биологических исследований для вывода о статистической значимости различия двух выборок задается граница вероятности ошибочного отклонения нулевой гипотезы p< 0, 05 (5%) Если значимость расчетного критерия p> 0, 05, то принимается нулевая гипотеза, в противном случае (если значимость критерия p<0, 05) может быть принята альтернативная гипотеза.
k<d - область принятия k>d - область отклонения нулевой гипотезы d d d k k k 0 p= 0. 05 ОДНОСТОРОННИЙ КРИТЕРИЙ 0. 025 k 0 0. 025 ДВУСТОРОННИЙ КРИТЕРИЙ
n n Статистические критерии, основанные на предположении о нормальности распределения исследуемых выборок, называются параметрическими Статистический критерий для принятия гипотезы об отсутствии различий средних значений двух выборок, подчиняющихся нормальному закону, называется критерием Стьюдента. T < t( , n)
n Статистический критерий для принятия гипотезы об отсутствии различий дисперсий двух выборок, подчиняющихся нормальному закону, называется критерием Фишера. F < F( , n 1 -1, n 2 -1) F=D 1/D 2 если D 1>D 2 F=D 2/D 1 если D 2>D 1
n n Основное преимущество непараметрических критериев по сравнению с параметрическими состоит в том, что они могут быть использованы при распределениях выборок, отличающихся от нормального закона. Степень отличия формы распределения случайной величины от формы нормального или любого другого распределения оценивается по значению критерия хи -квадрат. 2 < 2 ( , r-3)
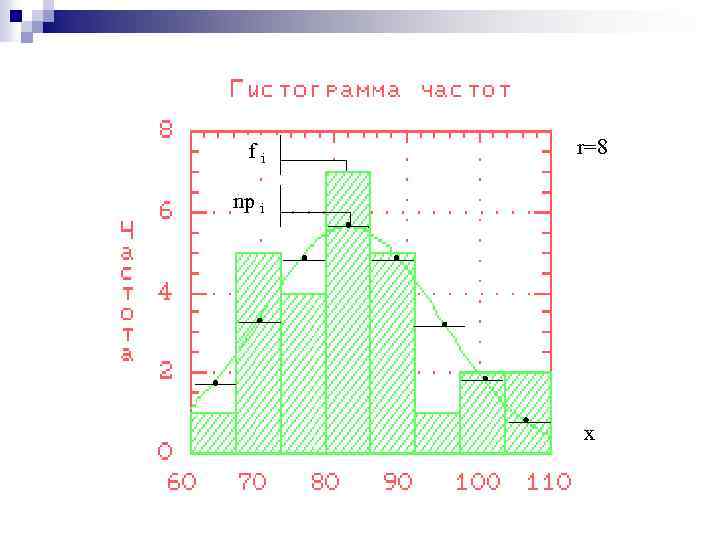
fi r=8 np i х
Значимость 3, 3 Е-04 = 3, 3*10 -4
Скачать презентацию Статистический анализ выборочных данных Статистическая совокупность которая
ЛЕКЦИЯ 3 Анализ выборочных данных.ppt