Статистические системы А а B b C c Все характеристики

Статистические системы А=а B=b C=c … Все характеристики системы известны и постоянны во времени Для получения полного описания достаточно средств квантовой механики Изолированная система в стационарном состоянии

А=? B=? C=? … Система в контакте с окружающей средой (характеристики системы могут изменяться непредсказуемым и неконтролируемым образом)

Флуктуации значений наблюдаемых Е Е 6 Е 5 Е 4 Е 3 Е 2 Е 1 Е 0 t

А 1, А 2, … , А n Статистический ансамбль P 1, P 2, … , P n ( А 1, А 2, … , Аn ) — спектр ( P 1, P 2, … , Pn ) — функция распределения Постулат: игральная кость симметрична и, следовательно, все вероятности одинаковы А 1, А 2, … , А n P 1, P 2, … , P n = 1, 2, 3, 4, 5, 6 1/ 6 1/ 6

Канонический ансамбль «Термостатированные» системы Энергия E ≠ const Число частиц N = const + Е – Е

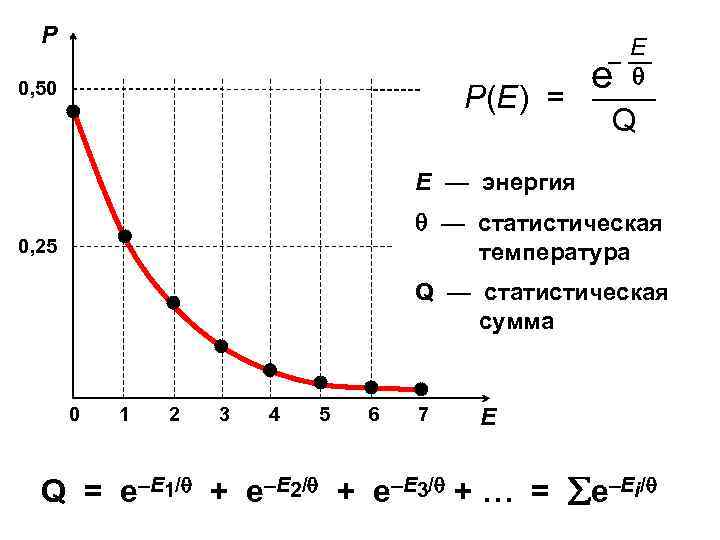
Р E –— е 0, 50 Р(Е) = —— Q E — энергия — статистическая температура 0, 25 Q — статистическая сумма 0 1 2 3 4 5 6 7 Е Q = е–Е 1/ + е–Е 2/ + е–Е 3/ + … = е–Еi/

Статистические суммы Статистическая сумма Q (или сумма по состояниям) — важнейший параметр модели КАНОНИЧЕСКОГО АНСАМБЛЯ, которая применяется при описании систем, находящихся в термическом контакте с термостатом. Е Е 3 Е 2 Р 2 Е 1 k Р 3 Р 1 Вероятность обнаружить термостатированную систему в состоянии с энергией Е E –— θ Р(Е) = е —— Q θ = k. T — статистическая температура = 1, 37 10– 23 Дж/K — постоянная Больцмана

Через статистическую сумму можно выразить все основные термодинамические характеристики системы: свободная энергия F = – k. T ln Q внутренняя энергия U = энтропия и др. (k. T)2 d (ln Q) ———— d (k. T) d (k. T ln Q) S = k —————— d (k. T)

Мультипликативность — если в сложной системе можно выделить несколько подсистем q 1 q 2 … … qn Q то статистическая сумма системы может быть представлена в виде произведения статистических сумм ее подсистем: Q = q 1 q 2 … qn Q 1 моль газа = ( qмолекулы ) NA Q молекулы = qпост. qвращ. qколеб.

Соглашение: при вычислении статистических сумм следует пользоваться специальной шкалой энергии — СТАТИСТИЧЕСКОЙ ЕКМ Еi = R n 2 0 ЕСтат Еi = R (n 2 – 1) 0 R = 2 2/2 m. L , n — квантовое число (номер уровня)

Q = е–Е 1/ + е–Е 2/ + е–Е 3/ + … = = 1 + е–Е 2/ + е–Е 3/ + … = 1 + е–Еi/ i=2 1< Q < N 1 1 P 1 = —– N Q = —– N 1 Q Число систем КА на нижнем уровне Общее число систем КА — мера статистичности системы (степени влияния термостата)

ПОСТУПАТЕЛЬНОЕ движение атомов и молекул (модель «частица в потенциальном ящике» ) (En)стат = En – Е 1 = ( 2 2/2 m. L 2) (n 2 – 1) Qt = 1 + [exp(– En / )] , где n = 2, 3, 4, … Qt = Qx Qy Qz Система: атом 4 Не в кубическом ящике с ребром L

L (нм) 0, 5 1 2 3 … 30 31 0 1, 000 … 1, 000 1 1, 003 1, 643 9, 000 30, 96 … 38 924 43 022 2 1, 086 3, 443 25, 67 91, 73 … 111 424 123 060 3 1, 306 5, 930 48, 63 172, 8 … 205 797 227 204 … … … … 30 23, 30 204, 3 1 776 6 199 … 6, 62 106 7, 30 106 31 24, 52 214, 9 1 870 6 518 … 6, 95 106 7, 67 106 Т (K)

2 m k. T Qt = —————– L h При больших L и Т Q Q Т = const L L = const T Влияние массы атома Qt (H) < Qt (He) < Qt (Ne) < Qt (Ar) < Qt (Kr) < …

Влияние массы частицы E 2 2 n 2 En = ——– 2 2 m. L E n = 3 n = 2 n = 1 Молекула Н 2 n = 1 Молекула D 2 n = 1 Молекула T 2

ВРАЩАТЕЛЬНОЕ движение молекул Qr = 1 + [ gm exp(– Em / ) ] (m = 1, 2, 3, …) Для плоского ротатора Em = b m 2 и gm = 2 ( b = 2 / I — вращательная постоянная ) При больших Т : Qr = k. T / b «число симметрий» (порядок оси вращения) =2 =6

Т = 300 K Молекула H—H H — Cl C=O I—I b / k. T Qr 0, 3 0, 05 0, 0002 2, 118 4, 463 13, 033 60, 382 Р Р Н 2 I 2 Е Восприимчивость вращательных степеней свободы молекулы к воздействию термостата возрастает с увеличением ее момента инерциии Е

КОЛЕБАТЕЛЬНОЕ движение молекул Qv = 1 + [ exp(– Ev / ) ] ( v = 1, 2, 3, …) Для одномерного гармонического осциллятора Ev = ω v (ω — собственная частота ) Т = 300 K Молекула H—H H — Cl C=O I—I ω / k. T 22 12, 5 10 1, 0 Qv 1 1, 000004 1, 000045 1, 582

Восприимчивость колебательных степеней свободы молекулы к воздействию термостата возрастает с уменьшением собственной частоты ω2 = k / Влияние масс колеблющихся атомов Qv (H 2) < Qv (D 2) < Qv (T 2) Влияние величины силовой константы Qv (N N) < Qv (O = O) < Qv (F – F)

Многомерный осциллятор Qv = (Qv)1 (Qv)2 (Qv)3 … (Qv)3 N – 6 Молекула циклогексана С 6 Н 12 имеет 48 колебательных степеней свободы Если для каждого НК одномерная сумма будет лишь незначительно отличаться от 1 (например, Qi = 1, 2), то полная колебательная сумма молекулы будет равна (1, 2)48 103, 8 6310. Чем сложнее состав и структура молекулы, тем более она восприимчива к воздействию окружающей среды (термостата)

ЭЛЕКТРОННЫЕ движения в молекулах Qэл = 1 (при Т < 1000 K) Исключение: сопряженные молекулы с длинной цепью сопряженных кратных связей (полиены, полиацетилен, графит и т. д. ) Q ( Е)e > ( Е)v > ( Е)r > ( Е)t Qe < Q v < Q r < Q t 1 t r v e E

Пример 1: электрон во внешнем магнитном поле Стационарное состояние | 1 Стационарное состояние | 2 E 1 = Eo – H E 2 = Eo + H Е Е 2 Еo Е 1 – Е 2 = 2 H = 1 10– 21 Дж H H В статистической шкале: Е 1 = 0 Е 2 = 1 10– 21 Дж

Состояние Ориентация векторов Энергия, Проекция Е, Дж. Sz z 1 (Н) (S) ( ) 0 – /2 + 2 (Н) (S) ( ) 1 10– 21 + /2 – Проекция Влияние термостата Е 2 Е Е 1 время

Неправильный вопрос (так как на него нельзя дать ответ) Чему равна энергия электрона? Правильный вопрос (можно дать ответ) Чему равна средняя по времени энергия электрона? Еt = Ea = P 1 E 1 + P 2 E 2 P 1 = exp[ –E 1/ ] / Q P 2 = exp[ –E 2/ ] / Q = ? Q = ?

T = 100 K = k. T = 1, 38 10– 21 Дж Q = 1 + exp[ –E 2/ ] E 2/ = 1 10– 21 / 1, 38 10– 21 = 1/1, 38 = 0, 7246 Q = 1 + exp[ – 0, 7246 ] = 1 + 0, 4845 = 1, 4845 P 1 = exp[ –E 1/ ] / Q = 1/1, 4845 = 0, 6736 P 2 = exp[ –E 2/ ] / Q = 0, 4845/1, 4845 = 0, 3264

Е = P 1 E 1 + P 2 E 2 = = 0, 6736 0 + 0, 3264 1 10– 21 = = 0, 3264 10– 21 Дж Sz = P 1 Sz 1 + P 2 Sz 2 = 0, 6736 (– /2) + + 0, 3264 (+ /2) = – 0, 1736 z = P 1 z 1 + P 2 z 2 = 0, 6736 (+ ) + + 0, 3264 (– ) = 0, 3472

Е, Дж Состояние 2 Макросостояние 1 10– 21 0, 3264 10– 21 (среднее) Состояние 1 Z SZ 0 + /2 – 0, 1736 – /2 +0, 3472 + /2

Многочастичные системы Пример 2: два электрона во внешнем магнитном поле Стационарное состояние | 11 Стационарное состояние |22 E 11 = Eo – 2 H E 12 = Eo + 2 H Стационарное состояние | 12 E 12 = Eo Стационарное состояние | 21 E 21 = Eo

Состояние Ориентация Энергия, векторов спина Проекция Е, Дж. Проекция Sz z 11 (S 1) (S 2) 0 – + 2 12 (S 1) (S 2) 1 10– 21 0 0 21 (S 1) (S 2) 1 10– 21 0 0 22 (S 1) (S 2) 2 10– 21 + – 2 Емех Естат E o + 2 H 4 H Eo 2 H E o – 2 H 0

Глобальная статистическая сумма Q = exp(–E 11/ ) + 2 exp(–E 12/ ) + exp(–E 22/ ) При 100 K: E 11 / = 0 E 12 / = E 21 / = 1 10– 21 / 1, 38 10– 21 = 0, 7246 E 22 / = 2 10– 21 / 1, 38 10– 21 = 1, 4492 Q = exp(– 0) + 2 exp(– 0, 7246) + exp(– 1, 4492) = = 1 + 2 0, 4845 + 0, 2347 = 2, 2037

Вероятности глобальных состояний Р 11 = 1 / 2, 2037 = 0, 4538 Р 12 = Р 21 = 0, 4845 / 2, 2037 = 0, 2198 Р 22 = 0, 2347 / 2, 2037 = 0, 1065 Среднее значение энергии E = E 11 P 11 + 2 E 12 P 12 + E 22 P 22 = = 0 0, 4538 + 2 1 10– 21 0, 2198 + 2 10– 21 0, 1065 = = 0, 6528 10– 21 [Дж]

Среднее значение проекции вектора спина Sz = Sz 11 P 11 + 2 Sz 12 P 12 + Sz 22 P 22 = = (– ) 0, 4538 + 2 0 0, 2198 + (+ ) 0, 1065 = = – 0, 3472 Среднее значение проекции вектора z = z 11 P 11 + 2 z 12 P 12 + z 22 P 22 = = (+2 ) 0, 4538 + 2 0 0, 2198 + (– 2 ) 0, 1065 = = – 0, 6944

Число частиц Q E , Дж Sz , 1 1, 4845 0, 3264 10– 21 – 0, 1736 0, 3472 2 2, 2037 0, 6528 10– 21 – 0, 3472 0, 6944 Q 2 = (Q 1)2 мультипликативность E 2 = 2 E 1 Sz 2 = 2 Sz 1 z 2 = 2 z 1 аддитивность

Рейф Ф. Статистическая физика (Берклеевский курс физики). М. : Наука, 1977. Киттель Ч. Статистическая термодинамика. М. : Наука. 1977. Домашнее задание Задача 5. 1. Сравнить по величине статистические суммы (поступательные Qt, вращательные Qr, колебательные Qv) для трех указанных молекул 1) расположить молекулы в ряд по возрастанию величины статистической суммы А В С Qt 2) дать пояснения причин именно такого расположения (массы, размеры и моменты инерции, прочности связей и частоты колебаний и т. д. ).

Задача 5. 2. Протон помещен во внешнее магнитное поле, вызывающее расщепление его спинового энергетического уровня на величину E = 2 H = 1 10– 22 Дж. Зная среднее значение проекции спина SZ, вычислить: 1) статистическую сумму Q (в статистической шкале), 2) температуру термостата (в кельвинах), 3) среднюю магнитную энергию (в джоулях). k = 1, 38 10– 23 ; E 1 = – 5 10– 23 Дж ; Q = 1 + ехр [–(E 2 – E 1) / k. T ] ; P 1 = 1/Q ; P 2 = 1 – P 1 E = E 1 P 1 + E 2 P 2 SZ = (– 1/2) P 1 + (+1/2) P 2 E 2 = 5 10– 23 Дж

Задача 5. 3. Для атома гелия (Не 4), находящегося в трехмерном потенциальном ящике с размерами LX = 3 нм, LY = 4 нм, LZ = 5 нм вычислить поступательную статистическую сумму: а) в статистической шкале (Qстат. ) б) в механической шкале (Qмех. ) ( ЕХi )стат. = R [ (n. Хi )2 – 1 ] ( Ехi )мех. = R (n. Хi )2 1000 QХ = 1 + е–Ехi / i=2 температура термостата указана в индивидуальных вариантах где R = 2 2/2 m. LХ 1000 QY = 1 + е–Еyi / i=2 1000 QZ = 1 + е–Еzi / i=2 Q = QX QY QZ