Статистические ряды распределения 1 Статистический ряд распределения

Статистические ряды распределения 1

Статистический ряд распределения – это групповая таблица, имеющая две графы: • группы по выделенному признаку (графа вариант) ; • численность групп (графа частот). Итак, ряд распределения представляет собой упорядоченное расположение единиц изучаемой совокупности по определенному группировочному признаку. 2

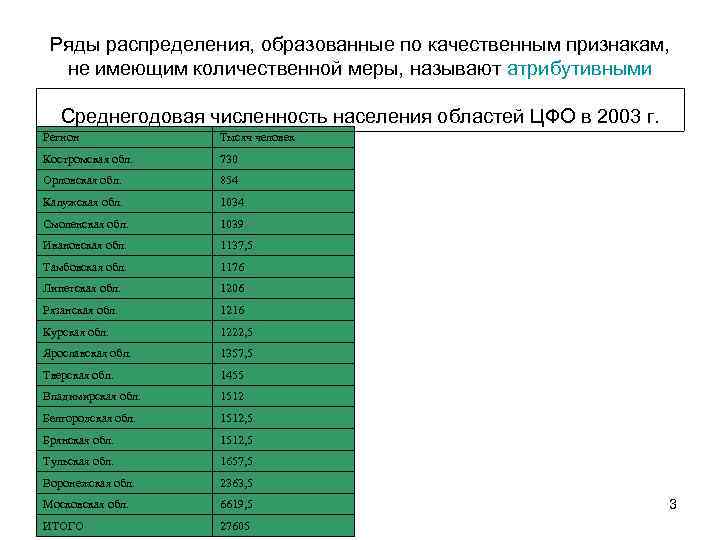Ряды распределения, образованные по качественным признакам, не имеющим количественной меры, называют атрибутивными Среднегодовая численность населения областей ЦФО в 2003 г. Регион Тысяч человек Костромская обл. 730 Орловская обл. 854 Калужская обл. 1034 Смоленская обл. 1039 Ивановская обл. 1137, 5 Тамбовская обл. 1176 Липетская обл. 1206 Рязанская обл. 1216 Курская обл. 1222, 5 Ярославская обл. 1357, 5 Тверская обл. 1455 Владимирская обл. 1512 Белгородская обл. 1512, 5 Брянская обл. 1512, 5 Тульская обл. 1657, 5 Воронежская обл. 2363, 5 Московская обл. 6619, 5 ИТОГО 27605 3

Ряды распределения, образованные по количественному признаку, называют вариационными. Вариационные ряды состоят из двух элементов: варианты и частоты. Варианта - это отдельное значение варьирующего признака, которое он принимает в ряду распределения, как правило, обозначается буквой хi. Частота - это численность вариант в группе вариационного ряда, обозначается fi. Сумма частот составляет объем совокупности (N). 4

ЧАСТОСТЬ или ОТНОСИТЕЛЬНАЯ ЧАСТОТА Частоты, выраженные в долях единицы, называются частостями, обозначаются обычно wi. Частости позволяют сопоставлять ряды с различным числом наблюдений. 5

НАКОПЛЕННАЯ ЧАСТОТА Накопленная частота (Si) – число единиц совокупности, имеющих значение признака не больше, чем Xi 6

ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ Абсолютная плотность распределения (p) – величина частоты, приходящаяся на единицу величины интервала: Pi=fi/hi Относительная плотность распределения : р’ = Wi/hi Показатели используются вместо частоты и частости, когда в интервальном ряду распределения интервалы неравные 7

Вариационные ряды делятся на дискретные, основанные на прерывной вариации признака, и интервальные, базирующиеся на непрерывно изменяющемся значении признака, принимающим любые количественные выражения. 8

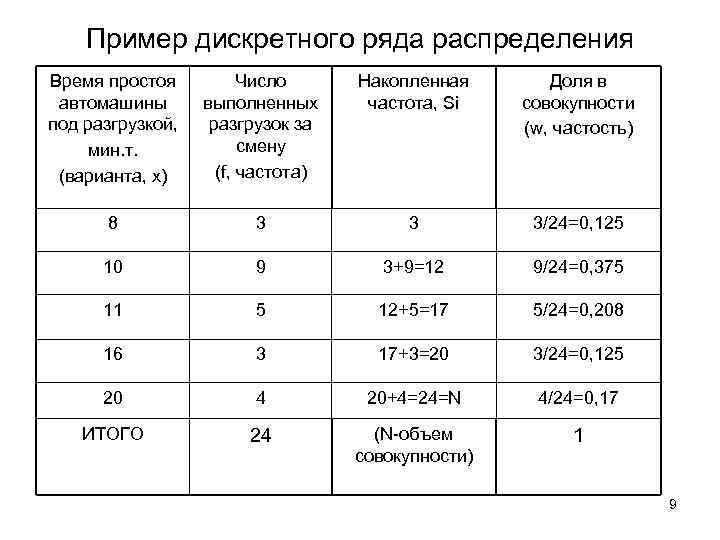Пример дискретного ряда распределения Время простоя автомашины под разгрузкой, мин. т. (варианта, х) Число выполненных разгрузок за смену (f, частота) Накопленная частота, Si Доля в совокупности (w, частость) 8 3 3 3/24=0, 125 10 9 3+9=12 9/24=0, 375 11 5 12+5=17 5/24=0, 208 16 3 17+3=20 3/24=0, 125 20 4 20+4=24=N 4/24=0, 17 ИТОГО 24 (N-объем совокупности) 1 9

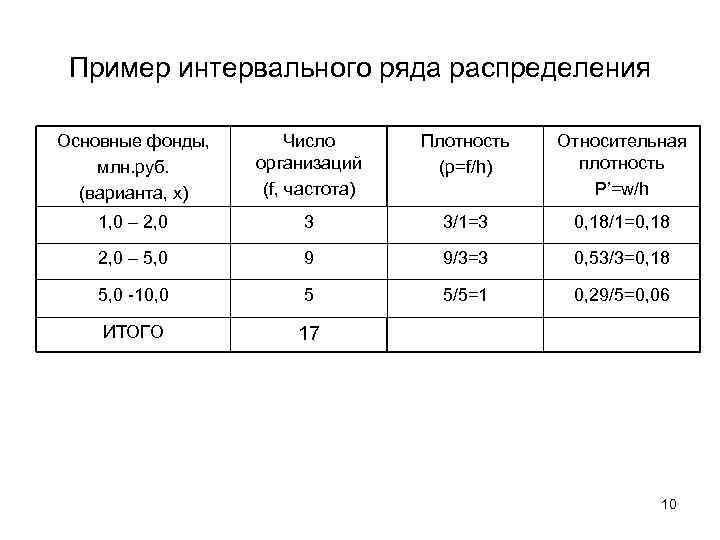Пример интервального ряда распределения Основные фонды, млн. руб. (варианта, х) Число организаций (f, частота) Плотность (р=f/h) Относительная плотность P’=w/h 1, 0 – 2, 0 3 3/1=3 0, 18/1=0, 18 2, 0 – 5, 0 9 9/3=3 0, 53/3=0, 18 5, 0 -10, 0 5 5/5=1 0, 29/5=0, 06 ИТОГО 17 10

Наглядно представляют ряды распределения с помощью графиков – полигона, гистограммы, кумуляты и огивы распределения признака в совокупности 11

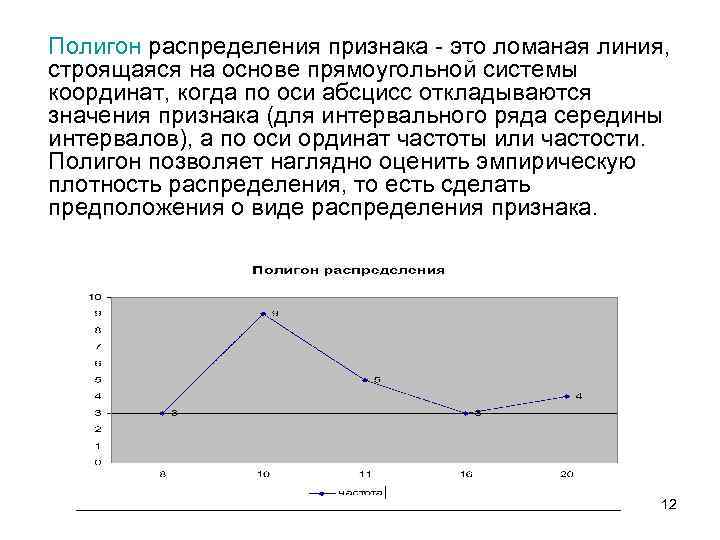Полигон распределения признака - это ломаная линия, строящаяся на основе прямоугольной системы координат, когда по оси абсцисс откладываются значения признака (для интервального ряда середины интервалов), а по оси ординат частоты или частости. Полигон позволяет наглядно оценить эмпирическую плотность распределения, то есть сделать предположения о виде распределения признака. 12

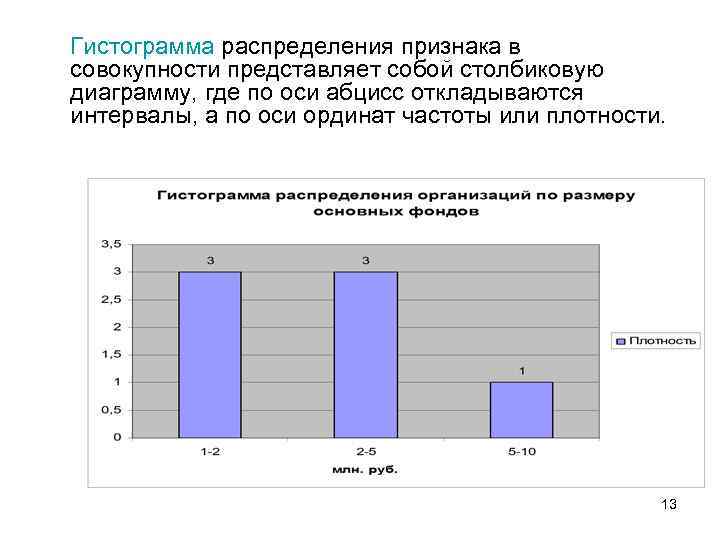Гистограмма распределения признака в совокупности представляет собой столбиковую диаграмму, где по оси абцисс откладываются интервалы, а по оси ординат частоты или плотности. 13

Кумулята (кумулятивная кривая) - это ломаная линия, строящаяся на основе прямоугольной системы координат, когда по оси абсцисс откладываются значения признака (для интервального ряда середины интервалов), а по оси ординат накопленные частоты или частости. Если на оси абсцисс отражать накопленные частоты, а на оси ординат значения признака, то полученная кривая носит название огивы распределения. 14

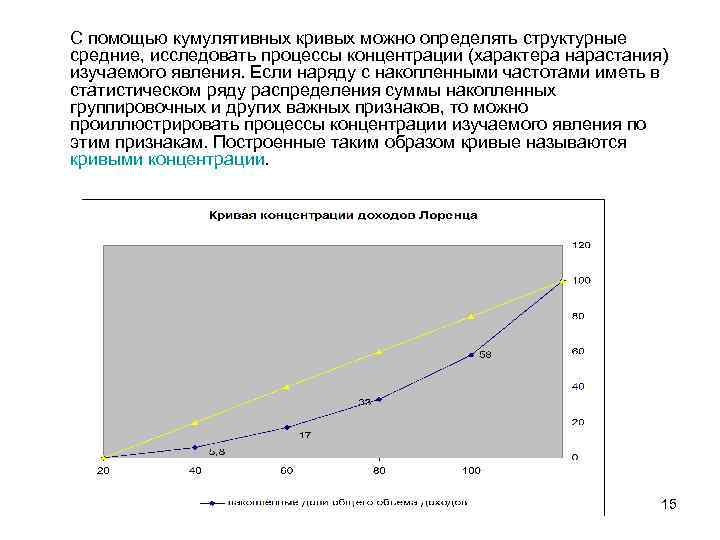С помощью кумулятивных кривых можно определять структурные средние, исследовать процессы концентрации (характера нарастания) изучаемого явления. Если наряду с накопленными частотами иметь в статистическом ряду распределения суммы накопленных группировочных и других важных признаков, то можно проиллюстрировать процессы концентрации изучаемого явления по этим признакам. Построенные таким образом кривые называются кривыми концентрации. 15

АНАЛИЗ РЯДОВ РАСПРЕДЕЛЕНИЯ • Показатели центра распределения (среднее, мода, медиана) • Показатели вариации (размах вариации, дисперсия, среднее линейное отклонение, среднее квадратичное отклонение, коэффициент вариации) • Показатели формы распределения (квартили, децили, перцентили, показатели дифференциации, ассиметрия, эксцесс, кривая распределения) 16

ПОКАЗАТЕЛИ ЦЕНТРА РАСПРЕДЕЛЕНИЯ 17

Среднее значение в дискретном ряду распределения 18

ПРИМЕР РАСЧЕТА СРЕДНЕГО ЗНАЧЕНИЯ ДИСКРЕТНОГО РЯДА РАСПРЕДЕЛЕНИЯ Возраст студента хi 18 Число человек fi 10 19 7 ИТОГО 17 В среднем (18*10+19*7)/17=18, 4 19

Среднее значение в интервальном ряду распределения 20

ПРИМЕР РАСЧЕТА СРЕДНЕГО ЗНАЧЕНИЯ ИНТЕРВАЛЬНОГО РЯДА РАСПРЕДЕЛЕНИЯ Возраст студента, хi Число человек Середина интервала х’ До 18 5 17 18 -20 10 19 ИТОГО 15 В среднем (17*5+19*10)/15=18, 3 21

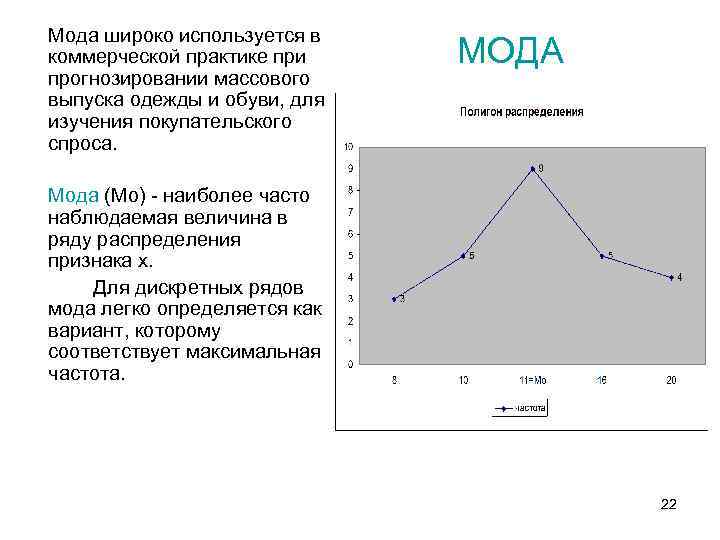Мода широко используется в коммерческой практике при прогнозировании массового выпуска одежды и обуви, для изучения покупательского спроса. МОДА Мода (Мо) - наиболее часто наблюдаемая величина в ряду распределения признака х. Для дискретных рядов мода легко определяется как вариант, которому соответствует максимальная частота. 22

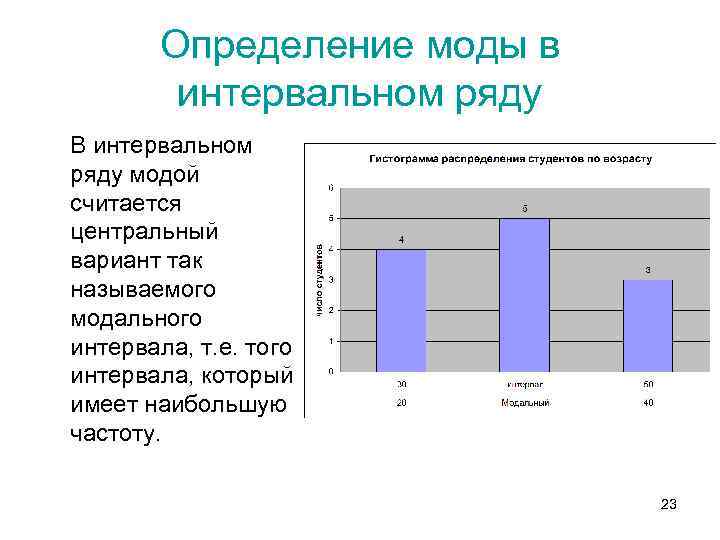Определение моды в интервальном ряду В интервальном ряду модой считается центральный вариант так называемого модального интервала, т. е. того интервала, который имеет наибольшую частоту. 23

При этом приближенное значение модальной величины признака для равно интервального ряда определяется по следующей формуле: где х0 - нижняя граница модального интервала; h - величина модального интервала; ƒm - частота модального интервала; ƒm+1 - частота интервала следующего за модальным интервалом. ƒm-1 - частота интервала предшествующего модальному интервалу. 24

МЕДИАНА Медиана (Me) - это величина, которая делит численность упорядоченного (ранжированного) вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньше или равно срединному варианту, а другая – больше или равные. Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда. Например, прогнозируемый экспертами период окончания строительства электростанции: 2 года 2 года 3 года 5 лет В качестве экспертной оценки всегда выбирается медианное значение, то есть 3 года. Для ранжированного ряда с четным числом членов медианой будет являться средняя арифметическая из двух смежных вариант. Например, прогнозируемый экспертами период окончания строительства электростанции: 2 года 2 года 3 года 5 лет Экспертная оценка (Ме) = (2+3)/2=2, 5 года 25

Медиана обладает свойством линейного минимума: сумма абсолютных значений отклонений величины признака у всех единиц совокупности от медианы минимальна, т. е. : 26

МОДА И МЕДИАНА В ДИСКРЕТНОМ РЯДУ Возраст студента хi Мо=18=Ме Число человек fi 19 7 Накопленная частота si 10>чем половина всех наблюдений 17 ИТОГО 17 17/2=8, 5 10=мах 27

Формула для определения медианы в равноинтервальном ряду распределения имеет вид: где х0 - нижняя граница медианного интервала; h- величина медианного интервала; ∑ƒ -сумма частот ряда; Sm-1 - сумма накопленных частот в интервалах, предшествующих медианному; ƒm - частота медианного интервала. 28

Мо и Ме в интервальном ряду Возраст студента, хi До 18 18 -20 Модальный и медианный интервалы ИТОГО Мо=18+2((10 -5)/((10 -5)+(100)))=18, 7 Число человек 5 Si 10=max 15>7, 5 15 - 5 Ме=18+2((7, 55)/10)=18, 5 29

НОРМАЛЬНЫЕ ДАННЫЕ Мо=Ме=среднему значению 30

ПОКАЗАТЕЛИ ВАРИАЦИИ РАСПРЕДЕЛЕНИЯ ПРИЗНАКА 31

ВАРИАЦИЯ Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Вариация возникает в результате того, что индивидуальные значения признака формируются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Влияющие факторы имеют либо случайный характер, либо систематический, в связи с этим различают случайную вариацию, сформированную случайными факторами, и систематическую вариацию, сформированную систематическими факторами. 32

Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Изучая силу и характер вариации в выделенной совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и в качественном отношении, а, следовательно, насколько характерной является исчисленная средняя величина, то есть насколько достоверными будут плановые и прогнозные расчеты. Для того чтобы измерить вариацию признака используют показатели (меры) вариации. 33

• Размах вариации (R) - абсолютная мера вариации признака, определяется как разность между наибольшим и наименьшим индивидуальными значениями признаков в совокупности: • Другим абсолютным показателем вариации является сумма квадратов отклонений (S): 34

Для более точного определения вариации используются средние величины: среднее линейное отклонение (d), дисперсия (σ²) и среднее квадратическое отклонение (σ). Среднее линейное отклонение характеризует среднюю ошибку (погрешность) в абсолютном выражении. Для сгруппированных данных рассчитывается среднее взвешенное линейное отклонение по формуле: Для сравнения вариации совокупностей данных, имеющих разные единицы измерения, используют относительную меру вариации безразмерную величину - дисперсию: 35

• Среднее квадратическое отклонение (σ) равно корню квадратному из дисперсии. Оно всегда больше среднего линейного отклонения, чем меньше среднее квадратическое отклонение, тем однороднее совокупность. • Дисперсия обладает рядом свойств, доказываемых в математической статистике, которые позволяют упростить ее расчеты. Если из всех значений вариант отнять какое-то постоянное число А, то дисперсия от этого не изменится. Если все значения вариант разделить на какое-то постоянное число А, то дисперсия уменьшится от этого в А 2 раз , а среднеквадратическое отклонение - в А раз. Дисперсия от средней имеет свойство минимальности, т. е. она всегда меньше дисперсий, исчисленных от любых других величин. Дисперсия равна разности среднего из квадратов и квадрата среднего: 1. 2. 3. 4. 36

• Для характеристики однородности совокупности по изучаемому признаку исчисляются относительные показатели вариации: коэффициент осцилляции, коэффициент вариации и относительное линейное отклонение. Они позволяют сравнивать характер рассеивания в различных распределениях. Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%. • Коэффициент осцилляции (К 0) отражает относительную вариацию крайних значений признака вокруг средней. 37

• Относительное линейное отклонение (V´) характеризует долю усредненного значения абсолютных отклонений от средней величины. • Коэффициент вариации (V) вычисляется по формуле: Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем колеблемости. Если коэффициент вариации меньше 33%, то изучаемая совокупность однородна по исследуемому признаку, следовательно, среднее значение может считаться состоятельной характеристикой типичного значения признака в совокупности. 38

ПОКАЗАТЕЛИ ФОРМЫ РАСПРЕДЕЛЕНИЯ 39

Величины, характеризующие разбиение частотного распределения на ряд равных частей, обычно называют квантилями, которые являются ранговыми характеристиками распределения. Помимо медианы, которая является квантилем по своей сути, из них наиболее широко применяются квартили (Q), разбивающие распределение частот на четыре равные части, децили (D)(на 10 равных частей) и процентили (P) (на 100 частей). 40

КВАРТИЛИ Квартилей всего три и Ме является вторым квартилем Q 2, так как делит совокупность данных 50% на 50% Первый квартиль Q 1 делит совокупность данных в соотношении 25% к 75% Третий квартиль Q 3 делит совокупность данных в соотношении 75% к 25% 41

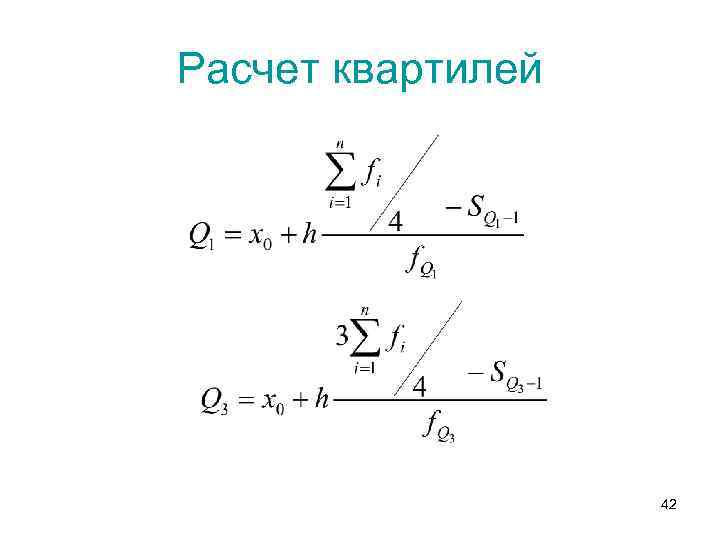Расчет квартилей 42

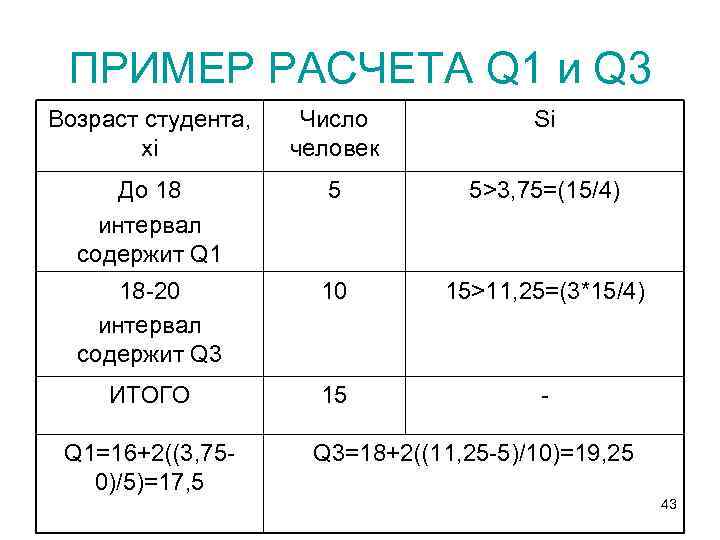ПРИМЕР РАСЧЕТА Q 1 и Q 3 Возраст студента, хi Число человек Si До 18 интервал содержит Q 1 5 5>3, 75=(15/4) 18 -20 интервал содержит Q 3 10 15>11, 25=(3*15/4) ИТОГО 15 - Q 1=16+2((3, 750)/5)=17, 5 Q 3=18+2((11, 25 -5)/10)=19, 25 43

Расчет децилей и персентилей 44

ПОКАЗАТЕЛИ (КОЭФФИЦИЕНТЫ) ДИФФЕРЕНЦИАЦИИ • Квартильная дифференциация KQ=Q 3/Q 1 • Децильная дифференциация КD=D 9/D 1 • Фондовая дифференциация Кф=(среднее из 10% наибольших величин)/(среднее из 10% наименьших величин) 45

АССИМЕТРИЯ Симметричность распределения признака характеризует коэффициент ассиметрии: As=μ 3/σ³, где μ 3 = центральный момент распределения 3 -го порядка σ³ - среднее квадратическое отклонение в кубе ЕСЛИ ДАННЫЕ НОРМАЛЬНЫЕ, ТО ЕСТЬ ПОДЧИНЯЮТСЯ РАСПРЕДЕЛЕНИЮ Гаусса, то они имеют симметричное распределение признака, когда As=0 или |As|/σAS<3, где σAS= 46

ЭКСЦЕСС ( «горб» ) Высоту «горба» распределения, его крутизну характеризует показатель эксцесса: Ех = (µ 4/σ где центральный момент )-3, распределения 4 -го порядка μ 4 = , σ дисперсия в квадрате ЕСЛИ ДАННЫЕ НОРМАЛЬНЫЕ, ТО ЕСТЬ ПОДЧИНЯЮТСЯ РАСПРЕДЕЛЕНИЮ Гаусса, то они имеют такой «горб» , когда Ех=0 ( µ 4/σ или |Ех|/σЕх<3, =3) где σЕх= 47

НОРМАЛЬНЫЕ ДАННЫЕ правило трех сигм ЕСЛИ В СОВОКУПНОСТИ ВСЕ ВАРИАНТЫ НАХОДЯТСЯ В ИНТЕРВАЛЕ , ТО ОНИ НОРМАЛЬНЫЕ 48

АНОМАЛЬНЫЕ ДАННЫЕ ВЫБРОСЫ ЕСЛИ В СОВОКУПНОСТИ ЕСТЬ ВАРИАНТЫ, КОТОРЫЕ НАХОДЯТСЯ ЗА ПРЕДЕЛАМИ ИНТЕРВАЛА , ТО ОНИ АНОМАЛЬНЫЕ 49