СТАТИСТИЧЕСКИЕ РАСЧЕТЫ В настоящее время

СТАТИСТИЧЕСКИЕ РАСЧЕТЫ

• В настоящее время методы, математической статистики, успешно применяются при ведении статистических исследований в психологии. MS Excel позволяет выполнять не только простые расчеты, основанные на арифметических операциях, но и сложные операции над данными, включая статистическую обработку информации, психологический анализ, прогнозирование и т. д. • При проведении статистических исследований собранная информация первоначально представляет собой набор несистематизированных данных. Например, анкетирование покупателей, социологические опросы, результаты переписи населения и т. п. дают наборы значений тех или иных признаков. Они фиксируются, на бумаге, а затем переносятся на машинные носители информации: магнитные диски, «флэшки» , компакт-диски, где сохраняются в виде файлов. При этом в подавляющем большинстве случаев наблюдения представляются в формате текстовых файлов, ЭТ и баз данных.

• В электронной форме информация может быть подвергнута любой вычислительной обработке, причем произвольное число раз и по различным алгоритмам, которые, в свою очередь, определяются целями и методикой исследования. Многие статистические величины могут быть вычислены непосредственно по собранной информации, без какой-либо предварительной подготовки, например без группировки данных

• Примечание: на результат вычислений влияет флажок Нулевые значения, который устанавливается/сбрасывается на вкладке Вид (команда Параметры, меню Сервис). В общем случае необходимо сбрасывать флажок, чтобы от нулей «не рябило в глазах» . При статистической обработке он всегда должен быть установлен, иначе нулевые значения будут просто пропущены, хотя, возможно, для изучаемого признака они являются допустимыми. Если не учесть данное свойство функций, то, очевидно, результаты расчетов будут неверными.

Статистические функции в Excel • Число наблюдений N • СЧЁТ • Подсчитывает количество чисел в списке аргументов. Функция СЧЁТ используется для получения количества числовых ячеек в интервалах или массивах ячеек. • Синтаксис • СЧЁТ(значение 1; значение 2; . . . ) • Значение 1, значение 2, . . . — это от 1 до 30 аргументов, которые могут содержать или ссылаться на данные различных типов, но в подсчете участвуют только числа.

• Минимальное значение • МИН • Возвращает наименьшее значение в списке аргументов. • Синтаксис • МИН(число 1; число 2; . . . ) • Число 1, число 2, . . . — от 1 до 30 чисел, среди которых требуется найти наименьшее.

• Максимальное значение • МАКС • Возвращает наибольшее значение из набора значений. • Синтаксис • МАКС(число 1; число 2; . . . ) • Число 1, число 2, . . . — от 1 до 30 чисел, среди которых требуется найти наибольшее.

• Среднее арифметическое • СРЗНАЧ • Возвращает среднее (арифметическое) своих аргументов. • Синтаксис • СРЗНАЧ(число 1; число 2; . . . ) • Число 1, число 2, . . . — это от 1 до 30 аргументов, для которых вычисляется среднее.

• Среднее линейное отклонение • СРОТКЛ • Возвращает среднее абсолютных значений отклонений точек данных от среднего. СРОТКЛ является мерой разброса множества данных. • Синтаксис • СРОТКЛ(число 1; число 2; . . . ) • Число 1, число 2, . . . — это от 1 до 30 аргументов, для которых определяется среднее абсолютных отклонений. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

• Дисперсия по генеральной совокупности • • • ДИСПР Вычисляет дисперсию для генеральной совокупности. Синтаксис ДИСПР(число 1; число 2; . . . ) Число 1, число 2, . . . — от 1 до 30 числовых аргументов, соответствующих генеральной совокупности.

• Дисперсия (по выборке) • ДИСП Оценивает дисперсию по выборке. • Синтаксис • ДИСП(число 1; число 2; . . . ) • Число 1, число 2, . . . — от 1 до 30 числовых аргументов, соответствующих выборке из генеральной совокупности.

• Стандартное отклонение (среднеквадратическое отклонение) по генеральной совокупности • • СТАНДОТКЛОНП Вычисляет стандартное отклонение по генеральной совокупности. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего. Синтаксис СТАНДОТКЛОНП(число 1; число 2; . . . ) Число 1, число 2, . . . — от 1 до 30 числовых аргументов, соответствующих генеральной совокупности. Вместо аргументов, разделяемых точкой с запятой, также можно использовать массив или ссылку на массив. Текст и логические значения, такие как ИСТИНА или ЛОЖЬ игнорируются. Если текст и логические значения игнорироваться не должны, следует использовать функцию рабочего листа СТАНДОТКЛОНА. • •

• Стандартное отклонение (по выборке) • СТАНДОТКЛОН • Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего. • Синтаксис • СТАНДОТКЛОН(число 1; число 2; . . . ) • Число 1, число 2, . . . — от 1 до 30 числовых аргументов, соответствующих выборке из генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно также использовать массив или ссылку на массив.

• Коэффициент вариации

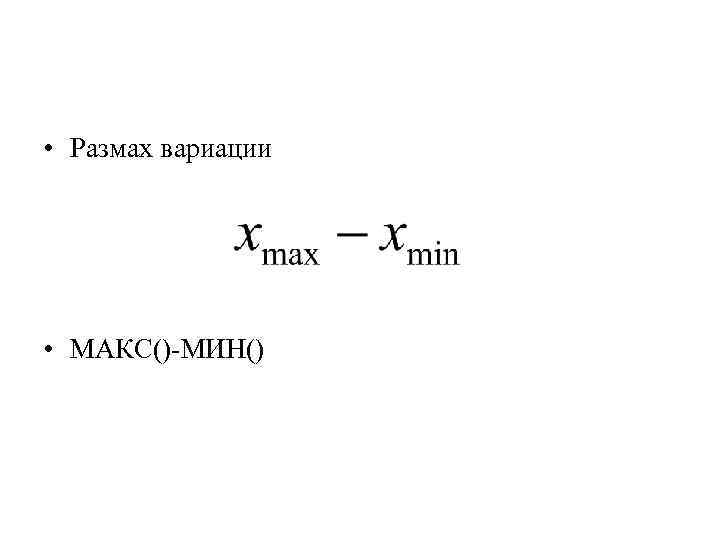• Размах вариации • МАКС()-МИН()

Построение ряда распределения • Ряд распределения содержит сгруппированные в интервалы наблюдения. В MS Excel есть функция ЧАСТОТА, которая избавляет исследователя от утомительной процедуры группировки данных по интервалам. Функция получает в качестве исходных данных диапазон с наблюдениями и границы интервалов. В качестве результата она возвращает частоты, т. е. число наблюдений, попавших в каждый интервал. Поскольку результатом функции является не одно значение, а целый набор, то эта функция отнесена к тем, которые работают с массивами данных. Перед записью таких функций нужно выделять диапазон, куда будет помещен результат, а ввод заканчивать нажатием клавиш Ctrl+Shift+Enter.

• ЧАСТОТА • Вычисляет частоту появления значений в интервале значений и возвращает массив цифр. Функция ЧАСТОТА может быть использована, например, для подсчета количества результатов тестирования, попадающих в интервалы результатов. Поскольку данная функция возвращает массив, она должна задаваться в качестве формулы массива. • Синтаксис • ЧАСТОТА(массив_данных; массив_интервалов) • Массив_данных — массив или ссылка на множество данных, для которых вычисляются частоты. Если массив_данных не содержит значений, то функция ЧАСТОТА возвращает массив нулей. • Массив_интервалов — массив или ссылка на множество интервалов, в которые группируются значения аргумента массив_данных. Если массив_интервалов не содержит значений, то функция ЧАСТОТА возвращает количество элементов в аргументе массив_данных.

Законы распределения случайных величин

• В MS Excel существуют функции, которые позволяют вычислить значения функции плотности распределения для большинства законов распределения вероятностей и функции, которые используются на различных этапах проверки гипотезы об определенном законе распределения.

• Нормальное распределение • НОРМРАСП • Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция имеет очень широкий круг приложений в статистике, включая проверку гипотез. • Синтаксис • НОРМРАСП(x; среднее; стандартное_откл; интегральна я) • x — значение, для которого строится распределение. • Среднее — среднее арифметическое распределения. • Стандартное_откл — стандартное отклонение распределения. • Интегральная — логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

• Стандартное нормальное • НОРМСТРАСП • Возвращает стандартное нормальное интегральное распределение. Это распределение имеет среднее, равное нулю, и стандартное отклонение, равное единице. Эта функция используется вместо таблицы для стандартной нормальной кривой. • Синтаксис • НОРМСТРАСП(z) • z — значение, для которого строится распределение.

• Логарифмическое стандартное • ЛОГНОРМРАСП • Возвращает интегральное логарифмическое нормальное распределение для x, где ln(x) является нормально распределенным с параметрами среднее и стандартное_откл. Эта функция используется для анализа данных, которые были логарифмически преобразованы. • Синтаксис • ЛОГНОРМРАСП(x; среднее; стандартное_откл) • x — значение, для которого вычисляется функция. • Среднее — среднее ln(x). • Стандартное_отклонение — стандартное отклонение ln(x).

• • • Биномиальное БИНОМРАСП Возвращает отдельное значение биномиального распределения. Функция БИНОМРАСП используется в задачах с фиксированным числом тестов или испытаний, когда результатом любого испытания может быть только успех или неудача, испытания независимы, и вероятность успеха постоянна на протяжении всего эксперимента. Например, БИНОМРАСП может вычислить вероятность того, что двое из трех следующих новорожденных будут мальчиками. Синтаксис БИНОМРАСП(число_успехов; число_испытаний; вероятность_успеха ; интегральная) Число_успехов — это количество успешных испытаний. Число_испытаний — это число независимых испытаний. Вероятность_успеха — это вероятность успеха каждого испытания. Интегральная — это логическое значение, определяющее форму функции. Если аргумент интегральная имеет значение ИСТИНА, то функция БИНОМРАСП возвращает интегральную функцию распределения, то есть вероятность того, что число успешных испытаний не менее значения аргумента число_успехов; если этот аргумент имеет значение ЛОЖЬ, то возвращается функция распределения, то есть вероятность того, что число успешных испытаний в точности равно значению аргумента число_успехов.

• Экспоненциальное • ЭКСПРАСП • Возвращает экспоненциальное распределение. Функция ЭКСПРАСП используется для моделирования временных задержек между событиями, например, сколько времени займет денежный перевод в автоматизированном банке. Функцию ЭКСПРАСП можно в частности использовать, чтобы определить вероятность того, что этот процесс займет не более 1 минуты. • Синтаксис • ЭКСПРАСП(x; лямбда ; интегральная) • x — это значение функции. • Лямбда — это значение параметра. • Интегральная — это логическое значение, которое указывает, какую форму экспоненциальной функции использовать. Если интегральная имеет значение ИСТИНА, то функция ЭКСПРАСП возвращает интегральную функцию распределения; если этот параметр имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

• Пуассона • ПУАССОН • Возвращает распределение Пуассона. Обычное применение распределения Пуассона состоит в предсказании количества событий, происходящих за определенное время, например, количество машин, появляющихся на площади за 1 минуту. • Синтаксис • ПУАССОН(x; среднее; интегральная) • x — количество событий. • Среднее — ожидаемое численное значение. • Интегральная — логическое значение, определяющее форму возвращаемого распределения вероятностей. Если аргумент «интегральная» имеет значение ИСТИНА, то функция ПУАССОН возвращает интегральное распределение Пуассона, то есть вероятность того, что число случайных событий будет от 0 до x включительно. Если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения Пуассона, то есть вероятность того, что событий будет в точности x.

• ХИ 2 ТЕСТ • Возвращает тест на независимость. ХИ 2 ТЕСТ возвращает значение для распределения хи-квадрат (χ2). Критерий χ2 используется для определения того, подтверждается ли гипотеза экспериментом. • Синтаксис • ХИ 2 ТЕСТ(фактический_интервал; ожидаемый_интерв ал) • Фактический_интервал — это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями. • Ожидаемый_интервал — это интервал данных, который содержит отношение произведений итогов по строкам и столбцам к общему итогу.

• ХИ 2 ОБР • Возвращает значение, обратное к односторонней вероятности распределения γ 2 (хи-квадрат). Если вероятность = ХИ 2 РАСП(x; . . . ), то ХИ 2 ОБР(вероятность; . . . ) = x. функция используется для сравнения наблюдаемых результатов с ожидаемыми, для того, чтобы решить была ли исходная гипотеза обоснованной. • Синтаксис • ХИ 2 ОБР(вероятность; степени_свободы) • Вероятность — это вероятность, связанная с распределением c 2 (хи-квадрат). • Степени_свободы — это число степеней свободы.

• ХИ 2 РАСП • Возвращает одностороннюю вероятность распределения хи-квадрат. Распределение χ2 связано с критерием χ2. Критерий χ2 используется для сравнения предполагаемых и наблюдаемых значений. Например, в генетическом эксперименте выдвигается гипотеза, что следующее поколение растений будет обладать определенной окраской. Сравнивая наблюдаемые результаты с предполагаемыми, можно определить, была ли исходная гипотеза обоснованной. • Синтаксис • ХИ 2 РАСП(x; степени_свободы) • x — это значение, для которого требуется вычислить распределение. • Степени_свободы — это число степеней свободы.