Статистические методы Регрессионный анализ Регрессионный анализ n

Статистические методы Регрессионный анализ

Регрессионный анализ n Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х 1, Х 2, … Хр и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). n Основная задача регрессионного состоит в выявлении связи между случайными переменными.

Различают два типа связей между различными явлениями и их признаками: n функциональную, или жестко детерминированную. Если § с изменением значения одной из переменных вторая изменяется строго определенным образом, т. е. значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной, связь между ними является функциональной. статистическую, или стохастически детерминированную. Если с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения с некоторыми вероятностями, но ее среднее значение или иные статистические (массовые) характеристики изменяются по определенному закону, связь является статистической.

Корреляционная связь n Корреляционной связью называют важнейший частный случай статистической связи, состоящий в том, что разным значениям одной переменной соответствуют различные средние значения другой. n С изменением значения признака х закономерным образом изменяется среднее значение признака у, в то время как в каждом отдельном случае значение признака у (с различными вероятностями) может принимать множество различных значений.

Условия применения корреляционно-регрессионного метода 1. 2. 3. Поскольку корреляционная связь является статистической, первым условием возможности ее изучения является наличие данных по достаточно большой совокупности. Обычно считают, что число наблюдений должно быть не менее чем в 5 — 6, а лучше — в 10 раз больше числа факторов. Еще лучше, если число наблюдений в несколько десятков или в сотни раз больше числа факторов, тогда закон больших чисел обеспечивает эффективное взаимопогашение случайных отклонений от закономерного характера связи признаков. Надежное выражение закономерности в средней величине. Кроме уже указанного большого числа единиц совокупности для этого необходима достаточная однородность совокупности В качестве третьего условия корреляционного анализа выдвигается необходимость подчинения распределения совокупности по результативному и факторным признакам нормальному закону распределения вероятностей. Это условие связано с применением метода наименьших квадратов при расчете параметров корреляции: только при нормальном распределении метод наименьших квадратов дает оценки параметров, отвечающих принципам максимального правдоподобия

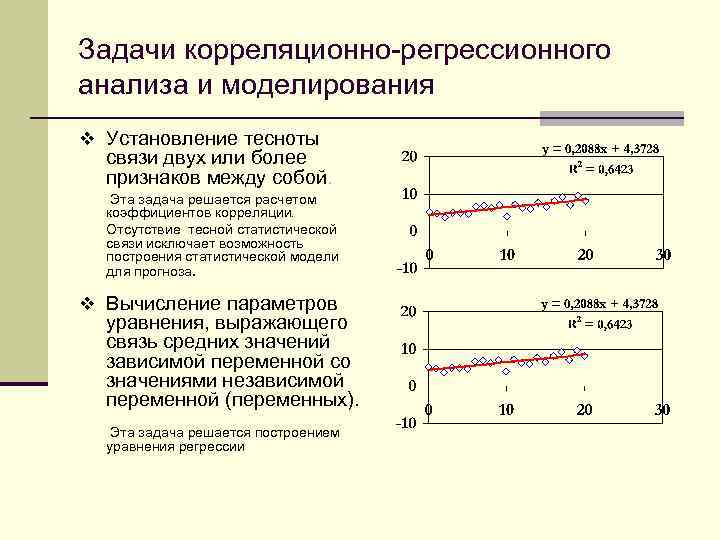Задачи корреляционно-регрессионного анализа и моделирования v Установление тесноты связи двух или более признаков между собой. Эта задача решается расчетом коэффициентов корреляции. Отсутствие тесной статистической связи исключает возможность построения статистической модели для прогноза. v Вычисление параметров уравнения, выражающего связь средних значений зависимой переменной со значениями независимой переменной (переменных). Эта задача решается построением уравнения регрессии

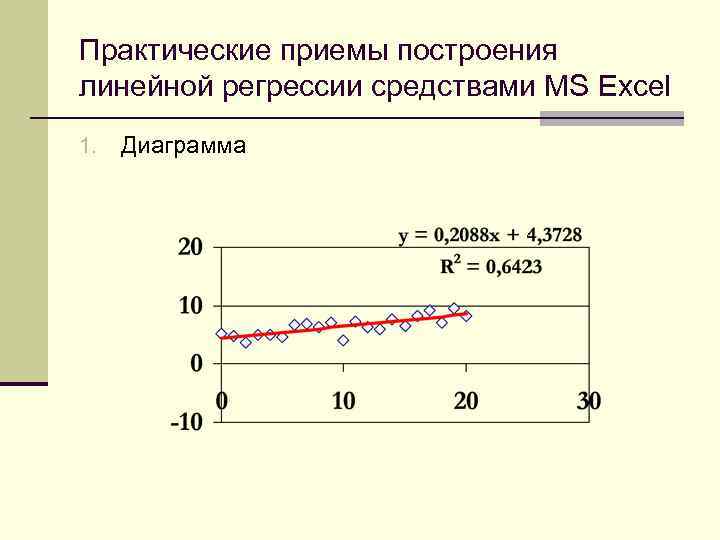Практические приемы построения линейной регрессии средствами MS Excel 1. Диаграмма

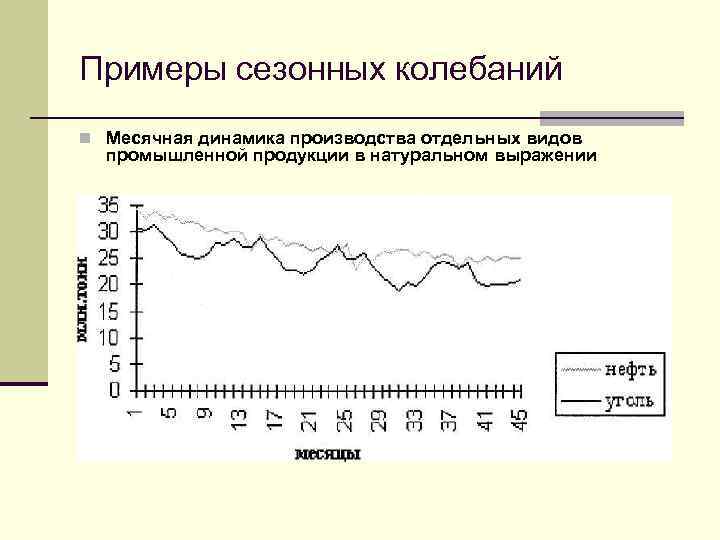Примеры сезонных колебаний n Месячная динамика производства отдельных видов промышленной продукции в натуральном выражении

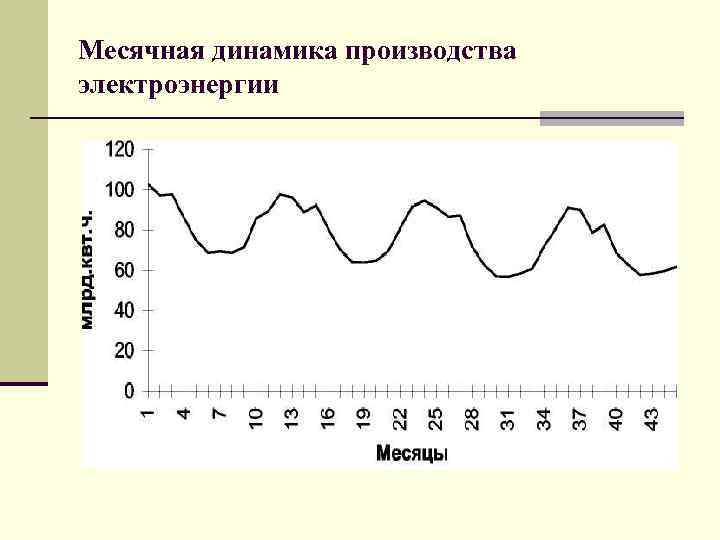Месячная динамика производства электроэнергии

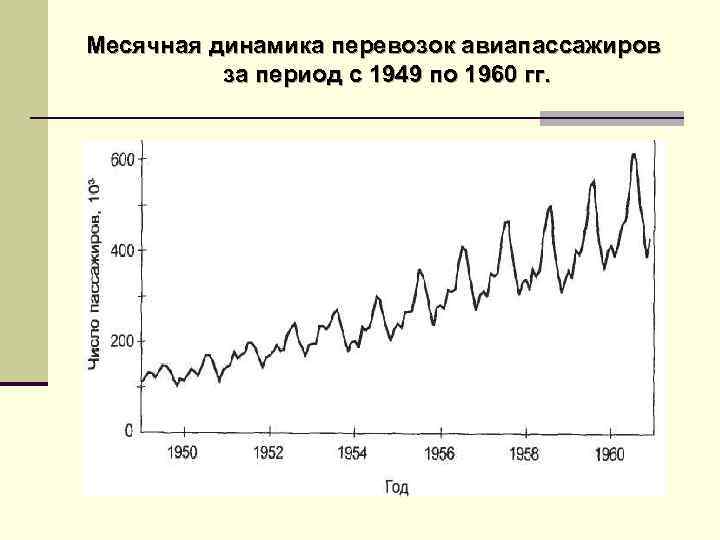Месячная динамика перевозок авиапассажиров за период с 1949 по 1960 гг.