Статистические критерии -2 ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ РАЗЛИЧИЯ Смысл

Статистические критерии -2

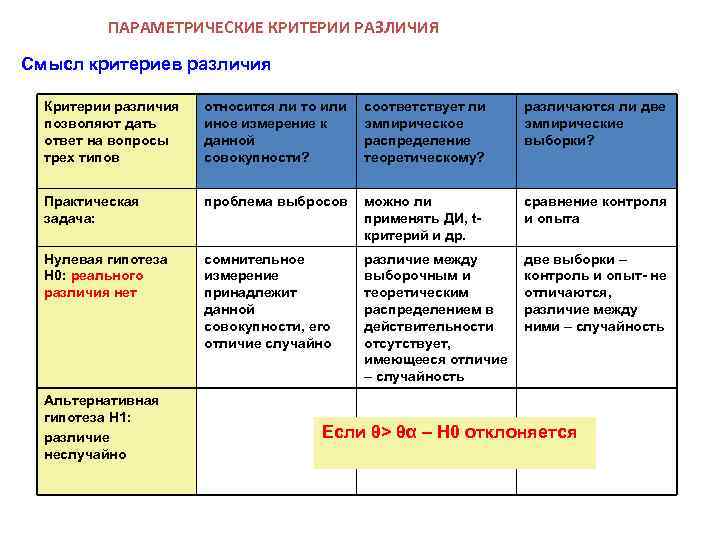ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ РАЗЛИЧИЯ Смысл критериев различия Критерии различия позволяют дать ответ на вопросы трех типов относится ли то или иное измерение к данной совокупности? соответствует ли эмпирическое распределение теоретическому? различаются ли две эмпирические выборки? Практическая задача: проблема выбросов можно ли применять ДИ, tкритерий и др. сравнение контроля и опыта Нулевая гипотеза Н 0: реального различия нет сомнительное измерение принадлежит данной совокупности, его отличие случайно различие между выборочным и теоретическим распределением в действительности отсутствует, имеющееся отличие – случайность две выборки – контроль и опыт- не отличаются, различие между ними – случайность Альтернативная гипотеза Н 1: различие неслучайно Если θ> θα – H 0 отклоняется

ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ РАЗЛИЧИЯ Принадлежность резко выделяющихся наблюдений к выборке x 1, x 2, …, xn-1, xn H 0: xn не является выбросом нулевая гипотеза статистика критерия 1. Правило четырех сигм (если n≥ 10) Если θ > 4 s - H 0 отклоняется 2. Критерий Диксона (если n ≤ 25) Если r > rα - H 0 отклоняется 3. Если n >25 Если t > tα - H 0 отклоняется условие проверки

ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ РАЗЛИЧИЯ 4 6 2 5 3 8 2 выборке Принадлежность резко выделяющихся наблюдений к 1 4 5 Является ли значение 8 выбросом? x , …, x 1 2 n-1 n N=10 H 0: xn не является выбросом 1. Правило четырех сигм (если n≥ 10) 1. θ=Ι 4 -8Ι=4 4 s=4*2. 11=8. 44 θ<4 s – H 0 не отклоняется, 8 – не выброс Если θ > 4 s - H 0 отклоняется 2. Критерий Диксона (если n ≤ 25) r 0, 05 = 0, 477 Если r > rα - H 0 отклоняется r < rα - H 0 не отклоняется, 8 – не выброс 3. Если n >25 Если t > tα - H 0 отклоняется t 0, 05 = 2. 11 t < tα , 8 – не выброс

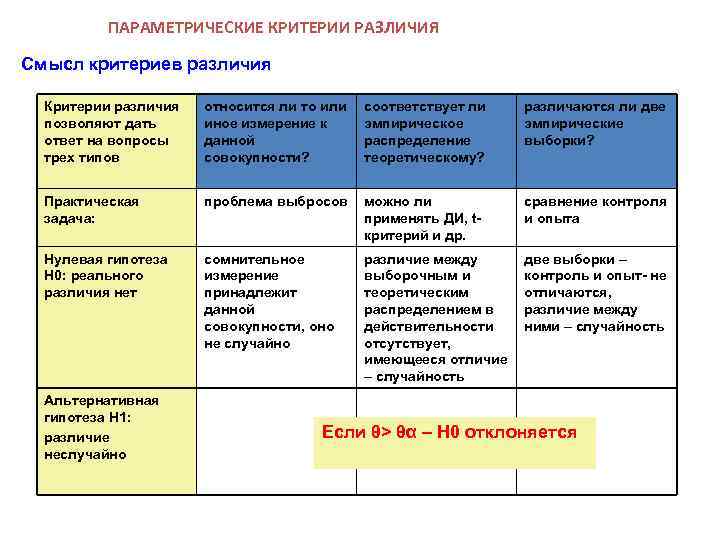ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ РАЗЛИЧИЯ Смысл критериев различия Критерии различия позволяют дать ответ на вопросы трех типов относится ли то или иное измерение к данной совокупности? соответствует ли эмпирическое распределение теоретическому? различаются ли две эмпирические выборки? Практическая задача: проблема выбросов можно ли применять ДИ, tкритерий и др. сравнение контроля и опыта Нулевая гипотеза Н 0: реального различия нет сомнительное измерение принадлежит данной совокупности, оно не случайно различие между выборочным и теоретическим распределением в действительности отсутствует, имеющееся отличие – случайность две выборки – контроль и опыт- не отличаются, различие между ними – случайность Альтернативная гипотеза Н 1: различие неслучайно Если θ> θα – H 0 отклоняется

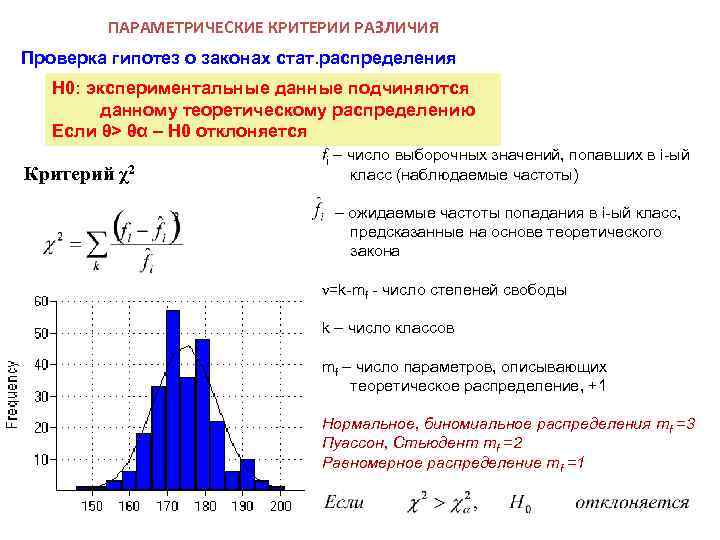ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ РАЗЛИЧИЯ Проверка гипотез о законах стат. распределения Н 0: экспериментальные данные подчиняются данному теоретическому распределению Если θ> θα – H 0 отклоняется Критерий χ2 fi – число выборочных значений, попавших в i-ый класс (наблюдаемые частоты) – ожидаемые частоты попадания в i-ый класс, предсказанные на основе теоретического закона ν=k-mf - число степеней свободы k – число классов mf – число параметров, описывающих теоретическое распределение, +1 Нормальное, биномиальное распределения mf =3 Пуассон, Стьюдент mf =2 Равномерное распределение mf =1

Объем выборки: Процедура не применима, если объем выборки (по разным рекомендациям) меньше 30 -50 n Практическая рекомендация для определения числа классов: k 40– 100– 500– 1000– 10000 7– 9 8– 12 10– 16 12– 22 .

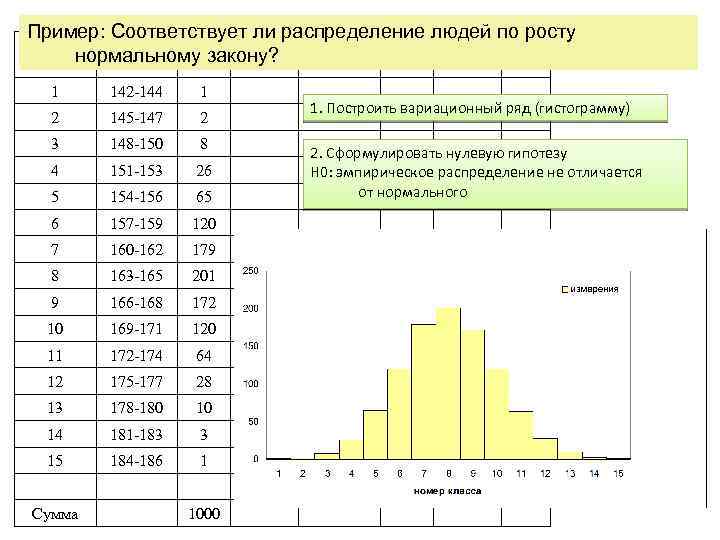Пример: Соответствует ли распределение людей по росту Номер Рост, см нормальномуfiзакону? класса i 1 142 -144 1 2 145 -147 2 3 148 -150 8 4 151 -153 26 5 154 -156 65 6 157 -159 120 7 160 -162 179 8 163 -165 201 9 166 -168 172 10 169 -171 120 11 172 -174 64 12 175 -177 28 13 178 -180 10 14 181 -183 3 15 184 -186 1 Сумма 1000 1. Построить вариационный ряд (гистограмму) 2. Сформулировать нулевую гипотезу H 0: эмпирическое распределение не отличается от нормального

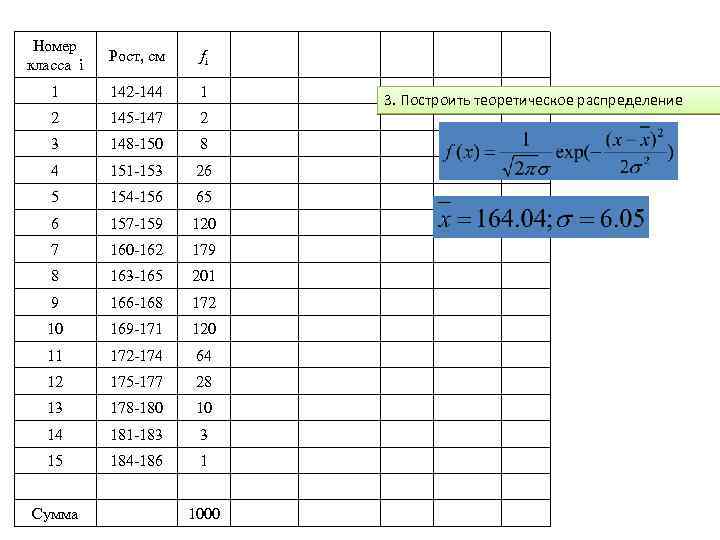Номер класса i Рост, см fi 1 142 -144 1 2 145 -147 2 3 148 -150 8 4 151 -153 26 5 154 -156 65 6 157 -159 120 7 160 -162 179 8 163 -165 201 9 166 -168 172 10 169 -171 120 11 172 -174 64 12 175 -177 28 13 178 -180 10 14 181 -183 3 15 184 -186 1 Сумма 1000 3. Построить теоретическое распределение

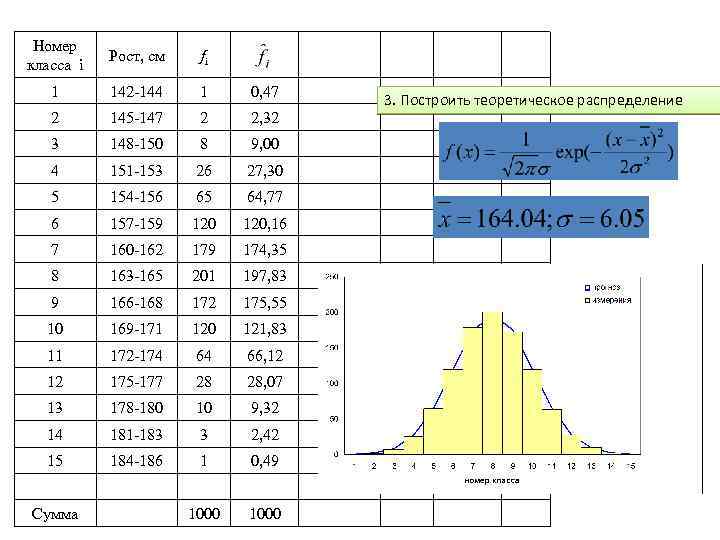Номер класса i Рост, см fi 1 142 -144 1 0, 47 2 145 -147 2 2, 32 3 148 -150 8 9, 00 4 151 -153 26 27, 30 5 154 -156 65 64, 77 6 157 -159 120, 16 7 160 -162 179 174, 35 8 163 -165 201 197, 83 9 166 -168 172 175, 55 10 169 -171 120 121, 83 11 172 -174 64 66, 12 12 175 -177 28 28, 07 13 178 -180 10 9, 32 14 181 -183 3 2, 42 15 184 -186 1 0, 49 1000 Сумма 3. Построить теоретическое распределение

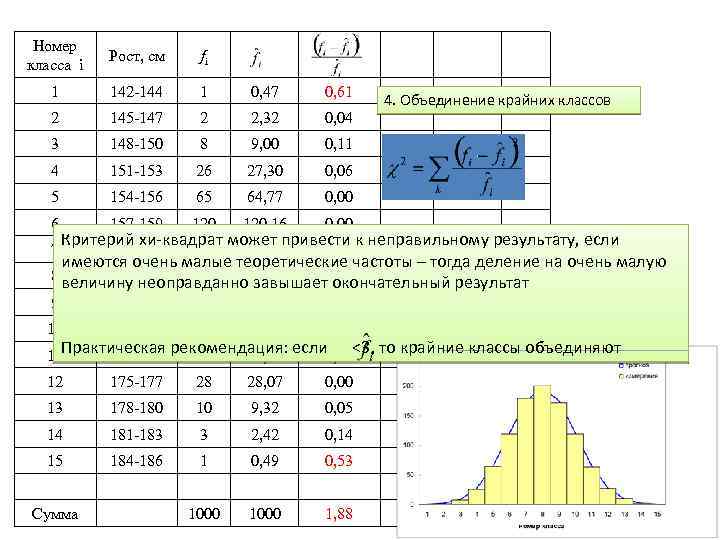Номер класса i Рост, см fi 1 142 -144 1 0, 47 0, 61 2 145 -147 2 2, 32 0, 04 3 148 -150 8 9, 00 0, 11 4 151 -153 26 27, 30 0, 06 5 154 -156 65 64, 77 0, 00 6 157 -159 120, 16 0, 00 9 166 -168 172 175, 55 0, 07 10 169 -171 120 121, 83 0, 03 12 175 -177 28 28, 07 0, 00 13 178 -180 10 9, 32 0, 05 14 181 -183 3 2, 42 0, 14 15 184 -186 1 0, 49 0, 53 1000 1, 88 4. Объединение крайних классов Критерий хи-квадрат может привести к неправильному результату, если 160 -162 179 174, 35 0, 12 имеются очень малые теоретические частоты – тогда деление на очень малую 8 величину неоправданно завышает0, 05 163 -165 201 197, 83 окончательный результат 7 11 Практическая рекомендация: если 0, 07<3, то крайние классы объединяют 172 -174 64 66, 12 Сумма

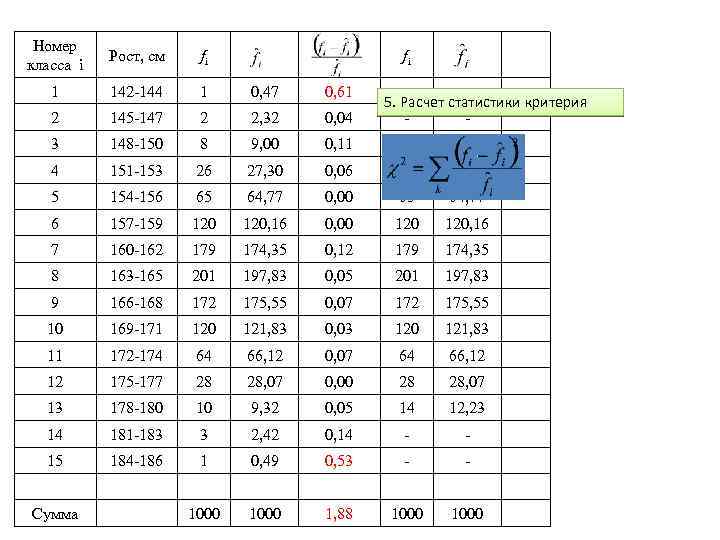Номер класса i Рост, см fi 1 142 -144 1 0, 47 0, 61 2 145 -147 2 2, 32 0, 04 3 148 -150 8 9, 00 0, 11 11 11, 79 4 151 -153 26 27, 30 0, 06 26 27, 30 5 154 -156 65 64, 77 0, 00 65 64, 77 6 157 -159 120, 16 0, 00 120, 16 7 160 -162 179 174, 35 0, 12 179 174, 35 8 163 -165 201 197, 83 0, 05 201 197, 83 9 166 -168 172 175, 55 0, 07 172 175, 55 10 169 -171 120 121, 83 0, 03 120 121, 83 11 172 -174 64 66, 12 0, 07 64 66, 12 12 175 -177 28 28, 07 0, 00 28 28, 07 13 178 -180 10 9, 32 0, 05 14 12, 23 14 181 -183 3 2, 42 0, 14 - - 15 184 -186 1 0, 49 0, 53 - - 1000 1, 88 1000 Сумма fi 5. Расчет статистики критерия -

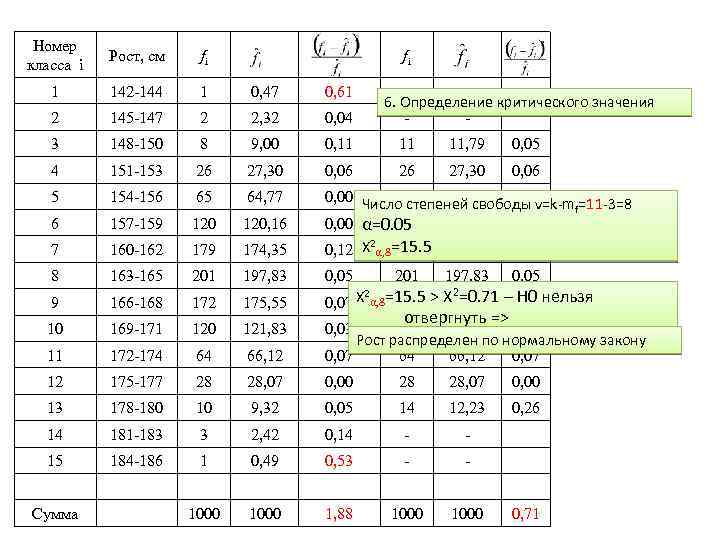Номер класса i Рост, см fi 1 142 -144 1 0, 47 0, 61 2 145 -147 2 2, 32 0, 04 3 148 -150 8 9, 00 0, 11 11 11, 79 0, 05 4 151 -153 26 27, 30 0, 06 5 154 -156 65 64, 77 6 157 -159 120, 16 7 160 -162 179 174, 35 0, 00 Число степеней свободы ν=k-m =11 -3=8 65 64, 77 0, 00 f 0, 00 α=0. 05 120, 16 0, 00 0, 12 Χ 2α, 8=15. 5 174, 35 0, 12 179 8 163 -165 201 197, 83 0, 05 9 166 -168 172 175, 55 0, 07 Χ 10 169 -171 120 121, 83 0, 03 11 172 -174 64 66, 12 120 121, 83 0, 03 Рост распределен по нормальному закону 0, 07 64 66, 12 0, 07 12 175 -177 28 28, 07 0, 00 13 178 -180 10 9, 32 0, 05 14 12, 23 0, 26 14 181 -183 3 2, 42 0, 14 - - 15 184 -186 1 0, 49 0, 53 - - 1000 1, 88 1000 Сумма fi 6. Определение критического значения - 201 2 α, 8=15. 5 172 197, 83 0, 05 > Χ 2=0. 71 – 0, 07 нельзя H 0 175, 55 отвергнуть => 0, 71

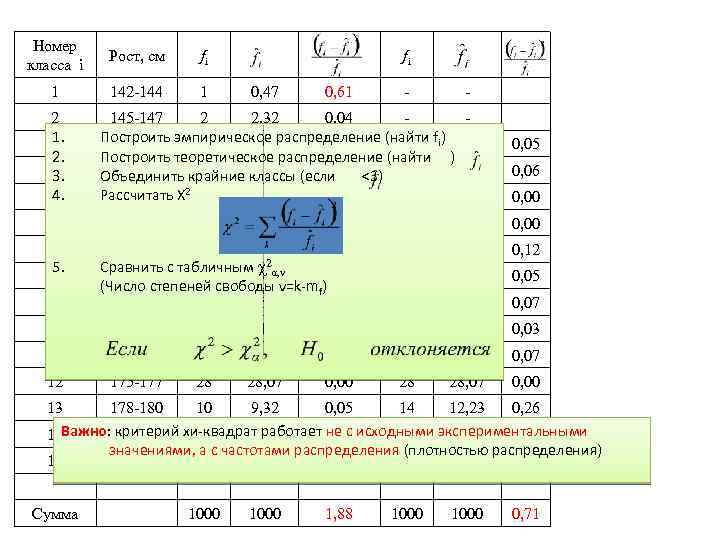Номер класса i Рост, см fi 1 142 -144 1 2 1. 3 2. 4 3. 4. 5 6 7 5. 8 9 fi 0, 47 0, 61 - - 145 -147 2 2, 32 0, 04 Построить эмпирическое распределение (найти fi) 11, 79 148 -150 8 9, 00 0, 11 11 Построить теоретическое распределение (найти ) 151 -153 26 0, 06 <3) 26 27, 30 Объединить крайние 27, 30 (если классы Рассчитать Χ 2 65 154 -156 64, 77 0, 00 65 64, 77 157 -159 120, 16 0, 05 0, 06 0, 00 120, 16 0, 00 160 -162 179 174, 35 0, 12 2 Сравнить с табличным χ α, v 163 -165 201 197, 83 0, 05 (Число степеней свободы ν=k-mf) 166 -168 172 175, 55 0, 07 179 174, 35 0, 12 201 197, 83 0, 05 172 175, 55 0, 07 10 169 -171 120 121, 83 0, 03 11 172 -174 64 66, 12 0, 07 12 175 -177 28 28, 07 0, 00 13 178 -180 10 9, 32 0, 05 14 12, 23 0, 26 критерий 3 не с 14 Важно: 181 -183 хи-квадрат работает 0, 14 исходными экспериментальными 2, 42 значениями, а с частотами распределения (плотностью распределения) 15 184 -186 1 0, 49 0, 53 Сумма 1000 1, 88 1000 0, 71

Задание Для проверки игральной кости было произведено 60 бросков. Наблюдаемые частоты появления каждого из 6 чисел следующие: 7 16 8 17 3 9. Проверить нуль-гипотезу – «кость идеальная» .

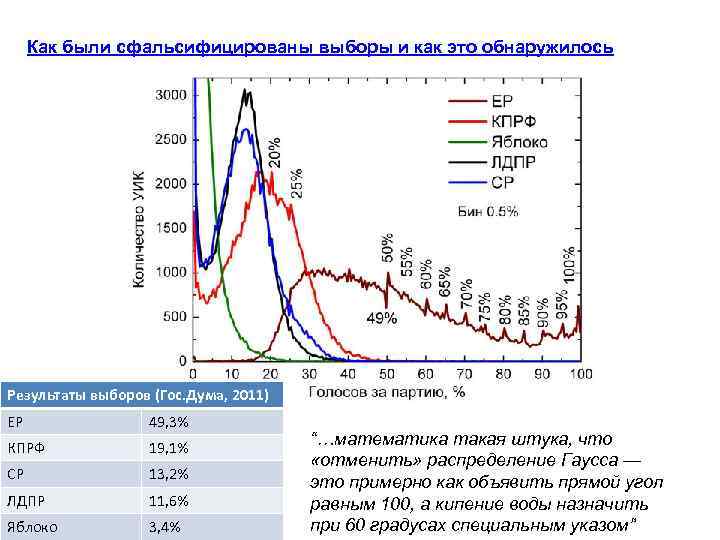Как были сфальсифицированы выборы и как это обнаружилось Результаты выборов (Гос. Дума, 2011) ЕР 49, 3% КПРФ 19, 1% СР 13, 2% ЛДПР 11, 6% Яблоко 3, 4% “…математика такая штука, что «отменить» распределение Гаусса — это примерно как объявить прямой угол равным 100, а кипение воды назначить при 60 градусах специальным указом”